Python을 사용한 AI –지도 학습 : 회귀
회귀는 가장 중요한 통계 및 기계 학습 도구 중 하나입니다. 기계 학습의 여정이 회귀에서 시작된다고 말하는 것은 잘못이 아닙니다. 데이터를 기반으로 결정을 내릴 수있는 매개 변수 기법으로 정의 할 수 있습니다. 즉, 입력 변수와 출력 변수 간의 관계를 학습하여 데이터를 기반으로 예측할 수 있습니다. 여기서 입력 변수에 종속 된 출력 변수는 연속 값 실수입니다. 회귀에서는 입력 변수와 출력 변수의 관계가 중요하며 입력 변수의 변화에 따라 출력 변수의 값이 어떻게 변하는 지 이해하는 데 도움이됩니다. 회귀는 가격, 경제, 변동 등을 예측하는 데 자주 사용됩니다.
Python에서 회귀 자 빌드
이 섹션에서는 단일 및 다중 변수 회귀자를 작성하는 방법을 배웁니다.
선형 회귀 / 단일 변수 회귀
몇 가지 필수 패키지를 중요하게하겠습니다.
import numpy as np
from sklearn import linear_model
import sklearn.metrics as sm
import matplotlib.pyplot as plt이제 입력 데이터를 제공해야하며 데이터를 linear.txt라는 파일에 저장했습니다.
input = 'D:/ProgramData/linear.txt'이 데이터를로드하려면 np.loadtxt 함수.
input_data = np.loadtxt(input, delimiter=',')
X, y = input_data[:, :-1], input_data[:, -1]다음 단계는 모델을 훈련시키는 것입니다. 교육 및 테스트 샘플을 제공하겠습니다.
training_samples = int(0.6 * len(X))
testing_samples = len(X) - num_training
X_train, y_train = X[:training_samples], y[:training_samples]
X_test, y_test = X[training_samples:], y[training_samples:]이제 선형 회귀 객체를 만들어야합니다.
reg_linear = linear_model.LinearRegression()훈련 샘플로 객체를 훈련시킵니다.
reg_linear.fit(X_train, y_train)테스트 데이터로 예측을해야합니다.
y_test_pred = reg_linear.predict(X_test)이제 데이터를 플로팅하고 시각화합니다.
plt.scatter(X_test, y_test, color = 'red')
plt.plot(X_test, y_test_pred, color = 'black', linewidth = 2)
plt.xticks(())
plt.yticks(())
plt.show()산출
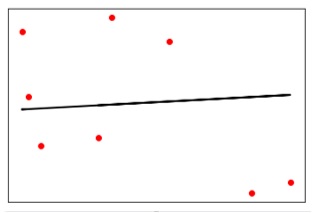
이제 다음과 같이 선형 회귀의 성능을 계산할 수 있습니다.
print("Performance of Linear regressor:")
print("Mean absolute error =", round(sm.mean_absolute_error(y_test, y_test_pred), 2))
print("Mean squared error =", round(sm.mean_squared_error(y_test, y_test_pred), 2))
print("Median absolute error =", round(sm.median_absolute_error(y_test, y_test_pred), 2))
print("Explain variance score =", round(sm.explained_variance_score(y_test, y_test_pred),
2))
print("R2 score =", round(sm.r2_score(y_test, y_test_pred), 2))산출
선형 회귀 분석기의 성능 −
Mean absolute error = 1.78
Mean squared error = 3.89
Median absolute error = 2.01
Explain variance score = -0.09
R2 score = -0.09위의 코드에서 우리는이 작은 데이터를 사용했습니다. 큰 데이터 세트를 원한다면 sklearn.dataset를 사용하여 더 큰 데이터 세트를 가져올 수 있습니다.
2,4.82.9,4.72.5,53.2,5.56,57.6,43.2,0.92.9,1.92.4,
3.50.5,3.41,40.9,5.91.2,2.583.2,5.65.1,1.54.5,
1.22.3,6.32.1,2.8다 변수 회귀 분석기
먼저 몇 가지 필수 패키지를 가져 오겠습니다.
import numpy as np
from sklearn import linear_model
import sklearn.metrics as sm
import matplotlib.pyplot as plt
from sklearn.preprocessing import PolynomialFeatures이제 입력 데이터를 제공해야하며 데이터를 linear.txt라는 파일에 저장했습니다.
input = 'D:/ProgramData/Mul_linear.txt'이 데이터는 np.loadtxt 함수.
input_data = np.loadtxt(input, delimiter=',')
X, y = input_data[:, :-1], input_data[:, -1]다음 단계는 모델을 훈련시키는 것입니다. 우리는 훈련 및 테스트 샘플을 제공 할 것입니다.
training_samples = int(0.6 * len(X))
testing_samples = len(X) - num_training
X_train, y_train = X[:training_samples], y[:training_samples]
X_test, y_test = X[training_samples:], y[training_samples:]이제 선형 회귀 객체를 만들어야합니다.
reg_linear_mul = linear_model.LinearRegression()훈련 샘플로 객체를 훈련시킵니다.
reg_linear_mul.fit(X_train, y_train)이제 드디어 테스트 데이터로 예측을해야합니다.
y_test_pred = reg_linear_mul.predict(X_test)
print("Performance of Linear regressor:")
print("Mean absolute error =", round(sm.mean_absolute_error(y_test, y_test_pred), 2))
print("Mean squared error =", round(sm.mean_squared_error(y_test, y_test_pred), 2))
print("Median absolute error =", round(sm.median_absolute_error(y_test, y_test_pred), 2))
print("Explain variance score =", round(sm.explained_variance_score(y_test, y_test_pred), 2))
print("R2 score =", round(sm.r2_score(y_test, y_test_pred), 2))산출
선형 회귀 분석기의 성능 −
Mean absolute error = 0.6
Mean squared error = 0.65
Median absolute error = 0.41
Explain variance score = 0.34
R2 score = 0.33이제 10 차 다항식을 만들고 회귀자를 훈련합니다. 샘플 데이터 포인트를 제공합니다.
polynomial = PolynomialFeatures(degree = 10)
X_train_transformed = polynomial.fit_transform(X_train)
datapoint = [[2.23, 1.35, 1.12]]
poly_datapoint = polynomial.fit_transform(datapoint)
poly_linear_model = linear_model.LinearRegression()
poly_linear_model.fit(X_train_transformed, y_train)
print("\nLinear regression:\n", reg_linear_mul.predict(datapoint))
print("\nPolynomial regression:\n", poly_linear_model.predict(poly_datapoint))산출
선형 회귀-
[2.40170462]다항 회귀-
[1.8697225]위의 코드에서 우리는이 작은 데이터를 사용했습니다. 큰 데이터 세트가 필요한 경우 sklearn.dataset를 사용하여 더 큰 데이터 세트를 가져올 수 있습니다.
2,4.8,1.2,3.22.9,4.7,1.5,3.62.5,5,2.8,23.2,5.5,3.5,2.16,5,
2,3.27.6,4,1.2,3.23.2,0.9,2.3,1.42.9,1.9,2.3,1.22.4,3.5,
2.8,3.60.5,3.4,1.8,2.91,4,3,2.50.9,5.9,5.6,0.81.2,2.58,
3.45,1.233.2,5.6,2,3.25.1,1.5,1.2,1.34.5,1.2,4.1,2.32.3,
6.3,2.5,3.22.1,2.8,1.2,3.6