Python을 사용한 AI-비지도 학습 : 클러스터링

비지도 머신 러닝 알고리즘에는 어떤 종류의 지침도 제공 할 감독자가 없습니다. 그렇기 때문에 그들은 일부 사람들이 진정한 인공 지능이라고 부르는 것과 밀접하게 연관되어 있습니다.

비지도 학습에서는 정답도없고지도를받을 교사도 없습니다. 알고리즘은 학습을 위해 데이터에서 흥미로운 패턴을 발견해야합니다.

클러스터링이란?

기본적으로 비지도 학습 방법의 한 유형이며 많은 분야에서 사용되는 통계 데이터 분석을위한 일반적인 기술입니다. 군집화는 주로 관측 값 집합을 군집이라고하는 하위 집합으로 나누는 작업으로, 동일한 군집의 관측치는 한 가지 의미에서 유사하고 다른 군집의 관측치와 유사하지 않습니다. 간단히 말해서, 클러스터링의 주요 목표는 유사성과 비 유사성을 기준으로 데이터를 그룹화하는 것입니다.

예를 들어, 다음 다이어그램은 서로 다른 클러스터에있는 유사한 종류의 데이터를 보여줍니다.

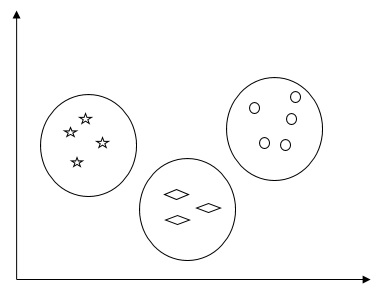
데이터 클러스터링을위한 알고리즘

다음은 데이터 클러스터링을위한 몇 가지 일반적인 알고리즘입니다.

K- 평균 알고리즘

K- 평균 클러스터링 알고리즘은 데이터를 클러스터링하기 위해 잘 알려진 알고리즘 중 하나입니다. 클러스터의 수가 이미 알려져 있다고 가정해야합니다. 이를 플랫 클러스터링이라고도합니다. 반복적 클러스터링 알고리즘입니다. 이 알고리즘을 위해서는 아래 단계를 따라야합니다.

Step 1 − 원하는 K 개의 부분 군 수를 지정해야합니다.

Step 2− 클러스터 수를 수정하고 각 데이터 포인트를 클러스터에 무작위로 할당합니다. 즉, 클러스터 수에 따라 데이터를 분류해야합니다.

이 단계에서는 군집 중심을 계산해야합니다.

이것은 반복 알고리즘이므로 글로벌 최적을 찾을 때까지, 즉 중심이 최적 위치에 도달 할 때까지 반복 할 때마다 K 중심의 위치를 ​​업데이트해야합니다.

다음 코드는 Python에서 K- 평균 클러스터링 알고리즘을 구현하는 데 도움이됩니다. Scikit-learn 모듈을 사용할 것입니다.

필요한 패키지를 가져 오겠습니다.

import matplotlib.pyplot as plt
import seaborn as sns; sns.set()
import numpy as np
from sklearn.cluster import KMeans

다음 코드 줄은 다음을 사용하여 4 개의 Blob을 포함하는 2 차원 데이터 세트를 생성하는 데 도움이됩니다. make_blob ~로부터 sklearn.dataset 꾸러미.

from sklearn.datasets.samples_generator import make_blobs

X, y_true = make_blobs(n_samples = 500, centers = 4,
            cluster_std = 0.40, random_state = 0)

다음 코드를 사용하여 데이터 세트를 시각화 할 수 있습니다.

plt.scatter(X[:, 0], X[:, 1], s = 50);
plt.show()

여기에서는 클러스터 수 (n_clusters)의 필수 매개 변수를 사용하여 KMeans 알고리즘이되도록 kmeans를 초기화합니다.

kmeans = KMeans(n_clusters = 4)

입력 데이터로 K- 평균 모델을 훈련해야합니다.

kmeans.fit(X)
y_kmeans = kmeans.predict(X)
plt.scatter(X[:, 0], X[:, 1], c = y_kmeans, s = 50, cmap = 'viridis')

centers = kmeans.cluster_centers_

아래에 제공된 코드는 데이터를 기반으로 한 기계의 결과와 발견 할 클러스터 수에 따른 피팅을 플롯하고 시각화하는 데 도움이됩니다.

plt.scatter(centers[:, 0], centers[:, 1], c = 'black', s = 200, alpha = 0.5);
plt.show()

평균 이동 알고리즘

비지도 학습에 사용되는 또 다른 인기 있고 강력한 클러스터링 알고리즘입니다. 어떤 가정도하지 않으므로 비모수 알고리즘입니다. 계층 적 군집화 또는 평균 이동 군집 분석이라고도합니다. 다음은이 알고리즘의 기본 단계입니다.

• 우선, 우리는 자체 클러스터에 할당 된 데이터 포인트로 시작해야합니다.

• 이제 중심을 계산하고 새 중심의 위치를 ​​업데이트합니다.

• 이 과정을 반복함으로써 우리는 클러스터의 피크, 즉 밀도가 높은 영역으로 더 가깝게 이동합니다.

• 이 알고리즘은 중심이 더 이상 움직이지 않는 단계에서 멈 춥니 다.

다음 코드의 도움으로 Python에서 Mean Shift 클러스터링 알고리즘을 구현하고 있습니다. Scikit-learn 모듈을 사용할 것입니다.

필요한 패키지를 가져 오겠습니다.

import numpy as np
from sklearn.cluster import MeanShift
import matplotlib.pyplot as plt
from matplotlib import style
style.use("ggplot")

다음 코드는 다음을 사용하여 4 개의 blob을 포함하는 2 차원 데이터 세트를 생성하는 데 도움이됩니다. make_blob ~로부터 sklearn.dataset 꾸러미.

from sklearn.datasets.samples_generator import make_blobs

다음 코드로 데이터 세트를 시각화 할 수 있습니다.

centers = [[2,2],[4,5],[3,10]]
X, _ = make_blobs(n_samples = 500, centers = centers, cluster_std = 1)
plt.scatter(X[:,0],X[:,1])
plt.show()

이제 입력 데이터를 사용하여 평균 이동 클러스터 모델을 훈련해야합니다.

ms = MeanShift()
ms.fit(X)
labels = ms.labels_
cluster_centers = ms.cluster_centers_

다음 코드는 입력 데이터에 따라 클러스터 센터와 예상 클러스터 수를 인쇄합니다.

print(cluster_centers)
n_clusters_ = len(np.unique(labels))
print("Estimated clusters:", n_clusters_)
[[ 3.23005036 3.84771893]
[ 3.02057451 9.88928991]]
Estimated clusters: 2

아래에 주어진 코드는 우리의 데이터를 기반으로 기계의 결과를 플롯하고 시각화하는 데 도움이되며 발견 될 클러스터 수에 따라 피팅을 시각화합니다.

colors = 10*['r.','g.','b.','c.','k.','y.','m.']
   for i in range(len(X)):
   plt.plot(X[i][0], X[i][1], colors[labels[i]], markersize = 10)
plt.scatter(cluster_centers[:,0],cluster_centers[:,1],
   marker = "x",color = 'k', s = 150, linewidths = 5, zorder = 10)
plt.show()

클러스터링 성능 측정

실제 데이터는 여러 개의 고유 한 클러스터로 자연스럽게 구성되지 않습니다. 이 때문에 추론을 시각화하고 도출하기가 쉽지 않습니다. 그렇기 때문에 클러스터링 성능과 품질을 측정해야합니다. 실루엣 분석의 도움으로 수행 할 수 있습니다.

실루엣 분석

이 방법은 클러스터 사이의 거리를 측정하여 클러스터링의 품질을 확인하는 데 사용할 수 있습니다. 기본적으로 실루엣 점수를 제공하여 군집 수와 같은 매개 변수를 평가하는 방법을 제공합니다. 이 점수는 한 클러스터의 각 포인트가 인접 클러스터의 포인트에 얼마나 가까운지를 측정하는 측정 항목입니다.

실루엣 점수 분석

점수의 범위는 [-1, 1]입니다. 다음은이 점수의 분석입니다-

• Score of +1 − +1에 가까운 점수는 샘플이 인접 클러스터에서 멀리 떨어져 있음을 나타냅니다.

• Score of 0 − 점수 0은 샘플이 인접한 두 군집 간의 결정 경계에 있거나 매우 가깝다는 것을 나타냅니다.

• Score of -1 − 음수 점수는 샘플이 잘못된 클러스터에 할당되었음을 나타냅니다.

실루엣 점수 계산

이 섹션에서는 실루엣 점수를 계산하는 방법을 배웁니다.

실루엣 점수는 다음 공식을 사용하여 계산할 수 있습니다.

$$ 실루엣 점수 = \ frac {\ left (pq \ right)} {max \ left (p, q \ right)} $$

여기서는 데이터 포인트가 속하지 않는 가장 가까운 군집의 포인트까지의 평균 거리입니다. 그리고는 자체 군집의 모든 점에 대한 평균 군집 내 거리입니다.

최적의 클러스터 수를 찾으려면 다음을 가져 와서 클러스터링 알고리즘을 다시 실행해야합니다. metrics 모듈에서 sklearn꾸러미. 다음 예에서는 최적의 클러스터 수를 찾기 위해 K- 평균 클러스터링 알고리즘을 실행합니다.

표시된대로 필요한 패키지를 가져옵니다.

import matplotlib.pyplot as plt
import seaborn as sns; sns.set()
import numpy as np
from sklearn.cluster import KMeans

다음 코드를 사용하여 4 개의 blob을 포함하는 2 차원 데이터 세트를 생성합니다. make_blob ~로부터 sklearn.dataset 꾸러미.

from sklearn.datasets.samples_generator import make_blobs

X, y_true = make_blobs(n_samples = 500, centers = 4, cluster_std = 0.40, random_state = 0)

다음과 같이 변수를 초기화하십시오.

scores = []
values = np.arange(2, 10)

모든 값을 통해 K- 평균 모델을 반복하고 입력 데이터로 훈련해야합니다.

for num_clusters in values:
kmeans = KMeans(init = 'k-means++', n_clusters = num_clusters, n_init = 10)
kmeans.fit(X)

이제 유클리드 거리 측정법을 사용하여 현재 클러스터링 모델의 실루엣 점수를 추정합니다.

score = metrics.silhouette_score(X, kmeans.labels_,
metric = 'euclidean', sample_size = len(X))

다음 코드 줄은 클러스터 수와 실루엣 점수를 표시하는 데 도움이됩니다.

print("\nNumber of clusters =", num_clusters)
print("Silhouette score =", score)
scores.append(score)

다음과 같은 출력을 받게됩니다.

Number of clusters = 9
Silhouette score = 0.340391138371

num_clusters = np.argmax(scores) + values[0]
print('\nOptimal number of clusters =', num_clusters)

이제 최적의 클러스터 수에 대한 출력은 다음과 같습니다.

Optimal number of clusters = 2

가장 가까운 이웃 찾기

영화 추천 시스템과 같은 추천 시스템을 구축하려면 가장 가까운 이웃을 찾는 개념을 이해해야합니다. 추천 시스템이 가장 가까운 이웃의 개념을 활용하기 때문입니다.

그만큼 concept of finding nearest neighbors주어진 데이터 셋에서 입력 포인트에 가장 가까운 포인트를 찾는 과정으로 정의 될 수 있습니다. 이 KNN) K- 최근 접 이웃) 알고리즘의 주요 용도는 다양한 클래스에 대한 입력 데이터 포인트의 근접성에 대한 데이터 포인트를 분류하는 분류 시스템을 구축하는 것입니다.

아래 주어진 Python 코드는 주어진 데이터 세트의 K- 최근 접 이웃을 찾는 데 도움이됩니다.

아래와 같이 필요한 패키지를 가져옵니다. 여기에서 우리는NearestNeighbors 모듈에서 sklearn 꾸러미

import numpy as np
import matplotlib.pyplot as plt
from sklearn.neighbors import NearestNeighbors

이제 입력 데이터를 정의하겠습니다.

A = np.array([[3.1, 2.3], [2.3, 4.2], [3.9, 3.5], [3.7, 6.4], [4.8, 1.9], 
             [8.3, 3.1], [5.2, 7.5], [4.8, 4.7], [3.5, 5.1], [4.4, 2.9],])

이제 가장 가까운 이웃을 정의해야합니다.

k = 3

또한 가장 가까운 이웃을 찾을 수있는 테스트 데이터를 제공해야합니다.

test_data = [3.3, 2.9]

다음 코드는 우리가 정의한 입력 데이터를 시각화하고 플로팅 할 수 있습니다.

plt.figure()
plt.title('Input data')
plt.scatter(A[:,0], A[:,1], marker = 'o', s = 100, color = 'black')

이제 K Nearest Neighbor를 구축해야합니다. 개체도 훈련해야합니다.

knn_model = NearestNeighbors(n_neighbors = k, algorithm = 'auto').fit(X)
distances, indices = knn_model.kneighbors([test_data])

이제 다음과 같이 K 개의 최근 접 이웃을 인쇄 할 수 있습니다.

print("\nK Nearest Neighbors:")
for rank, index in enumerate(indices[0][:k], start = 1):
   print(str(rank) + " is", A[index])

테스트 데이터 포인트와 함께 가장 가까운 이웃을 시각화 할 수 있습니다.

plt.figure()
plt.title('Nearest neighbors')
plt.scatter(A[:, 0], X[:, 1], marker = 'o', s = 100, color = 'k')
plt.scatter(A[indices][0][:][:, 0], A[indices][0][:][:, 1],
   marker = 'o', s = 250, color = 'k', facecolors = 'none')
plt.scatter(test_data[0], test_data[1],
   marker = 'x', s = 100, color = 'k')
plt.show()

산출

K Nearest Neighbors

1 is [ 3.1 2.3]
2 is [ 3.9 3.5]
3 is [ 4.4 2.9]

K-Nearest Neighbors 분류기

KNN (K-Nearest Neighbors) 분류기는 최근 접 이웃 알고리즘을 사용하여 주어진 데이터 포인트를 분류하는 분류 모델입니다. 마지막 섹션에서 KNN 알고리즘을 구현했습니다. 이제 해당 알고리즘을 사용하여 KNN 분류기를 구축 할 것입니다.

KNN 분류기의 개념

K- 최근 접 이웃 분류의 기본 개념은 분류되어야하는 새로운 샘플에 가장 가까운 훈련 샘플의 사전 정의 된 수, 즉 'k'를 찾는 것입니다. 새 샘플은 이웃 자체에서 라벨을받습니다. KNN 분류기는 결정해야하는 이웃 수에 대해 고정 된 사용자 정의 상수를 가지고 있습니다. 거리의 경우 표준 유클리드 거리가 가장 일반적인 선택입니다. KNN 분류기는 학습 규칙을 만드는 대신 학습 된 샘플에서 직접 작동합니다. KNN 알고리즘은 모든 기계 학습 알고리즘 중 가장 간단한 것입니다. 문자 인식 또는 이미지 분석과 같은 수많은 분류 및 회귀 문제에서 상당히 성공적이었습니다.

Example

우리는 숫자를 인식하기 위해 KNN 분류기를 만들고 있습니다. 이를 위해 MNIST 데이터 세트를 사용합니다. 이 코드를 Jupyter Notebook에 작성합니다.

아래와 같이 필요한 패키지를 가져옵니다.

여기서 우리는 KNeighborsClassifier 모듈에서 sklearn.neighbors 패키지 −

from sklearn.datasets import *
import pandas as pd
%matplotlib inline
from sklearn.neighbors import KNeighborsClassifier
import matplotlib.pyplot as plt
import numpy as np

다음 코드는 테스트해야 할 이미지를 확인하기 위해 숫자 이미지를 표시합니다.

def Image_display(i):
   plt.imshow(digit['images'][i],cmap = 'Greys_r')
   plt.show()

이제 MNIST 데이터 셋을로드해야합니다. 실제로 총 1797 개의 이미지가 있지만 처음 1600 개의 이미지를 학습 샘플로 사용하고 나머지 197 개는 테스트 목적으로 보관됩니다.

digit = load_digits()
digit_d = pd.DataFrame(digit['data'][0:1600])

이제 이미지를 표시 할 때 다음과 같이 출력을 볼 수 있습니다.

Image_display(0)

이미지 _ 디스플레이 (0)

0의 이미지는 다음과 같이 표시됩니다-

이미지 _ 디스플레이 (9)

9의 이미지는 다음과 같이 표시됩니다-

digit.keys ()

이제 훈련 및 테스트 데이터 세트를 생성하고 테스트 데이터 세트를 KNN 분류기에 제공해야합니다.

train_x = digit['data'][:1600]
train_y = digit['target'][:1600]
KNN = KNeighborsClassifier(20)
KNN.fit(train_x,train_y)

다음 출력은 K 가장 가까운 이웃 분류 자 ​​생성자를 생성합니다-

KNeighborsClassifier(algorithm = 'auto', leaf_size = 30, metric = 'minkowski',
   metric_params = None, n_jobs = 1, n_neighbors = 20, p = 2,
   weights = 'uniform')

훈련 샘플 인 1600보다 큰 임의의 숫자를 제공하여 테스트 샘플을 만들어야합니다.

test = np.array(digit['data'][1725])
test1 = test.reshape(1,-1)
Image_display(1725)

이미지 _ 디스플레이 (6)

6의 이미지는 다음과 같이 표시됩니다-

이제 다음과 같이 테스트 데이터를 예측합니다.

KNN.predict(test1)

위의 코드는 다음 출력을 생성합니다.

array([6])

이제 다음을 고려하십시오.

digit['target_names']

위의 코드는 다음 출력을 생성합니다.

array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])