인덕터의 회로 연결
인덕터는 회로에 연결될 때 직렬 또는 병렬로 연결될 수 있습니다. 이제 병렬로 연결될 때 직렬로 연결된 경우 총 전류, 전압 및 저항 값에 어떤 일이 발생하는지 알려주십시오.
직렬 인덕터
직렬로 연결된 인덕터가 거의 없을 때 어떤 일이 발생하는지 살펴 보겠습니다. 아래 그림과 같이 값이 다른 세 개의 저항을 고려해 보겠습니다.
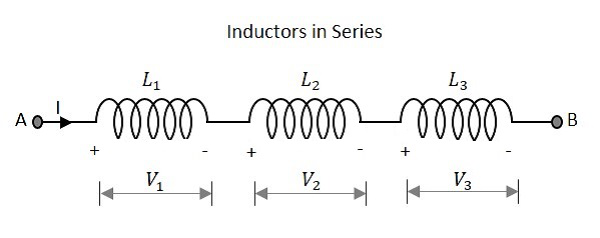
인덕턴스
직렬 인덕터가있는 회로의 총 인덕턴스는 개별 인덕턴스의 합과 같습니다. 위에 주어진 네트워크의 총 인덕턴스 값은
$$ L_ {T} \ : \ : = \ : \ : L_ {1} \ : \ : + \ : \ : L_ {2} \ : \ : + \ : \ : L_ {3} $$
여기서 L 1 은 첫 번째 저항 의 인덕턴스이고 , L 2 는 두 번째 저항 의 인덕턴스 이고 L 3 은 위의 네트워크에서 세 번째 저항 의 인덕턴스입니다 .
전압
직렬 인덕터 네트워크에 나타나는 총 전압은 각 개별 인덕턴스에서 전압 강하를 추가 한 것입니다.
회로에 나타나는 총 전압
$$ V \ : \ : = \ : \ : V_ {1} \ : \ : + \ : \ : V_ {2} \ : \ : + \ : \ : V_ {3} $$
여기서 V 1 은 첫 번째 인덕터 의 전압 강하 이고 V 2 는 두 번째 인덕터 의 전압 강하 이고 V 3 은 위의 네트워크에서 세 번째 인덕터 의 전압 강하 입니다.
흐름
직렬로 연결된 일련의 인덕터를 통해 흐르는 전류의 총량은 네트워크 전체의 모든 지점에서 동일합니다.
네트워크를 통한 전류
$$ I \ : \ : = \ : \ : I_ {1} \ : \ : = \ : \ : I_ {2} \ : \ : = \ : \ : I_ {3} $$
I 1 은 첫 번째 인덕터를 통과하는 전류 이고, I 2 는 두 번째 인덕터를 통과하는 전류 이고, I 3 은 위 네트워크에서 세 번째 인덕터를 통과하는 전류 입니다.
병렬 인덕터
병렬로 연결된 저항이 거의 없을 때 어떤 일이 발생하는지 살펴 보겠습니다. 아래 그림과 같이 값이 다른 세 개의 저항을 고려해 보겠습니다.

인덕턴스
병렬 저항이있는 회로의 총 인덕턴스는 직렬 인덕터 네트워크 방법과 다르게 계산됩니다. 여기에서 개별 인덕턴스의 역수 (1 / R) 값에 대수 합계의 역을 더하여 총 인덕턴스 값을 얻습니다.
네트워크의 총 인덕턴스 값은
$$ \ frac {1} {L_ {T}} \ : \ : = \ : \ : \ frac {1} {L_ {1}} \ : \ : + \ : \ : \ frac {1} {L_ { 2}} \ : \ : + \ : \ : \ frac {1} {L_ {3}} $$
여기서 L 1 은 첫 번째 인덕터 의 인덕턴스 이고 L 2 는 두 번째 인덕터 의 인덕턴스 이고 L 3 은 위 네트워크에서 세 번째 인덕터 의 인덕턴스입니다 .
병렬 인덕턴스를 계산하는 방법에서 두 인덕터 병렬 네트워크에 대한 간단한 방정식을 유도 할 수 있습니다. 그것은
$$ L_ {T} \ : \ : = \ : \ : \ frac {L_ {1} \ : \ : \ times \ : \ : L_ {2}} {L_ {1} \ : \ : + \ : \ : L_ {2}} $$
전압
병렬 인덕터 네트워크에 나타나는 총 전압은 각 개별 인덕턴스에서 전압 강하와 동일합니다.
회로에 나타나는 전압
$$ V \ : \ : = \ : \ : V_ {1} \ : \ : = \ : \ : V_ {2} \ : \ : = \ : \ : V_ {3} $$
여기서 V 1 은 첫 번째 인덕터 의 전압 강하 이고 V 2 는 두 번째 인덕터 의 전압 강하 이고 V 3 은 위의 네트워크에서 세 번째 인덕터 의 전압 강하 입니다. 따라서 전압은 병렬 인덕터 네트워크의 모든 지점에서 동일합니다.
흐름
병렬 유도 네트워크로 들어가는 총 전류량은 모든 병렬 분기에 흐르는 모든 개별 전류의 합입니다. 각 분기의 인덕턴스 값은 분기를 통해 흐르는 전류 값을 결정합니다.
네트워크를 통한 총 전류는
$$ I \ : \ : = \ : \ : I_ {1} \ : \ : + \ : \ : I_ {2} \ : \ : + \ : \ : I_ {3} $$
I 1 은 첫 번째 인덕터를 통과하는 전류 이고, I 2 는 두 번째 인덕터를 통과하는 전류 이고, I 3 은 위 네트워크에서 세 번째 인덕터를 통과하는 전류 입니다.
따라서 다른 분기의 개별 전류 합계는 병렬 네트워크의 총 전류를 얻습니다.
유도 성 리액턴스
유도 리액턴스는 인덕터가 교류 흐름 또는 단순히 AC 전류에 대해 제공하는 반대입니다. 인덕터는 전류 흐름의 변화에 저항하는 특성을 가지고 있으므로 다음과 같이 불릴 수있는 약간의 반대를 나타냅니다.reactance, 입력 전류의 주파수도 제공하는 저항과 함께 고려되어야합니다.
표시- XL
단위 − Ohms
기호 − Ω
순전히 유도 성 회로에서 전류 IL lags인가 전압을 90 °로합니다. 유도 리액턴스는 다음과 같이 계산됩니다.
$$ X_ {L} \ : \ : = \ : \ : 2 \ pi fL $$
여기서 f는 신호의 주파수입니다. 따라서 유도 리액턴스는 주파수와 인덕턴스의 함수입니다.