저항기의 회로 연결
회로에 연결된 경우 저항기는 직렬 또는 병렬이 될 수 있습니다. 이제 병렬로 연결될 때 직렬로 연결된 경우 총 전류, 전압 및 저항 값에 어떤 일이 발생하는지 알려주십시오.
직렬 저항기
직렬로 연결된 저항이 거의 없을 때 어떤 일이 발생하는지 살펴 보겠습니다. 아래 그림과 같이 값이 다른 세 개의 저항을 고려해 보겠습니다.
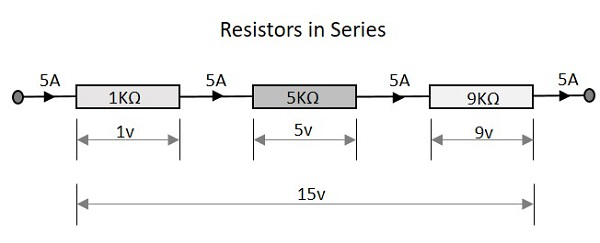
저항
직렬 저항이있는 회로의 총 저항은 개별 저항의 합과 같습니다. 즉, 위 그림에는 각각 1KΩ, 5KΩ 및 9KΩ 값을 갖는 세 개의 저항이 있습니다.
저항 네트워크의 총 저항 값은-
$$ R \ : \ : = \ : \ : R_ {1} \ : + \ : R_ {2} \ : + \ : R_ {3} $$
즉, 1 + 5 + 9 = 15KΩ이 총 저항입니다.
여기서 R 1 은 첫 번째 저항의 저항이고, R 2 는 두 번째 저항의 저항이고, R 3 은 위의 저항 네트워크에서 세 번째 저항의 저항입니다.
전압
직렬 저항 네트워크에 나타나는 총 전압은 각 개별 저항에서 전압 강하를 추가 한 것입니다. 위의 그림에서 우리는 각 단계에서 세 가지 전압 강하 값을 갖는 세 가지 다른 저항을 가지고 있습니다.
회로에 나타나는 총 전압-
$$ V \ : \ : = \ : \ : V_ {1} \ : + \ : V_ {2} \ : + \ : V_ {3} $$
즉, 1v + 5v + 9v = 15v가 총 전압입니다.
여기서 V 1 은 첫 번째 저항 의 전압 강하 이고 V 2 는 두 번째 저항 의 전압 강하 이고 V 3 은 위의 저항 네트워크에서 세 번째 저항 의 전압 강하입니다 .
흐름
직렬로 연결된 저항 세트를 통해 흐르는 전류의 총량은 저항 네트워크 전체의 모든 지점에서 동일합니다. 따라서 전류는 입력에서 측정하거나 저항기 사이 또는 출력에서 측정 할 때 동일한 5A입니다.
네트워크를 통한 전류-
$$ I \ : \ : = \ : \ : I_ {1} \ : = \ : I_ {2} \ : = \ : I_ {3} $$
이는 모든 지점의 전류가 5A임을 의미합니다.
I 1 은 첫 번째 저항을 통과하는 전류 이고, I 2 는 두 번째 저항을 통과하는 전류 이고, I 3 은 위의 저항 네트워크에서 세 번째 저항을 통과하는 전류 입니다.
병렬 저항
병렬로 연결된 저항이 거의 없을 때 어떤 일이 발생하는지 살펴 보겠습니다. 아래 그림과 같이 값이 다른 세 개의 저항을 고려해 보겠습니다.
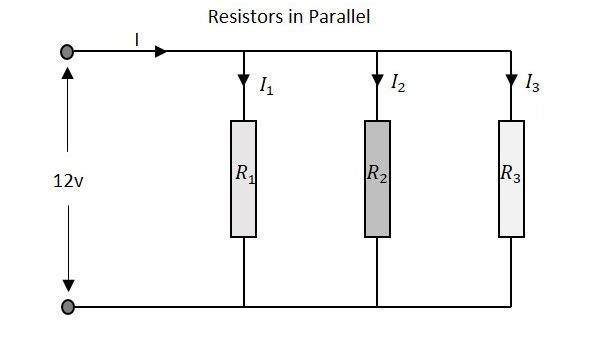
저항
병렬 저항이있는 회로의 총 저항은 직렬 저항 네트워크 방법과 다르게 계산됩니다. 여기에서 개별 저항의 역수 (1 / R) 값에 대수 합계의 역을 더하여 총 저항 값을 얻습니다.
저항 네트워크의 총 저항 값은-
$$ \ frac {1} {R} \ : \ : = \ : \ : \ frac {1} {R_ {1}} \ : \ : + \ : \ : \ frac {1} {R_ {2}} \ : \ : + \ frac {1} {R_ {3}} $$
여기서 R 1 은 첫 번째 저항의 저항이고, R 2 는 두 번째 저항의 저항이고, R 3 은 위의 저항 네트워크에서 세 번째 저항의 저항입니다.
예를 들어, 이전 예제의 저항 값을 고려하면 R 1 = 1KΩ, R 2 = 5KΩ 및 R 3 = 9KΩ을 의미합니다. 병렬 저항 네트워크의 총 저항은 다음과 같습니다.
$$ \ frac {1} {R} \ : \ : = \ : \ : \ frac {1} {1} \ : \ : + \ : \ : \ frac {1} {5} \ : \ : + \ frac {1} {9} $$
$$ = \ : \ : \ frac {45 \ : \ : + \ : \ : 9 \ : \ : + \ : \ : 5} {45} \ : \ : = \ : \ : \ frac {59} { 45} $$
$$ R \ : \ : = \ : \ : \ frac {45} {59} \ : \ : = \ : \ : 0.762K \ Omega \ : \ : = \ : \ : 76.2 \ Omega $$
병렬 저항을 계산하는 방법에서 2 저항 병렬 네트워크에 대한 간단한 방정식을 도출 할 수 있습니다. 그것은-
$$ R \ : \ : = \ : \ : \ frac {R_ {1} \ : \ : \ times \ : \ : R_ {2}} {R_ {1} \ : \ : + \ : \ : R_ { 2}} \ : $$
전압
병렬 저항 네트워크에 나타나는 총 전압은 각 개별 저항에서 전압 강하와 동일합니다.
회로에 나타나는 전압-
$$ V \ : \ : = \ : \ : V_ {1} \ : = \ : V_ {2} \ : = \ : V_ {3} $$
여기서 V 1 은 첫 번째 저항 의 전압 강하 이고 V 2 는 두 번째 저항 의 전압 강하 이고 V 3 은 위의 저항 네트워크에서 세 번째 저항 의 전압 강하입니다 . 따라서 전압은 병렬 저항 네트워크의 모든 지점에서 동일합니다.
흐름
병렬 저항 네트워크로 들어가는 전류의 총량은 모든 병렬 분기에 흐르는 모든 개별 전류의 합입니다. 각 분기의 저항 값은 분기를 통해 흐르는 전류의 값을 결정합니다. 네트워크를 통한 총 전류는
$$ I \ : \ : = \ : \ : I_ {1} \ : + \ : I_ {2} \ : + \ : I_ {3} $$
I 1 은 첫 번째 저항을 통과하는 전류 이고, I 2 는 두 번째 저항을 통과하는 전류 이고, I 3 은 위의 저항 네트워크에서 세 번째 저항을 통과하는 전류 입니다. 따라서 다른 분기에있는 개별 전류의 합은 병렬 저항 네트워크에서 총 전류를 얻습니다.
저항은 특히 많은 회로의 출력에서 부하로 사용됩니다. 저항 부하가 전혀 사용되지 않으면 저항이 부하 앞에 배치됩니다. 저항은 일반적으로 모든 회로의 기본 구성 요소입니다.