기본 전자-인덕턴스
전류 흐름의 변화에 의해 유도되는 전압을 얻기위한 인덕터의 특성을 인덕턴스로 정의합니다. 인덕턴스는 전류 변화율에 대한 전압의 비율입니다.
전류의 변화율은 자기장의 변화를 일으켜 전압원과 반대 방향으로 EMF를 유도합니다. EMF 유도의이 속성을Inductance.
인덕턴스의 공식은 다음과 같습니다.
$$ Inductance \ : \ : = \ : \ : \ frac {volatge} {rate \ : of \ : change \ : of \ : current} $$
Units −
인덕턴스의 단위는 Henry. 다음과 같이 표시됩니다.L.
인덕터는 대부분 mH (milli Henry) 및 μH (micro Henry)로 제공됩니다.
코일은 다음과 같은 인덕턴스를 가지고 있다고합니다. one Henry EMF가 one volt 전류가 흐르는 코일에서 자기 유도 one ampere per second.
자기 인덕턴스
일부 전류가 흐르는 코일을 고려하면 전류 흐름에 수직 인 자기장이 있습니다. 이 전류가 계속 변하면 자기장도 변하고이 변화하는 자기장은 소스 전압과 반대되는 EMF를 유도합니다. 생성 된이 반대 EMF는self-induced voltage 이 메서드는 다음과 같이 호출됩니다. self-inductance.
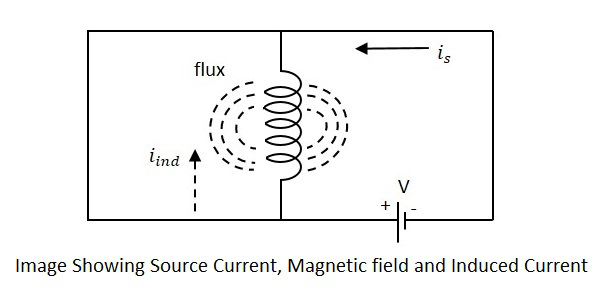
현재 is 그림에서 소스 전류를 나타내며 iind유도 전류를 나타냅니다. 플럭스는 코일 주위에 생성 된 자속을 나타냅니다. 전압을 가하면 전류가is흐름과 플럭스가 생성됩니다. 현재is 다양하고 플럭스는 다양해집니다. iind.
코일에 유도 된이 EMF는 전류의 변화율에 비례합니다. 전류의 변화율이 높을수록 유도되는 EMF 값이 높아집니다.
위의 방정식을 다음과 같이 쓸 수 있습니다.
$$ E \ : \ : \ alpha \ : \ : \ frac {dI} {dt} $$
$$ E \ : \ : = \ : \ : L \ : \ : \ frac {dI} {dt} $$
어디,
E 생산 된 EMF입니다
dI/dt 전류의 변화율을 나타냅니다.
L 인덕턴스 계수를 나타냅니다.
자기 인덕턴스 또는 자기 인덕턴스 계수는 다음과 같이 불릴 수 있습니다.
$$ L \ : \ : = \ : \ : \ frac {E} {\ frac {dI} {dt}} $$
실제 방정식은 다음과 같이 작성됩니다.
$$ E \ : \ : = \ : \ :-L \ : \ : \ frac {dI} {dt} $$
위 방정식의 마이너스는 the EMF is induced in opposite direction to the voltage source Lenz의 법칙에 따라.
상호 인덕턴스
전류 운반 코일이 주변에 약간의 자기장을 생성하기 때문에 다른 코일이이 코일 근처로 가져 와서 1 차측의 자속 영역에 있으면 다양한 자속이 두 번째 코일에서 EMF를 유도합니다. 이 첫 번째 코일이 다음과 같이 호출되면Primary coil, 두 번째는 Secondary coil.
1 차 코일의 자기장 변화에 의해 2 차 코일에서 EMF가 유도되면 이러한 현상을 Mutual Inductance.
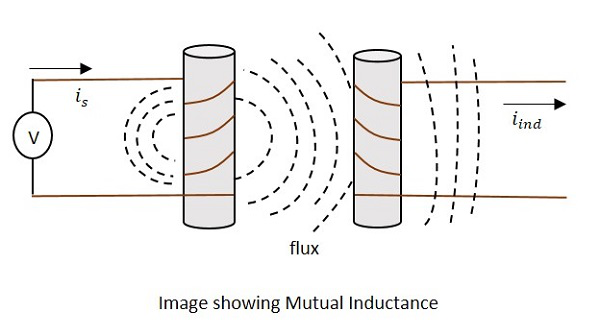
현재 is 그림에서 소스 전류를 나타내며 iind유도 전류를 나타냅니다. 플럭스는 코일 주위에 생성 된 자속을 나타냅니다. 이것은 또한 2 차 코일로 퍼집니다.
전압을 가하면 전류가 is흐름과 플럭스가 생성됩니다. 현재is 다양하고 플럭스는 다양해집니다. iind 상호 인덕턴스 속성으로 인해 2 차 코일에서.
이런 변화가 일어났습니다.
$$ V_ {p} \ : \ : I_ {p} \ rightarrow \ : \ : B \ : \ : \ rightarrow \ : \ : V_ {s} \ : \ : I_ {s} $$
어디,
Vp ip 1 차 코일의 전압과 전류를 각각 표시
B 자속을 나타냅니다.
Vs is 2 차 코일의 전압과 전류를 각각 표시
상호 인덕턴스 M 두 회로 중 1 차 전류의 변화에 의해 유도 된 2 차 전압의 양을 나타냅니다.
$$ V (보조) \ : \ : = \ : \ :-M \ frac {\ Delta I} {\ Delta t} $$
$ \ frac {\ Delta I} {\ Delta t} $ 시간에 따른 전류 변화율 M상호 인덕턴스의 계수입니다. 마이너스 기호는 소스와 반대되는 전류의 방향을 나타냅니다.
Units −
상호 인덕턴스의 단위는
$$ volt \ : \ : = \ : \ : M \ frac {amps} {sec} $$
(위 방정식에서)
$$ M \ : \ : = \ : \ : \ frac {volt. \ : sec} {amp} $$
$$ = \ : \ : 헨리 (H) $$
1 차 및 2 차 코일의 회전 수에 따라 자속 연결 및 유도 된 EMF의 양이 달라집니다. 1 차의 턴 수는 N1로 표시되고 2 차는 N2로 표시됩니다. 결합 계수는 두 코일의 상호 인덕턴스를 지정하는 용어입니다.
인덕턴스에 영향을 미치는 요인
인덕터의 성능에 영향을 미치는 몇 가지 요인이 있습니다. 주요 내용은 아래에서 설명합니다.
코일의 길이
인덕터 코일의 길이는 코일의 인덕턴스에 반비례합니다. 코일의 길이가 더 길면 해당 인덕터가 제공하는 인덕턴스가 줄어들고 그 반대의 경우도 마찬가지입니다.
코일의 단면적
코일의 단면적은 코일의 인덕턴스에 정비례합니다. 코일 면적이 클수록 인덕턴스가 높아집니다.
턴 수
권선 수에 따라 코일은 인덕턴스에 직접 영향을 미칩니다. 인덕턴스 값은 코일의 회전 수에 제곱됩니다. 따라서 권선 수가 많을수록 코일의 인덕턴스 값이 제곱됩니다.
코어의 투과성
그만큼 permeability (μ)인덕터의 코어 재료는 코어가 자체 내부에 자기장을 형성하기 위해 제공하는 지원을 나타냅니다. 그만큼higher 핵심 재료의 투자율, higher 인덕턴스가 될 것입니다.
결합 계수
이것은 두 코일의 상호 인덕턴스를 계산할 때 알아야 할 중요한 요소입니다. N1 및 N2 턴의 인접한 두 코일을 각각 고려해 보겠습니다.
첫 번째 코일 i 1을 통과하는 전류 는 일부 플럭스 Ψ 1을 생성합니다 . 자속 연결의 양은 weber-turns로 이해됩니다.
로 인해 I의 단위 전류와, 상기 제 2 코일을 쇄교 자속의 양을 보자 1 BE
$$ \ frac {N_ {2} \ varphi_ {1}} {i_ {1}} $$
이것은 상호 인덕턴스의 계수로 이해 될 수 있습니다.
$$ M \ : \ : = \ : \ : \ frac {N_ {2} \ varphi_ {1}} {i_ {1}} $$
따라서 두 코일 또는 회로 사이의 상호 인덕턴스 계수는 다른 코일의 1A 전류로 인해 한 코일에서 웨버 턴으로 이해됩니다.
첫 번째 코일의 자체 인덕턴스가 L 1 이면
$$ L_ {1} i_ {1} \ : \ : = \ : \ : {N_ {1} \ varphi_ {1}} \ : \ : => \ : \ : \ frac {L_ {1}} {N_ {1}} \ : \ : \ frac {\ varphi_ {1}} {i_ {1}} $$
$$ M \ : \ : = \ : \ : \ frac {N_ {2} L_ {1}} {N_ {1}} $$
마찬가지로, 두 번째 코일의 전류 i 2 로 인한 상호 인덕턴스 계수 는 다음과 같습니다.
$$ M \ : \ : = \ : \ : \ frac {N_ {1} \ varphi_ {2}} {i_ {2}} \ : \ dotsm \ : \ dotsm \ : \ dotsm \ : \ dotsm \ : \ : 1 $$
두 번째 코일의 자기 인덕턴스가 L 2 인 경우
$$ L_ {2} i_ {2} \ : \ : = \ : \ : N_ {2} \ varphi_ {2} $$
$$ \ frac {L_ {2}} {N_ {2}} \ : \ : = \ : \ : \ frac {\ varphi_ {2}} {i_ {2}} $$
따라서,
$$ M \ : \ : = \ : \ : \ frac {N_ {1} L_ {2}} {N_ {2}} \ : \ dotsm \ : \ dotsm \ : \ dotsm \ : \ dotsm \ : \ : 2 $$
1과 2를 곱하면
$$ M \ : \ : \ times \ : \ : M = \ : \ : \ frac {N_ {2} L_ {1}} {N_ {1}} \ : \ : \ times \ : \ : \ frac { N_ {1} L_ {2}} {N_ {2}} $$
$$ M ^ {2} \ : \ : = \ : \ : L_ {1} L_ {2} \ : \ : => \ : \ : M \ : \ : = \ : \ : \ sqrt {L_ {1 } L_ {2}} $$
위의 방정식은 1 차 코일의 전체 변화하는 플럭스가 2 차 코일과 연결될 때 사실이며 이는 이상적인 경우입니다. 그러나 실제로는 그렇지 않습니다. 따라서 다음과 같이 작성할 수 있습니다.
$$ M \ : \ : \ neq \ : \ : \ sqrt {L_ {1} L_ {2}} $$
$$ 및 \ frac {M} {\ sqrt {L_ {1} L_ {2}}} \ : \ : = \ : \ : K \ : \ : \ neq \ : \ : 1 $$
여기서 K는 결합 계수로 알려져 있습니다.
그만큼 Coefficient of coupling K 상호 인덕턴스의 이상적인 (최대) 계수에 대한 실제 상호 인덕턴스 계수의 비율로 정의 할 수 있습니다.
k의 값이 1에 가까우면 코일이 단단히 결합되었다고 말하고 k의 값이 0이면 코일이 느슨하게 결합되었다고합니다.
인덕터의 응용
다음과 같은 인덕터의 많은 응용 프로그램이 있습니다-
인덕터는 고주파 부품을 감지하고 노이즈 신호를 억제하기 위해 필터 회로에 사용됩니다.
원하지 않는 HF 신호로부터 회로를 분리합니다.
인덕터는 변압기를 형성하고 회로를 스파이크로부터 분리하기 위해 전기 회로에 사용됩니다.
인덕터는 모터에도 사용됩니다.