컴파일러 설계-유한 오토마타
유한 오토마타는 기호 문자열을 입력으로 받아 그에 따라 상태를 변경하는 상태 머신입니다. 유한 오토마타는 정규식 인식기입니다. 정규식 문자열이 유한 오토마타에 공급되면 각 리터럴에 대한 상태가 변경됩니다. 입력 문자열이 성공적으로 처리되고 자동 장치가 최종 상태에 도달하면 수락됩니다. 즉, 방금 공급 한 문자열이 현재 사용중인 언어의 유효한 토큰이라고합니다.
유한 오토마타의 수학적 모델은 다음으로 구성됩니다.
- 유한 상태 집합 (Q)
- 유한 입력 기호 집합 (Σ)
- One Start 상태 (q0)
- 최종 상태 세트 (qf)
- 전이 함수 (δ)
전이 함수 (δ)는 유한 상태 집합 (Q)을 유한 입력 기호 집합 (Σ), Q × Σ ➔ Q에 매핑합니다.
유한 오토마타 건설
L (r)을 유한 오토마타 (FA)에서 인식하는 정규 언어라고합시다.
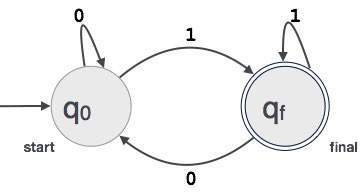
States: FA 상태는 원으로 표시됩니다. 주 이름은 원 안에 기록됩니다.
Start state: 오토마타가 시작되는 상태를 시작 상태라고합니다. 시작 상태에는 화살표가 있습니다.
Intermediate states: 모든 중간 상태에는 적어도 두 개의 화살표가 있습니다. 하나는 그들을 가리키고 다른 하나는 그들로부터 지적합니다.
Final state: 입력 문자열이 성공적으로 구문 분석되면 자동 장치는이 상태에있을 것으로 예상됩니다. 최종 상태는 이중 원으로 표시됩니다. 그것은 그것을 가리키는 임의의 홀수 개의 화살표와 그것을 가리키는 짝수의 화살표를 가질 수 있습니다. 홀수 화살표의 수는 짝수보다 하나 더 큽니다.odd = even+1.
Transition: 입력에서 원하는 기호가 발견되면 한 상태에서 다른 상태로의 전환이 발생합니다. 전환시 automata는 다음 상태로 이동하거나 동일한 상태를 유지할 수 있습니다. 한 상태에서 다른 상태로의 이동은 방향 화살표로 표시되며 화살표는 대상 상태를 가리 킵니다. automata가 같은 상태에 있으면 상태에서 자신을 가리키는 화살표가 그려집니다.
Example: FA는 숫자 1로 끝나는 3 자리 이진 값을 허용한다고 가정합니다. FA = {Q (q 0 , q f ), Σ (0,1), q 0 , q f , δ}