컴파일러 설계-퀵 가이드

컴퓨터는 소프트웨어와 하드웨어의 균형 잡힌 조합입니다. 하드웨어는 기계 장치의 일부일 뿐이며 해당 기능은 호환되는 소프트웨어에 의해 제어됩니다. 하드웨어는 소프트웨어 프로그래밍에서 이진 언어에 대응하는 전자 요금의 형태로 명령을 이해합니다. 이진 언어에는 0과 1이라는 두 개의 알파벳 만 있습니다. 지시하려면 하드웨어 코드는 단순히 일련의 1과 0 인 이진 형식으로 작성되어야합니다. 컴퓨터 프로그래머가 그러한 코드를 작성하는 것은 어렵고 번거로운 작업이 될 것입니다. 이것이 우리가 그러한 코드를 작성하는 컴파일러가있는 이유입니다.

언어 처리 시스템

우리는 모든 컴퓨터 시스템이 하드웨어와 소프트웨어로 구성된다는 것을 배웠습니다. 하드웨어는 인간이 이해할 수없는 언어를 이해합니다. 그래서 우리는 이해하고 기억하기 쉬운 고급 언어로 프로그램을 작성합니다. 그런 다음 이러한 프로그램은 일련의 도구 및 OS 구성 요소에 공급되어 기계에서 사용할 수있는 원하는 코드를 얻습니다. 이것은 언어 처리 시스템으로 알려져 있습니다.

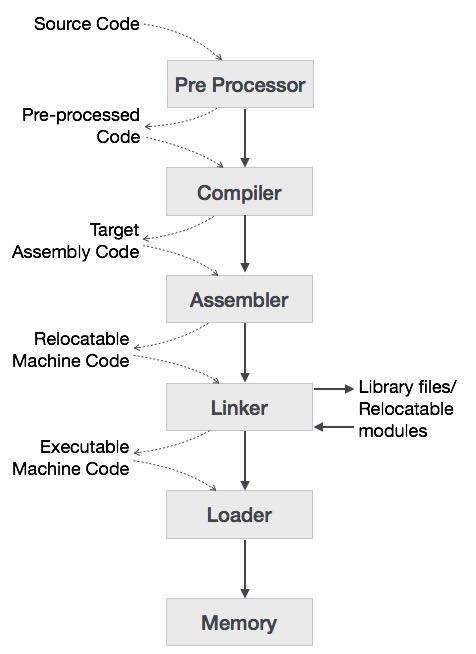
고급 언어는 다양한 단계에서 이진 언어로 변환됩니다. ㅏcompiler고급 언어를 어셈블리 언어로 변환하는 프로그램입니다. 마찬가지로assembler 어셈블리 언어를 기계 수준 언어로 변환하는 프로그램입니다.

먼저 C 컴파일러를 사용하는 프로그램이 호스트 시스템에서 실행되는 방식을 이해하겠습니다.

사용자가 C 언어 (고급 언어)로 프로그램을 작성합니다.
C 컴파일러는 프로그램을 컴파일하고이를 어셈블리 프로그램 (저수준 언어)으로 변환합니다.
그런 다음 어셈블러는 어셈블리 프로그램을 기계어 코드 (객체)로 변환합니다.
링커 도구는 실행을 위해 프로그램의 모든 부분을 함께 연결하는 데 사용됩니다 (실행 가능한 기계어 코드).
로더는 이들 모두를 메모리에로드 한 다음 프로그램이 실행됩니다.

컴파일러의 개념으로 바로 들어가기 전에 컴파일러와 밀접하게 작동하는 몇 가지 다른 도구를 이해해야합니다.

전 처리기

일반적으로 컴파일러의 일부로 간주되는 전처리 기는 컴파일러에 대한 입력을 생성하는 도구입니다. 매크로 처리, 증강, 파일 포함, 언어 확장 등을 다룹니다.

통역사

컴파일러와 같은 인터프리터는 높은 수준의 언어를 낮은 수준의 기계 언어로 번역합니다. 차이점은 소스 코드 또는 입력을 읽는 방식에 있습니다. 컴파일러는 한 번에 전체 소스 코드를 읽고, 토큰을 만들고, 의미를 확인하고, 중간 코드를 생성하고, 전체 프로그램을 실행하고, 여러 단계를 포함 할 수 있습니다. 반대로 인터프리터는 입력에서 명령문을 읽고 중간 코드로 변환하고 실행 한 다음 다음 명령문을 순서대로 가져옵니다. 오류가 발생하면 인터프리터는 실행을 중지하고이를보고합니다. 컴파일러는 여러 오류가 발생하더라도 전체 프로그램을 읽습니다.

어셈블러

어셈블러는 어셈블리 언어 프로그램을 기계어 코드로 변환합니다. 어셈블러의 출력을 개체 파일이라고하며 여기에는 기계 명령어와 이러한 명령어를 메모리에 배치하는 데 필요한 데이터의 조합이 포함됩니다.

링커

링커는 실행 파일을 만들기 위해 다양한 개체 파일을 함께 연결하고 병합하는 컴퓨터 프로그램입니다. 이러한 모든 파일은 별도의 어셈블러에 의해 컴파일되었을 수 있습니다. 링커의 주요 작업은 프로그램에서 참조 된 모듈 / 루틴을 검색하고 찾고 이러한 코드가로드 될 메모리 위치를 결정하여 프로그램 명령어가 절대 참조를 갖도록하는 것입니다.

짐을 싣는 사람

로더는 운영 체제의 일부이며 실행 파일을 메모리에로드하고 실행하는 역할을합니다. 프로그램의 크기 (명령 및 데이터)를 계산하고이를위한 메모리 공간을 생성합니다. 다양한 레지스터를 초기화하여 실행을 시작합니다.

크로스 컴파일러

플랫폼 (A)에서 실행되고 플랫폼 (B)에 대한 실행 코드를 생성 할 수있는 컴파일러를 크로스 컴파일러라고합니다.

소스-소스 컴파일러

한 프로그래밍 언어의 소스 코드를 가져 와서 다른 프로그래밍 언어의 소스 코드로 변환하는 컴파일러를 소스 간 컴파일러라고합니다.

컴파일러 아키텍처

컴파일러는 컴파일 방식에 따라 크게 두 단계로 나눌 수 있습니다.

분석 단계

컴파일러의 프런트 엔드로 알려진 analysis 컴파일러의 단계는 소스 프로그램을 읽고 핵심 부분으로 나눈 다음 어휘, 문법 및 구문 오류를 확인합니다. 분석 단계에서는 소스 프로그램과 기호 테이블의 중간 표현을 생성하여 입력으로 합성 단계에 공급해야합니다. .

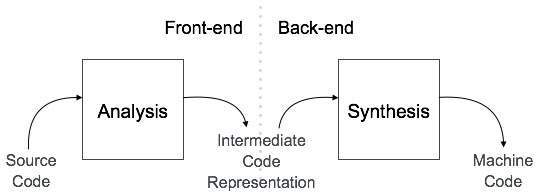
합성 단계

컴파일러의 백엔드로 알려진 synthesis 단계는 중간 소스 코드 표현 및 기호 테이블의 도움으로 대상 프로그램을 생성합니다.

컴파일러는 여러 단계와 패스를 가질 수 있습니다.

Pass : 패스는 전체 프로그램을 통한 컴파일러 순회를 나타냅니다.
Phase: 컴파일러의 단계는 구별 가능한 단계로, 이전 단계에서 입력을 받아 다음 단계의 입력으로 사용할 수있는 출력을 처리하고 산출합니다. 패스에는 여러 단계가있을 수 있습니다.

컴파일러 단계

컴파일 프로세스는 다양한 단계의 순서입니다. 각 단계는 이전 단계에서 입력을 받고 소스 프로그램의 자체 표현을 가지고 있으며 출력을 컴파일러의 다음 단계로 공급합니다. 컴파일러의 단계를 이해합시다.

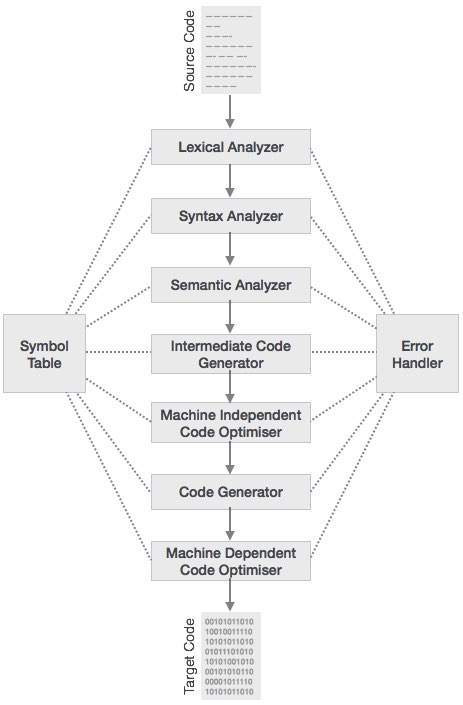
어휘 분석

스캐너의 첫 번째 단계는 텍스트 스캐너로 작동합니다. 이 단계에서는 소스 코드를 문자 스트림으로 스캔하여 의미있는 어휘로 변환합니다. 어휘 분석기는 다음과 같은 토큰 형태로 이러한 용어를 나타냅니다.

<token-name, attribute-value>

구문 분석

다음 단계는 구문 분석 또는 parsing. 어휘 분석에 의해 생성 된 토큰을 입력으로 사용하고 구문 분석 트리 (또는 구문 트리)를 생성합니다. 이 단계에서 토큰 배열은 소스 코드 문법에 대해 확인됩니다. 즉, 구문 분석기는 토큰에 의해 만들어진 표현이 구문 적으로 올바른지 확인합니다.

의미 분석

시맨틱 분석은 구성된 구문 분석 트리가 언어 규칙을 따르는 지 확인합니다. 예를 들어, 값 할당은 호환되는 데이터 유형간에 이루어지며 정수에 문자열을 추가합니다. 또한 시맨틱 분석기는 식별자, 유형 및 표현을 추적합니다. 식별자가 사용 전에 선언되었는지 여부 등. 의미 분석기는 주석이 달린 구문 트리를 출력으로 생성합니다.

중간 코드 생성

의미 론적 분석 후 컴파일러는 대상 머신에 대한 소스 코드의 중간 코드를 생성합니다. 추상적 인 기계를위한 프로그램을 나타냅니다. 고급 언어와 기계 언어 사이에 있습니다. 이 중간 코드는 대상 기계 코드로 쉽게 변환 할 수있는 방식으로 생성되어야합니다.

코드 최적화

다음 단계에서는 중간 코드의 코드 최적화를 수행합니다. 최적화는 불필요한 코드 줄을 제거하고 리소스 (CPU, 메모리)를 낭비하지 않고 프로그램 실행 속도를 높이기 위해 명령문 시퀀스를 정렬하는 것으로 간주 할 수 있습니다.

코드 생성

이 단계에서 코드 생성기는 중간 코드의 최적화 된 표현을 가져와 대상 기계 언어에 매핑합니다. 코드 생성기는 중간 코드를 (일반적으로) 재배치 가능한 일련의 기계 코드로 변환합니다. 일련의 기계어 코드는 중간 코드처럼 작업을 수행합니다.

기호 테이블

컴파일러의 모든 단계에서 유지되는 데이터 구조입니다. 유형과 함께 모든 식별자의 이름이 여기에 저장됩니다. 기호 테이블을 사용하면 컴파일러가 식별자 레코드를 빠르게 검색하고 검색 할 수 있습니다. 기호 테이블은 범위 관리에도 사용됩니다.

어휘 분석은 컴파일러의 첫 번째 단계입니다. 문장 형태로 작성된 언어 전 처리기에서 수정 된 소스 코드를 가져옵니다. 어휘 분석기는 소스 코드에서 공백이나 주석을 제거하여 이러한 구문을 일련의 토큰으로 나눕니다.

어휘 분석기가 유효하지 않은 토큰을 발견하면 오류를 생성합니다. 어휘 분석기는 구문 분석기와 밀접하게 작동합니다. 소스 코드에서 문자 스트림을 읽고, 합법적 인 토큰을 확인하고, 필요할 때 구문 분석기로 데이터를 전달합니다.

토큰

Lexemes는 토큰의 일련의 문자 (영숫자)라고합니다. 유효한 토큰으로 식별되는 모든 lexeme에 대해 미리 정의 된 규칙이 있습니다. 이러한 규칙은 패턴을 통해 문법 규칙에 의해 정의됩니다. 패턴은 토큰이 될 수있는 것을 설명하며 이러한 패턴은 정규식을 통해 정의됩니다.

프로그래밍 언어에서 키워드, 상수, 식별자, 문자열, 숫자, 연산자 및 구두점 기호는 토큰으로 간주 될 수 있습니다.

예를 들어, C 언어에서 변수 선언 줄

int value = 100;

다음 토큰을 포함합니다.

int (keyword), value (identifier), = (operator), 100 (constant) and ; (symbol).

토큰 사양

언어 이론이 다음 용어를 어떻게 수행하는지 이해합시다.

알파벳

유한 기호 집합 {0,1}은 이진 알파벳 집합 ({0,1,2,3,4,5,6,7,8,9, A, B, C, D, E, F})입니다. 16 진수 알파벳 집합, {az, AZ}는 영어 알파벳 집합입니다.

문자열

유한 한 알파벳 순서를 문자열이라고합니다. 문자열의 길이는 알파벳의 총 발생 횟수입니다. 예를 들어, tutorialspoint 문자열의 길이는 14이고 | tutorialspoint |로 표시됩니다. = 14. 알파벳이없는 문자열, 즉 길이가 0 인 문자열은 빈 문자열로 알려져 있으며 ε (엡실론)으로 표시됩니다.

특수 기호

일반적인 고급 언어에는 다음 기호가 포함됩니다.

산술 기호	더하기 (+), 빼기 (-), 모듈로 (%), 곱하기 (*), 나누기 (/)
구두	쉼표 (,), 세미콜론 (;), 점 (.), 화살표 (->)
할당	=
특별 과제	+ =, / =, * =,-=
비교	==,! =, <, <=,>,> =
전 처리기	#
위치 지정자	&
논리적	&, &&, \|, \|\|,!
시프트 연산자	>>, >>>, <<, <<<

언어

언어는 일부 유한 알파벳 세트에 대한 유한 문자열 세트로 간주됩니다. 컴퓨터 언어는 유한 집합으로 간주되며 수학적으로 설정된 연산을 수행 할 수 있습니다. 유한 언어는 정규식을 사용하여 설명 할 수 있습니다.

정규식

어휘 분석기는 사용중인 언어에 속하는 유한 한 유효한 문자열 / 토큰 / 어휘 집합 만 스캔하고 식별하면됩니다. 언어 규칙에 정의 된 패턴을 검색합니다.

정규식에는 유한 한 기호 문자열에 대한 패턴을 정의하여 유한 언어를 표현하는 기능이 있습니다. 정규식으로 정의 된 문법은 다음과 같습니다.regular grammar. 정규 문법으로 정의 된 언어는 다음과 같습니다.regular language.

정규식은 패턴을 지정하기위한 중요한 표기법입니다. 각 패턴은 문자열 세트와 일치하므로 정규 표현식은 문자열 세트의 이름 역할을합니다. 프로그래밍 언어 토큰은 일반 언어로 설명 할 수 있습니다. 정규식의 사양은 재귀 적 정의의 예입니다. 일반 언어는 이해하기 쉽고 효율적으로 구현됩니다.

정규 표현식이 따르는 대수 법칙이 많이 있으며, 정규 표현식을 동등한 형태로 조작하는 데 사용할 수 있습니다.

운영

언어에 대한 다양한 작업은 다음과 같습니다.

두 언어 L과 M의 결합은 다음과 같이 작성됩니다.

LUM = {s | s는 L 또는 s는 M}
두 언어 L과 M의 연결은 다음과 같이 작성됩니다.

LM = {st | s는 L, t는 M}
언어 L의 Kleene Closure는 다음과 같이 작성됩니다.

L * = 언어 L이 0 개 이상 발생합니다.

표기법

r과 s가 언어 L (r)과 L (s)을 나타내는 정규식이면

Union : (r) | (s)는 L (r) UL (s)을 나타내는 정규식입니다.
Concatenation : (r) (s)는 L (r) L (s)을 나타내는 정규식입니다.
Kleene closure : (r) *은 (L (r)) *을 나타내는 정규식입니다.
(r)은 L (r)을 나타내는 정규식입니다.

우선 순위 및 연관성

*, 연결 (.) 및 | (파이프 기호)는 연관되어 있습니다.
* 우선 순위가 가장 높습니다.
연결 (.)은 두 번째로 높은 우선 순위를 갖습니다.
| (파이프 기호)는 우선 순위가 가장 낮습니다.

정규식에서 언어의 유효한 토큰 표시

x가 정규식이면 다음과 같습니다.

x *는 x가 0 개 이상 발생 함을 의미합니다.

즉, {e, x, xx, xxx, xxxx,…}를 생성 할 수 있습니다.
x +는 하나 이상의 x 발생을 의미합니다.

즉, {x, xx, xxx, xxxx…} 또는 xx *를 생성 할 수 있습니다.
엑스? x의 최대 한 번 발생을 의미합니다.

즉, {x} 또는 {e}를 생성 할 수 있습니다.

[az]는 모두 영어의 소문자 알파벳입니다.

[AZ]는 모두 영어의 대문자 알파벳입니다.

[0-9]는 수학에서 사용되는 모든 자연 숫자입니다.

정규식을 사용하여 기호 발생 표시

letter = [a – z] 또는 [A – Z]

숫자 = 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 또는 [0-9]

기호 = [+ | -]

정규식을 사용하여 언어 토큰 표시

십진수 = (기호) ^?(숫자) ⁺

식별자 = (문자) (문자 | 숫자) *

어휘 분석기에 남은 유일한 문제는 언어의 키워드 패턴을 지정하는 데 사용되는 정규식의 유효성을 확인하는 방법입니다. 잘 받아 들여진 해결책은 검증을 위해 유한 오토마타를 사용하는 것입니다.

유한 오토마타

유한 오토마타는 기호 문자열을 입력으로 받아 그에 따라 상태를 변경하는 상태 머신입니다. 유한 오토마타는 정규식 인식기입니다. 정규식 문자열이 유한 오토마타에 공급되면 각 리터럴에 대한 상태가 변경됩니다. 입력 문자열이 성공적으로 처리되고 자동 장치가 최종 상태에 도달하면 수락됩니다. 즉, 방금 공급 한 문자열이 사용중인 언어의 유효한 토큰이라고합니다.

유한 오토마타의 수학적 모델은 다음으로 구성됩니다.

유한 상태 집합 (Q)
유한 입력 기호 집합 (Σ)
One Start 상태 (q0)
최종 상태 세트 (qf)
전이 함수 (δ)

전이 함수 (δ)는 유한 상태 집합 (Q)을 유한 입력 기호 집합 (Σ), Q × Σ ➔ Q에 매핑합니다.

유한 오토마타 건설

L (r)을 유한 오토마타 (FA)에서 인식하는 정규 언어라고합시다.

States: FA 상태는 원으로 표시됩니다. 주 이름은 원 안에 기록됩니다.
Start state: 오토마타가 시작되는 상태를 시작 상태라고합니다. 시작 상태에는 화살표가 있습니다.
Intermediate states: 모든 중간 상태에는 적어도 두 개의 화살표가 있습니다. 하나는 가리키고 다른 하나는 그들을 가리 킵니다.
Final state: 입력 문자열이 성공적으로 구문 분석되면 자동 장치는이 상태에있을 것으로 예상됩니다. 최종 상태는 이중 원으로 표시됩니다. 그것은 그것을 가리키는 임의의 홀수 개의 화살표와 그것을 가리키는 짝수의 화살표를 가질 수 있습니다. 홀수 화살표의 수는 짝수보다 하나 더 큽니다.odd = even+1.
Transition: 입력에서 원하는 기호가 발견되면 한 상태에서 다른 상태로의 전환이 발생합니다. 전환시 automata는 다음 상태로 이동하거나 동일한 상태를 유지할 수 있습니다. 한 상태에서 다른 상태로의 이동은 방향 화살표로 표시되며 화살표는 대상 상태를 가리 킵니다. automata가 같은 상태에 있으면 상태에서 자신을 가리키는 화살표가 그려집니다.

Example: FA는 숫자 1로 끝나는 3 자리 이진 값을 허용한다고 가정합니다. FA = {Q (q ₀ , q _f ), Σ (0,1), q ₀ , q _f , δ}

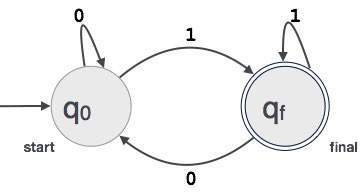
최장 일치 규칙

어휘 분석기가 소스 코드를 읽을 때 코드 문자를 문자별로 스캔합니다. 공백, 연산자 기호 또는 특수 기호를 만나면 단어가 완성 된 것으로 결정합니다.

For example:

int intvalue;

'int'까지 두 용어를 스캔하는 동안 어휘 분석기는 그것이 키워드 int 인지 식별자 int 값의 이니셜 인지 여부를 확인할 수 없습니다 .

가장 긴 일치 규칙은 사용 가능한 모든 토큰 중 가장 긴 일치를 기반으로 스캔 된 lexeme을 결정해야한다고 명시합니다.

어휘 분석기도 다음과 같습니다. rule priority여기서 언어의 예약어 (예 : 키워드)가 사용자 입력보다 우선합니다. 즉, 어휘 분석기가 기존 예약어와 일치하는 어휘를 찾으면 오류를 생성해야합니다.

구문 분석 또는 구문 분석은 컴파일러의 두 번째 단계입니다. 이 장에서는 파서 구성에 사용되는 기본 개념을 배웁니다.

어휘 분석기가 정규식 및 패턴 규칙을 사용하여 토큰을 식별 할 수 있음을 확인했습니다. 그러나 어휘 분석기는 정규 표현식의 한계로 인해 주어진 문장의 구문을 확인할 수 없습니다. 정규식은 괄호와 같은 균형 토큰을 확인할 수 없습니다. 따라서이 단계에서는 푸시 다운 자동 장치에서 인식하는 CFG (Context-free grammar)를 사용합니다.

반면 CFG는 아래와 같이 정규 문법의 상위 집합입니다.

그것은 모든 정규 문법도 문맥이 없다는 것을 의미하지만 정규 문법의 범위를 벗어난 몇 가지 문제가 있습니다. CFG는 프로그래밍 언어의 구문을 설명하는 데 유용한 도구입니다.

문맥 자유 문법

이 섹션에서는 먼저 문맥없는 문법의 정의를 살펴보고 구문 분석 기술에 사용되는 용어를 소개합니다.

문맥없는 문법에는 다음 네 가지 구성 요소가 있습니다.

세트 non-terminals(V). 비 터미널은 문자열 세트를 나타내는 구문 변수입니다. 비 터미널은 문법에 의해 생성 된 언어를 정의하는 데 도움이되는 문자열 세트를 정의합니다.
토큰 세트로 알려진 terminal symbols(Σ). 터미널은 문자열이 형성되는 기본 기호입니다.
세트 productions(피). 문법의 생성은 터미널과 비 터미널이 결합되어 문자열을 형성하는 방식을 지정합니다. 각 제작은non-terminal 생산의 왼쪽, 화살표, 일련의 토큰 및 / 또는 on- terminals, 생산의 오른쪽이라고합니다.
비 터미널 중 하나는 시작 기호 (S)로 지정됩니다. 생산이 시작되는 곳에서.

문자열은 비 터미널에 대해 프로덕션의 오른쪽으로 비 터미널 (처음에는 시작 기호)을 반복적으로 대체하여 시작 기호에서 파생됩니다.

예

우리는 정규 표현식으로 설명 할 수없는 회문 언어의 문제를 봅니다. 즉, L = {w | w = w ^R }은 일반 언어가 아닙니다. 그러나 아래 그림과 같이 CFG를 통해 설명 할 수 있습니다.

G = ( V, Σ, P, S )

어디:

V = { Q, Z, N }
Σ = { 0, 1 }
P = { Q → Z | Q → N | Q → ℇ | Z → 0Q0 | N → 1Q1 }
S = { Q }

이 문법은 1001, 11100111, 00100, 1010101, 11111 등과 같은 회문 언어를 설명합니다.

구문 분석기

구문 분석기 또는 구문 분석기는 토큰 스트림의 형태로 어휘 분석기에서 입력을받습니다. 파서는 프로덕션 규칙에 대해 소스 코드 (토큰 스트림)를 분석하여 코드의 오류를 감지합니다. 이 단계의 출력은parse tree.

이런 식으로 파서는 코드를 구문 분석하고 오류를 찾고 단계의 출력으로 구문 분석 트리를 생성하는 두 가지 작업을 수행합니다.

파서는 프로그램에 오류가 있어도 전체 코드를 구문 분석해야합니다. 파서는 오류 복구 전략을 사용하며이 장의 뒷부분에서 배울 것입니다.

유도

파생은 기본적으로 입력 문자열을 얻기위한 일련의 생산 규칙입니다. 파싱하는 동안 우리는 감각적 인 입력 형식에 대해 두 가지 결정을 내립니다.

교체 할 비 단말기 결정.
비 단말기를 대체 할 생산 규칙을 결정합니다.

생산 규칙으로 대체 할 비 터미널을 결정하기 위해 두 가지 옵션이 있습니다.

가장 왼쪽 파생

입력의 감각적 형태를 스캔하고 왼쪽에서 오른쪽으로 바꾸면이를 가장 왼쪽에서 파생이라고합니다. 가장 왼쪽에있는 파생물에 의해 파생 된 감각적 형식을 왼쪽 문장 형식이라고합니다.

가장 오른쪽 파생

입력을 스캔하고 오른쪽에서 왼쪽으로 프로덕션 규칙으로 바꾸면 가장 오른쪽 파생이라고합니다. 맨 오른쪽 파생에서 파생 된 감각 형식을 오른쪽 문장 형식이라고합니다.

Example

생산 규칙 :

E → E + E
E → E * E
E → id

입력 문자열 : id + id * id

가장 왼쪽의 파생은 다음과 같습니다.

E → E * E
E → E + E * E
E → id + E * E
E → id + id * E
E → id + id * id

가장 왼쪽에있는 비 터미널이 항상 먼저 처리됩니다.

가장 오른쪽 파생은 다음과 같습니다.

E → E + E
E → E + E * E
E → E + E * id
E → E + id * id
E → id + id * id

구문 분석 트리

구문 분석 트리는 파생을 그래픽으로 묘사 한 것입니다. 시작 기호에서 문자열이 어떻게 파생되는지 확인하는 것이 편리합니다. 파생의 시작 기호는 구문 분석 트리의 루트가됩니다. 마지막 주제의 예를 들어 보겠습니다.

우리는 a + b * c의 가장 왼쪽에있는 유도를 취합니다.

가장 왼쪽의 파생은 다음과 같습니다.

E → E * E
E → E + E * E
E → id + E * E
E → id + id * E
E → id + id * id

1 단계:

E → E * E

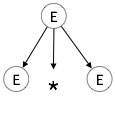
2 단계:

E → E + E * E

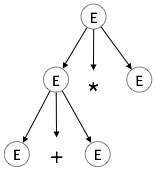
3 단계 :

E → id + E * E

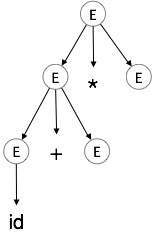
4 단계 :

E → id + id * E

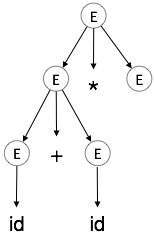
5 단계 :

E → id + id * id

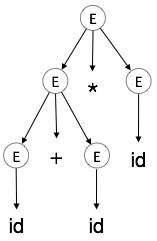
구문 분석 트리에서 :

모든 리프 노드는 터미널입니다.
모든 내부 노드는 비 터미널입니다.
순회 순회는 원래 입력 문자열을 제공합니다.

구문 분석 트리는 연산자의 연관성과 우선 순위를 나타냅니다. 가장 깊은 하위 트리가 먼저 탐색되므로 해당 하위 트리의 연산자가 상위 노드에있는 연산자보다 우선합니다.

구문 분석 유형

구문 분석기는 문맥없는 문법으로 정의 된 생산 규칙을 따릅니다. 생산 규칙이 구현 (파생)되는 방식은 파싱을 하향식 파싱과 상향식 파싱의 두 가지 유형으로 나눕니다.

하향식 구문 분석

파서가 시작 기호에서 구문 분석 트리를 구성하기 시작한 다음 시작 기호를 입력으로 변환하려고 할 때이를 하향식 구문 분석이라고합니다.

Recursive descent parsing: 하향식 구문 분석의 일반적인 형태입니다. 재귀 프로 시저를 사용하여 입력을 처리하므로 재귀라고합니다. 재귀 적 하강 파싱은 역 추적을 겪습니다.
Backtracking: 하나의 생산물 파생이 실패하면 구문 분석기가 동일한 생산의 다른 규칙을 사용하여 프로세스를 다시 시작 함을 의미합니다. 이 기술은 올바른 생산을 결정하기 위해 입력 문자열을 두 번 이상 처리 할 수 있습니다.

상향식 파싱

이름에서 알 수 있듯이 상향식 구문 분석은 입력 기호로 시작하여 시작 기호까지 구문 분석 트리를 구성하려고합니다.

Example:

입력 문자열 : a + b * c

생산 규칙 :

S → E
E → E + T
E → E * T
E → T
T → id

상향식 파싱을 시작하겠습니다.

a + b * c

입력을 읽고 생산이 입력과 일치하는지 확인하십시오.

a + b * c
T + b * c
E + b * c
E + T * c
E * c
E * T
E
S

모호

문법 G는 적어도 하나의 문자열에 대해 둘 이상의 구문 분석 트리 (왼쪽 또는 오른쪽 파생)가있는 경우 모호하다고합니다.

Example

E → E + E
E → E – E
E → id

문자열 id + id – id의 경우 위의 문법은 두 개의 구문 분석 트리를 생성합니다.

모호한 문법에 의해 생성 된 언어는 inherently ambiguous. 문법의 모호성은 컴파일러 구성에 좋지 않습니다. 어떤 방법도 모호성을 자동으로 감지하고 제거 할 수는 없지만 모호함없이 전체 문법을 다시 작성하거나 연관성 및 우선 순위 제약 조건을 설정하고 따르는 방법으로 제거 할 수 있습니다.

연관성

피연산자의 양쪽에 연산자가있는 경우 연산자가이 피연산자를 취하는 쪽은 해당 연산자의 연관성에 의해 결정됩니다. 연산이 왼쪽 연관이면 피연산자는 왼쪽 연산자가 취하고 연산이 오른쪽 연관이면 오른쪽 연산자는 피연산자를 취합니다.

Example

더하기, 곱하기, 빼기 및 나눗셈과 같은 연산은 연관되어 있습니다. 표현식에 다음이 포함 된 경우 :

id op id op id

다음과 같이 평가됩니다.

(id op id) op id

예 : (id + id) + id

Exponentiation과 같은 연산은 올바른 연관성입니다. 즉, 동일한 표현식의 평가 순서는 다음과 같습니다.

id op (id op id)

예 : id ^ (id ^ id)

상위

두 개의 다른 연산자가 공통 피연산자를 공유하는 경우 연산자의 우선 순위에 따라 어떤 연산자가 피연산자를 사용할지 결정됩니다. 즉, 2 + 3 * 4는 (2 + 3) * 4에 해당하는 것과 2+ (3 * 4)에 해당하는 두 개의 다른 구문 분석 트리를 가질 수 있습니다. 오퍼레이터 간의 우선 순위를 설정함으로써이 문제를 쉽게 제거 할 수 있습니다. 이전 예에서와 같이 수학적으로 * (곱하기)는 + (더하기)보다 우선하므로 표현식 2 + 3 * 4는 항상 다음과 같이 해석됩니다.

2 + (3 * 4)

이러한 방법은 언어 또는 문법의 모호성 가능성을 줄입니다.

왼쪽 재귀

파생에 'A'자체가 맨 왼쪽 기호로 포함 된 비 말단 'A'가있는 경우 문법은 왼쪽 재귀 적이됩니다. 왼쪽 재귀 문법은 하향식 파서에게 문제가되는 상황으로 간주됩니다. 하향식 구문 분석기는 그 자체가 터미널이 아닌 시작 기호에서 구문 분석을 시작합니다. 따라서 파서가 파생에서 동일한 비 터미널을 만나면 왼쪽 비 터미널 구문 분석을 중지해야 할 때를 판단하기가 어려워지고 무한 루프에 들어갑니다.

Example:

(1) A => Aα | β

(2) S => Aα | β 
    A => Sd

(1)은 즉시 왼쪽 재귀의 예입니다. 여기서 A는 비 터미널 기호이고 α는 비 터미널 문자열을 나타냅니다.

(2)는 간접 좌회전 재귀의 예입니다.

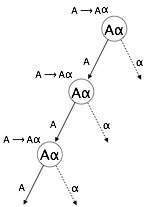
하향식 파서는 먼저 A를 파싱합니다. 그러면 A 자체로 구성된 문자열이 생성되고 파서는 영원히 루프에 들어갈 수 있습니다.

왼쪽 재귀 제거

왼쪽 재귀를 제거하는 한 가지 방법은 다음 기술을 사용하는 것입니다.

생산

A => Aα | β

다음 작품으로 전환

A => βA’
A => αA’ | ε

이것은 문법에서 파생 된 문자열에 영향을주지 않지만 즉시 왼쪽 재귀를 제거합니다.

두 번째 방법은 다음 알고리즘을 사용하는 것입니다.이 알고리즘은 모든 직접 및 간접 왼쪽 재귀를 제거합니다.

Algorithm
START
Arrange non-terminals in some order like A1, A2, A3,…, An
for each i from 1 to n
{
for each j from 1 to i-1
   {
   replace each production of form Ai⟹Aj
   with Ai ⟹ δ1  | δ2 | δ3 |…|  
   where Aj ⟹ δ1 | δ2|…| δn  are current Aj productions
}
   }
   eliminate immediate left-recursion
END

Example

생산 세트

S => Aα | β 
A => Sd

위의 알고리즘을 적용한 후

S => Aα | β 
A => Aαd | βd

그런 다음 첫 번째 기술을 사용하여 즉시 왼쪽 재귀를 제거하십시오.

A => βdA’
A => αdA’ | ε

이제 프로덕션에는 직접 또는 간접 왼쪽 재귀가 없습니다.

왼쪽 분해

둘 이상의 문법 생산 규칙에 공통 접두사 문자열이있는 경우 하향식 파서가 문자열을 구문 분석하는 데 필요한 생산을 선택할 수 없습니다.

Example

하향식 파서가 다음과 같은 프로덕션을 만나면

A ⟹ αβ | α | …

그러면 두 프로덕션이 동일한 터미널 (또는 비 터미널)에서 시작되므로 문자열을 구문 분석하기 위해 따라야 할 프로덕션을 결정할 수 없습니다. 이러한 혼동을 없애기 위해 왼쪽 인수 분해라는 기술을 사용합니다.

왼쪽 인수 분해는 문법을 하향식 파서에 유용하도록 변환합니다. 이 기술에서 우리는 각 공통 접두사에 대해 하나의 생산을 만들고 나머지 파생은 새로운 생산에 의해 추가됩니다.

Example

위의 제작물은 다음과 같이 쓸 수 있습니다.

A => αA’
A’=> β |  | …

이제 파서는 접두사 당 하나의 프로덕션 만 있으므로 결정을 더 쉽게 수행 할 수 있습니다.

첫 번째 및 후속 세트

파서 테이블 구성의 중요한 부분은 먼저 생성하고 집합을 따르는 것입니다. 이러한 집합은 파생에서 터미널의 실제 위치를 제공 할 수 있습니다. 이것은 T [A, t] = α를 일부 생산 규칙으로 대체하기로 결정한 파싱 테이블을 생성하기 위해 수행됩니다.

첫 번째 세트

이 세트는 비 터미널에 의해 첫 번째 위치에서 파생 된 터미널 기호를 알기 위해 작성됩니다. 예를 들면

α → t β

즉, α는 첫 번째 위치에서 t (터미널)를 유도합니다. 그래서 t ∈ FIRST (α).

첫 번째 집합 계산 알고리즘

FIRST (α) 집합의 정의를보십시오.

α가 터미널이면 FIRST (α) = {α}입니다.
α가 비 말단이고 α → ℇ이 생산이면 FIRST (α) = {ℇ}입니다.
α가 비 말단이고 α → 1 2 3… n이고 FIRST ()에 t가 포함되어 있으면 t는 FIRST (α)에 있습니다.

첫 번째 세트는 다음과 같이 볼 수 있습니다. FIRST (α) = {t | α → ^* t β} ∪ {ℇ | α → ^* ε}

세트 따르기

마찬가지로 생산 규칙에서 비단 말 α 바로 뒤에 오는 종결 기호를 계산합니다. 우리는 비 터미널이 생성 할 수있는 것을 고려하지 않고 대신 비 터미널의 생성을 따르는 다음 터미널 심볼이 무엇인지 봅니다.

Follow set 계산 알고리즘 :

α가 시작 기호이면 FOLLOW () = $
α가 비 말단이고 생산 α → AB를 갖는 경우 FIRST (B)는 ℇ를 제외하고 FOLLOW (A)에 있습니다.
α가 비 말단이고 생산 α → AB (여기서 B ℇ)가있는 경우 FOLLOW (A)는 FOLLOW (α)에 있습니다.

팔로우 세트는 다음과 같이 볼 수 있습니다. FOLLOW (α) = {t | S * αt *}

오류 복구 전략

파서는 프로그램의 오류를 감지하고보고 할 수 있어야합니다. 오류가 발생하면 파서가 오류를 처리하고 나머지 입력을 구문 분석 할 수 있어야합니다. 대부분 파서에서 오류를 확인해야하지만 컴파일 프로세스의 다양한 단계에서 오류가 발생할 수 있습니다. 프로그램에는 다양한 단계에서 다음과 같은 종류의 오류가있을 수 있습니다.

Lexical : 잘못 입력 된 일부 식별자의 이름
Syntactical : 세미콜론 누락 또는 균형이 맞지 않는 괄호
Semantical : 호환되지 않는 값 할당
Logical : 코드에 연결할 수 없음, 무한 루프

코드의 오류를 처리하기 위해 파서에서 구현할 수있는 네 가지 일반적인 오류 복구 전략이 있습니다.

패닉 모드

구문 분석기가 명령문의 어느 곳에서나 오류를 발견하면 세미콜론과 같은 잘못된 입력에서 구분 기호로의 입력을 처리하지 않음으로써 나머지 명령문을 무시합니다. 이것은 오류 복구의 가장 쉬운 방법이며 파서가 무한 루프를 개발하는 것을 방지합니다.

문 모드

구문 분석기에 오류가 발생하면 구문의 나머지 입력이 구문 분석기가 미리 구문 분석 할 수 있도록 수정 조치를 취합니다. 예를 들어, 누락 된 세미콜론 삽입, 쉼표를 세미콜론으로 대체 등. 파서 설계자는 잘못된 수정이 무한 루프로 이어질 수 있으므로 여기서주의해야합니다.

오류 제작

코드에서 발생할 수있는 몇 가지 일반적인 오류는 컴파일러 설계자에게 알려져 있습니다. 또한 디자이너는 이러한 오류가 발생할 때 잘못된 구성을 생성하는 프로덕션으로 사용할 증강 문법을 만들 수 있습니다.

전역 보정

파서는 프로그램을 전체로 간주하고 프로그램이 무엇을 하려는지 알아 내고 가장 근접한 일치 항목을 찾으려고 시도합니다. 이는 오류가 없습니다. 잘못된 입력 (문) X가 제공되면 가장 가까운 오류없는 명령문 Y에 대한 구문 분석 트리를 생성합니다. 이렇게하면 구문 분석기가 소스 코드에서 최소한의 변경을 수행 할 수 있지만 복잡성 (시간 및 공간)으로 인해 이 전략은 아직 실제로 구현되지 않았습니다.

추상 구문 트리

구문 분석 트리 표현은 실제로 필요한 것보다 더 많은 세부 정보를 포함하므로 컴파일러에서 구문 분석하기가 쉽지 않습니다. 다음 구문 분석 트리를 예로 들어 보겠습니다.

자세히 살펴보면 대부분의 리프 노드가 부모 노드의 단일 자식임을 알 수 있습니다. 이 정보는 다음 단계로 전달하기 전에 제거 할 수 있습니다. 추가 정보를 숨기면 아래와 같이 트리를 얻을 수 있습니다.

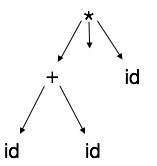
추상 트리는 다음과 같이 나타낼 수 있습니다.

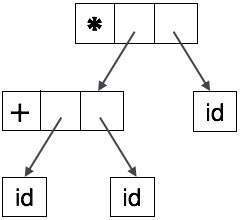
AST는 불필요한 정보가 가장 적은 컴파일러에서 중요한 데이터 구조입니다. AST는 구문 분석 트리보다 더 간결하며 컴파일러에서 쉽게 사용할 수 있습니다.

구문 분석기의 한계

구문 분석기는 어휘 분석기로부터 토큰 형태로 입력을받습니다. 어휘 분석기는 구문 분석기가 제공하는 토큰의 유효성을 담당합니다. 구문 분석기에는 다음과 같은 단점이 있습니다.

토큰이 유효한지 확인할 수 없습니다.
토큰이 사용되기 전에 선언되었는지 확인할 수 없습니다.
토큰이 사용되기 전에 초기화되었는지 확인할 수 없습니다.
토큰 유형에 대해 수행 된 작업이 유효한지 여부를 확인할 수 없습니다.

이러한 작업은 의미 분석에서 연구 할 의미 분석기에 의해 수행됩니다.

구문 분석 단계에서 구문 분석기가 구문 분석 트리를 구성하는 방법을 배웠습니다. 해당 단계에서 생성 된 일반 구문 분석 트리는 트리를 평가하는 방법에 대한 정보를 전달하지 않기 때문에 일반적으로 컴파일러에 사용되지 않습니다. 언어의 규칙을 만드는 문맥없는 문법의 생산은 그것을 해석하는 방법을 수용하지 않습니다.

예를 들면

E → E + T

위의 CFG 제작에는 관련된 의미 규칙이 없으며 제작을 이해하는 데 도움이되지 않습니다.

의미론

언어의 의미는 토큰 및 구문 구조와 같은 구문에 의미를 제공합니다. 의미론은 기호, 유형 및 서로 간의 관계를 해석하는 데 도움이됩니다. 시맨틱 분석은 소스 프로그램에서 구성한 구문 구조가 의미를 도출하는지 여부를 판단합니다.

CFG + semantic rules = Syntax Directed Definitions

예를 들면 :

int a = “value”;

어휘 및 구문 분석 단계에서 어휘 및 구조적으로 정확하므로 오류를 발행해서는 안되지만 할당 유형이 다르기 때문에 의미 오류를 생성해야합니다. 이러한 규칙은 언어의 문법에 의해 설정되고 의미 분석에서 평가됩니다. 의미 분석에서 다음 작업을 수행해야합니다.

범위 해결
유형 검사
배열 바인딩 검사

의미 오류

시맨틱 분석기가 인식 할 것으로 예상되는 몇 가지 시맨틱 오류에 대해 언급했습니다.

유형 불일치
선언되지 않은 변수
예약 된 식별자 오용.
범위에서 변수의 다중 선언.
범위를 벗어난 변수에 액세스합니다.
실제 및 형식 매개 변수가 일치하지 않습니다.

속성 문법

속성 문법은 문맥에 민감한 정보를 제공하기 위해 하나 이상의 비 터미널에 몇 가지 추가 정보 (속성)가 추가되는 특수한 형태의 문맥없는 문법입니다. 각 속성에는 정수, 부동 소수점, 문자, 문자열 및 표현식과 같이 잘 정의 된 값 도메인이 있습니다.

속성 문법은 문맥없는 문법에 의미를 제공하는 매체이며 프로그래밍 언어의 구문과 의미를 지정하는 데 도움이 될 수 있습니다. 속성 문법 (파스 트리로 볼 때)은 트리의 노드간에 값이나 정보를 전달할 수 있습니다.

Example:

E → E + T { E.value = E.value + T.value }

CFG의 오른쪽 부분에는 문법을 해석하는 방법을 지정하는 의미 규칙이 포함되어 있습니다. 여기서는 비단 자 E와 T의 값을 더하고 결과가 비단 자 E에 복사됩니다.

시맨틱 속성은 구문 분석시 도메인의 값에 할당되고 할당 또는 조건시 평가 될 수 있습니다. 속성이 값을 얻는 방식에 따라 크게 합성 속성과 상속 속성의 두 가지 범주로 나눌 수 있습니다.

합성 된 속성

이러한 속성은 하위 노드의 속성 값에서 값을 가져옵니다. 설명을 위해 다음 프로덕션을 가정하십시오.

S → ABC

S가 자식 노드 (A, B, C)에서 값을 가져 오는 경우 ABC의 값이 S로 합성되므로 합성 된 속성이라고합니다.

이전 예제 (E → E + T)에서와 같이 부모 노드 E는 자식 노드에서 값을 가져옵니다. 합성 된 속성은 상위 노드 또는 형제 노드에서 값을 가져 오지 않습니다.

상속 된 속성

합성 된 속성과 달리 상속 된 속성은 부모 및 / 또는 형제로부터 값을받을 수 있습니다. 다음 제작에서와 같이

S → ABC

A는 S, B 및 C에서 값을 가져올 수 있습니다. B는 S, A 및 C에서 값을 가져올 수 있습니다. 마찬가지로 C는 S, A 및 B에서 값을 가져올 수 있습니다.

Expansion : 문법 규칙에 따라 터미널이 아닌 터미널을 터미널로 확장 한 경우

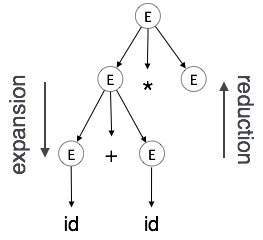
Reduction: 터미널이 문법 규칙에 따라 해당 비 터미널로 축소 된 경우. 구문 트리는 하향식 및 왼쪽에서 오른쪽으로 구문 분석됩니다. 감소가 발생할 때마다 해당 의미 규칙 (액션)을 적용합니다.

시맨틱 분석은 구문 지시 번역을 사용하여 위의 작업을 수행합니다.

시맨틱 분석기는 이전 단계 (구문 분석)에서 AST (Abstract Syntax Tree)를 수신합니다.

시맨틱 분석기는 Attributed AST라고하는 AST와 함께 속성 정보를 첨부합니다.

속성은 두 개의 튜플 값, <속성 이름, 속성 값>입니다.

예를 들면 :

int value  = 5;
<type, “integer”>
<presentvalue, “5”>

모든 프로덕션에 의미 규칙을 첨부합니다.

S- 기여 SDT

SDT가 합성 된 속성 만 사용하는 경우 S- 속성 SDT라고합니다. 이러한 속성은 생산 후 (오른쪽) 시맨틱 동작이 기록 된 S 속성 SDT를 사용하여 평가됩니다.

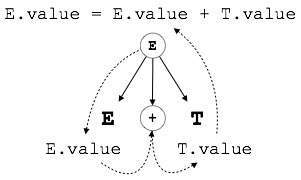
위에서 설명한 것처럼 S- 속성 SDT의 속성은 상위 노드의 값이 하위 노드의 값에 따라 달라 지므로 상향식 구문 분석에서 평가됩니다.

L- 기여 SDT

이 형식의 SDT는 오른쪽 형제에서 값을 가져 오지 않는 제한과 함께 합성 및 상속 된 속성을 모두 사용합니다.

L 속성 SDT에서 비 터미널은 부모, 자식 및 형제 노드에서 값을 가져올 수 있습니다. 다음 생산에서와 같이

S → ABC

S는 A, B, C (합성)에서 값을 취할 수 있습니다. A는 S에서만 값을 가져올 수 있습니다. B는 S와 A에서 값을 가져올 수 있습니다. C는 S, A, B에서 값을 가져올 수 있습니다. 비 터미널은 오른쪽 형제에서 값을 가져올 수 없습니다.

L 속성 SDT의 속성은 깊이 우선 및 왼쪽에서 오른쪽 구문 분석 방식으로 평가됩니다.

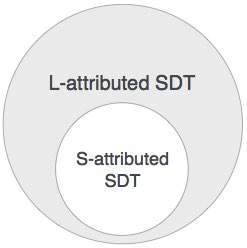
정의가 S- 속성이면 L- 속성 정의가 S- 속성 정의를 포함하므로 L- 속성이라고 결론을 내릴 수 있습니다.

이전 장에서 우리는 구문 분석과 관련된 기본 개념을 이해했습니다. 이 장에서는 사용 가능한 다양한 유형의 파서 생성 방법을 배웁니다.

구문 분석은 구문 분석 트리가 구성되는 방식에 따라 하향식 또는 상향식으로 정의 할 수 있습니다.

하향식 구문 분석

우리는 지난 장에서 하향식 파싱 기술이 입력을 파싱하고 루트 노드에서 점차적으로 리프 노드로 이동하는 파스 트리를 구성하기 시작한다는 것을 배웠습니다. 하향식 구문 분석 유형은 다음과 같습니다.

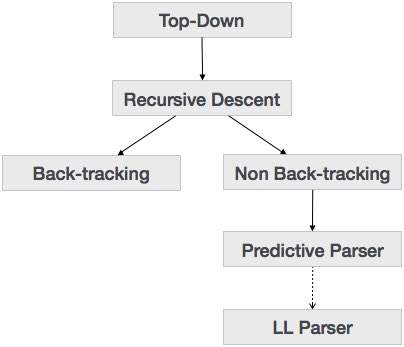
재귀 하강 파싱

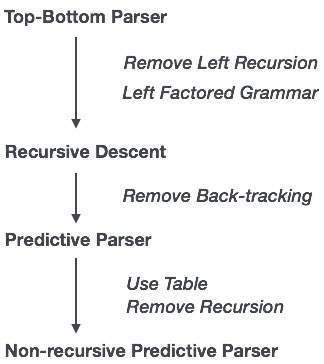
재귀 하강은 위에서부터 구문 분석 트리를 구성하고 입력을 왼쪽에서 오른쪽으로 읽는 하향식 구문 분석 기술입니다. 모든 터미널 및 비 터미널 엔티티에 대한 절차를 사용합니다. 이 구문 분석 기술은 역 추적이 필요할 수도 있고 필요하지 않을 수도있는 구문 분석 트리를 만들기 위해 입력을 재귀 적으로 구문 분석합니다. 그러나 그것과 관련된 문법은 (만약 그대로 두지 않는다면) 역 추적을 피할 수 없습니다. 역 추적을 필요로하지 않는 재귀 하강 파싱의 한 형태는predictive parsing.

이 구문 분석 기술은 본질적으로 재귀적인 문맥없는 문법을 사용하기 때문에 재귀적인 것으로 간주됩니다.

역 추적

하향식 파서는 루트 노드 (시작 기호)에서 시작하고 입력 문자열을 프로덕션 규칙과 일치시켜 대체합니다 (일치하는 경우). 이를 이해하려면 CFG의 다음 예를 살펴보십시오.

S → rXd | rZd
X → oa | ea
Z → ai

입력 문자열의 경우 : 하향식 파서 인 read는 다음과 같이 작동합니다.

생산 규칙의 S로 시작하여 입력의 가장 왼쪽 문자 인 'r'에 수율을 일치시킵니다. S (S → rXd)의 생산이 그것과 일치합니다. 따라서 하향식 파서는 다음 입력 문자 (예 : 'e')로 진행합니다. 파서는 터미널이 아닌 'X'를 확장하고 왼쪽에서 생산을 확인합니다 (X → oa). 다음 입력 기호와 일치하지 않습니다. 따라서 하향식 구문 분석기는 X의 다음 생산 규칙 (X → ea)을 얻기 위해 역 추적합니다.

이제 파서는 모든 입력 문자를 순서대로 일치시킵니다. 문자열이 허용됩니다.

예측 파서

예측 파서는 재귀 하강 파서로 입력 문자열을 대체하는 데 사용할 프로덕션을 예측할 수있는 기능이 있습니다. 예측 파서는 역 추적을 겪지 않습니다.

작업을 수행하기 위해 예측 파서는 다음 입력 기호를 가리키는 미리보기 포인터를 사용합니다. 파서 역 추적을 무료로 만들기 위해 예측 파서는 문법에 몇 가지 제약을두고 LL (k) 문법으로 알려진 문법 클래스 만 허용합니다.

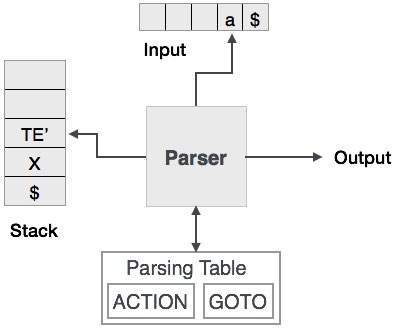
예측 구문 분석은 스택과 구문 분석 테이블을 사용하여 입력을 구문 분석하고 구문 분석 트리를 생성합니다. 스택과 입력 모두에 종료 기호가 있습니다.$스택이 비어 있고 입력이 소비됨을 나타냅니다. 구문 분석기는 입력 및 스택 요소 조합에 대한 결정을 내리기 위해 구문 분석 테이블을 참조합니다.

재귀 하강 파싱에서 파서는 단일 입력 인스턴스에 대해 선택할 수있는 프로덕션이 둘 이상있을 수 있지만 예측 파서에서는 각 단계에 선택할 프로덕션이 하나만 있습니다. 입력 문자열과 일치하는 프로덕션이 없어 구문 분석 절차가 실패하는 경우가있을 수 있습니다.

LL 파서

LL 파서는 LL 문법을 받아들입니다. LL 문법은 문맥없는 문법의 하위 집합이지만 쉽게 구현할 수 있도록 단순화 된 버전을 얻기위한 몇 가지 제한 사항이 있습니다. LL 문법은 두 알고리즘 즉, 재귀 하강 또는 테이블 기반 알고리즘을 통해 구현할 수 있습니다.

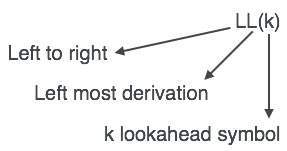
LL 구문 분석기는 LL (k)로 표시됩니다. LL (k)의 첫 번째 L은 왼쪽에서 오른쪽으로 입력을 구문 분석하고, LL (k)의 두 번째 L은 가장 왼쪽에서 파생 된 값을 나타내며 k 자체는 예측 횟수를 나타냅니다. 일반적으로 k = 1이므로 LL (k)도 LL (1)로 쓸 수 있습니다.

LL 구문 분석 알고리즘

파서 설명을 위해 결정 론적 LL (1)을 고수 할 수 있습니다. 테이블의 크기가 k 값에 따라 기하 급수적으로 증가하기 때문입니다. 둘째, 주어진 문법이 LL (1)이 아니면 일반적으로 주어진 k에 대해 LL (k)가 아닙니다.

다음은 LL (1) 구문 분석을위한 알고리즘입니다.

Input: 
string ω 
parsing table M for grammar G
Output:
   If ω is in L(G) then left-most derivation of ω,
   error otherwise.

Initial State : $S on stack (with S being start symbol) ω$ in the input buffer

SET ip to point the first symbol of ω$.
repeat
let X be the top stack symbol and a the symbol pointed by ip.
if X∈ V_t or $
if X = a
   POP X and advance ip.
	else
   error()
 	endif
else	/* X is non-terminal */
   if M[X,a] = X → Y1, Y2,... Yk    
POP X
PUSH Yk, Yk-1,... Y1 /* Y1 on top */
   Output the production X → Y1, Y2,... Yk 
   else
   error()
   endif
	endif
until X = $	/* empty stack */

문법 G는 A-> alpha | b는 G의 두 가지 다른 생산물입니다.

터미널이없는 경우 알파와 베타 모두 a로 시작하는 문자열을 파생합니다.
알파와 베타 중 하나만 빈 문자열을 파생 할 수 있습니다.
beta => t이면 alpha는 FOLLOW (A)에서 터미널로 시작하는 문자열을 파생하지 않습니다.

상향식 파싱

상향식 구문 분석은 트리의 리프 노드에서 시작하여 루트 노드에 도달 할 때까지 위쪽 방향으로 작동합니다. 여기서는 문장에서 시작하여 시작 기호에 도달하기 위해 반대 방식으로 생산 규칙을 적용합니다. 아래 주어진 이미지는 사용 가능한 상향식 파서를 보여줍니다.

Shift-Reduce 구문 분석

Shift-reduce 구문 분석은 상향식 구문 분석을 위해 두 가지 고유 한 단계를 사용합니다. 이러한 단계를 시프트 단계 및 감소 단계라고합니다.

Shift step: 이동 단계는 이동 된 기호라고하는 다음 입력 기호로 입력 포인터의 전진을 나타냅니다. 이 기호는 스택에 푸시됩니다. 이동 된 기호는 구문 분석 트리의 단일 노드로 처리됩니다.
Reduce step: 구문 분석기가 완전한 문법 규칙 (RHS)을 찾아서이를 (LHS)로 대체하는 경우이를 감소 단계라고합니다. 이것은 스택의 맨 위에 핸들이있을 때 발생합니다. 이를 줄이기 위해 스택에서 POP 기능이 수행되어 핸들을 튀어 나와 LHS 비 터미널 기호로 대체합니다.

LR 파서

LR 파서는 비재 귀적, 시프트 감소, 상향식 파서입니다. 그것은 가장 효율적인 구문 분석 기술을 만드는 광범위한 문맥 자유 문법을 사용합니다. LR 파서는 LR (k) 파서라고도합니다. 여기서 L은 입력 스트림의 왼쪽에서 오른쪽 스캔을 나타냅니다. R은 역방향으로 가장 오른쪽 파생의 구성을 나타내며 k는 결정을 내리는 미리보기 기호의 수를 나타냅니다.

LR 파서를 구성하는 데 널리 사용되는 세 가지 알고리즘이 있습니다.

SLR (1) – 단순 LR 파서 :
- 최소 클래스의 문법 작업
- 적은 수의 상태, 따라서 매우 작은 테이블
- 간단하고 빠른 시공
LR (1) – LR 파서 :
- LR (1) 문법 전체 세트에서 작동
- 큰 테이블과 많은 상태를 생성합니다.
- 느린 건설
LALR (1) – 미리보기 LR 파서 :
- 중간 크기의 문법 작업
- 상태 수는 SLR (1)과 동일합니다.

LR 구문 분석 알고리즘

다음은 LR 파서의 스켈레톤 알고리즘을 설명합니다.

token = next_token()
repeat forever
   s = top of stack
   if action[s, token] = “shift si” then
   PUSH token
   PUSH si 
   token = next_token()
else if action[s, tpken] = “reduce A::= β“ then 
   POP 2 * |β| symbols
   s = top of stack
   PUSH A
	PUSH goto[s,A]
else if action[s, token] = “accept” then
	return
	else
   error()

LL 대 LR

LL	LR
가장 왼쪽의 파생을 수행합니다.	역으로 가장 오른쪽 파생을 수행합니다.
스택의 루트 비 터미널에서 시작합니다.	스택에서 루트 비 터미널로 끝납니다.
스택이 비어있을 때 종료됩니다.	빈 스택으로 시작합니다.
스택을 사용하여 여전히 예상되는 항목을 지정합니다.	이미 보이는 것을 지정하기 위해 스택을 사용합니다.
구문 분석 트리를 하향식으로 빌드합니다.	구문 분석 트리 상향식을 작성합니다.
스택에서 비 터미널을 계속 꺼내고 해당 오른쪽을 밉니다.	스택에서 오른쪽을 인식하고 팝하고 해당 비 터미널을 푸시합니다.
비 터미널을 확장합니다.	비 터미널을 줄입니다.
스택에서 하나를 꺼내면 터미널을 읽습니다.	스택에 푸시하는 동안 터미널을 읽습니다.
구문 분석 트리의 사전 주문 순회.	구문 분석 트리의 주문 후 순회.

소스 코드로서의 프로그램은 단순히 텍스트 (코드, 명령문 등)의 모음 일 뿐이며이를 활성화하려면 대상 컴퓨터에서 수행 할 작업이 필요합니다. 프로그램은 명령을 실행하기 위해 메모리 리소스가 필요합니다. 프로그램에는 런타임에 실제 메모리 위치와 매핑해야하는 프로 시저, 식별자 등에 대한 이름이 포함되어 있습니다.

런타임이란 실행중인 프로그램을 의미합니다. 런타임 환경은 시스템에서 실행되는 프로세스에 서비스를 제공하기 위해 소프트웨어 라이브러리, 환경 변수 등을 포함 할 수있는 대상 머신의 상태입니다.

런타임 지원 시스템은 주로 실행 가능한 프로그램 자체로 생성되는 패키지이며 프로세스와 런타임 환경 간의 프로세스 통신을 용이하게합니다. 프로그램이 실행되는 동안 메모리 할당 및 할당 해제를 처리합니다.

활성화 트리

프로그램은 여러 절차로 결합 된 일련의 명령입니다. 프로 시저의 명령은 순차적으로 실행됩니다. 프로 시저에는 시작 및 끝 구분 기호가 있으며 그 안에있는 모든 것을 프로 시저 본문이라고합니다. 프로 시저 식별자와 그 안에있는 유한 명령어 시퀀스가 프로 시저의 본문을 구성합니다.

프로 시저의 실행을 활성화라고합니다. 활성화 레코드에는 절차를 호출하는 데 필요한 모든 정보가 포함되어 있습니다. 활성화 레코드에는 다음 단위가 포함될 수 있습니다 (사용 된 소스 언어에 따라 다름).

임시	식의 임시 및 중간 값을 저장합니다.
로컬 데이터	호출 된 프로 시저의 로컬 데이터를 저장합니다.
기계 상태	프로 시저가 호출되기 전에 레지스터, 프로그램 카운터 등과 같은 기계 상태를 저장합니다.
제어 링크	호출자 프로 시저의 활성화 레코드 주소를 저장합니다.
액세스 링크	로컬 범위를 벗어난 데이터 정보를 저장합니다.
실제 매개 변수	실제 매개 변수, 즉 호출 된 프로 시저에 입력을 보내는 데 사용되는 매개 변수를 저장합니다.
반환 값	반환 값을 저장합니다.

프로 시저가 실행될 때마다 활성화 레코드가 제어 스택이라고도하는 스택에 저장됩니다. 프로 시저가 다른 프로 시저를 호출하면 호출 된 프로 시저가 실행을 완료 할 때까지 호출자의 실행이 일시 중단됩니다. 이때 호출 된 프로 시저의 활성화 레코드가 스택에 저장됩니다.

프로그램 제어가 순차적으로 흐르고 프로 시저가 호출되면 해당 제어가 호출 된 프로 시저로 전달된다고 가정합니다. 호출 된 프로 시저가 실행되면 컨트롤을 호출자에게 반환합니다. 이러한 유형의 제어 흐름을 사용하면 일련의 활성화를 트리 형태로 쉽게 나타낼 수 있습니다.activation tree.

이 개념을 이해하기 위해 코드를 예로 들어 보겠습니다.

. . .
printf(“Enter Your Name: “);
scanf(“%s”, username);
show_data(username);
printf(“Press any key to continue…”);
. . .
int show_data(char *user)
   {
   printf(“Your name is %s”, username);
   return 0;
   }
. . .

아래는 주어진 코드의 활성화 트리입니다.

이제 프로 시저가 깊이 우선 방식으로 실행되므로 스택 할당이 프로 시저 활성화에 가장 적합한 저장 형식이라는 것을 이해합니다.

스토리지 할당

런타임 환경은 다음 엔티티에 대한 런타임 메모리 요구 사항을 관리합니다.

Code: 런타임시 변경되지 않는 프로그램의 텍스트 부분이라고합니다. 메모리 요구 사항은 컴파일 시간에 알려져 있습니다.
Procedures: 텍스트 부분은 정적이지만 무작위로 호출됩니다. 그렇기 때문에 스택 스토리지는 프로 시저 호출 및 활성화를 관리하는 데 사용됩니다.
Variables: 변수는 전역이거나 상수가 아닌 경우 런타임에만 알려져 있습니다. 힙 메모리 할당 체계는 런타임에서 변수에 대한 메모리 할당 및 할당 해제를 관리하는 데 사용됩니다.

정적 할당

이 할당 방식에서 컴파일 데이터는 메모리의 고정 된 위치에 바인딩되며 프로그램이 실행될 때 변경되지 않습니다. 메모리 요구 사항 및 저장 위치가 미리 알려져 있으므로 메모리 할당 및 할당 해제를위한 런타임 지원 패키지가 필요하지 않습니다.

스택 할당

프로 시저 호출 및 해당 활성화는 스택 메모리 할당을 통해 관리됩니다. LIFO (last-in-first-out) 방식으로 작동하며이 할당 전략은 재귀 프로 시저 호출에 매우 유용합니다.

힙 할당

프로 시저에 로컬 인 변수는 런타임시에만 할당 및 할당 해제됩니다. 힙 할당은 변수에 메모리를 동적으로 할당하고 변수가 더 이상 필요하지 않을 때이를 되 돌리는 데 사용됩니다.

정적으로 할당 된 메모리 영역을 제외하고 스택 및 힙 메모리는 모두 동적으로 그리고 예기치 않게 늘어나거나 줄어들 수 있습니다. 따라서 시스템에 고정 된 양의 메모리를 제공 할 수 없습니다.

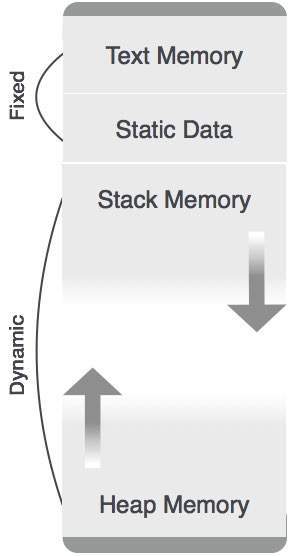
위의 이미지와 같이 코드의 텍스트 부분에는 고정 된 양의 메모리가 할당됩니다. 스택 및 힙 메모리는 프로그램에 할당 된 총 메모리의 극단에 정렬됩니다. 둘 다 수축하고 서로에 대해 성장합니다.

매개 변수 전달

프로 시저 간의 통신 매체를 매개 변수 전달이라고합니다. 호출 프로 시저의 변수 값은 일부 메커니즘에 의해 호출 된 프로 시저로 전송됩니다. 계속 진행하기 전에 먼저 프로그램의 값과 관련된 몇 가지 기본 용어를 살펴보십시오.

r- 값

표현식의 값을 r- 값이라고합니다. 단일 변수에 포함 된 값이 할당 연산자의 오른쪽에 나타나면 r- 값이됩니다. r- 값은 항상 다른 변수에 할당 될 수 있습니다.

l- 값

식이 저장되는 메모리 (주소)의 위치를 해당 식의 l- 값이라고합니다. 항상 할당 연산자의 왼쪽에 나타납니다.

예를 들면 :

day = 1;
week = day * 7;
month = 1;
year = month * 12;

이 예에서 1, 7, 12와 같은 상수 값과 일, 주, 월 및 연도와 같은 변수는 모두 r- 값을 갖는다는 것을 이해합니다. 변수에만 할당 된 메모리 위치를 나타 내기 때문에 l- 값이 있습니다.

예를 들면 :

7 = x + y;

상수 7은 메모리 위치를 나타내지 않으므로 l 값 오류입니다.

공식 매개 변수

호출자 프로 시저가 전달한 정보를받는 변수를 형식 매개 변수라고합니다. 이러한 변수는 호출 된 함수의 정의에서 선언됩니다.

실제 매개 변수

값 또는 주소가 호출 된 프로 시저에 전달되는 변수를 실제 매개 변수라고합니다. 이러한 변수는 함수 호출에서 인수로 지정됩니다.

Example:

fun_one()
{
   int actual_parameter = 10;
   call fun_two(int actual_parameter);
}
   fun_two(int formal_parameter)
{
   print formal_parameter;
}

형식 매개 변수는 사용 된 매개 변수 전달 기술에 따라 실제 매개 변수의 정보를 보유합니다. 값 또는 주소 일 수 있습니다.

가치로 전달

값에 의한 전달 메커니즘에서 호출 프로시 저는 실제 매개 변수의 r 값을 전달하고 컴파일러는이를 호출 된 프로 시저의 활성화 레코드에 넣습니다. 그런 다음 형식 매개 변수는 호출 프로 시저가 전달한 값을 보유합니다. 형식 매개 변수가 보유한 값이 변경되면 실제 매개 변수에 영향을주지 않아야합니다.

참조로 통과

참조 메커니즘에 의한 전달에서 실제 매개 변수의 l- 값은 호출 된 프로 시저의 활성화 레코드에 복사됩니다. 이런 식으로 호출 된 프로시 저는 이제 실제 매개 변수의 주소 (메모리 위치)를 가지며 형식 매개 변수는 동일한 메모리 위치를 참조합니다. 따라서 형식 매개 변수가 가리키는 값이 변경되면 동일한 값을 가리켜 야하기 때문에 실제 매개 변수에 미치는 영향을 확인해야합니다.

복사-복원 통과

이 매개 변수 전달 메커니즘은 호출 된 프로 시저가 종료 될 때 실제 매개 변수가 변경된다는 점을 제외하면 '참조에 의한 전달'과 유사하게 작동합니다. 함수 호출시 호출 된 프로 시저의 활성화 레코드에 실제 매개 변수의 값이 복사됩니다. 조작 된 경우 형식 매개 변수는 실제 매개 변수에 실시간 영향을 미치지 않지만 (l 값이 전달됨에 따라) 호출 된 프로 시저가 종료되면 형식 매개 변수의 l 값이 실제 매개 변수의 l 값에 복사됩니다.

Example:

int y; 
calling_procedure() 
{
   y = 10;     
   copy_restore(y); //l-value of y is passed
   printf y; //prints 99 
}
copy_restore(int x) 
{     
   x = 99; // y still has value 10 (unaffected)
   y = 0; // y is now 0 
}

이 함수가 종료되면 형식 매개 변수 x의 l- 값이 실제 매개 변수 y에 복사됩니다. 프로 시저가 종료되기 전에 y의 값이 변경 되더라도 x의 l 값이 y의 l 값에 복사되어 참조에 의한 호출처럼 동작합니다.

이름으로 전달

Algol과 같은 언어는 C 언어의 전 처리기처럼 작동하는 새로운 종류의 매개 변수 전달 메커니즘을 제공합니다. 이름 전달 메커니즘에서 호출되는 프로 시저의 이름은 실제 본문으로 대체됩니다. 이름에 의한 전달은 이제 참조에 의한 전달과 같이 실제 매개 변수에서 작동 할 수 있도록 프로 시저 본문의 해당 매개 변수에 대한 프로 시저 호출의 인수 표현식을 텍스트 방식으로 대체합니다.

심볼 테이블은 변수 이름, 함수 이름, 객체, 클래스, 인터페이스 등과 같은 다양한 개체의 발생에 대한 정보를 저장하기 위해 컴파일러에서 생성하고 유지 관리하는 중요한 데이터 구조입니다. 심볼 테이블은 분석과 합성 모두에 사용됩니다. 컴파일러의 일부.

기호 테이블은 사용중인 언어에 따라 다음과 같은 용도로 사용될 수 있습니다.

모든 엔티티의 이름을 구조화 된 양식으로 한 곳에 저장합니다.
변수가 선언되었는지 확인합니다.
유형 검사를 구현하려면 소스 코드의 할당 및 표현식이 의미 상 올바른지 확인합니다.
이름의 범위를 결정합니다 (범위 확인).

기호 테이블은 단순히 선형 또는 해시 테이블 일 수있는 테이블입니다. 다음 형식으로 각 이름에 대한 항목을 유지합니다.

<symbol name,  type,  attribute>

예를 들어, 심볼 테이블이 다음 변수 선언에 대한 정보를 저장해야하는 경우 :

static int interest;

다음과 같은 항목을 저장해야합니다.

<interest, int, static>

속성 절에는 이름과 관련된 항목이 포함됩니다.

이행

컴파일러가 소량의 데이터를 처리하는 경우 기호 테이블은 코드화하기 쉬운 순서없는 목록으로 구현할 수 있지만 작은 테이블에만 적합합니다. 기호 테이블은 다음 방법 중 하나로 구현할 수 있습니다.

선형 (정렬 또는 비 정렬) 목록
이진 검색 트리
해시 테이블

무엇보다도 심볼 테이블은 대부분 해시 테이블로 구현되는데, 소스 코드 심볼 자체는 해시 함수의 키로 취급되고 반환 값은 심볼에 대한 정보입니다.

운영

선형 또는 해시 기호 테이블은 다음 작업을 제공해야합니다.

끼워 넣다()

이 작업은 분석 단계, 즉 토큰이 식별되고 이름이 테이블에 저장되는 컴파일러의 전반부에서 더 자주 사용됩니다. 이 작업은 소스 코드에서 발생하는 고유 이름에 대한 정보를 기호 테이블에 추가하는 데 사용됩니다. 이름이 저장되는 형식 또는 구조는 사용중인 컴파일러에 따라 다릅니다.

소스 코드에서 심볼의 속성은 해당 심볼과 관련된 정보입니다. 이 정보에는 기호에 대한 값, 상태, 범위 및 유형이 포함됩니다. insert () 함수는 기호와 그 속성을 인수로 취하고 정보를 기호 테이블에 저장합니다.

예를 들면 :

int a;

컴파일러는 다음과 같이 처리해야합니다.

insert(a, int);

조회 ()

lookup () 연산은 기호 테이블에서 이름을 검색하여 다음을 결정하는 데 사용됩니다.

기호가 테이블에 존재하는 경우.
사용되기 전에 선언 된 경우.
범위에서 이름이 사용되는 경우.
심볼이 초기화 된 경우.
기호가 여러 번 선언 된 경우.

lookup () 함수의 형식은 프로그래밍 언어에 따라 다릅니다. 기본 형식은 다음과 일치해야합니다.

lookup(symbol)

이 메서드는 기호가 기호 테이블에없는 경우 0 (영)을 반환합니다. 기호가 기호 테이블에 있으면 테이블에 저장된 속성을 반환합니다.

범위 관리

컴파일러는 두 가지 유형의 기호 테이블을 유지합니다. global symbol table 모든 절차를 통해 액세스 할 수 있으며 scope symbol tables 프로그램의 각 범위에 대해 생성됩니다.

이름의 범위를 결정하기 위해 기호 테이블은 아래 예와 같이 계층 구조로 정렬됩니다.

. . . 
int value=10;

void pro_one()
   {
   int one_1;
   int one_2;
   
      {              \
      int one_3;      |_  inner scope 1 
      int one_4;      | 
      }              /
      
   int one_5; 
   
      {              \   
      int one_6;      |_  inner scope 2
      int one_7;      |
      }              /
   }
   
void pro_two()
   {
   int two_1;
   int two_2;
   
      {              \
      int two_3;      |_  inner scope 3
      int two_4;      |
      }              /
      
   int two_5;
   }
. . .

위의 프로그램은 기호 테이블의 계층 구조로 나타낼 수 있습니다.

전역 기호 테이블에는 하나의 전역 변수 (int 값)에 대한 이름과 위에 표시된 모든 자식 노드에서 사용할 수있는 두 개의 프로 시저 이름이 포함됩니다. pro_one 기호 테이블 (및 모든 하위 테이블)에 언급 된 이름은 pro_two 기호 및 해당 하위 테이블에 사용할 수 없습니다.

이 심볼 테이블 데이터 구조 계층은 의미 분석기에 저장되며 심볼 테이블에서 이름을 검색해야 할 때마다 다음 알고리즘을 사용하여 검색됩니다.

먼저 현재 범위, 즉 현재 기호 테이블에서 기호가 검색됩니다.
이름이 발견되면 검색이 완료됩니다. 그렇지 않으면 상위 기호 테이블에서 검색됩니다.
이름이 발견되었거나 글로벌 기호 테이블에서 이름을 검색했습니다.

소스 코드를 대상 기계 코드로 직접 변환 할 수 있습니다. 그러면 소스 코드를 중간 코드로 변환 한 다음 대상 코드로 변환해야하는 이유는 무엇입니까? 중간 코드가 필요한 이유를 살펴 보겠습니다.

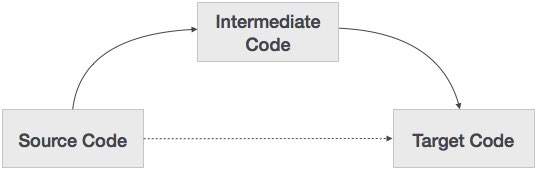
컴파일러가 중간 코드를 생성하는 옵션없이 소스 언어를 대상 기계 언어로 변환하는 경우, 각각의 새 기계에 대해 완전한 원시 컴파일러가 필요합니다.
중간 코드는 모든 컴파일러에 대해 분석 부분을 동일하게 유지함으로써 모든 고유 한 기계에 대해 새로운 완전한 컴파일러의 필요성을 제거합니다.
컴파일러의 두 번째 부분 인 합성은 대상 머신에 따라 변경됩니다.
중간 코드에 코드 최적화 기술을 적용하여 코드 성능을 향상시키기 위해 소스 코드 수정 사항을 적용하는 것이 더 쉬워졌습니다.

중급 표현

중간 코드는 다양한 방식으로 표현 될 수 있으며 고유 한 이점이 있습니다.

High Level IR-고급 중간 코드 표현은 소스 언어 자체에 매우 가깝습니다. 소스 코드에서 쉽게 생성 할 수 있으며 코드 수정을 쉽게 적용하여 성능을 향상시킬 수 있습니다. 그러나 대상 기계 최적화의 경우 덜 선호됩니다.
Low Level IR -이것은 타겟 머신과 가까워서 레지스터 및 메모리 할당, 명령어 세트 선택 등에 적합합니다. 머신 의존적 최적화에 좋습니다.

중간 코드는 특정 언어 (예 : Java 용 바이트 코드) 또는 언어 독립적 (3 주소 코드) 일 수 있습니다.

세 주소 코드

중간 코드 생성기는 주석이 달린 구문 트리의 형태로 이전 단계 인 의미 분석기로부터 입력을받습니다. 그 구문 트리는 예를 들어 접미사 표기법과 같은 선형 표현으로 변환 될 수 있습니다. 중간 코드는 기계 독립 코드 인 경향이 있습니다. 따라서 코드 생성기는 코드를 생성하기 위해 무제한의 메모리 저장소 (레지스터)를 가지고 있다고 가정합니다.

예를 들면 :

a = b + c * d;

중간 코드 생성기는이 표현식을 하위 표현식으로 분할 한 다음 해당 코드를 생성합니다.

r1 = c * d;
r2 = b + r1;
a = r2

r 대상 프로그램에서 레지스터로 사용됩니다.

3 개 주소 코드에는 표현식을 계산할 주소 위치가 최대 3 개 있습니다. 세 주소 코드는 쿼드 러플과 트리플의 두 가지 형태로 표현할 수 있습니다.

쿼드 러플

쿼드 러플 프레젠테이션의 각 명령어는 연산자, arg1, arg2 및 결과의 4 개 필드로 나뉩니다. 위의 예는 아래에 4 중 형식으로 표시됩니다.

Op	인수 ₁	인수 ₂	결과
*	씨	디	r1
+	비	r1	r2
+	r2	r1	r3
=	r3		ㅏ

트리플

트리플 표현의 각 명령어에는 op, arg1 및 arg2의 세 필드가 있으며 각 하위 표현식의 결과는 expression의 위치로 표시됩니다. 트리플은 DAG 및 구문 트리와의 유사성을 나타냅니다. 식을 나타내는 동안 DAG와 동일합니다.

Op	인수 ₁	인수 ₂
*	씨	디
+	비	(0)
+	(1)	(0)
=	(2)

결과는 위치에 따라 다르고 표현식의 순서 나 위치를 변경하면 문제가 발생할 수 있으므로 트리플은 최적화하는 동안 코드 이동성 문제에 직면합니다.

간접 트리플

이 표현은 트리플 표현보다 향상되었습니다. 위치 대신 포인터를 사용하여 결과를 저장합니다. 이를 통해 최적화 프로그램은 하위 표현식을 자유롭게 재배치하여 최적화 된 코드를 생성 할 수 있습니다.

선언

변수 또는 프로 시저를 사용하려면 먼저 선언해야합니다. 선언에는 메모리의 공간 할당과 기호 테이블의 유형 및 이름 입력이 포함됩니다. 대상 기계 구조를 염두에두고 프로그램을 코딩하고 설계 할 수 있지만 소스 코드를 대상 언어로 정확하게 변환하는 것이 항상 가능하지는 않습니다.

전체 프로그램을 프로 시저 및 하위 프로 시저의 모음으로 취하면 모든 이름을 프로 시저에 로컬로 선언 할 수 있습니다. 메모리 할당은 연속적인 방식으로 이루어지며 이름은 프로그램에서 선언 된 순서대로 메모리에 할당됩니다. 오프셋 변수를 사용하고 기본 주소를 나타내는 0 {offset = 0}으로 설정합니다.

소스 프로그래밍 언어와 대상 컴퓨터 아키텍처는 이름이 저장되는 방식이 다를 수 있으므로 상대 주소 지정이 사용됩니다. 첫 번째 이름은 메모리 위치 0 {offset = 0}에서 시작하여 메모리가 할당되지만 나중에 선언 된 다음 이름은 첫 번째 이름 옆에 메모리가 할당되어야합니다.

Example:

정수 변수에 2 바이트의 메모리가 할당되고 부동 변수에 4 바이트의 메모리가 할당되는 C 프로그래밍 언어의 예를 살펴 보겠습니다.

int a;
float b;
Allocation process:
{offset = 0}
int a;
id.type = int
id.width = 2
offset = offset + id.width 
{offset = 2}
float b;
   id.type = float
   id.width = 4
   offset = offset + id.width 
{offset = 6}

이 세부 사항을 기호 테이블에 입력하기 위해 프로 시저 입력을 사용할 수 있습니다. 이 방법은 다음과 같은 구조를 가질 수 있습니다.

enter(name, type, offset)

이 절차는 데이터 영역에서 유형 및 상대 주소 오프셋 으로 설정된 유형을 갖는 변수 name 에 대한 기호 테이블에 항목을 만들어야합니다 .

코드 생성은 컴파일의 마지막 단계로 간주 할 수 있습니다. 포스트 코드 생성을 통해 최적화 프로세스를 코드에 적용 할 수 있지만 이는 코드 생성 단계 자체의 일부로 볼 수 있습니다. 컴파일러에서 생성 된 코드는 어셈블리 언어와 같은 일부 하위 수준 프로그래밍 언어의 개체 코드입니다. 상위 수준 언어로 작성된 소스 코드가 하위 수준 언어로 변환되어 하위 수준의 개체 코드가 생성되는 것을 보았습니다.이 코드는 다음과 같은 최소 속성을 가져야합니다.

소스 코드의 정확한 의미를 전달해야합니다.
CPU 사용 및 메모리 관리 측면에서 효율적이어야합니다.

이제 중간 코드가 대상 객체 코드 (이 경우 어셈블리 코드)로 어떻게 변환되는지 살펴 보겠습니다.

방향성 비순환 그래프

DAG (Directed Acyclic Graph)는 기본 블록의 구조를 묘사하고 기본 블록 사이에 흐르는 값의 흐름을 확인하는 데 도움이되며 최적화도 제공하는 도구입니다. DAG는 기본 블록에 대한 쉬운 변환을 제공합니다. DAG는 여기에서 이해할 수 있습니다.

리프 노드는 식별자, 이름 또는 상수를 나타냅니다.
내부 노드는 연산자를 나타냅니다.
내부 노드는 또한 값이 저장되거나 할당되는 표현식 또는 식별자 / 이름의 결과를 나타냅니다.

Example:

t₀ = a + b
t₁ = t₀ + c
d = t₀ + t₁

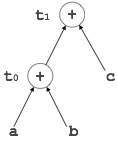
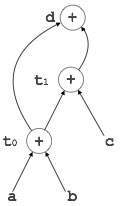
[t ₀ = a + b]	[t ₁ = t ₀ + c]	[d = t ₀ + t ₁ ]

구멍 최적화

이 최적화 기술은 소스 코드에서 로컬로 작동하여 최적화 된 코드로 변환합니다. 로컬이란 코드 블록의 작은 부분을 의미합니다. 이러한 방법은 중간 코드와 대상 코드에 적용 할 수 있습니다. 여러 문이 분석되고 다음과 같은 가능한 최적화가 있는지 확인됩니다.

중복 명령 제거

소스 코드 수준에서 사용자는 다음을 수행 할 수 있습니다.

int add_ten(int x)
   {
   int y, z;
   y = 10;
   z = x + y;
   return z;
   }

int add_ten(int x)
   {
   int y;
   y = 10;
   y = x + y;
   return y;
   }

int add_ten(int x)
   {
   int y = 10;
   return x + y;
   }

int add_ten(int x)
   {
   return x + 10;
   }

컴파일 수준에서 컴파일러는 본질적으로 중복 된 명령어를 검색합니다. 명령어의 다중로드 및 저장은 일부가 제거 되더라도 동일한 의미를 가질 수 있습니다. 예를 들면 :

MOV x, R0
MOV R0, R1

첫 번째 명령어를 삭제하고 문장을 다음과 같이 다시 작성할 수 있습니다.

MOV x, R1

연결할 수없는 코드

연결할 수없는 코드는 프로그래밍 구조로 인해 액세스 할 수없는 프로그램 코드의 일부입니다. 프로그래머는 절대 도달 할 수없는 코드를 실수로 작성했을 수 있습니다.

Example:

void add_ten(int x)
{
   return x + 10;
   printf(“value of x is %d”, x);
}

이 코드 세그먼트에서 printf 프로그램 컨트롤이 실행되기 전에 반환되므로 명령문은 실행되지 않습니다. printf 제거 할 수 있습니다.

제어 최적화의 흐름

프로그램 컨트롤이 중요한 작업을 수행하지 않고 앞뒤로 점프하는 코드의 경우가 있습니다. 이러한 점프는 제거 할 수 있습니다. 다음 코드 덩어리를 고려하십시오.

...		
MOV R1, R2
GOTO L1
...
L1 :   GOTO L2
L2 :   INC R1

이 코드에서 L1 레이블은 컨트롤을 L2로 전달할 때 제거 할 수 있습니다. 따라서 L1으로 점프 한 다음 L2로 점프하는 대신 아래에 표시된 것처럼 컨트롤이 L2에 직접 도달 할 수 있습니다.

...		
MOV R1, R2
GOTO L2
...
L2 :   INC R1

대수 표현 단순화

대수 표현을 간단하게 만들 수있는 경우가 있습니다. 예를 들어, 표현식a = a + 0 대체 가능 a 그 자체와 표현 a = a + 1은 단순히 INC a로 대체 될 수 있습니다.

강도 감소

더 많은 시간과 공간을 소비하는 작업이 있습니다. 이들의 '강도'는 시간과 공간을 덜 소비하지만 동일한 결과를 생성하는 다른 작업으로 대체하여 줄일 수 있습니다.

예를 들면 x * 2 대체 가능 x << 1, 하나의 왼쪽 교대 만 포함됩니다. a * a와 a ² 의 출력 은 동일하지만 a ² 를 구현하는 것이 훨씬 더 효율적입니다.

기계 지침에 액세스

대상 컴퓨터는 특정 작업을 훨씬 효율적으로 수행 할 수있는 더 정교한 명령을 배포 할 수 있습니다. 대상 코드가 이러한 명령을 직접 수용 할 수 있다면 코드의 품질이 향상 될뿐만 아니라보다 효율적인 결과를 얻을 수 있습니다.

코드 생성기

코드 생성기는 대상 머신의 런타임 환경과 해당 명령어 세트를 이해하고 있어야합니다. 코드 생성기는 코드를 생성하기 위해 다음 사항을 고려해야합니다.

Target language: 코드 생성기는 코드를 변환 할 대상 언어의 특성을 알고 있어야합니다. 이 언어는 컴파일러가보다 편리한 방법으로 코드를 생성하는 데 도움이되는 일부 기계 별 명령어를 용이하게 할 수 있습니다. 대상 머신은 CISC 또는 RISC 프로세서 아키텍처를 가질 수 있습니다.
IR Type: 중급 표현에는 다양한 형태가 있습니다. AST (Abstract Syntax Tree) 구조, Reverse Polish Notation 또는 3- 주소 코드 일 수 있습니다.
Selection of instruction: 코드 생성기는 Intermediate Representation을 입력으로 사용하여 대상 컴퓨터의 명령어 세트로 변환 (매핑)합니다. 하나의 표현에는 여러 가지 방법 (명령)이있을 수 있으므로 적절한 명령을 현명하게 선택하는 것은 코드 생성기의 책임이됩니다.
Register allocation: 프로그램에는 실행 중에 유지해야 할 여러 값이 있습니다. 대상 머신의 아키텍처는 모든 값이 CPU 메모리 또는 레지스터에 유지되는 것을 허용하지 않을 수 있습니다. 코드 생성기는 레지스터에 유지할 값을 결정합니다. 또한 이러한 값을 유지하는 데 사용할 레지스터를 결정합니다.
Ordering of instructions: 마지막으로 코드 생성기는 명령이 실행될 순서를 결정합니다. 명령을 실행하기위한 일정을 만듭니다.

설명자

코드 생성기는 코드를 생성하는 동안 레지스터 (가용성)와 주소 (값 위치)를 모두 추적해야합니다. 둘 다에 대해 다음 두 설명이 사용됩니다.

Register descriptor: 레지스터 설명자는 레지스터의 가용성을 코드 생성기에 알리는 데 사용됩니다. 레지스터 설명자는 각 레지스터에 저장된 값을 추적합니다. 코드 생성 중에 새 레지스터가 필요할 때마다이 설명자는 레지스터 가용성을 위해 참조됩니다.
Address descriptor: 프로그램에서 사용되는 이름 (식별자)의 값은 실행 중에 다른 위치에 저장 될 수 있습니다. 주소 설명자는 식별자 값이 저장되는 메모리 위치를 추적하는 데 사용됩니다. 이러한 위치에는 CPU 레지스터, 힙, 스택, 메모리 또는 언급 된 위치의 조합이 포함될 수 있습니다.

코드 생성기는 두 설명자를 실시간으로 업데이트합니다. load 문, LD R1, x, 코드 생성기의 경우 :

값이 x 인 레지스터 설명자 R1을 업데이트하고
주소 설명자 (x)를 업데이트하여 x의 한 인스턴스가 R1에 있음을 나타냅니다.

코드 생성

기본 블록은 일련의 3 개 주소 명령으로 구성됩니다. 코드 생성기는 이러한 명령 시퀀스를 입력으로 사용합니다.

Note: 하나 이상의 위치 (레지스터, 캐시 또는 메모리)에서 이름의 값이 발견되면 레지스터의 값이 캐시 및 메인 메모리보다 우선합니다. 마찬가지로 캐시의 값이 주 메모리보다 선호됩니다. 메인 메모리는 거의 선호하지 않습니다.

getReg: 코드 생성기는 getReg 함수를 사용하여 사용 가능한 레지스터의 상태와 이름 값의 위치를 결정합니다. getReg 는 다음과 같이 작동합니다.

변수 Y가 이미 레지스터 R에 있으면 해당 레지스터를 사용합니다.
그렇지 않으면 레지스터 R을 사용할 수있는 경우 해당 레지스터를 사용합니다.
그렇지 않으면 위의 두 옵션을 모두 사용할 수없는 경우 최소한의로드 및 저장 명령이 필요한 레지스터를 선택합니다.

명령어 x = y OP z의 경우 코드 생성기는 다음 작업을 수행 할 수 있습니다. L이 y OP z의 출력이 저장 될 위치 (가급적 레지스터)라고 가정 해 보겠습니다.

getReg 함수를 호출하여 L의 위치를 결정합니다.
현재 위치 (레지스터 또는 메모리) 확인 y 주소 설명자에게 문의하여 y. 만약y 현재 등록되지 않음 L, 다음 명령을 생성하여 값을 복사하십시오. y ...에 L:

MOV y ', L

어디 y’ 복사 된 값을 나타냅니다. y.
현재 위치 결정 z 2 단계에서 사용한 것과 동일한 방법을 사용하여 y 다음 명령을 생성하십시오.

OP z ', L

어디 z’ 복사 된 값을 나타냅니다. z.
이제 L은 y OP z의 값을 포함합니다. x. 따라서 L이 레지스터 인 경우 설명자를 업데이트하여 값이 포함되어 있음을 나타냅니다.x. 설명자 업데이트x to indicate that it is stored at location L.
If y and z has no further use, they can be given back to the system.

Other code constructs like loops and conditional statements are transformed into assembly language in general assembly way.

Optimization is a program transformation technique, which tries to improve the code by making it consume less resources (i.e. CPU, Memory) and deliver high speed.

In optimization, high-level general programming constructs are replaced by very efficient low-level programming codes. A code optimizing process must follow the three rules given below:

The output code must not, in any way, change the meaning of the program.
Optimization should increase the speed of the program and if possible, the program should demand less number of resources.
Optimization should itself be fast and should not delay the overall compiling process.

Efforts for an optimized code can be made at various levels of compiling the process.

At the beginning, users can change/rearrange the code or use better algorithms to write the code.
After generating intermediate code, the compiler can modify the intermediate code by address calculations and improving loops.
While producing the target machine code, the compiler can make use of memory hierarchy and CPU registers.

Optimization can be categorized broadly into two types : machine independent and machine dependent.

Machine-independent Optimization

In this optimization, the compiler takes in the intermediate code and transforms a part of the code that does not involve any CPU registers and/or absolute memory locations. For example:

do
{
   item = 10;
   value = value + item; 
}while(value<100);

This code involves repeated assignment of the identifier item, which if we put this way:

Item = 10;
do
{
   value = value + item; 
} while(value<100);

should not only save the CPU cycles, but can be used on any processor.

Machine-dependent Optimization

Machine-dependent optimization is done after the target code has been generated and when the code is transformed according to the target machine architecture. It involves CPU registers and may have absolute memory references rather than relative references. Machine-dependent optimizers put efforts to take maximum advantage of memory hierarchy.

Basic Blocks

Source codes generally have a number of instructions, which are always executed in sequence and are considered as the basic blocks of the code. These basic blocks do not have any jump statements among them, i.e., when the first instruction is executed, all the instructions in the same basic block will be executed in their sequence of appearance without losing the flow control of the program.

A program can have various constructs as basic blocks, like IF-THEN-ELSE, SWITCH-CASE conditional statements and loops such as DO-WHILE, FOR, and REPEAT-UNTIL, etc.

Basic block identification

We may use the following algorithm to find the basic blocks in a program:

Search header statements of all the basic blocks from where a basic block starts:
- First statement of a program.
- Statements that are target of any branch (conditional/unconditional).
- Statements that follow any branch statement.
Header statements and the statements following them form a basic block.
A basic block does not include any header statement of any other basic block.

Basic blocks are important concepts from both code generation and optimization point of view.

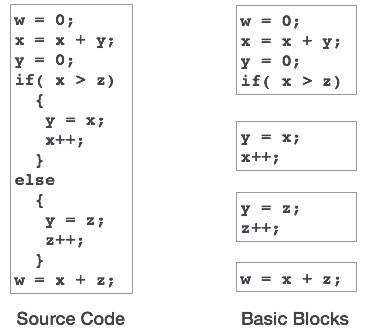
Basic blocks play an important role in identifying variables, which are being used more than once in a single basic block. If any variable is being used more than once, the register memory allocated to that variable need not be emptied unless the block finishes execution.

Control Flow Graph

Basic blocks in a program can be represented by means of control flow graphs. A control flow graph depicts how the program control is being passed among the blocks. It is a useful tool that helps in optimization by help locating any unwanted loops in the program.

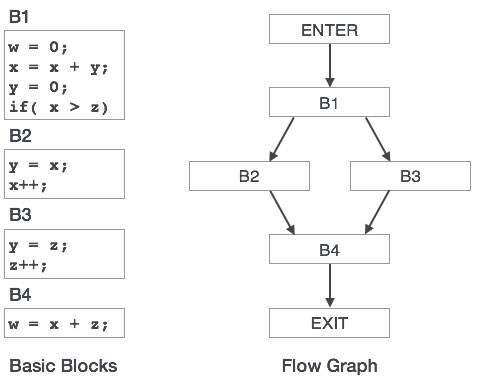
Loop Optimization

Most programs run as a loop in the system. It becomes necessary to optimize the loops in order to save CPU cycles and memory. Loops can be optimized by the following techniques:

Invariant code : A fragment of code that resides in the loop and computes the same value at each iteration is called a loop-invariant code. This code can be moved out of the loop by saving it to be computed only once, rather than with each iteration.
Induction analysis : A variable is called an induction variable if its value is altered within the loop by a loop-invariant value.
Strength reduction : There are expressions that consume more CPU cycles, time, and memory. These expressions should be replaced with cheaper expressions without compromising the output of expression. For example, multiplication (x * 2) is expensive in terms of CPU cycles than (x << 1) and yields the same result.

Dead-code Elimination

Dead code is one or more than one code statements, which are:

Either never executed or unreachable,
Or if executed, their output is never used.

Thus, dead code plays no role in any program operation and therefore it can simply be eliminated.

Partially dead code

There are some code statements whose computed values are used only under certain circumstances, i.e., sometimes the values are used and sometimes they are not. Such codes are known as partially dead-code.

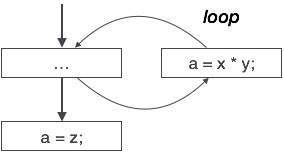
The above control flow graph depicts a chunk of program where variable ‘a’ is used to assign the output of expression ‘x * y’. Let us assume that the value assigned to ‘a’ is never used inside the loop.Immediately after the control leaves the loop, ‘a’ is assigned the value of variable ‘z’, which would be used later in the program. We conclude here that the assignment code of ‘a’ is never used anywhere, therefore it is eligible to be eliminated.

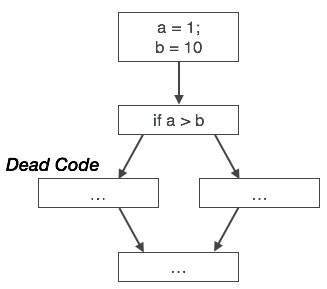
Likewise, the picture above depicts that the conditional statement is always false, implying that the code, written in true case, will never be executed, hence it can be removed.

Partial Redundancy

Redundant expressions are computed more than once in parallel path, without any change in operands.whereas partial-redundant expressions are computed more than once in a path, without any change in operands. For example,

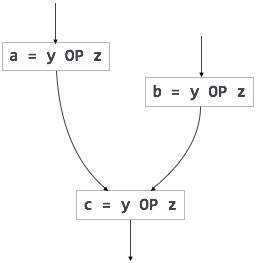
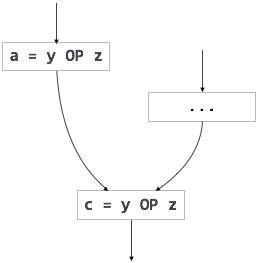
[redundant expression]	[partially redundant expression]

Loop-invariant code is partially redundant and can be eliminated by using a code-motion technique.

Another example of a partially redundant code can be:

If (condition)
{
   a = y OP z;
}
else
{
   ...
}
c = y OP z;

We assume that the values of operands (y and z) are not changed from assignment of variable a to variable c. Here, if the condition statement is true, then y OP z is computed twice, otherwise once. Code motion can be used to eliminate this redundancy, as shown below:

If (condition)
{
   ...
   tmp = y OP z;
   a = tmp;
   ...
}
else
{
   ...
   tmp = y OP z;
}
c = tmp;

Here, whether the condition is true or false; y OP z should be computed only once.