컴파일러 설계-하향식 파서
우리는 마지막 장에서 하향식 파싱 기술이 입력을 파싱하고 루트 노드에서 점차적으로 리프 노드로 이동하는 파스 트리 구성을 시작한다는 것을 배웠습니다. 하향식 구문 분석 유형은 다음과 같습니다.
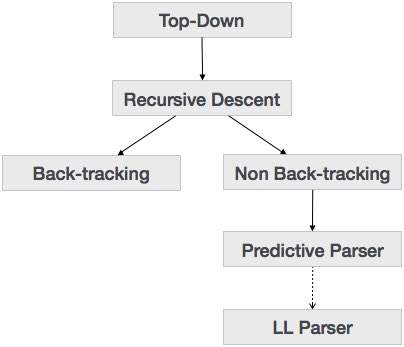
재귀 하강 파싱
재귀 하강은 위에서부터 구문 분석 트리를 구성하고 입력을 왼쪽에서 오른쪽으로 읽는 하향식 구문 분석 기술입니다. 모든 터미널 및 비 터미널 엔티티에 대한 절차를 사용합니다. 이 구문 분석 기술은 역 추적이 필요할 수도 있고 필요하지 않을 수도있는 구문 분석 트리를 만들기 위해 입력을 재귀 적으로 구문 분석합니다. 그러나 그것과 관련된 문법은 (만약 고려하지 않는다면) 역 추적을 피할 수 없습니다. 역 추적을 필요로하지 않는 재귀 하강 구문 분석의 한 형태는predictive parsing.
이 구문 분석 기술은 본질적으로 재귀적인 문맥없는 문법을 사용하기 때문에 재귀적인 것으로 간주됩니다.
역 추적
하향식 파서는 루트 노드 (시작 기호)에서 시작하고 입력 문자열을 프로덕션 규칙과 일치시켜 대체합니다 (일치하는 경우). 이를 이해하려면 CFG의 다음 예를 살펴보십시오.
S → rXd | rZd
X → oa | ea
Z → ai입력 문자열의 경우 : 하향식 파서 인 read는 다음과 같이 작동합니다.
생산 규칙의 S로 시작하여 입력의 가장 왼쪽 문자 인 'r'에 수율을 일치시킵니다. S (S → rXd)의 생산 자체가 그것과 일치합니다. 따라서 하향식 파서는 다음 입력 문자 (예 : 'e')로 이동합니다. 파서는 터미널이 아닌 'X'를 확장하고 왼쪽에서 생산을 확인합니다 (X → oa). 다음 입력 기호와 일치하지 않습니다. 따라서 하향식 구문 분석기는 X의 다음 생산 규칙 (X → ea)을 얻기 위해 역 추적합니다.
이제 파서는 모든 입력 문자를 순서대로 일치시킵니다. 문자열이 허용됩니다.
|
|
|
|
|
예측 파서
예측 파서는 재귀 하강 파서로, 입력 문자열을 대체하는 데 사용할 프로덕션을 예측하는 기능이 있습니다. 예측 파서는 역 추적을 겪지 않습니다.
작업을 수행하기 위해 예측 파서는 다음 입력 기호를 가리키는 미리보기 포인터를 사용합니다. 파서 역 추적을 무료로 만들기 위해 예측 파서는 문법에 몇 가지 제약을두고 LL (k) 문법으로 알려진 문법 클래스 만 허용합니다.
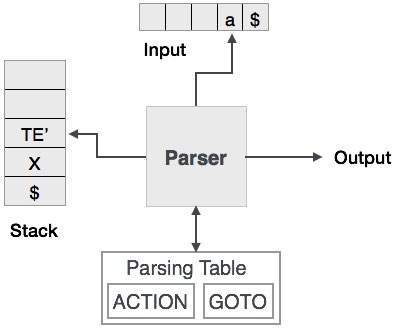
예측 구문 분석은 스택과 구문 분석 테이블을 사용하여 입력을 구문 분석하고 구문 분석 트리를 생성합니다. 스택과 입력 모두에 종료 기호가 있습니다.$스택이 비어 있고 입력이 소비되었음을 나타냅니다. 구문 분석기는 입력 및 스택 요소 조합에 대한 결정을 내리기 위해 구문 분석 테이블을 참조합니다.
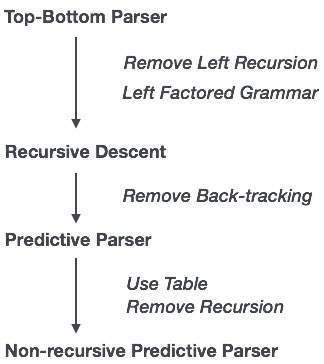
재귀 적 하강 파싱에서 파서는 단일 입력 인스턴스에 대해 하나 이상의 프로덕션을 선택할 수있는 반면, 예측 파서에서는 각 단계에 선택할 프로덕션이 하나만 있습니다. 입력 문자열과 일치하는 프로덕션이 없어 구문 분석 절차가 실패하는 경우가있을 수 있습니다.
LL 파서
LL 파서는 LL 문법을 받아들입니다. LL 문법은 문맥없는 문법의 하위 집합이지만 쉽게 구현할 수 있도록 단순화 된 버전을 얻기위한 몇 가지 제한 사항이 있습니다. LL 문법은 두 알고리즘 즉, 재귀 하강 또는 테이블 기반 알고리즘을 통해 구현할 수 있습니다.
LL 구문 분석기는 LL (k)로 표시됩니다. LL (k)의 첫 번째 L은 왼쪽에서 오른쪽으로 입력을 구문 분석하고, LL (k)의 두 번째 L은 가장 왼쪽에서 파생 된 값을 나타내며 k 자체는 예측 횟수를 나타냅니다. 일반적으로 k = 1이므로 LL (k)도 LL (1)로 쓸 수 있습니다.
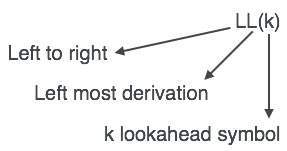
LL 구문 분석 알고리즘
파서 설명을 위해 결정 론적 LL (1)을 고수 할 수 있습니다. 테이블의 크기가 k 값에 따라 기하 급수적으로 증가하기 때문입니다. 둘째, 주어진 문법이 LL (1)이 아니면 일반적으로 주어진 k에 대해 LL (k)가 아닙니다.
다음은 LL (1) 구문 분석에 대한 알고리즘입니다.
Input:
string ω
parsing table M for grammar G
Output:
If ω is in L(G) then left-most derivation of ω,
error otherwise.
Initial State : $S on stack (with S being start symbol)
ω$ in the input buffer
SET ip to point the first symbol of ω$.
repeat
let X be the top stack symbol and a the symbol pointed by ip.
if X∈ Vt or $
if X = a
POP X and advance ip.
else
error()
endif
else /* X is non-terminal */
if M[X,a] = X → Y1, Y2,... Yk
POP X
PUSH Yk, Yk-1,... Y1 /* Y1 on top */
Output the production X → Y1, Y2,... Yk
else
error()
endif
endif
until X = $ /* empty stack */A → α | 경우 문법 G는 LL (1)입니다. β는 G의 두 가지 별개의 생산물입니다.
터미널이없는 경우 α와 β는 모두 a로 시작하는 문자열을 파생합니다.
α와 β 중 하나만 빈 문자열을 파생 할 수 있습니다.
β → t이면 α는 FOLLOW (A)에서 터미널로 시작하는 문자열을 파생하지 않습니다.