분류 알고리즘-로지스틱 회귀

로지스틱 회귀 소개

로지스틱 회귀는 대상 변수의 확률을 예측하는 데 사용되는지도 학습 분류 알고리즘입니다. 대상 또는 종속 변수의 특성은 이분법 적이므로 가능한 클래스는 두 개뿐입니다.

간단히 말해서 종속 변수는 본질적으로 데이터가 1 ​​(성공 / 예) 또는 0 (실패 / 아니오)으로 코딩 된 이진입니다.

수학적으로 로지스틱 회귀 모델은 P (Y = 1)를 X의 함수로 예측합니다. 스팸 탐지, 당뇨병 예측, 암 탐지 등과 같은 다양한 분류 문제에 사용할 수있는 가장 간단한 ML 알고리즘 중 하나입니다.

로지스틱 회귀 유형

일반적으로 로지스틱 회귀는 이진 목표 변수를 갖는 이진 로지스틱 회귀를 의미하지만 이에 의해 예측할 수있는 목표 변수의 범주가 두 개 더있을 수 있습니다. 이러한 범주의 수를 기반으로 로지스틱 회귀는 다음 유형으로 나눌 수 있습니다.

이진 또는 이항

이러한 종류의 분류에서 종속 변수는 1과 0의 두 가지 가능한 유형 만 가질 수 있습니다. 예를 들어, 이러한 변수는 성공 또는 실패, 예 또는 아니오, 승패 등을 나타낼 수 있습니다.

다항식

이러한 종류의 분류에서 종속 변수는 순서가 지정되지 않은 3 개 이상의 유형 또는 양적 유의성이없는 유형을 가질 수 있습니다. 예를 들어, 이러한 변수는 "유형 A"또는 "유형 B"또는 "유형 C"를 나타낼 수 있습니다.

서수

이러한 종류의 분류에서 종속 변수는 3 개 이상의 가능한 정렬 된 유형 또는 정량적 유의성을 갖는 유형을 가질 수 있습니다. 예를 들어, 이러한 변수는 "나쁨"또는 "좋음", "매우 좋음", "우수"를 나타낼 수 있으며 각 범주는 0,1,2,3과 같은 점수를 가질 수 있습니다.

로지스틱 회귀 가정

로지스틱 회귀를 구현하기 전에 다음과 같은 가정을 알고 있어야합니다.

• 이진 로지스틱 회귀의 경우 목표 변수는 항상 이진이어야하며 원하는 결과는 요인 수준 1로 표시됩니다.

• 모델에 다중 공선 성이 없어야합니다. 즉, 독립 변수가 서로 독립적이어야합니다.

• 모델에 의미있는 변수를 포함해야합니다.

• 로지스틱 회귀 분석을 위해 큰 표본 크기를 선택해야합니다.

이진 로지스틱 회귀 모델

로지스틱 회귀의 가장 간단한 형태는 이항 또는 이항 로지스틱 회귀입니다. 여기서 목표 또는 종속 변수는 1 또는 0의 두 가지 가능한 유형 만 가질 수 있습니다. 여러 예측 변수와 이항 / 이항 목표 변수 간의 관계를 모델링 할 수 있습니다. 로지스틱 회귀의 경우 선형 함수는 기본적으로 다음 관계와 같이 다른 함수에 대한 입력으로 사용됩니다.

$$ h _ {\ theta} {(x)} = g (\ theta ^ {T} x) ℎ 0≤h _ {\ theta} ≤1 $$

여기에 다음과 같이 주어질 수있는 로지스틱 또는 시그 모이 드 함수가 있습니다.

$$ g (z) = \ frac {1} {1 + e ^ {-z}} ℎ = \ theta ^ {T} $$

시그 모이 드 곡선은 다음 그래프의 도움으로 나타낼 수 있습니다. y 축 값이 0과 1 사이에 있고 0.5에서 축과 교차하는 것을 볼 수 있습니다.

클래스는 긍정 또는 부정으로 나눌 수 있습니다. 출력은 0과 1 사이에 있으면 양성 클래스 확률에 속합니다. 구현을 위해 가설 함수의 출력이 ≥0.5이면 양수로 해석하고 그렇지 않으면 음수로 해석합니다.

또한 다음과 같이 theta로 표현되는 함수에 대한 가중치를 사용하여 알고리즘이 얼마나 잘 수행되는지 측정하기 위해 손실 함수를 정의해야합니다.

ℎ = ()

$$ J (\ theta) = \ frac {1} {m}. (-y ^ {T} log (h)-(1 -y) ^ Tlog (1-h)) $$

이제 손실 함수를 정의한 후 우리의 주요 목표는 손실 함수를 최소화하는 것입니다. 가중치를 늘리거나 줄임으로써 가중치를 맞추는 방법으로 수행 할 수 있습니다. 각 가중치에 대한 손실 함수의 도함수를 사용하면 어떤 매개 변수가 높은 가중치를 가져야하고 어떤 매개 변수가 더 작은 가중치를 가져야하는지 알 수 있습니다.

다음 경사 하강 법 방정식은 매개 변수를 수정하면 손실이 어떻게 변하는 지 알려줍니다.

$$ \ frac {()} {\ theta_ {j}} = \ frac {1} {m} X ^ {T} (() −) $$

Python으로 구현

이제 위의 이항 로지스틱 회귀 개념을 파이썬으로 구현할 것입니다. 이를 위해 각각 50 개의 인스턴스로 구성된 3 개의 클래스가있는 'iris'라는 이름의 다변량 꽃 데이터 세트를 사용하지만 처음 두 개의 특성 열을 사용합니다. 모든 클래스는 붓꽃의 한 종류를 나타냅니다.

먼저 다음과 같이 필요한 라이브러리를 가져와야합니다.

import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn import datasets

다음으로 홍채 데이터 셋을 다음과 같이 불러옵니다.

iris = datasets.load_iris()
X = iris.data[:, :2]
y = (iris.target != 0) * 1

훈련 데이터를 다음과 같이 플롯 할 수 있습니다.

plt.figure(figsize=(6, 6))
plt.scatter(X[y == 0][:, 0], X[y == 0][:, 1], color='g', label='0')
plt.scatter(X[y == 1][:, 0], X[y == 1][:, 1], color='y', label='1')
plt.legend();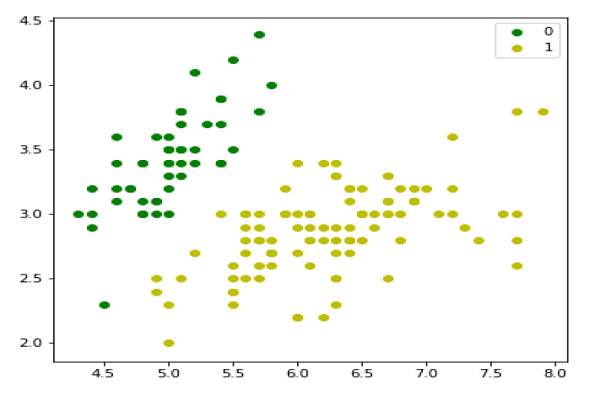

다음으로 시그 모이 드 함수, 손실 함수 및 기울기 하강을 다음과 같이 정의합니다.

class LogisticRegression:
   def __init__(self, lr=0.01, num_iter=100000, fit_intercept=True, verbose=False):
      self.lr = lr
      self.num_iter = num_iter
      self.fit_intercept = fit_intercept
      self.verbose = verbose
   def __add_intercept(self, X):
      intercept = np.ones((X.shape[0], 1))
      return np.concatenate((intercept, X), axis=1)
   def __sigmoid(self, z):
      return 1 / (1 + np.exp(-z))
   def __loss(self, h, y):
      return (-y * np.log(h) - (1 - y) * np.log(1 - h)).mean()
   def fit(self, X, y):
      if self.fit_intercept:
         X = self.__add_intercept(X)

이제 다음과 같이 가중치를 초기화하십시오.

self.theta = np.zeros(X.shape[1])
   for i in range(self.num_iter):
      z = np.dot(X, self.theta)
      h = self.__sigmoid(z)
      gradient = np.dot(X.T, (h - y)) / y.size
      self.theta -= self.lr * gradient
      z = np.dot(X, self.theta)
      h = self.__sigmoid(z)
      loss = self.__loss(h, y)
      if(self.verbose ==True and i % 10000 == 0):
         print(f'loss: {loss} \t')

다음 스크립트의 도움으로 출력 확률을 예측할 수 있습니다.

def predict_prob(self, X):
   if self.fit_intercept:
      X = self.__add_intercept(X)
   return self.__sigmoid(np.dot(X, self.theta))
def predict(self, X):
   return self.predict_prob(X).round()

다음으로 모델을 평가하고 다음과 같이 플로팅 할 수 있습니다.

model = LogisticRegression(lr=0.1, num_iter=300000)
preds = model.predict(X)
(preds == y).mean()

plt.figure(figsize=(10, 6))
plt.scatter(X[y == 0][:, 0], X[y == 0][:, 1], color='g', label='0')
plt.scatter(X[y == 1][:, 0], X[y == 1][:, 1], color='y', label='1')
plt.legend()
x1_min, x1_max = X[:,0].min(), X[:,0].max(),
x2_min, x2_max = X[:,1].min(), X[:,1].max(),
xx1, xx2 = np.meshgrid(np.linspace(x1_min, x1_max), np.linspace(x2_min, x2_max))
grid = np.c_[xx1.ravel(), xx2.ravel()]
probs = model.predict_prob(grid).reshape(xx1.shape)
plt.contour(xx1, xx2, probs, [0.5], linewidths=1, colors='red');

다항 로지스틱 회귀 모델

로지스틱 회귀의 또 다른 유용한 형태는 다항 로지스틱 회귀로, 대상 또는 종속 변수가 3 개 이상의 가능한 비 순차 유형, 즉 양적 유의성이없는 유형을 가질 수 있습니다.

Python으로 구현

이제 위의 다항 로지스틱 회귀 개념을 파이썬으로 구현할 것입니다. 이를 위해 digit라는 sklearn의 데이터 세트를 사용합니다.

먼저 다음과 같이 필요한 라이브러리를 가져와야합니다.

Import sklearn
from sklearn import datasets
from sklearn import linear_model
from sklearn import metrics
from sklearn.model_selection import train_test_split

다음으로 숫자 데이터 세트를로드해야합니다.

digits = datasets.load_digits()

이제 다음과 같이 특성 행렬 (X)과 응답 벡터 (y)를 정의합니다.

X = digits.data
y = digits.target

다음 코드 줄의 도움으로 X와 y를 훈련 및 테스트 세트로 나눌 수 있습니다.

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4, random_state=1)

이제 다음과 같이 로지스틱 회귀 객체를 만듭니다.

digreg = linear_model.LogisticRegression()

이제 다음과 같이 훈련 세트를 사용하여 모델을 훈련해야합니다.

digreg.fit(X_train, y_train)

다음으로 테스트 세트에 대한 예측을 다음과 같이 작성하십시오.

y_pred = digreg.predict(X_test)

다음으로 모델의 정확도를 다음과 같이 인쇄하십시오-

print("Accuracy of Logistic Regression model is:",
metrics.accuracy_score(y_test, y_pred)*100)

산출

Accuracy of Logistic Regression model is: 95.6884561891516

위의 결과에서 모델의 정확도가 약 96 %임을 알 수 있습니다.