클러스터링 알고리즘-계층 적 클러스터링

계층 적 클러스터링 소개

계층 적 클러스터링은 유사한 특성을 가진 레이블이없는 데이터 포인트를 함께 그룹화하는 데 사용되는 또 다른 비지도 학습 알고리즘입니다. 계층 적 클러스터링 알고리즘은 다음 두 가지 범주로 나뉩니다.

Agglomerative hierarchical algorithms− 통합 계층 알고리즘에서 각 데이터 포인트는 단일 클러스터로 처리 된 다음 클러스터 쌍을 연속적으로 병합하거나 통합합니다 (상향식 접근 방식). 군집의 계층은 덴드로 그램 또는 트리 구조로 표시됩니다.

Divisive hierarchical algorithms − 반면에 분할 계층 알고리즘에서는 모든 데이터 포인트가 하나의 큰 클러스터로 취급되고 클러스터링 프로세스에는 하나의 큰 클러스터를 다양한 작은 클러스터로 나누는 (하향식 접근 방식)이 포함됩니다.

집계 계층 적 클러스터링을 수행하는 단계

우리는 가장 많이 사용되고 중요한 계층 적 클러스터링, 즉 응집에 대해 설명 할 것입니다. 동일한 작업을 수행하는 단계는 다음과 같습니다.

Step 1− 각 데이터 포인트를 단일 클러스터로 취급합니다. 따라서 우리는 처음에 K 클러스터를 갖게 될 것입니다. 데이터 포인트의 수도 시작시 K가됩니다.
Step 2− 이제이 단계에서 두 개의 closet 데이터 포인트를 결합하여 큰 클러스터를 형성해야합니다. 이로 인해 총 K-1 클러스터가 생성됩니다.
Step 3− 이제 더 많은 클러스터를 형성하려면 두 개의 옷장 클러스터를 결합해야합니다. 이렇게하면 총 K-2 클러스터가 생성됩니다.
Step 4 -이제 하나의 큰 클러스터를 형성하려면 K가 0이 될 때까지 위의 세 단계를 반복합니다. 즉, 결합 할 데이터 포인트가 더 이상 남지 않습니다.
Step 5 -마지막으로 하나의 큰 클러스터를 만든 후 덴드로 그램을 사용하여 문제에 따라 여러 클러스터로 나눕니다.

Agglomerative Hierarchical Clustering에서 Dendrograms의 역할

마지막 단계에서 논의했듯이 덴드로 그램의 역할은 큰 클러스터가 형성되면 시작됩니다. 덴드로 그램은 문제에 따라 클러스터를 관련 데이터 포인트의 여러 클러스터로 분할하는 데 사용됩니다. 다음 예제의 도움으로 이해할 수 있습니다-

예 1

이해하기 위해 다음과 같이 필요한 라이브러리를 가져 오는 것으로 시작하겠습니다.

%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np

다음으로,이 예제에서 가져온 데이터 포인트를 플로팅 할 것입니다.

X = np.array([[7,8],[12,20],[17,19],[26,15],[32,37],[87,75],[73,85], [62,80],[73,60],[87,96],])
labels = range(1, 11)
plt.figure(figsize=(10, 7))
plt.subplots_adjust(bottom=0.1)
plt.scatter(X[:,0],X[:,1], label='True Position')
for label, x, y in zip(labels, X[:, 0], X[:, 1]):
   plt.annotate(label,xy=(x, y), xytext=(-3, 3),textcoords='offset points', ha='right', va='bottom')
plt.show()

위의 다이어그램에서 아웃 데이터 포인트에 두 개의 클러스터가 있음을 매우 쉽게 알 수 있지만 실제 데이터에는 수천 개의 클러스터가있을 수 있습니다. 다음으로 Scipy 라이브러리를 사용하여 데이터 포인트의 덴드로 그램을 플로팅합니다.

from scipy.cluster.hierarchy import dendrogram, linkage
from matplotlib import pyplot as plt
linked = linkage(X, 'single')
labelList = range(1, 11)
plt.figure(figsize=(10, 7))
dendrogram(linked, orientation='top',labels=labelList, distance_sort='descending',show_leaf_counts=True)
plt.show()

이제 큰 클러스터가 형성되면 가장 긴 수직 거리가 선택됩니다. 그러면 다음 다이어그램과 같이 수직선이 그려집니다. 수평선이 두 지점에서 파란색 선을 가로 지르면 클러스터 수는 2 개가됩니다.

다음으로, 클러스터링을 위해 클래스를 가져오고 fit_predict 메서드를 호출하여 클러스터를 예측해야합니다. sklearn.cluster 라이브러리의 AgglomerativeClustering 클래스를 가져옵니다.

from sklearn.cluster import AgglomerativeClustering
cluster = AgglomerativeClustering(n_clusters=2, affinity='euclidean', linkage='ward')
cluster.fit_predict(X)

다음으로 다음 코드를 사용하여 클러스터를 플로팅합니다.

plt.scatter(X[:,0],X[:,1], c=cluster.labels_, cmap='rainbow')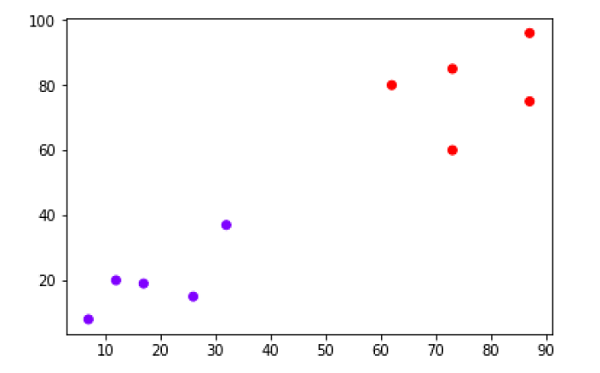

위의 다이어그램은 데이터 포인트의 두 클러스터를 보여줍니다.

예 2

위에서 설명한 간단한 예에서 덴드로 그램의 개념을 이해 했으므로 계층 적 클러스터링을 사용하여 Pima Indian Diabetes Dataset에서 데이터 포인트의 클러스터를 만드는 다른 예로 이동하겠습니다.

import matplotlib.pyplot as plt
import pandas as pd
%matplotlib inline
import numpy as np
from pandas import read_csv
path = r"C:\pima-indians-diabetes.csv"
headernames = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=headernames)
array = data.values
X = array[:,0:8]
Y = array[:,8]
data.shape
(768, 9)
data.head()

slno.	preg	Plas	대가	피부	테스트	질량	페디	나이	수업
0	6	148	72	35	0	33.6	0.627	50	1
1	1	85	66	29	0	26.6	0.351	31	0
2	8	183	64	0	0	23.3	0.672	32	1
삼	1	89	66	23	94	28.1	0.167	21	0
4	0	137	40	35	168	43.1	2.288	33	1

patient_data = data.iloc[:, 3:5].values
import scipy.cluster.hierarchy as shc
plt.figure(figsize=(10, 7))
plt.title("Patient Dendograms")
dend = shc.dendrogram(shc.linkage(data, method='ward'))

from sklearn.cluster import AgglomerativeClustering
cluster = AgglomerativeClustering(n_clusters=4, affinity='euclidean', linkage='ward')
cluster.fit_predict(patient_data)
plt.figure(figsize=(10, 7))
plt.scatter(patient_data[:,0], patient_data[:,1], c=cluster.labels_, cmap='rainbow')