회귀 알고리즘-선형 회귀

선형 회귀 소개

선형 회귀는 주어진 독립 변수 집합을 사용하여 종속 변수 간의 선형 관계를 분석하는 통계 모델로 정의 할 수 있습니다. 변수 간의 선형 관계는 하나 이상의 독립 변수의 값이 변경 (증가 또는 감소) 될 때 종속 변수의 값도 그에 따라 변경 (증가 또는 감소)됨을 의미합니다.

수학적으로 관계는 다음 방정식의 도움으로 나타낼 수 있습니다.

Y = mX + b

여기서 Y는 예측하려는 종속 변수입니다.

X 는 예측을 위해 사용하는 종속 변수입니다.

m 은 X가 Y에 미치는 영향을 나타내는 회귀선의 기울기입니다.

b 는 Y 절편이라고하는 상수입니다. X = 0이면 Y는 b와 같습니다.

또한 선형 관계는 아래에 설명 된대로 본질적으로 양수 또는 음수 일 수 있습니다.

양의 선형 관계

독립 변수와 종속 변수가 모두 증가하면 선형 관계를 양수라고합니다. 다음 그래프의 도움으로 이해할 수 있습니다-

음의 선형 관계

독립 변수가 증가하고 종속 변수가 감소하면 선형 관계를 양수라고합니다. 다음 그래프의 도움으로 이해할 수 있습니다-

선형 회귀 유형

선형 회귀는 다음 두 가지 유형입니다.

단순 선형 회귀
다중 선형 회귀

단순 선형 회귀 (SLR)

단일 기능을 사용하여 응답을 예측하는 가장 기본적인 선형 회귀 버전입니다. SLR의 가정은 두 변수가 선형 적으로 관련되어 있다는 것입니다.

Python 구현

Python에서 SLR을 두 가지 방법으로 구현할 수 있습니다. 하나는 자체 데이터 세트를 제공하는 것이고 다른 하나는 scikit-learn python 라이브러리의 데이터 세트를 사용하는 것입니다.

Example 1 − 다음 Python 구현 예제에서는 자체 데이터 세트를 사용하고 있습니다.

먼저 다음과 같이 필요한 패키지를 가져 오는 것으로 시작합니다.

%matplotlib inline
import numpy as np
import matplotlib.pyplot as plt

다음으로, SLR의 중요한 값을 계산할 함수를 정의하십시오.

def coef_estimation(x, y):

다음 스크립트 줄은 관찰 수 n을 제공합니다-

n = np.size(x)

x 및 y 벡터의 평균은 다음과 같이 계산할 수 있습니다.

m_x, m_y = np.mean(x), np.mean(y)

다음과 같이 x에 대한 교차 편차와 편차를 찾을 수 있습니다.

SS_xy = np.sum(y*x) - n*m_y*m_x
SS_xx = np.sum(x*x) - n*m_x*m_x

다음으로 회귀 계수 즉 b는 다음과 같이 계산할 수 있습니다.

b_1 = SS_xy / SS_xx
b_0 = m_y - b_1*m_x
return(b_0, b_1)

다음으로 회귀선을 플로팅하고 응답 벡터를 예측하는 함수를 정의해야합니다.

def plot_regression_line(x, y, b):

다음 스크립트 라인은 실제 포인트를 산점도로 플롯합니다.

plt.scatter(x, y, color = "m", marker = "o", s = 30)

다음 스크립트 줄은 응답 벡터를 예측합니다.

y_pred = b[0] + b[1]*x

다음 스크립트 라인은 회귀선을 플로팅하고 레이블을 붙입니다.

plt.plot(x, y_pred, color = "g")
plt.xlabel('x')
plt.ylabel('y')
plt.show()

마지막으로 데이터 셋을 제공하고 위에서 정의한 함수를 호출하기 위해 main () 함수를 정의해야합니다.

def main():
   x = np.array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
   y = np.array([100, 300, 350, 500, 750, 800, 850, 900, 1050, 1250])
   b = coef_estimation(x, y)
   print("Estimated coefficients:\nb_0 = {} \nb_1 = {}".format(b[0], b[1]))
   plot_regression_line(x, y, b)
   
if __name__ == "__main__":
main()

산출

Estimated coefficients:
b_0 = 154.5454545454545
b_1 = 117.87878787878788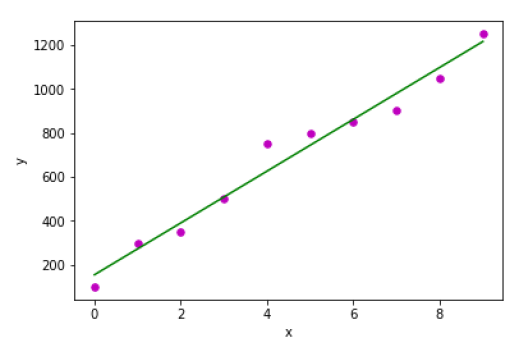

Example 2 − 다음 Python 구현 예제에서는 scikit-learn의 당뇨병 데이터 세트를 사용하고 있습니다.

먼저 다음과 같이 필요한 패키지를 가져 오는 것으로 시작합니다.

%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, linear_model
from sklearn.metrics import mean_squared_error, r2_score

다음으로 당뇨병 데이터 셋을로드하고 객체를 생성합니다.

diabetes = datasets.load_diabetes()

SLR을 구현할 때 다음과 같이 하나의 기능 만 사용합니다.

X = diabetes.data[:, np.newaxis, 2]

다음으로 데이터를 다음과 같이 훈련 및 테스트 세트로 분할해야합니다.

X_train = X[:-30]
X_test = X[-30:]

다음으로 목표를 다음과 같이 훈련 및 테스트 세트로 분할해야합니다.

y_train = diabetes.target[:-30]
y_test = diabetes.target[-30:]

이제 모델을 훈련하려면 다음과 같이 선형 회귀 객체를 만들어야합니다.

regr = linear_model.LinearRegression()

다음으로 다음과 같이 훈련 세트를 사용하여 모델을 훈련시킵니다.

regr.fit(X_train, y_train)

다음으로 테스트 세트를 사용하여 다음과 같이 예측하십시오.

y_pred = regr.predict(X_test)

다음으로 MSE, Variance score 등과 같은 계수를 다음과 같이 인쇄합니다.

print('Coefficients: \n', regr.coef_)
print("Mean squared error: %.2f" % mean_squared_error(y_test, y_pred))
print('Variance score: %.2f' % r2_score(y_test, y_pred))

이제 다음과 같이 출력을 플로팅합니다.

plt.scatter(X_test, y_test, color='blue')
plt.plot(X_test, y_pred, color='red', linewidth=3)
plt.xticks(())
plt.yticks(())
plt.show()

산출

Coefficients:
   [941.43097333]
Mean squared error: 3035.06
Variance score: 0.41

다중 선형 회귀 (MLR)

두 개 이상의 특성을 사용하여 반응을 예측하는 것은 단순 선형 회귀의 확장입니다. 수학적으로 다음과 같이 설명 할 수 있습니다.

n 개의 관측치, p 개의 특징, 즉 독립 변수와 y를 하나의 응답으로 가진 데이터 세트를 고려하십시오. 즉, p 특징에 대한 회귀선은 다음과 같이 계산 될 수 있습니다.

$$ h (x_ {i}) = b_ {0} + b_ {1} x_ {i1} + b_ {2} x_ {i2} + ... + b_ {p} x_ {ip} $$

여기서 h (x _i )는 예측 된 반응 값이고 b ₀ , b ₁ , b ₂ …, b _p 는 회귀 계수입니다.

다중 선형 회귀 모델은 항상 다음과 같이 계산을 변경하는 잔차 오류로 알려진 데이터의 오류를 포함합니다.

$$ h (x_ {i}) = b_ {0} + b_ {1} x_ {i1} + b_ {2} x_ {i2} + ... + b_ {p} x_ {ip} + e_ {i} $$

위의 방정식을 다음과 같이 쓸 수도 있습니다.

$$ y_ {i} = h (x_ {i}) + e_ {i} \ : 또는 \ : e_ {i} = y_ {i}-h (x_ {i}) $$

Python 구현

이 예에서는 scikit learn의 Boston 주택 데이터 세트를 사용합니다.

먼저 다음과 같이 필요한 패키지를 가져 오는 것으로 시작합니다.

%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, linear_model, metrics

다음으로 데이터 세트를 다음과 같이로드합니다.

boston = datasets.load_boston(return_X_y=False)

다음 스크립트 줄은 특성 행렬, X 및 응답 벡터, Y를 정의합니다.

X = boston.data
y = boston.target

다음으로 데이터 세트를 다음과 같이 훈련 및 테스트 세트로 분할합니다.

from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.7, random_state=1)

예

이제 선형 회귀 객체를 만들고 다음과 같이 모델을 훈련시킵니다.

reg = linear_model.LinearRegression()
reg.fit(X_train, y_train)
print('Coefficients: \n', reg.coef_)
print('Variance score: {}'.format(reg.score(X_test, y_test)))
plt.style.use('fivethirtyeight')
plt.scatter(reg.predict(X_train), reg.predict(X_train) - y_train,
   color = "green", s = 10, label = 'Train data')
plt.scatter(reg.predict(X_test), reg.predict(X_test) - y_test,
   color = "blue", s = 10, label = 'Test data')
plt.hlines(y = 0, xmin = 0, xmax = 50, linewidth = 2)
plt.legend(loc = 'upper right')
plt.title("Residual errors")
plt.show()

산출

Coefficients:
[
   -1.16358797e-01  6.44549228e-02  1.65416147e-01  1.45101654e+00
   -1.77862563e+01  2.80392779e+00  4.61905315e-02 -1.13518865e+00
    3.31725870e-01 -1.01196059e-02 -9.94812678e-01  9.18522056e-03
   -7.92395217e-01
]
Variance score: 0.709454060230326