MATLAB-미분

MATLAB은 diff기호 파생물을 계산하기위한 명령. 가장 간단한 형식으로 차별화하려는 함수를 diff 명령에 인수로 전달합니다.

예를 들어 함수 f (t) = 3t 2 + 2t -2 의 미분을 계산해 봅시다

예

스크립트 파일을 생성하고 다음 코드를 입력하십시오.

syms t
f = 3*t^2 + 2*t^(-2);
diff(f)

위의 코드가 컴파일되고 실행되면 다음과 같은 결과가 생성됩니다.

ans =
6*t - 4/t^3

다음은 위의 계산에 해당하는 옥타브입니다.

pkg load symbolic
symbols

t = sym("t");
f = 3*t^2 + 2*t^(-2);
differentiate(f,t)

Octave는 코드를 실행하고 다음 결과를 반환합니다.

ans =
   -(4.0)*t^(-3.0)+(6.0)*t

차별화의 기본 규칙 검증

함수의 미분을위한 다양한 방정식이나 규칙을 간단히 설명하고 이러한 규칙을 검증 해 보겠습니다. 이를 위해 1 차 미분에 대해 f '(x)를, 2 차 미분에 대해 f "(x)를 작성합니다.

다음은 차별화를위한 규칙입니다.

규칙 1

모든 함수 f와 g와 실수 a와 b는 함수의 미분입니다.

h(x) = af(x) + bg(x) x와 관련하여-

h'(x) = af'(x) + bg'(x)

규칙 2

그만큼 sum 과 subtraction 규칙에 따르면 f와 g가 두 함수 인 경우 f '와 g'는 각각 도함수입니다.

(f + g)' = f' + g'

(f - g)' = f' - g'

규칙 3

그만큼 product 규칙에 따르면 f와 g가 두 함수 인 경우 f '와 g'는 각각 파생 된 것입니다.

(f.g)' = f'.g + g'.f

규칙 4

그만큼 quotient 규칙에 따르면 f와 g가 두 함수 인 경우 f '와 g'는 각각 파생 된 것입니다.

(f/g)' = (f'.g - g'.f)/g2

규칙 5

그만큼 polynomial 또는 기본 전원 규칙에 따르면 y = f(x) = xn, 다음 f' = n. x(n-1)

이 규칙의 직접적인 결과는 상수의 미분이 0이라는 것입니다. y = k, 임의의 상수,

f' = 0

규칙 6

그만큼 chain 규칙은 함수의 기능의 미분 h(x) = f(g(x)) x와 관련하여

h'(x)= f'(g(x)).g'(x)

예

스크립트 파일을 생성하고 다음 코드를 입력하십시오.

syms x
syms t

f = (x + 2)*(x^2 + 3)
der1 = diff(f)

f = (t^2 + 3)*(sqrt(t) + t^3)
der2 = diff(f)

f = (x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2)
der3 = diff(f)

f = (2*x^2 + 3*x)/(x^3 + 1)
der4 = diff(f)

f = (x^2 + 1)^17
der5 = diff(f)

f = (t^3 + 3* t^2 + 5*t -9)^(-6)
der6 = diff(f)

파일을 실행하면 MATLAB은 다음 결과를 표시합니다.

f =
   (x^2 + 3)*(x + 2)
 
   der1 =
   2*x*(x + 2) + x^2 + 3
  
f =
   (t^(1/2) + t^3)*(t^2 + 3)
 
   der2 =
   (t^2 + 3)*(3*t^2 + 1/(2*t^(1/2))) + 2*t*(t^(1/2) + t^3)
  
f =
   (x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2)
  
der3 =
   (2*x - 2)*(3*x^3 - 5*x^2 + 2) - (- 9*x^2 + 10*x)*(x^2 - 2*x + 1)
 
f =
   (2*x^2 + 3*x)/(x^3 + 1)
  
der4 =
   (4*x + 3)/(x^3 + 1) - (3*x^2*(2*x^2 + 3*x))/(x^3 + 1)^2
  
f =
   (x^2 + 1)^17
  
der5 =
   34*x*(x^2 + 1)^16
  
f =
   1/(t^3 + 3*t^2 + 5*t - 9)^6
  
der6 =
   -(6*(3*t^2 + 6*t + 5))/(t^3 + 3*t^2 + 5*t - 9)^7

다음은 위의 계산에 해당하는 옥타브입니다.

pkg load symbolic
symbols

x = sym("x");
t = sym("t");

f = (x + 2)*(x^2 + 3) 
der1 = differentiate(f,x) 

f = (t^2 + 3)*(t^(1/2) + t^3) 
der2 = differentiate(f,t) 

f = (x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2) 
der3 = differentiate(f,x) 

f = (2*x^2 + 3*x)/(x^3 + 1) 
der4 = differentiate(f,x) 

f = (x^2 + 1)^17 
der5 = differentiate(f,x) 

f = (t^3 + 3* t^2 + 5*t -9)^(-6) 
der6 = differentiate(f,t)

Octave는 코드를 실행하고 다음 결과를 반환합니다.

f =

(2.0+x)*(3.0+x^(2.0))
der1 =

3.0+x^(2.0)+(2.0)*(2.0+x)*x
f =

(t^(3.0)+sqrt(t))*(3.0+t^(2.0))
der2 =

(2.0)*(t^(3.0)+sqrt(t))*t+((3.0)*t^(2.0)+(0.5)*t^(-0.5))*(3.0+t^(2.0))
f =

(1.0+x^(2.0)-(2.0)*x)*(2.0-(5.0)*x^(2.0)+(3.0)*x^(3.0))
der3 =

(-2.0+(2.0)*x)*(2.0-(5.0)*x^(2.0)+(3.0)*x^(3.0))+((9.0)*x^(2.0)-(10.0)*x)*(1.0+x^(2.0)-(2.0)*x)
f =

(1.0+x^(3.0))^(-1)*((2.0)*x^(2.0)+(3.0)*x)
der4 =

(1.0+x^(3.0))^(-1)*(3.0+(4.0)*x)-(3.0)*(1.0+x^(3.0))^(-2)*x^(2.0)*((2.0)*x^(2.0)+(3.0)*x)
f =

(1.0+x^(2.0))^(17.0)
der5 =

(34.0)*(1.0+x^(2.0))^(16.0)*x
f =

(-9.0+(3.0)*t^(2.0)+t^(3.0)+(5.0)*t)^(-6.0)
der6 =

-(6.0)*(-9.0+(3.0)*t^(2.0)+t^(3.0)+(5.0)*t)^(-7.0)*(5.0+(3.0)*t^(2.0)+(6.0)*t)

지수, 로그 및 삼각 함수의 미분

다음 표는 일반적으로 사용되는 지수, 로그 및 삼각 함수의 미분을 제공합니다.

함수 유도체
ca.x c a.x .ln ca (ln은 자연 로그)
ex e x
ln x 1 / x
lncx 1 / x.ln c
xx x x . (1 + ln x)
sin(x) cos (x)
cos(x) -죄 (x)
tan(x) sec 2 (x) 또는 1 / cos 2 (x) 또는 1 + tan 2 (x)
cot(x) -csc 2 (x) 또는 -1 / sin 2 (x) 또는-(1 + cot 2 (x))
sec(x) 초 (x) .tan (x)
csc(x) -csc (x) .cot (x)

예

스크립트 파일을 생성하고 다음 코드를 입력하십시오.

syms x
y = exp(x)
diff(y)

y = x^9
diff(y)

y = sin(x)
diff(y)

y = tan(x)
diff(y)

y = cos(x)
diff(y)

y = log(x)
diff(y)

y = log10(x)
diff(y)

y = sin(x)^2
diff(y)

y = cos(3*x^2 + 2*x + 1)
diff(y)

y = exp(x)/sin(x)
diff(y)

파일을 실행하면 MATLAB은 다음 결과를 표시합니다.

y =
   exp(x)
   ans =
   exp(x)

y =
   x^9
   ans =
   9*x^8
  
y =
   sin(x)
   ans =
   cos(x)
  
y =
   tan(x)
   ans =
   tan(x)^2 + 1
 
y =
   cos(x)
   ans =
   -sin(x)
  
y =
   log(x)
   ans =
   1/x
  
y =
   log(x)/log(10)
   ans =
   1/(x*log(10))
 
y =
   sin(x)^2
   ans =
   2*cos(x)*sin(x)
 
y =
   cos(3*x^2 + 2*x + 1)
   ans =
   -sin(3*x^2 + 2*x + 1)*(6*x + 2)
  
y =
   exp(x)/sin(x)
   ans =
   exp(x)/sin(x) - (exp(x)*cos(x))/sin(x)^2

다음은 위의 계산에 해당하는 옥타브입니다.

pkg load symbolic
symbols

x = sym("x");
y = Exp(x)
differentiate(y,x)

y = x^9
differentiate(y,x)

y = Sin(x)
differentiate(y,x)

y = Tan(x)
differentiate(y,x)

y = Cos(x)
differentiate(y,x)

y = Log(x)
differentiate(y,x)

% symbolic packages does not have this support
%y = Log10(x)
%differentiate(y,x)

y = Sin(x)^2
differentiate(y,x)

y = Cos(3*x^2 + 2*x + 1)
differentiate(y,x)

y = Exp(x)/Sin(x)
differentiate(y,x)

Octave는 코드를 실행하고 다음 결과를 반환합니다.

y =

exp(x)
ans =

exp(x)
y =

x^(9.0)
ans =

(9.0)*x^(8.0)
y =

sin(x)
ans =

cos(x)
y =

tan(x)
ans =

1+tan(x)^2
y =

cos(x)
ans =

-sin(x)
y =

log(x)
ans =

x^(-1)
y =

sin(x)^(2.0)
ans =

(2.0)*sin(x)*cos(x)
y =

cos(1.0+(2.0)*x+(3.0)*x^(2.0))
ans =

-(2.0+(6.0)*x)*sin(1.0+(2.0)*x+(3.0)*x^(2.0))
y =

sin(x)^(-1)*exp(x)
ans =

sin(x)^(-1)*exp(x)-sin(x)^(-2)*cos(x)*exp(x)

고차 파생물 계산

함수 f의 더 높은 도함수를 계산하기 위해 다음 구문을 사용합니다. diff(f,n).

함수 y = f (x) = x .e -3x 의 2 차 도함수를 계산해 봅시다.

f = x*exp(-3*x);
diff(f, 2)

MATLAB은 코드를 실행하고 다음 결과를 반환합니다.

ans =
9*x*exp(-3*x) - 6*exp(-3*x)

다음은 위의 계산에 해당하는 옥타브입니다.

pkg load symbolic
symbols

x = sym("x");
f = x*Exp(-3*x);
differentiate(f, x, 2)

Octave는 코드를 실행하고 다음 결과를 반환합니다.

ans =

(9.0)*exp(-(3.0)*x)*x-(6.0)*exp(-(3.0)*x)

예

이 예에서는 문제를 해결해 보겠습니다. 그 기능을 감안할 때y = f(x) = 3 sin(x) + 7 cos(5x). 우리는 방정식이f" + f = -5cos(2x) 사실입니다.

스크립트 파일을 생성하고 다음 코드를 입력하십시오.

syms x
y = 3*sin(x)+7*cos(5*x);  % defining the function
lhs = diff(y,2)+y;        %evaluting the lhs of the equation
rhs = -5*cos(2*x);        %rhs of the equation
if(isequal(lhs,rhs))
   disp('Yes, the equation holds true');
else
   disp('No, the equation does not hold true');
end
disp('Value of LHS is: '), disp(lhs);

파일을 실행하면 다음 결과가 표시됩니다.

No, the equation does not hold true
Value of LHS is: 
-168*cos(5*x)

다음은 위의 계산에 해당하는 옥타브입니다.

pkg load symbolic
symbols

x = sym("x");
y = 3*Sin(x)+7*Cos(5*x);           % defining the function
lhs = differentiate(y, x, 2) + y;  %evaluting the lhs of the equation
rhs = -5*Cos(2*x);                 %rhs of the equation

if(lhs == rhs)
   disp('Yes, the equation holds true');
else
   disp('No, the equation does not hold true');
end
disp('Value of LHS is: '), disp(lhs);

Octave는 코드를 실행하고 다음 결과를 반환합니다.

No, the equation does not hold true
Value of LHS is: 
-(168.0)*cos((5.0)*x)

곡선의 최대 값과 최소값 찾기

그래프에 대한 로컬 최대 값과 최소값을 검색하는 경우 기본적으로 특정 지역에서 함수 그래프의 최고 또는 최저 지점 또는 기호 변수의 특정 값 범위를 찾습니다.

함수 y = f (x)의 경우 그래프에서 기울기가 0 인 지점이 호출됩니다. stationary points. 즉, 고정 점은 f '(x) = 0입니다.

미분하는 함수의 고정 점을 찾으려면 미분을 0으로 설정하고 방정식을 풀어야합니다.

예

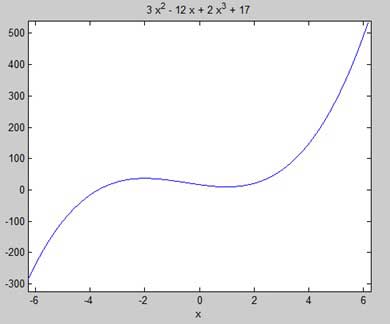
함수 f (x) = 2x 3 + 3x 2 − 12x + 17 의 고정 점을 찾아 봅시다.

다음 단계를 수행하십시오-

First let us enter the function and plot its graph.

syms x
y = 2*x^3 + 3*x^2 - 12*x + 17;   % defining the function
ezplot(y)

MATLAB은 코드를 실행하고 다음 플롯을 반환합니다.

다음은 위의 예에 대한 Octave에 해당하는 코드입니다.

pkg load symbolic
symbols

x = sym('x');
y = inline("2*x^3 + 3*x^2 - 12*x + 17");

ezplot(y)
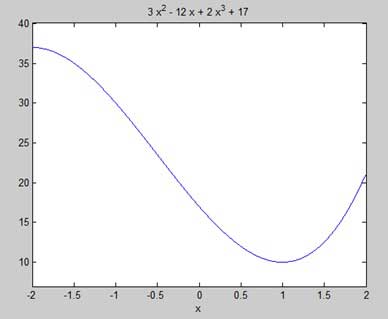
print -deps graph.eps

Our aim is to find some local maxima and minima on the graph, so let us find the local maxima and minima for the interval [-2, 2] on the graph.

syms x
y = 2*x^3 + 3*x^2 - 12*x + 17;   % defining the function
ezplot(y, [-2, 2])

MATLAB은 코드를 실행하고 다음 플롯을 반환합니다.

다음은 위의 예에 대한 Octave에 해당하는 코드입니다.

pkg load symbolic
symbols

x = sym('x');
y = inline("2*x^3 + 3*x^2 - 12*x + 17");

ezplot(y, [-2, 2])
print -deps graph.eps

Next, let us compute the derivative.

g = diff(y)

MATLAB은 코드를 실행하고 다음 결과를 반환합니다.

g =
   6*x^2 + 6*x - 12

다음은 위의 계산에 해당하는 옥타브입니다.

pkg load symbolic
symbols

x = sym("x");
y = 2*x^3 + 3*x^2 - 12*x + 17;
g = differentiate(y,x)

Octave는 코드를 실행하고 다음 결과를 반환합니다.

g =
   -12.0+(6.0)*x+(6.0)*x^(2.0)

Let us solve the derivative function, g, to get the values where it becomes zero.

s = solve(g)

MATLAB은 코드를 실행하고 다음 결과를 반환합니다.

s =
   1
   -2

다음은 위의 계산에 해당하는 옥타브입니다.

pkg load symbolic
symbols

x = sym("x");
y = 2*x^3 + 3*x^2 - 12*x + 17;
g = differentiate(y,x)
roots([6, 6, -12])

Octave는 코드를 실행하고 다음 결과를 반환합니다.

g =

-12.0+(6.0)*x^(2.0)+(6.0)*x
ans =

  -2
   1

This agrees with our plot. So let us evaluate the function f at the critical points x = 1, -2. 기호 함수의 값을 다음을 사용하여 대체 할 수 있습니다. subs 명령.

subs(y, 1), subs(y, -2)

MATLAB은 코드를 실행하고 다음 결과를 반환합니다.

ans =
   10
ans =
   37

다음은 위의 계산에 해당하는 옥타브입니다.

pkg load symbolic
symbols

x = sym("x");
y = 2*x^3 + 3*x^2 - 12*x + 17;
g = differentiate(y,x)

roots([6, 6, -12])
subs(y, x, 1), subs(y, x, -2)

ans =
   10.0
ans =
   37.0-4.6734207789940138748E-18*I

따라서 구간 [-2,2] 에서 함수 f (x) = 2x 3 + 3x 2 − 12x + 17 의 최소값과 최대 값 은 10과 37입니다.

미분 방정식 풀기

MATLAB은 dsolve 미분 방정식을 상징적으로 풀기위한 명령.

가장 기본적인 형태는 dsolve 단일 방정식에 대한 해를 찾는 명령은 다음과 같습니다.

dsolve('eqn')

여기서 eqn 은 방정식을 입력하는 데 사용되는 텍스트 문자열입니다.

MATLAB이 C1, C2 등의 레이블을 지정하는 임의의 상수 집합이있는 기호 솔루션을 반환합니다.

방정식 다음에 쉼표로 구분 된 목록으로 문제에 대한 초기 및 경계 조건을 지정할 수도 있습니다.

dsolve('eqn','cond1', 'cond2',…)

dsolve 명령을 사용하기 위해 derivatives are indicated with a D. 예를 들어 f '(t) = -2 * f + cost (t)와 같은 방정식은 −

'Df = -2*f + cos(t)'

더 높은 도함수는 도함수의 순서에 따라 D 다음에 표시됩니다.

예를 들어 방정식 f "(x) + 2f '(x) = 5sin3x는 다음과 같이 입력해야합니다.

'D2y + 2Dy = 5*sin(3*x)'

1 차 미분 방정식의 간단한 예를 들어 보겠습니다 : y '= 5y.

s = dsolve('Dy = 5*y')

MATLAB은 코드를 실행하고 다음 결과를 반환합니다.

s =
   C2*exp(5*t)

2 차 미분 방정식의 또 다른 예를 살펴 보겠습니다. y "-y = 0, y (0) = -1, y '(0) = 2

dsolve('D2y - y = 0','y(0) = -1','Dy(0) = 2')

MATLAB은 코드를 실행하고 다음 결과를 반환합니다.

ans =
   exp(t)/2 - (3*exp(-t))/2
ja/tutorial
es/tutorial
de/tutorial
fr/tutorial
th/tutorial
pt/tutorial
ru/tutorial
vi/tutorial
it/tutorial
ko/tutorial
tr/tutorial
id/tutorial
pl/tutorial
hi/tutorial
japost
espost
depost
frpost
thpost
ptpost
rupost
vipost
itpost
kopost
trpost
idpost
plpost
hipost

© Copyright 2021 - 2024 | All Rights Reserved