MATLAB-통합
통합은 본질적으로 다른 두 가지 유형의 문제를 다룹니다.
첫 번째 유형에서는 함수의 미분이 주어지고 함수를 찾고 싶습니다. 따라서 우리는 기본적으로 차별화 과정을 역전시킵니다. 이 역 과정은 반 분화, 원시 함수 찾기 또는indefinite integral.
두 번째 유형의 문제는 매우 많은 수의 매우 작은 수량을 더한 다음 수량의 크기가 0에 가까워지면 제한을받는 반면 항의 수는 무한대에 가깝습니다. 이 과정은definite integral.
한정 적분은 면적, 부피, 무게 중심, 관성 모멘트, 힘에 의해 수행되는 작업 및 기타 여러 응용 분야를 찾는 데 사용됩니다.
MATLAB을 사용하여 부정적분 찾기
정의에 따라 함수 f (x)의 미분이 f '(x)이면 x에 대한 f'(x)의 부정적분은 f (x)라고 말합니다. 예를 들어 x 2 의 미분 (x에 대한) 이 2x이므로 2x의 부정적분은 x 2 라고 말할 수 있습니다 .
기호에서-
f'(x2) = 2x따라서
∫ 2xdx = x2.
정수 c의 값에 대한 x 2 + c의 미분도 2x이기 때문에 부정적분은 고유하지 않습니다 .
이것은 기호로 표현됩니다-
∫ 2xdx = x2 + c.
여기서 c는 '임의 상수'라고합니다.
MATLAB은 int식의 적분을 계산하는 명령입니다. 함수의 부정적분에 대한 표현식을 유도하기 위해 다음과 같이 작성합니다.
int(f);예를 들어, 이전 예에서-
syms x
int(2*x)MATLAB은 위의 문을 실행하고 다음 결과를 반환합니다.
ans =
x^2예 1
이 예에서는 일반적으로 사용되는 일부 식의 적분을 찾아 보겠습니다. 스크립트 파일을 만들고 그 안에 다음 코드를 입력하십시오-
syms x n
int(sym(x^n))
f = 'sin(n*t)'
int(sym(f))
syms a t
int(a*cos(pi*t))
int(a^x)파일을 실행하면 다음 결과가 표시됩니다.
ans =
piecewise([n == -1, log(x)], [n ~= -1, x^(n + 1)/(n + 1)])
f =
sin(n*t)
ans =
-cos(n*t)/n
ans =
(a*sin(pi*t))/pi
ans =
a^x/log(a)예 2
스크립트 파일을 만들고 그 안에 다음 코드를 입력하십시오-
syms x n
int(cos(x))
int(exp(x))
int(log(x))
int(x^-1)
int(x^5*cos(5*x))
pretty(int(x^5*cos(5*x)))
int(x^-5)
int(sec(x)^2)
pretty(int(1 - 10*x + 9 * x^2))
int((3 + 5*x -6*x^2 - 7*x^3)/2*x^2)
pretty(int((3 + 5*x -6*x^2 - 7*x^3)/2*x^2))참고 pretty 함수는 더 읽기 쉬운 형식으로 표현식을 반환합니다.
파일을 실행하면 다음 결과가 표시됩니다.
ans =
sin(x)
ans =
exp(x)
ans =
x*(log(x) - 1)
ans =
log(x)
ans =
(24*cos(5*x))/3125 + (24*x*sin(5*x))/625 - (12*x^2*cos(5*x))/125 + (x^4*cos(5*x))/5 - (4*x^3*sin(5*x))/25 + (x^5*sin(5*x))/5
2 4
24 cos(5 x) 24 x sin(5 x) 12 x cos(5 x) x cos(5 x)
----------- + ------------- - -------------- + ------------
3125 625 125 5
3 5
4 x sin(5 x) x sin(5 x)
------------- + -----------
25 5
ans =
-1/(4*x^4)
ans =
tan(x)
2
x (3 x - 5 x + 1)
ans =
- (7*x^6)/12 - (3*x^5)/5 + (5*x^4)/8 + x^3/2
6 5 4 3
7 x 3 x 5 x x
- ---- - ---- + ---- + --
12 5 8 2MATLAB을 사용하여 정적분 찾기
정의에 따라, 정적분은 기본적으로 합계의 한계입니다. 곡선과 x 축 사이의 영역과 두 곡선 사이의 영역과 같은 영역을 찾기 위해 명확한 적분을 사용합니다. 한정적 분은 필요한 양을 합계의 한계로 표현할 수있는 다른 상황에서도 사용할 수 있습니다.
그만큼 int 함수는 적분을 계산하려는 한계를 전달하여 명확한 적분에 사용할 수 있습니다.
계산하려면
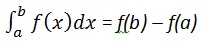
우리는 쓴다,
int(x, a, b)예를 들어,

int(x, 4, 9)MATLAB은 위의 문을 실행하고 다음 결과를 반환합니다.
ans =
65/2다음은 위의 계산에 해당하는 옥타브입니다.
pkg load symbolic
symbols
x = sym("x");
f = x;
c = [1, 0];
integral = polyint(c);
a = polyval(integral, 9) - polyval(integral, 4);
display('Area: '), disp(double(a));Octave는 코드를 실행하고 다음 결과를 반환합니다.
Area:
32.500다음과 같이 Octave에서 제공하는 quad () 함수를 사용하여 대체 솔루션을 제공 할 수 있습니다.
pkg load symbolic
symbols
f = inline("x");
[a, ierror, nfneval] = quad(f, 4, 9);
display('Area: '), disp(double(a));Octave는 코드를 실행하고 다음 결과를 반환합니다.
Area:
32.500예 1
x 축과 곡선 y = x 3 −2x + 5 및 세로 좌표 x = 1 및 x = 2 사이에있는 면적을 계산해 보겠습니다 .
필요한 면적은 다음과 같습니다.
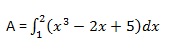
스크립트 파일을 만들고 다음 코드를 입력하십시오-
f = x^3 - 2*x +5;
a = int(f, 1, 2)
display('Area: '), disp(double(a));파일을 실행하면 다음 결과가 표시됩니다.
a =
23/4
Area:
5.7500다음은 위의 계산에 해당하는 옥타브입니다.
pkg load symbolic
symbols
x = sym("x");
f = x^3 - 2*x +5;
c = [1, 0, -2, 5];
integral = polyint(c);
a = polyval(integral, 2) - polyval(integral, 1);
display('Area: '), disp(double(a));Octave는 코드를 실행하고 다음 결과를 반환합니다.
Area:
5.7500다음과 같이 Octave에서 제공하는 quad () 함수를 사용하여 대체 솔루션을 제공 할 수 있습니다.
pkg load symbolic
symbols
x = sym("x");
f = inline("x^3 - 2*x +5");
[a, ierror, nfneval] = quad(f, 1, 2);
display('Area: '), disp(double(a));Octave는 코드를 실행하고 다음 결과를 반환합니다.
Area:
5.7500예 2
곡선 아래 영역을 찾으십시오 . −4 ≤ x ≤ 9에 대해 f (x) = x 2 cos (x)
스크립트 파일을 만들고 다음 코드를 작성하십시오-
f = x^2*cos(x);
ezplot(f, [-4,9])
a = int(f, -4, 9)
disp('Area: '), disp(double(a));파일을 실행하면 MATLAB은 그래프를 플로팅합니다.
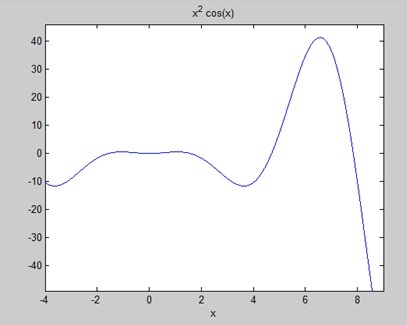
출력은 다음과 같습니다.
a =
8*cos(4) + 18*cos(9) + 14*sin(4) + 79*sin(9)
Area:
0.3326다음은 위의 계산에 해당하는 옥타브입니다.
pkg load symbolic
symbols
x = sym("x");
f = inline("x^2*cos(x)");
ezplot(f, [-4,9])
print -deps graph.eps
[a, ierror, nfneval] = quad(f, -4, 9);
display('Area: '), disp(double(a));