R-선형 회귀

회귀 분석은 두 변수 간의 관계 모델을 설정하기 위해 매우 널리 사용되는 통계 도구입니다. 이러한 변수 중 하나를 예측 변수라고하며 실험을 통해 값을 수집합니다. 다른 변수는 예측 변수에서 값이 파생되는 반응 변수라고합니다.

선형 회귀에서이 두 변수는 방정식을 통해 관련되며 두 변수의 지수 (승수)는 1입니다. 수학적으로 선형 관계는 그래프로 표시 될 때 직선을 나타냅니다. 변수의 지수가 1이 아닌 비선형 관계는 곡선을 만듭니다.

선형 회귀에 대한 일반적인 수학 방정식은 다음과 같습니다.

y = ax + b

다음은 사용 된 매개 변수에 대한 설명입니다.

y 반응 변수입니다.
x 예측 변수입니다.
a 과 b 계수라고하는 상수입니다.

회귀를 설정하는 단계

회귀의 간단한 예는 키를 알고있을 때 사람의 체중을 예측하는 것입니다. 이렇게하려면 사람의 키와 몸무게 사이의 관계가 필요합니다.

관계를 만드는 단계는-

관찰 된 키와 해당 무게 값의 샘플을 수집하는 실험을 수행합니다.
다음을 사용하여 관계 모델을 만듭니다. lm() R의 기능.
생성 된 모델에서 계수를 찾고 다음을 사용하여 수학 방정식을 만듭니다.
예측의 평균 오류를 알기 위해 관계 모델의 요약을 가져옵니다. 또한residuals.
새로운 사람의 체중을 예측하려면 predict() R의 기능.

입력 데이터

다음은 관찰을 나타내는 샘플 데이터입니다.

# Values of height
151, 174, 138, 186, 128, 136, 179, 163, 152, 131

# Values of weight.
63, 81, 56, 91, 47, 57, 76, 72, 62, 48

lm () 함수

이 함수는 예측 변수와 반응 변수 간의 관계 모델을 만듭니다.

통사론

기본 구문 lm() 선형 회귀 함수는-

lm(formula,data)

다음은 사용 된 매개 변수에 대한 설명입니다.

formula x와 y 사이의 관계를 나타내는 기호입니다.
data 수식이 적용될 벡터입니다.

관계 모델 생성 및 계수 얻기

x <- c(151, 174, 138, 186, 128, 136, 179, 163, 152, 131)
y <- c(63, 81, 56, 91, 47, 57, 76, 72, 62, 48)

# Apply the lm() function.
relation <- lm(y~x)

print(relation)

위 코드를 실행하면 다음과 같은 결과가 생성됩니다.

Call:
lm(formula = y ~ x)

Coefficients:
(Intercept)            x  
   -38.4551          0.6746

관계 요약보기

x <- c(151, 174, 138, 186, 128, 136, 179, 163, 152, 131)
y <- c(63, 81, 56, 91, 47, 57, 76, 72, 62, 48)

# Apply the lm() function.
relation <- lm(y~x)

print(summary(relation))

위 코드를 실행하면 다음과 같은 결과가 생성됩니다.

Call:
lm(formula = y ~ x)

Residuals:
    Min      1Q     Median      3Q     Max 
-6.3002    -1.6629  0.0412    1.8944  3.9775 

Coefficients:
             Estimate Std. Error t value Pr(>|t|)    
(Intercept) -38.45509    8.04901  -4.778  0.00139 ** 
x             0.67461    0.05191  12.997 1.16e-06 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

Residual standard error: 3.253 on 8 degrees of freedom
Multiple R-squared:  0.9548,    Adjusted R-squared:  0.9491 
F-statistic: 168.9 on 1 and 8 DF,  p-value: 1.164e-06

predict () 함수

통사론

선형 회귀에서 predict ()의 기본 구문은 다음과 같습니다.

predict(object, newdata)

다음은 사용 된 매개 변수에 대한 설명입니다.

object lm () 함수를 사용하여 이미 생성 된 공식입니다.
newdata 예측 변수의 새 값을 포함하는 벡터입니다.

새로운 사람의 체중 예측

# The predictor vector.
x <- c(151, 174, 138, 186, 128, 136, 179, 163, 152, 131)

# The resposne vector.
y <- c(63, 81, 56, 91, 47, 57, 76, 72, 62, 48)

# Apply the lm() function.
relation <- lm(y~x)

# Find weight of a person with height 170.
a <- data.frame(x = 170)
result <-  predict(relation,a)
print(result)

위 코드를 실행하면 다음과 같은 결과가 생성됩니다.

1 
76.22869

회귀를 그래픽으로 시각화

# Create the predictor and response variable.
x <- c(151, 174, 138, 186, 128, 136, 179, 163, 152, 131)
y <- c(63, 81, 56, 91, 47, 57, 76, 72, 62, 48)
relation <- lm(y~x)

# Give the chart file a name.
png(file = "linearregression.png")

# Plot the chart.
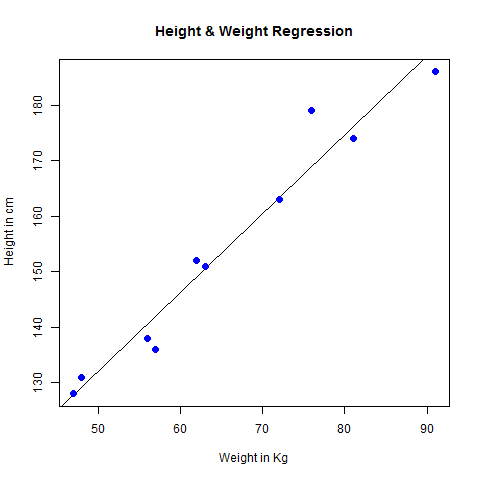
plot(y,x,col = "blue",main = "Height & Weight Regression",
abline(lm(x~y)),cex = 1.3,pch = 16,xlab = "Weight in Kg",ylab = "Height in cm")

# Save the file.
dev.off()

위 코드를 실행하면 다음과 같은 결과가 생성됩니다.