R-비선형 최소 제곱

회귀 분석을 위해 실제 데이터를 모델링 할 때 모델의 방정식이 선형 그래프를 제공하는 선형 방정식 인 경우는 드뭅니다. 대부분의 경우 실제 데이터 모델의 방정식은 지수 3 또는 sin 함수와 같은 더 높은 수준의 수학적 함수를 포함합니다. 이러한 시나리오에서 모델 플롯은 선이 아닌 곡선을 제공합니다. 선형 회귀와 비선형 회귀 모두의 목표는 모델의 매개 변수 값을 조정하여 데이터에 가장 가까운 선이나 곡선을 찾는 것입니다. 이 값을 찾으면 정확한 응답 변수를 추정 할 수 있습니다.

최소 제곱 회귀에서는 회귀 곡선에서 다른 점의 수직 거리 제곱의 합을 최소화하는 회귀 모델을 설정합니다. 우리는 일반적으로 정의 된 모델로 시작하여 계수에 대한 일부 값을 가정합니다. 그런 다음nls() R의 함수를 사용하여 신뢰 구간과 함께 더 정확한 값을 얻습니다.

통사론

R에서 비선형 최소 제곱 테스트를 만드는 기본 구문은 다음과 같습니다.

nls(formula, data, start)

다음은 사용 된 매개 변수에 대한 설명입니다.

• formula 변수와 매개 변수를 포함하는 비선형 모델 공식입니다.

• data 수식의 변수를 평가하는 데 사용되는 데이터 프레임입니다.

• start 시작 추정치의 명명 된 목록 또는 명명 된 숫자 형 벡터입니다.

예

계수의 초기 값을 가정 한 비선형 모델을 고려할 것입니다. 다음으로 이러한 값이 모델에 얼마나 잘 적용되는지 판단 할 수 있도록 이러한 가정 된 값의 신뢰 구간이 무엇인지 확인합니다.

이 목적을 위해 아래 방정식을 고려해 봅시다.

a = b1*x^2+b2

초기 계수를 1과 3으로 가정하고이 값을 nls () 함수에 맞 춥니 다.

xvalues <- c(1.6,2.1,2,2.23,3.71,3.25,3.4,3.86,1.19,2.21)
yvalues <- c(5.19,7.43,6.94,8.11,18.75,14.88,16.06,19.12,3.21,7.58)

# Give the chart file a name.
png(file = "nls.png")


# Plot these values.
plot(xvalues,yvalues)


# Take the assumed values and fit into the model.
model <- nls(yvalues ~ b1*xvalues^2+b2,start = list(b1 = 1,b2 = 3))

# Plot the chart with new data by fitting it to a prediction from 100 data points.
new.data <- data.frame(xvalues = seq(min(xvalues),max(xvalues),len = 100))
lines(new.data$xvalues,predict(model,newdata = new.data))

# Save the file.
dev.off()

# Get the sum of the squared residuals.
print(sum(resid(model)^2))

# Get the confidence intervals on the chosen values of the coefficients.
print(confint(model))

위 코드를 실행하면 다음과 같은 결과가 생성됩니다.

[1] 1.081935
Waiting for profiling to be done...
       2.5%    97.5%
b1 1.137708 1.253135
b2 1.497364 2.496484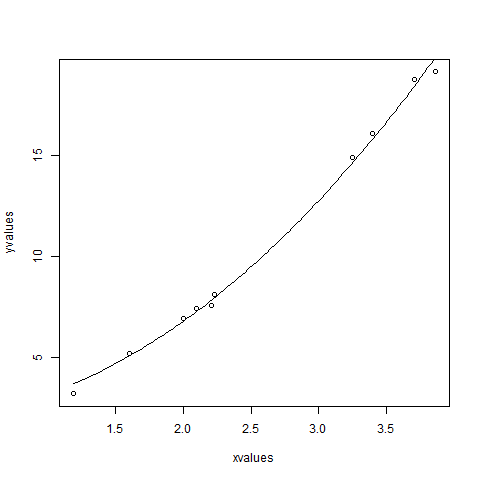

b1의 값은 1에 더 가깝고 b2의 값은 3이 아니라 2에 더 가깝다는 결론을 내릴 수 있습니다.