Deep Learning with Keras - Quick Guide

Deep Learning stało się modnym hasłem ostatnich dni w dziedzinie sztucznej inteligencji (AI). Przez wiele lat używaliśmy uczenia maszynowego (ML) do przekazywania maszynom inteligencji. W ostatnich dniach głębokie uczenie się stało się bardziej popularne ze względu na jego przewagę w przewidywaniach w porównaniu z tradycyjnymi technikami ML.

Głębokie uczenie się zasadniczo oznacza szkolenie sztucznej sieci neuronowej (SSN) z ogromną ilością danych. W uczeniu głębokim sieć uczy się sama, a zatem wymaga ogromnych danych do nauki. Podczas gdy tradycyjne uczenie maszynowe to zasadniczo zestaw algorytmów, które analizują dane i uczą się z nich. Następnie wykorzystali tę wiedzę do podejmowania inteligentnych decyzji.

Teraz, w Keras, jest to interfejs API sieci neuronowych wysokiego poziomu, który działa na TensorFlow - kompleksowej platformie uczenia maszynowego typu open source. Używając Keras, możesz łatwo definiować złożone architektury ANN, aby eksperymentować z dużymi zbiorami danych. Keras obsługuje także GPU, które stają się niezbędne do przetwarzania ogromnych ilości danych i tworzenia modeli uczenia maszynowego.

W tym samouczku nauczysz się wykorzystania Keras w budowaniu głębokich sieci neuronowych. Przyjrzymy się praktycznym przykładom nauczania. Rozpoznawany problem polega na rozpoznawaniu odręcznych cyfr za pomocą sieci neuronowej wyszkolonej przy użyciu głębokiego uczenia.

Aby bardziej podekscytować Cię głębokim uczeniem, poniżej znajduje się zrzut ekranu przedstawiający trendy Google dotyczące głębokiego uczenia się -

Jak widać na diagramie, zainteresowanie głębokim uczeniem się systematycznie rośnie w ciągu ostatnich kilku lat. Istnieje wiele obszarów, takich jak widzenie komputerowe, przetwarzanie języka naturalnego, rozpoznawanie mowy, bioinformatyka, projektowanie leków itd., W których z powodzeniem zastosowano głębokie uczenie się. Ten samouczek pozwoli Ci szybko rozpocząć głębokie uczenie się.

Więc czytaj dalej!

Jak wspomniano we wstępie, głębokie uczenie się to proces uczenia sztucznej sieci neuronowej z ogromną ilością danych. Po przeszkoleniu sieć będzie mogła przekazywać nam prognozy dotyczące niewidocznych danych. Zanim przejdę dalej do wyjaśnienia, czym jest głębokie uczenie się, przejrzyjmy szybko niektóre terminy używane w szkoleniu sieci neuronowej.

Sieci neuronowe

Idea sztucznej sieci neuronowej wywodzi się z sieci neuronowych w naszym mózgu. Typowa sieć neuronowa składa się z trzech warstw - wejściowej, wyjściowej i ukrytej, jak pokazano na poniższym rysunku.

Nazywa się to również shallowsieć neuronowa, ponieważ zawiera tylko jedną ukrytą warstwę. Dodajesz więcej ukrytych warstw w powyższej architekturze, aby stworzyć bardziej złożoną architekturę.

Deep Networks

Poniższy diagram przedstawia głęboką sieć składającą się z czterech ukrytych warstw, warstwy wejściowej i warstwy wyjściowej.

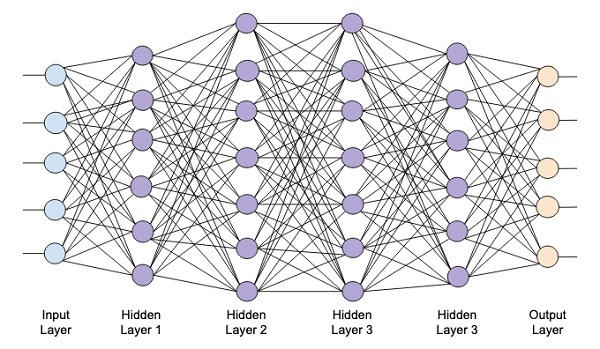
W miarę dodawania liczby warstw ukrytych do sieci jej uczenie staje się bardziej złożone pod względem wymaganych zasobów i czasu potrzebnego do pełnego przeszkolenia sieci.

Szkolenie sieciowe

Po zdefiniowaniu architektury sieci można ją wyszkolić pod kątem wykonywania określonych rodzajów prognoz. Trenowanie sieci to proces znajdowania odpowiednich wag dla każdego łącza w sieci. Podczas szkolenia dane przepływają z warstw wejściowych do wyjściowych przez różne ukryte warstwy. Ponieważ dane zawsze przemieszczają się w jednym kierunku od wejścia do wyjścia, nazywamy tę sieć siecią sprzężenia zwrotnego, a propagację danych nazywamy propagacją naprzód.

Funkcja aktywacji

Na każdej warstwie obliczamy sumę ważoną danych wejściowych i przekazujemy ją do funkcji aktywacji. Funkcja aktywacji wprowadza nieliniowość do sieci. Jest to po prostu jakaś funkcja matematyczna, która dyskretyzuje wynik. Niektóre z najczęściej używanych funkcji aktywacji to sigmoidalne, hiperboliczne, styczne (tanh), ReLU i Softmax.

Propagacja wsteczna

Propagacja wsteczna to algorytm nadzorowanego uczenia się. W Backpropagation błędy są propagowane wstecz z danych wyjściowych do warstwy wejściowej. Mając funkcję błędu, obliczamy gradient funkcji błędu w odniesieniu do wag przypisanych na każdym połączeniu. Obliczanie gradientu przebiega wstecz przez sieć. Gradient ostatniej warstwy odważników jest obliczany jako pierwszy, a gradient pierwszej warstwy odważników jest obliczany jako ostatni.

Na każdej warstwie częściowe obliczenia gradientu są ponownie wykorzystywane do obliczania gradientu dla poprzedniej warstwy. Nazywa się to opadaniem gradientowym.

W tym samouczku opartym na projekcie zdefiniujesz głęboką sieć neuronową ze sprzężeniem zwrotnym i wyszkolisz ją za pomocą technik wstecznej propagacji i gradientu. Na szczęście Keras zapewnia nam wszystkie interfejsy API wysokiego poziomu do definiowania architektury sieci i trenowania jej przy użyciu gradientu. Następnie dowiesz się, jak to zrobić w Keras.

System rozpoznawania odręcznych cyfr

W tym mini projekcie zastosujesz techniki opisane wcześniej. Utworzysz sieć neuronową do głębokiego uczenia się, która zostanie przeszkolona w zakresie rozpoznawania odręcznych cyfr. W każdym projekcie uczenia maszynowego pierwszym wyzwaniem jest zebranie danych. Szczególnie w przypadku sieci uczenia głębokiego potrzebne są ogromne dane. Na szczęście dla problemu, który próbujemy rozwiązać, ktoś już stworzył zbiór danych do treningu. Nazywa się to mnist, który jest dostępny jako część bibliotek Keras. Zbiór danych składa się z kilku obrazów o wymiarach 28 x 28 pikseli z odręcznymi cyframi. Będziesz trenować swój model na głównej części tego zbioru danych, a reszta danych będzie używana do walidacji wytrenowanego modelu.

Opis Projektu

Plik mnistzbiór danych składa się z 70000 obrazów z odręcznymi cyframi. Poniżej przedstawiono kilka przykładowych obrazów w celach informacyjnych

Każdy obraz ma rozmiar 28 x 28 pikseli, co daje w sumie 768 pikseli o różnych poziomach szarości. Większość pikseli ma tendencję do czarnego odcienia, a tylko kilka z nich jest w kolorze białym. Umieścimy rozkład tych pikseli w tablicy lub wektorze. Na przykład rozkład pikseli dla typowego obrazu cyfr 4 i 5 pokazano na poniższym rysunku.

Wyraźnie widać, że rozkład pikseli (zwłaszcza tych zmierzających do białego odcienia) różni się, co pozwala odróżnić cyfry, które reprezentują. Podamy tę dystrybucję 784 pikseli do naszej sieci jako jej dane wejściowe. Dane wyjściowe sieci będą składać się z 10 kategorii reprezentujących cyfrę od 0 do 9.

Nasza sieć będzie składać się z 4 warstw - jednej warstwy wejściowej, jednej wyjściowej i dwóch ukrytych. Każda ukryta warstwa będzie zawierała 512 węzłów. Każda warstwa jest w pełni połączona z następną warstwą. Kiedy trenujemy sieć, będziemy obliczać wagi dla każdego połączenia. Szkolimy sieć, stosując propagację wsteczną i zniżanie w gradiencie, które omówiliśmy wcześniej.

Na tym tle zacznijmy teraz tworzyć projekt.

Konfiguracja projektu

Użyjemy Jupyter przez Anacondanawigator dla naszego projektu. Ponieważ nasz projekt korzysta z TensorFlow i Keras, musisz je zainstalować w konfiguracji Anaconda. Aby zainstalować Tensorflow, uruchom następujące polecenie w oknie konsoli:

>conda install -c anaconda tensorflow

Aby zainstalować Keras, użyj następującego polecenia -

>conda install -c anaconda keras

Jesteś teraz gotowy, aby uruchomić Jupyter.

Uruchamiam Jupyter

Po uruchomieniu nawigatora Anaconda zobaczysz następujący ekran początkowy.

Kliknij ‘Jupyter’żeby to rozpocząć. Na ekranie pojawią się istniejące projekty, jeśli takie istnieją, na dysku.

Rozpoczęcie nowego projektu

Uruchom nowy projekt Python 3 w Anaconda, wybierając następującą opcję menu -

File | New Notebook | Python 3

Zrzut ekranu wyboru menu jest pokazany w celu szybkiego odniesienia -

Nowy pusty projekt pojawi się na ekranie, jak pokazano poniżej -

Zmień nazwę projektu na DeepLearningDigitRecognition klikając i edytując domyślną nazwę “UntitledXX”.

Najpierw importujemy różne biblioteki wymagane przez kod w naszym projekcie.

Obsługa i drukowanie tablic

Jak zwykle używamy numpy do obsługi tablic i matplotlibdo kreślenia. Te biblioteki są importowane do naszego projektu przy użyciu następującego plikuimport sprawozdania

import numpy as np
import matplotlib
import matplotlib.pyplot as plot

Pomijanie ostrzeżeń

Ponieważ zarówno Tensorflow, jak i Keras ciągle poprawiają, jeśli nie zsynchronizujesz ich odpowiednich wersji w projekcie, w czasie wykonywania zobaczysz wiele błędów ostrzegawczych. Ponieważ odwracają twoją uwagę od uczenia się, będziemy tłumić wszystkie ostrzeżenia w tym projekcie. Odbywa się to za pomocą następujących wierszy kodu -

# silent all warnings
import os
os.environ['TF_CPP_MIN_LOG_LEVEL']='3'
import warnings
warnings.filterwarnings('ignore')
from tensorflow.python.util import deprecation
deprecation._PRINT_DEPRECATION_WARNINGS = False

Keras

Korzystamy z bibliotek Keras do importu zbioru danych. Będziemy używaćmnistzbiór danych dla odręcznych cyfr. Importujemy wymagany pakiet, korzystając z poniższej instrukcji

from keras.datasets import mnist

Będziemy definiować naszą sieć neuronową uczenia głębokiego za pomocą pakietów Keras. ImportujemySequential, Dense, Dropout i Activationpakiety do definiowania architektury sieci. Używamyload_modelpakiet do zapisywania i pobierania naszego modelu. Używamy równieżnp_utilsza kilka narzędzi, których potrzebujemy w naszym projekcie. Te importy są wykonywane za pomocą następujących instrukcji programu -

from keras.models import Sequential, load_model
from keras.layers.core import Dense, Dropout, Activation
from keras.utils import np_utils

Po uruchomieniu tego kodu na konsoli zostanie wyświetlony komunikat z informacją, że Keras używa TensorFlow na zapleczu. Zrzut ekranu na tym etapie jest pokazany tutaj -

Teraz, gdy mamy wszystkie importy wymagane przez nasz projekt, przejdziemy do zdefiniowania architektury naszej sieci Deep Learning.

Nasz model sieci neuronowej będzie składał się z liniowego stosu warstw. Aby zdefiniować taki model, nazywamySequential funkcja -

model = Sequential()

Warstwa wejściowa

Warstwę wejściową, która jest pierwszą warstwą w naszej sieci, definiujemy za pomocą następującej instrukcji programu -

model.add(Dense(512, input_shape=(784,)))

Tworzy to warstwę z 512 węzłami (neuronami) z 784 węzłami wejściowymi. Przedstawiono to na poniższym rysunku -

Zauważ, że wszystkie węzły wejściowe są w pełni połączone z warstwą 1, to znaczy każdy węzeł wejściowy jest połączony ze wszystkimi 512 węzłami warstwy 1.

Następnie musimy dodać funkcję aktywacji dla wyjścia warstwy 1. Użyjemy ReLU jako naszej aktywacji. Funkcję aktywacji dodaje się za pomocą następującej instrukcji programu -

model.add(Activation('relu'))

Następnie dodajemy porzucenie 20%, korzystając z poniższego oświadczenia. Dropout to technika używana do zapobiegania nadmiernemu dopasowaniu modelu.

model.add(Dropout(0.2))

W tym momencie nasza warstwa wejściowa jest w pełni zdefiniowana. Następnie dodamy ukrytą warstwę.

Ukryta warstwa

Nasza ukryta warstwa będzie składać się z 512 węzłów. Dane wejściowe do warstwy ukrytej pochodzą z naszej wcześniej zdefiniowanej warstwy wejściowej. Wszystkie węzły są w pełni połączone, jak we wcześniejszym przypadku. Wyjście warstwy ukrytej przejdzie do następnej warstwy w sieci, która będzie naszą ostatnią i wyjściową warstwą. Użyjemy tej samej aktywacji ReLU, co w przypadku poprzedniej warstwy i spadku o 20%. Kod dodawania tej warstwy znajduje się tutaj -

model.add(Dense(512))
model.add(Activation('relu'))
model.add(Dropout(0.2))

Sieć na tym etapie można wizualizować w następujący sposób -

Następnie dodamy ostatnią warstwę do naszej sieci, czyli warstwę wyjściową. Pamiętaj, że możesz dodać dowolną liczbę ukrytych warstw, używając kodu podobnego do tego, którego użyłeś tutaj. Dodanie większej liczby warstw uczyniłoby sieć skomplikowaną pod względem szkolenia; jednak dające zdecydowaną przewagę lepszych wyników w wielu przypadkach, choć nie we wszystkich.

Warstwa wyjściowa

Warstwa wyjściowa składa się z zaledwie 10 węzłów, ponieważ chcemy sklasyfikować dane obrazy za pomocą 10 różnych cyfr. Dodajemy tę warstwę, używając następującego oświadczenia -

model.add(Dense(10))

Ponieważ chcemy podzielić wyjście na 10 różnych jednostek, używamy aktywacji softmax. W przypadku ReLU wyjście jest binarne. Dodajemy aktywację za pomocą następującego oświadczenia -

model.add(Activation('softmax'))

W tym momencie naszą sieć można wizualizować, jak pokazano na poniższym schemacie -

W tym momencie nasz model sieci jest w pełni zdefiniowany w oprogramowaniu. Uruchom komórkę kodu i jeśli nie ma błędów, na ekranie pojawi się komunikat potwierdzający, jak pokazano na zrzucie ekranu poniżej -

Następnie musimy skompilować model.

Kompilacja jest wykonywana przy użyciu jednego wywołania metody o nazwie compile.

model.compile(loss='categorical_crossentropy', metrics=['accuracy'], optimizer='adam')

Plik compilemetoda wymaga kilku parametrów. Parametr strat jest określony jako typ'categorical_crossentropy'. Parametr metryki jest ustawiony na'accuracy' i wreszcie używamy adamoptymalizator do szkolenia sieci. Wynik na tym etapie pokazano poniżej -

Teraz jesteśmy gotowi do wprowadzenia danych do naszej sieci.

Ładowanie danych

Jak wspomniano wcześniej, użyjemy rozszerzenia mnistzbiór danych dostarczony przez Keras. Kiedy ładujemy dane do naszego systemu, podzielimy je na dane treningowe i testowe. Dane są ładowane przez wywołanieload_data metoda w następujący sposób -

(X_train, y_train), (X_test, y_test) = mnist.load_data()

Wynik na tym etapie wygląda następująco -

Teraz nauczymy się struktury załadowanego zbioru danych.

Dostarczone nam dane to obrazy graficzne o wymiarach 28 x 28 pikseli, z których każdy zawiera jedną cyfrę z przedziału od 0 do 9. Pierwsze dziesięć obrazów wyświetlimy na konsoli. Kod umożliwiający to podano poniżej -

# printing first 10 images
for i in range(10):

plot.subplot(3,5,i+1)
plot.tight_layout()
plot.imshow(X_train[i], cmap='gray', interpolation='none')
plot.title("Digit: {}".format(y_train[i]))
plot.xticks([])
plot.yticks([])

W iteracyjnej pętli 10 zliczeń tworzymy podplot dla każdej iteracji i pokazujemy obraz z X_trainwektor w nim. Tytułem każdego obrazu z odpowiedniegoy_trainwektor. Zwróć uwagę, żey_train vector zawiera rzeczywiste wartości dla odpowiedniego obrazu w formacie X_trainwektor. Oznaczenia osi X i Y usuwamy, wywołując obie metodyxticks i yticksz pustym argumentem. Po uruchomieniu kodu zobaczysz następujące dane wyjściowe -

Następnie przygotujemy dane do wprowadzenia ich do naszej sieci.

Zanim prześlemy dane do naszej sieci, należy je przekonwertować do formatu wymaganego przez sieć. Nazywa się to przygotowywaniem danych do sieci. Zwykle polega na przekształceniu wielowymiarowych danych wejściowych na jednowymiarowy wektor i normalizacji punktów danych.

Zmiana kształtu wektora wejściowego

Obrazy w naszym zbiorze danych składają się z 28 x 28 pikseli. To musi zostać zamienione na jednowymiarowy wektor o rozmiarze 28 * 28 = 784, aby wprowadzić go do naszej sieci. Robimy to, dzwoniąc doreshape metoda na wektorze.

X_train = X_train.reshape(60000, 784)
X_test = X_test.reshape(10000, 784)

Teraz nasz wektor uczący będzie składał się z 60000 punktów danych, z których każdy będzie składał się z pojedynczego wektora wymiaru o rozmiarze 784. Podobnie, nasz wektor testowy będzie składał się z 10000 punktów danych jednego wektora wymiarowego o rozmiarze 784.

Normalizowanie danych

Dane, które zawiera wektor wejściowy, mają obecnie dyskretną wartość między 0 a 255 - poziomy skali szarości. Normalizacja tych wartości pikseli między 0 a 1 pomaga w przyspieszeniu treningu. Ponieważ zamierzamy używać stochastycznego spadku gradientu, normalizacja danych pomoże również zmniejszyć ryzyko utknięcia w lokalnych optymach.

Aby znormalizować dane, reprezentujemy je jako typ zmiennoprzecinkowy i dzielimy przez 255, jak pokazano w poniższym fragmencie kodu -

X_train = X_train.astype('float32')
X_test = X_test.astype('float32')
X_train /= 255
X_test /= 255

Przyjrzyjmy się teraz, jak wyglądają znormalizowane dane.

Badanie znormalizowanych danych

Aby wyświetlić znormalizowane dane, wywołamy funkcję histogramu, jak pokazano tutaj -

plot.hist(X_train[0])
plot.title("Digit: {}".format(y_train[0]))

Tutaj wykreślamy histogram pierwszego elementu X_trainwektor. Drukujemy również cyfrę reprezentowaną przez ten punkt danych. Tutaj pokazano wynik uruchomienia powyższego kodu -

Zauważysz gęstą gęstość punktów o wartości bliskiej zeru. Są to czarne punkty na obrazie, które oczywiście stanowią główną część obrazu. Reszta punktów skali szarości, które są zbliżone do koloru białego, reprezentują cyfrę. Możesz sprawdzić rozkład pikseli dla innej cyfry. Poniższy kod drukuje histogram cyfry o indeksie 2 w zestawie danych uczących.

plot.hist(X_train[2])
plot.title("Digit: {}".format(y_train[2])

Wynik uruchomienia powyższego kodu pokazano poniżej -

Porównując powyższe dwie figury, zauważysz, że rozkład białych pikseli na dwóch obrazach różni się, co wskazuje na reprezentację innej cyfry - „5” i „4” na dwóch powyższych zdjęciach.

Następnie zbadamy dystrybucję danych w naszym pełnym zestawie danych szkoleniowych.

Badanie dystrybucji danych

Zanim wytrenujemy nasz model uczenia maszynowego w naszym zbiorze danych, powinniśmy znać rozkład unikatowych cyfr w naszym zbiorze danych. Nasze obrazy przedstawiają 10 różnych cyfr w zakresie od 0 do 9. Chcielibyśmy poznać liczbę cyfr 0, 1 itd. W naszym zbiorze danych. Możemy uzyskać te informacje za pomocąunique metoda Numpy.

Użyj następującego polecenia, aby wydrukować liczbę unikatowych wartości i liczbę wystąpień każdej z nich

print(np.unique(y_train, return_counts=True))

Po uruchomieniu powyższego polecenia zobaczysz następujące dane wyjściowe -

(array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9], dtype=uint8), array([5923, 6742, 5958, 6131, 5842, 5421, 5918, 6265, 5851, 5949]))

Pokazuje, że istnieje 10 różnych wartości - od 0 do 9. Istnieje 5923 wystąpień cyfry 0, 6742 wystąpień cyfry 1 i tak dalej. Tutaj pokazano zrzut ekranu wyjścia -

Na ostatnim etapie przygotowania danych musimy zakodować nasze dane.

Kodowanie danych

W naszym zbiorze danych mamy dziesięć kategorii. W ten sposób zakodujemy nasze dane wyjściowe w tych dziesięciu kategoriach przy użyciu kodowania na gorąco. Do kodowania używamy metody to_categorial narzędzi Numpy. Po zakodowaniu danych wyjściowych każdy punkt danych zostanie przekształcony w jednowymiarowy wektor o rozmiarze 10. Na przykład cyfra 5 będzie teraz reprezentowana jako [0,0,0,0,0,1,0,0,0 , 0].

Zakoduj dane za pomocą następującego fragmentu kodu -

n_classes = 10
Y_train = np_utils.to_categorical(y_train, n_classes)

Możesz sprawdzić wynik kodowania, drukując pierwsze 5 elementów skategoryzowanego wektora Y_train.

Użyj poniższego kodu, aby wydrukować pierwsze 5 wektorów -

for i in range(5):
   print (Y_train[i])

Zobaczysz następujący wynik -

[0. 0. 0. 0. 0. 1. 0. 0. 0. 0.]
[1. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 1. 0. 0. 0. 0. 0.]
[0. 1. 0. 0. 0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0. 0. 0. 0. 1.]

Pierwszy element reprezentuje cyfrę 5, drugi oznacza cyfrę 0 i tak dalej.

Na koniec będziesz musiał również sklasyfikować dane testowe, co odbywa się za pomocą następującego stwierdzenia -

Y_test = np_utils.to_categorical(y_test, n_classes)

Na tym etapie Twoje dane są w pełni przygotowane do wprowadzenia do sieci.

Następna jest najważniejsza część, czyli szkolenie naszego modelu sieci.

Uczenie modelu odbywa się za pomocą jednego wywołania metody o nazwie fit, które wymaga kilku parametrów, jak widać w poniższym kodzie -

history = model.fit(X_train, Y_train,
   batch_size=128, epochs=20,
   verbose=2,
   validation_data=(X_test, Y_test)))

Pierwsze dwa parametry metody dopasowania określają funkcje i dane wyjściowe zestawu danych szkoleniowych.

Plik epochsjest ustawiony na 20; zakładamy, że szkolenie będzie zbieżne w maksymalnie 20 epokach - iteracjach. Wytrenowany model jest sprawdzany na podstawie danych testowych, jak określono w ostatnim parametrze.

Tutaj pokazano częściowe wyniki uruchomienia powyższego polecenia -

Train on 60000 samples, validate on 10000 samples
Epoch 1/20
- 9s - loss: 0.2488 - acc: 0.9252 - val_loss: 0.1059 - val_acc: 0.9665
Epoch 2/20
- 9s - loss: 0.1004 - acc: 0.9688 - val_loss: 0.0850 - val_acc: 0.9715
Epoch 3/20
- 9s - loss: 0.0723 - acc: 0.9773 - val_loss: 0.0717 - val_acc: 0.9765
Epoch 4/20
- 9s - loss: 0.0532 - acc: 0.9826 - val_loss: 0.0665 - val_acc: 0.9795
Epoch 5/20
- 9s - loss: 0.0457 - acc: 0.9856 - val_loss: 0.0695 - val_acc: 0.9792

Zrzut ekranu przedstawiający dane wyjściowe znajduje się poniżej w celu szybkiego odniesienia -

Teraz, gdy model jest szkolony na podstawie naszych danych szkoleniowych, ocenimy jego wydajność.

Aby ocenić wydajność modelu, dzwonimy evaluate metoda w następujący sposób -

loss_and_metrics = model.evaluate(X_test, Y_test, verbose=2)

Aby ocenić wydajność modelu, dzwonimy evaluate metoda w następujący sposób -

loss_and_metrics = model.evaluate(X_test, Y_test, verbose=2)

Wydrukujemy utratę i dokładność, korzystając z następujących dwóch stwierdzeń -

print("Test Loss", loss_and_metrics[0])
print("Test Accuracy", loss_and_metrics[1])

Po uruchomieniu powyższych instrukcji zobaczysz następujące dane wyjściowe -

Test Loss 0.08041584826191042
Test Accuracy 0.9837

To pokazuje dokładność testu 98%, co powinno być dla nas akceptowalne. Co dla nas oznacza, że w 2% przypadków odręczne cyfry nie zostałyby poprawnie sklasyfikowane. Będziemy również wykreślać dokładność i metryki strat, aby zobaczyć, jak model działa na danych testowych.

Wykreślanie metryk dokładności

Używamy nagranych historypodczas naszego szkolenia, aby uzyskać wykres metryk dokładności. Poniższy kod wykreśla dokładność dla każdej epoki. Zbieramy dokładność danych treningowych („acc”) i dokładność danych walidacyjnych („val_acc”) do wykreślenia.

plot.subplot(2,1,1)
plot.plot(history.history['acc'])
plot.plot(history.history['val_acc'])
plot.title('model accuracy')
plot.ylabel('accuracy')
plot.xlabel('epoch')
plot.legend(['train', 'test'], loc='lower right')

Wykres wyjściowy pokazano poniżej -

Jak widać na diagramie, dokładność szybko rośnie w pierwszych dwóch epokach, co wskazuje, że sieć szybko się uczy. Następnie krzywa spłaszcza się, co wskazuje, że nie potrzeba zbyt wielu epok, aby dalej trenować model. Ogólnie rzecz biorąc, jeśli dokładność danych uczących („acc”) stale się poprawia, podczas gdy dokładność danych walidacyjnych („val_acc”) pogarsza się, występuje nadmierne dopasowanie. Wskazuje, że model zaczyna zapamiętywać dane.

Będziemy również wykreślać wskaźniki strat, aby sprawdzić wydajność naszego modelu.

Wykreślanie wskaźników strat

Ponownie wykreślamy stratę zarówno na danych uczących („strata”), jak i testowych („strat_wartości”). Odbywa się to za pomocą następującego kodu -

plot.subplot(2,1,2)
plot.plot(history.history['loss'])
plot.plot(history.history['val_loss'])
plot.title('model loss')
plot.ylabel('loss')
plot.xlabel('epoch')
plot.legend(['train', 'test'], loc='upper right')

Wynik tego kodu pokazano poniżej -

Jak widać na wykresie, strata na zbiorze uczącym gwałtownie maleje w pierwszych dwóch epokach. W przypadku zestawu testowego strata nie zmniejsza się w tym samym tempie co zbiór uczący, ale pozostaje prawie płaska przez wiele epok. Oznacza to, że nasz model dobrze uogólnia niewidoczne dane.

Teraz użyjemy naszego wytrenowanego modelu do przewidywania cyfr w naszych danych testowych.

Przewidywanie cyfr w niewidocznych danych jest bardzo łatwe. Wystarczy zadzwonić pod numerpredict_classes metoda model przekazując go do wektora składającego się z nieznanych punktów danych.

predictions = model.predict_classes(X_test)

Wywołanie metody zwraca przewidywania w wektorze, które można sprawdzić pod kątem zer i jedynek względem rzeczywistych wartości. Odbywa się to za pomocą następujących dwóch instrukcji -

correct_predictions = np.nonzero(predictions == y_test)[0]
incorrect_predictions = np.nonzero(predictions != y_test)[0]

Na koniec wydrukujemy liczbę poprawnych i niepoprawnych przewidywań, korzystając z następujących dwóch instrukcji programu -

print(len(correct_predictions)," classified correctly")
print(len(incorrect_predictions)," classified incorrectly")

Po uruchomieniu kodu otrzymasz następujące dane wyjściowe -

9837 classified correctly
163 classified incorrectly

Teraz, po zadowalającym przeszkoleniu modelu, zachowamy go do wykorzystania w przyszłości.

Zapiszemy wytrenowany model na naszym dysku lokalnym w folderze models w naszym bieżącym katalogu roboczym. Aby zapisać model, uruchom następujący kod -

directory = "./models/"
name = 'handwrittendigitrecognition.h5'
path = os.path.join(save_dir, name)
model.save(path)
print('Saved trained model at %s ' % path)

Wynik po uruchomieniu kodu pokazano poniżej -

Teraz, po zapisaniu wytrenowanego modelu, możesz użyć go później do przetwarzania nieznanych danych.

Aby przewidzieć niewidoczne dane, musisz najpierw załadować wytrenowany model do pamięci. Odbywa się to za pomocą następującego polecenia -

model = load_model ('./models/handwrittendigitrecognition.h5')

Zwróć uwagę, że po prostu ładujemy plik .h5 do pamięci. To ustawia całą sieć neuronową w pamięci wraz z wagami przypisanymi do każdej warstwy.

Teraz, aby przewidzieć niewidoczne dane, załaduj dane, niech to będzie jeden lub więcej elementów, do pamięci. Przetwórz wstępnie dane, aby spełnić wymagania wejściowe naszego modelu, tak jak w przypadku powyższych danych treningowych i testowych. Po wstępnym przetworzeniu prześlij go do swojej sieci. Model wyświetli swoje przewidywania.

Keras zapewnia interfejs API wysokiego poziomu do tworzenia głębokich sieci neuronowych. W tym samouczku nauczyłeś się tworzyć głęboką sieć neuronową, która została wyszkolona do znajdowania cyfr w odręcznym tekście. W tym celu stworzono sieć wielowarstwową. Keras umożliwia zdefiniowanie wybranej funkcji aktywacji na każdej warstwie. Wykorzystując opadanie gradientowe, sieć została przeszkolona na danych uczących. Dokładność wytrenowanej sieci w przewidywaniu niewidocznych danych została przetestowana na danych testowych. Nauczyłeś się wykreślać metryki dokładności i błędów. Po pełnym przeszkoleniu sieci model sieci został zapisany do wykorzystania w przyszłości.