Szeregi Fouriera i transformacja

W ostatnim samouczku dotyczącym analizy w dziedzinie częstotliwości omówiliśmy, że szereg Fouriera i transformata Fouriera są używane do konwersji sygnału do dziedziny częstotliwości.

Fouriera

Fourier był matematykiem w 1822 roku. Podał szereg Fouriera i transformatę Fouriera, aby przekształcić sygnał w dziedzinę częstotliwości.

Szereg Fouriera

Szereg Fouriera stwierdza po prostu, że sygnały okresowe można przedstawić jako sumę sinusów i cosinusów po pomnożeniu ich przez określoną wagę, a ponadto stwierdza się, że sygnały okresowe można podzielić na dalsze sygnały o następujących właściwościach.

Sygnały to sinus i cosinus
Sygnały są wzajemnymi harmonicznymi

Można to obrazowo postrzegać jako

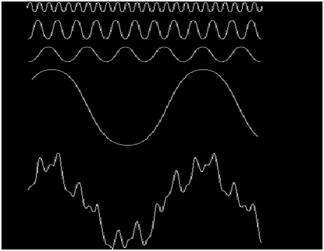
W powyższym sygnale ostatni sygnał jest w rzeczywistości sumą wszystkich powyższych sygnałów. Taka była idea Fouriera.

Jak to jest obliczane

Ponieważ, jak widzieliśmy w dziedzinie częstotliwości, aby przetworzyć obraz w dziedzinie częstotliwości, musimy najpierw przekształcić go za pomocą domeny częstotliwości i musimy wziąć odwrotność wyniku, aby przekształcić go z powrotem w domenę przestrzenną. Dlatego zarówno szereg Fouriera, jak i transformata Fouriera mają dwa wzory. Jeden do konwersji, a drugi do konwersji z powrotem do domeny przestrzennej.

Szereg Fouriera

Szereg Fouriera można oznaczyć tym wzorem.

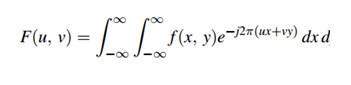
Odwrotność można obliczyć za pomocą tego wzoru.

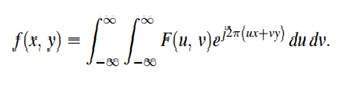
Przekształcenie Fouriera

Przekształcenie Fouriera stwierdza po prostu, że sygnały nieokresowe, których pole powierzchni pod krzywą jest skończone, można również przedstawić w całkach sinusów i cosinusów po pomnożeniu ich przez określoną wagę.

Transformacja Fouriera ma wiele szerokich zastosowań, które obejmują kompresję obrazu (np. Kompresję JPEG), filtrowanie i analizę obrazu.

Różnica między szeregiem Fouriera a transformacją

Chociaż zarówno szereg Fouriera, jak i transformata Fouriera są podane przez Fouriera, ale różnica między nimi polega na tym, że szereg Fouriera jest stosowany do sygnałów okresowych, a transformata Fouriera jest stosowana do sygnałów nieokresowych

Który jest stosowany na obrazach

Teraz pozostaje pytanie, który z nich zostanie zastosowany na obrazach, szereg Fouriera czy transformata Fouriera. Cóż, odpowiedź na to pytanie polega na tym, że jakie są obrazy. Obrazy są nieokresowe. A ponieważ obrazy nie są okresowe, więc transformata Fouriera jest używana do konwersji ich do domeny częstotliwości.

Dyskretna transformata Fouriera

Ponieważ mamy do czynienia z obrazami, a właściwie obrazami cyfrowymi, więc dla obrazów cyfrowych będziemy pracować nad dyskretną transformatą Fouriera

Rozważ powyższy wyraz Fouriera sinusoidy. Obejmuje trzy rzeczy.

Częstotliwość przestrzenna
Magnitude
Phase

Częstotliwość przestrzenna jest bezpośrednio związana z jasnością obrazu. Wielkość sinusoidy jest bezpośrednio związana z kontrastem. Kontrast to różnica między maksymalną i minimalną intensywnością pikseli. Faza zawiera informacje o kolorze.

Wzór na dwuwymiarową dyskretną transformatę Fouriera podano poniżej.

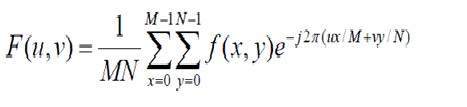
Dyskretna transformata Fouriera jest w rzeczywistości próbkowaną transformatą Fouriera, więc zawiera pewne próbki, które oznaczają obraz. W powyższym wzorze f (x, y) oznacza obraz, a F (u, v) oznacza dyskretną transformatę Fouriera. Wzór na dwuwymiarową odwrotną dyskretną transformację Fouriera podano poniżej.

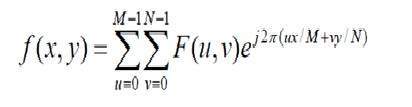
Odwrotna dyskretna transformata Fouriera przekształca transformatę Fouriera z powrotem w obraz

Rozważ ten sygnał

Teraz zobaczymy obraz, na którym obliczymy widmo wielkości FFT, a następnie przesunięte widmo wielkości FFT, a następnie weźmiemy Log z tego przesuniętego widma.