Transformacje obrazu
Zanim omówimy, czym jest transformacja obrazu, omówimy, czym jest transformacja.
Transformacja
Transformacja jest funkcją. Funkcja, która mapuje jeden zestaw na inny zestaw po wykonaniu niektórych operacji.
System cyfrowego przetwarzania obrazu
Widzieliśmy już we wprowadzających samouczkach, że w cyfrowym przetwarzaniu obrazu opracujemy system, którego wejście będzie obrazem, a wyjście również obrazem. System przeprowadziłby pewne przetwarzanie na obrazie wejściowym i dałby wynik jako przetworzony obraz. Jest to pokazane poniżej.
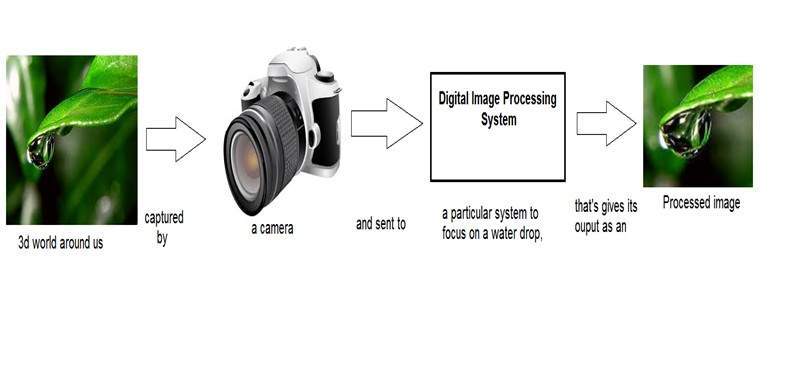
Funkcję zastosowaną w tym systemie cyfrowym, która przetwarza obraz i przekształca go w wyjście, można nazwać funkcją transformacji.
Jak pokazuje transformację lub relację, to jak obraz1 jest konwertowany na obraz2.
Transformacja obrazu.
Rozważ to równanie
G (x, y) = T {f (x, y)}
W tym równaniu
F (x, y) = obraz wejściowy, na którym ma zostać zastosowana funkcja transformacji.
G (x, y) = obraz wyjściowy lub obraz przetworzony.
T jest funkcją transformacji.
Ten związek między obrazem wejściowym a przetworzonym obrazem wyjściowym można również przedstawić jako.
s = T (r)
gdzie r jest w rzeczywistości wartością piksela lub intensywnością poziomu szarości f (x, y) w dowolnym punkcie. A s to wartość piksela lub intensywność poziomu szarości g (x, y) w dowolnym punkcie.
Podstawowa transformacja poziomu szarości została omówiona w naszym tutorialu na temat podstawowych transformacji poziomu szarości.
Teraz omówimy niektóre z bardzo podstawowych funkcji transformacji.
Przykłady
Rozważ tę funkcję transformacji.
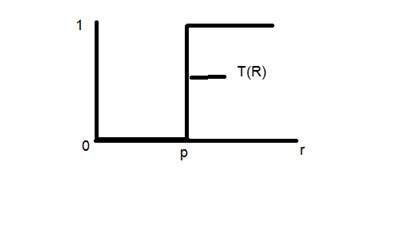
Przyjmijmy, że punkt r wynosi 256, a punkt p 127. Rozważmy ten obraz jako obraz o jednym bpp. Oznacza to, że mamy tylko dwa poziomy intensywności, które są 0 i 1. W tym przypadku transformację pokazaną na wykresie można wyjaśnić jako.
Wszystkie wartości intensywności pikseli poniżej 127 (punkt p) wynoszą 0, co oznacza czerń. Wszystkie wartości intensywności pikseli, które są większe niż 127, wynoszą 1, co oznacza biel. Ale dokładnie w punkcie 127 następuje nagła zmiana transmisji, więc nie możemy powiedzieć, że w tym dokładnym punkcie wartość wyniesie 0 lub 1.
Matematycznie tę funkcję transformacji można oznaczyć jako:
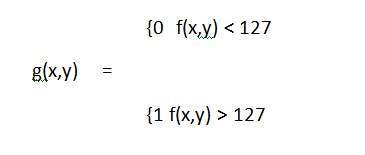
Rozważ inną taką transformację
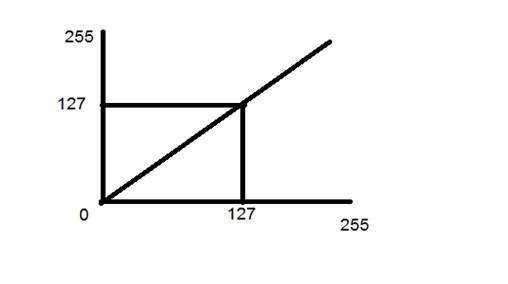
Teraz, jeśli spojrzysz na ten konkretny wykres, zobaczysz prostą linię przejścia między obrazem wejściowym a obrazem wyjściowym.
Pokazuje, że dla każdego piksela lub wartości natężenia obrazu wejściowego istnieje taka sama wartość natężenia obrazu wyjściowego. Oznacza to, że obraz wyjściowy jest dokładną repliką obrazu wejściowego.
Można go matematycznie przedstawić jako:
g (x, y) = f (x, y)
obraz wejściowy i wyjściowy byłby w tym przypadku pokazany poniżej.
