Transformacja poziomu szarości

Omówiliśmy niektóre z podstawowych transformacji w naszym samouczku Transformacja podstawowa. W tym samouczku przyjrzymy się niektórym z podstawowych przekształceń poziomu szarości.

Wzmocnienie obrazu

Ulepszanie obrazu zapewnia lepszy kontrast i bardziej szczegółowy obraz w porównaniu z obrazem bez ulepszenia. Ulepszanie obrazu ma wiele zastosowań. Służy do ulepszania obrazów medycznych, obrazów zarejestrowanych za pomocą teledetekcji, obrazów satelitarnych itp

Funkcja transformacji została podana poniżej

s = T (r)

gdzie r to piksele obrazu wejściowego, a s to piksele obrazu wyjściowego. T jest funkcją transformacji, która odwzorowuje każdą wartość r na każdą wartość s. Wzmocnienie obrazu można przeprowadzić poprzez transformacje poziomu szarości, które omówiono poniżej.

Transformacja poziomu szarości

Istnieją trzy podstawowe transformacje poziomu szarości.

Linear
Logarithmic
Władza - prawo

Ogólny wykres tych przejść pokazano poniżej.

Transformacja liniowa

Najpierw przyjrzymy się transformacji liniowej. Transformacja liniowa obejmuje prostą tożsamość i transformację negatywną. Transformacja tożsamości została omówiona w naszym samouczku dotyczącym transformacji obrazu, ale krótki opis tej transformacji został podany tutaj.

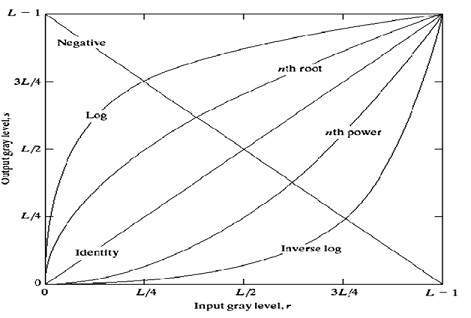
Przejście tożsamości jest pokazane linią prostą. W tym przejściu każda wartość obrazu wejściowego jest bezpośrednio odwzorowywana na inną wartość obrazu wyjściowego. Daje to ten sam obraz wejściowy i obraz wyjściowy. Dlatego nazywa się to transformacją tożsamości. Zostało to pokazane poniżej:

Negatywna transformacja

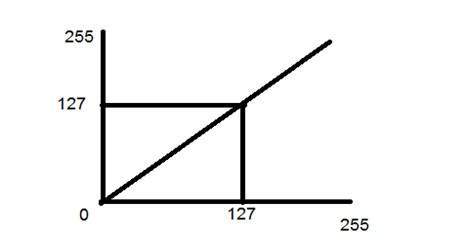
Druga transformacja liniowa to transformacja ujemna, która jest odwrotnością transformacji tożsamości. W transformacji ujemnej każda wartość obrazu wejściowego jest odejmowana od L-1 i odwzorowywana na obraz wyjściowy.

Wynik jest podobny do tego.

Obraz wejściowy

Obraz wyjściowy

W tym przypadku następująca zmiana została wykonana.

s = (L - 1) - r

ponieważ obraz wejściowy Einsteina jest obrazem 8 bpp, więc liczba poziomów na tym obrazie wynosi 256. Wstawiając 256 do równania, otrzymujemy to

s = 255 - r

Tak więc każda wartość jest odejmowana przez 255, a obraz wynikowy pokazano powyżej. Więc co się dzieje, jaśniejsze piksele stają się ciemne, a ciemniejszy obraz staje się jasny. Efektem jest negatywny obraz.

Pokazuje to poniższy wykres.

Transformacje logarytmiczne

Transformacja logarytmiczna zawiera ponadto dwa rodzaje transformacji. Transformacja dziennika i odwrotna transformacja dziennika.

Transformacja dziennika

Transformacje dziennika można zdefiniować za pomocą tego wzoru

s = c log (r + 1).

Gdzie s i r są wartościami pikseli wyjścia, a obraz wejściowy, ic jest stałą. Wartość 1 jest dodawana do każdej wartości piksela obrazu wejściowego, ponieważ jeśli w obrazie występuje intensywność piksela równa 0, wówczas log (0) jest równy nieskończoności. Więc dodaje się 1, aby minimalna wartość wynosiła co najmniej 1.

Podczas transformacji dziennika ciemne piksele obrazu są rozszerzane w porównaniu z większymi wartościami pikseli. Wyższe wartości pikseli są kompresowane w transformacji dziennika. Skutkuje to następującą poprawą obrazu.

Wartość c w transformacji dziennika dostosowuje rodzaj ulepszenia, którego szukasz.

Obraz wejściowy

Loguj obraz tranformy

Odwrotna transformacja logarytmiczna jest odwrotna do transformacji logarytmicznej.

Przekształcenia władzy - prawa

Istnieją dalsze dwie transformacje transformacji prawa potęgowego, które obejmują n-tą potęgę i n-tą transformację pierwiastka. Transformacje te można wyrazić wyrażeniem:

s = cr ^ γ

Ten symbol γ nazywa się gamma, dzięki czemu ta transformacja jest również znana jako transformacja gamma.

Zmiana wartości γ zmienia wzmocnienie obrazu. Różne urządzenia wyświetlające / monitory mają własną korekcję gamma, dlatego wyświetlają swój obraz z różnym natężeniem.

Ten typ transformacji służy do ulepszania obrazów dla różnych typów urządzeń wyświetlających. Gamma różnych urządzeń wyświetlających jest inna. Na przykład Gamma CRT mieści się w zakresie od 1,8 do 2,5, co oznacza, że obraz wyświetlany na CRT jest ciemny.