Obwody elektroniczne - prostowniki

Zawsze, gdy zachodzi potrzeba konwersji prądu zmiennego na prąd stały, na ratunek przychodzi obwód prostownika. Prosta dioda złączowa PN działa jako prostownik. Warunki polaryzacji do przodu i do tyłu diody powodują prostowanie.

Sprostowanie

Prąd przemienny ma właściwość ciągłej zmiany swojego stanu. Można to zrozumieć, obserwując falę sinusoidalną, przez którą wskazywany jest prąd przemienny. Podnosi się w swoim dodatnim kierunku, przechodzi do szczytowej wartości dodatniej, stamtąd zmniejsza się do normalnej i ponownie przechodzi do części ujemnej i osiąga ujemny szczyt i ponownie wraca do normy i kontynuuje.

Podczas swojej podróży w formowaniu się fali, możemy zaobserwować, że fala biegnie w kierunku dodatnim i ujemnym. W rzeczywistości zmienia się całkowicie i stąd nazwa prąd przemienny.

Ale podczas procesu prostowania ten prąd przemienny jest zamieniany na prąd stały DC. Fala, która do tej pory płynie zarówno w kierunku dodatnim, jak i ujemnym, po konwersji na prąd stały będzie miała swój kierunek ograniczony tylko do kierunku dodatniego. W związku z tym prąd może płynąć tylko w kierunku dodatnim i opiera się w kierunku ujemnym, tak jak na poniższym rysunku.

Obwód, który wykonuje prostowanie, nazywany jest a Rectifier circuit. Dioda służy jako prostownik do budowy obwodu prostownika.

Rodzaje obwodów prostownika

Istnieją dwa główne typy obwodów prostownika, w zależności od ich mocy wyjściowej. Oni są

Prostownik półfalowy
Prostownik pełnookresowy

Obwód prostownika półokresowego prostuje tylko dodatnie półcykle zasilania wejściowego, podczas gdy obwód prostownika pełnookresowego prostuje zarówno dodatnie, jak i ujemne półcykle zasilania wejściowego.

Prostownik półfalowy

Sama nazwa prostownika półfalowego stwierdza, że rectification jest zrobione tylko dla halfcyklu. Sygnał AC jest podawany przez transformator wejściowy, który zwiększa lub zmniejsza się w zależności od zastosowania. W obwodach prostowników stosowany jest przeważnie transformator obniżający napięcie, aby zmniejszyć napięcie wejściowe.

Sygnał wejściowy podawany do transformatora przechodzi przez diodę złączową PN, która działa jak prostownik. Ta dioda przekształca napięcie przemienne w pulsujący prąd stały tylko dla dodatnich półcykli na wejściu. Rezystor obciążający jest podłączony na końcu obwodu. Poniższy rysunek przedstawia obwód prostownika półokresowego.

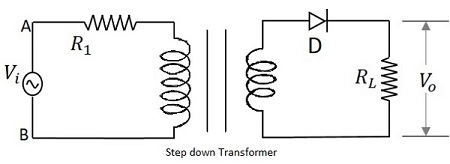
Działanie HWR

T Sygnał wejściowy podawany jest do transformatora, co zmniejsza poziomy napięcia. Sygnał wyjściowy z transformatora podawany jest na diodę, która pełni rolę prostownika. Ta dioda zapala się (przewodzi) dla dodatnich półcykli sygnału wejściowego. Stąd w obwodzie płynie prąd i nastąpi spadek napięcia na rezystorze obciążenia. Dioda wyłącza się (nie przewodzi) dla ujemnych pół cykli, a zatem wyjście dla ujemnych pół cykli będzie wynosić, $ i_ {D} = 0 $ i $ V_ {o} = 0 $.

Stąd wyjście jest obecne tylko dla dodatnich półcyklów napięcia wejściowego (pomijając zwrotny prąd upływu). To wyjście będzie pulsować, które jest przenoszone przez rezystor obciążenia.

Przebiegi HWR

Przebiegi wejściowe i wyjściowe są pokazane na poniższym rysunku.

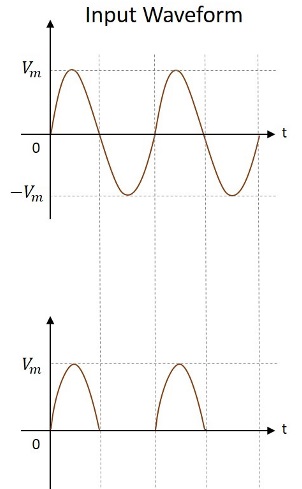
Stąd wyjście prostownika półfalowego to pulsujący prąd stały. Spróbujmy przeanalizować powyższy obwód, rozumiejąc kilka wartości, które są uzyskiwane z wyjścia prostownika półokresowego.

Analiza prostownika półfalowego

Aby przeanalizować obwód prostownika półfalowego, rozważmy równanie napięcia wejściowego.

$$ v_ {i} = V_ {m} \ sin \ omega t $$

$ V_ {m} $ to maksymalna wartość napięcia zasilania.

Załóżmy, że dioda jest idealna.

Opór w kierunku do przodu, czyli w stanie ON, wynosi $ R_f $.
Opór w odwrotnym kierunku, tj. W stanie WYŁĄCZONY, wynosi $ R_r $.

Obecny i w diodzie lub rezystorze obciążenia $ R_L $ jest podane przez

$ i = I_m \ sin \ omega t \ quad for \ quad 0 \ leq \ omega t \ leq 2 \ pi $

$ i = 0 \ quad \ quad \ quad \ quad dla \ quad \ pi \ leq \ omega t \ leq 2 \ pi $

Gdzie

$$ I_m = \ frac {V_m} {R_f + R_L} $$

Prąd wyjściowy DC

Średni bieżący $ I_ {dc} $ jest podany przez

$$ I_ {dc} = \ frac {1} {2 \ pi} \ int_ {0} ^ {2 \ pi} i \: d \ left (\ omega t \ right) $$

$$ = \ frac {1} {2 \ pi} \ left [\ int_ {0} ^ {\ pi} I_m \ sin \ omega t \: d \ left (\ omega t \ right) + \ int_ {0} ^ {2 \ pi} 0 \: d \ left (\ omega t \ right) \ right] $$

$$ = \ frac {1} {2 \ pi} \ left [I_m \ left \ {- \ cos \ omega t \ right \} _ {0} ^ {\ pi} \ right] $$

$$ = \ frac {1} {2 \ pi} \ left [I_m \ left \ {+ 1- \ left (-1 \ right) \ right \} \ right] = \ frac {I_m} {\ pi} = 0,318 I_m $$

Zastępując wartość $ I_m $, otrzymujemy

$$ I_ {dc} = \ frac {V_m} {\ pi \ left (R_f + R_L \ right)} $$

Jeśli $ R_L >> R_f $, to

$$ I_ {dc} = \ frac {V_m} {\ pi R_L} = 0,318 \ frac {V_m} {R_L} $$

Napięcie wyjściowe DC

Napięcie wyjściowe DC jest podane przez

$$ V_ {dc} = I_ {dc} \ times R_L = \ frac {I_m} {\ pi} \ times R_L $$

$$ = \ frac {V_m \ times R_L} {\ pi \ left (R_f + R_L \ right)} = \ frac {V_m} {\ pi \ left \ {1+ \ left (R_f / R_L \ right) \ right) \}} $$

Jeśli $ R_L >> R_f $, to

$$ V_ {dc} = \ frac {V_m} {\ pi} = 0,318 V_m $$

Prąd i napięcie RMS

Wartość prądu RMS jest podana przez

$$ I_ {rms} = \ left [\ frac {1} {2 \ pi} \ int_ {0} ^ {2 \ pi} i ^ {2} d \ left (\ omega t \ right) \ right] ^ {\ frac {1} {2}} $$

$$ I_ {rms} = \ left [\ frac {1} {2 \ pi} \ int_ {0} ^ {2 \ pi} I_ {m} ^ {2} \ sin ^ {2} \ omega t \: d \ left (\ omega t \ right) + \ frac {1} {2 \ pi} \ int _ {\ pi} ^ {2 \ pi} 0 \: d \ left (\ omega t \ right) \ right] ^ {\ frac {1} {2}} $$

$$ = \ left [\ frac {I_ {m} ^ {2}} {2 \ pi} \ int_ {0} ^ {\ pi} \ left (\ frac {1- \ cos 2 \ omega t} {2 } \ right) d \ left (\ omega t \ right) \ right] ^ {\ frac {1} {2}} $$

$$ = \ left [\ frac {I_ {m} ^ {2}} {4 \ pi} \ left \ {\ left (\ omega t \ right) - \ frac {\ sin 2 \ omega t} {2} \ right \} _ {0} ^ {\ pi} \ right] ^ {\ frac {1} {2}} $$

$$ = \ left [\ frac {I_ {m} ^ {2}} {4 \ pi} \ left \ {\ pi - 0 - \ frac {\ sin 2 \ pi} {2} + \ sin 0 \ right \} \ right] ^ {\ frac {1} {2}} $$

$$ = \ left [\ frac {I_ {m} ^ {2}} {4 \ pi} \ right] ^ {\ frac {1} {2}} = \ frac {I_m} {2} $$

$$ = \ frac {V_m} {2 \ left (R_f + R_L \ right)} $$

Napięcie RMS na obciążeniu wynosi

$$ V_ {rms} = I_ {rms} \ times R_L = \ frac {V_m \ times R_L} {2 \ left (R_f + R_L \ right)} $$

$$ = \ frac {V_m} {2 \ left \ {1+ \ left (R_f / R_L \ right) \ right \}} $$

Jeśli $ R_L >> R_f $, to

$$ V_ {rms} = \ frac {V_m} {2} $$

Sprawność prostownika

Aby uzyskać lepszą wydajność, każdy obwód musi działać wydajnie. Aby obliczyć sprawność prostownika półfalowego, należy wziąć pod uwagę stosunek mocy wyjściowej do mocy wejściowej.

Sprawność prostownika określa się jako

$$ \ eta = \ frac {dcpower \: \: dostarczone \: \: do \: \: \: \: load} {acinput \: \: power \: \: from \: \: transformer \: \ : secondary} = \ frac {P_ {ac}} {P_ {dc}} $$

Teraz

$$ P_ {dc} = \ left ({I_ {dc}} \ right) ^ 2 \ times R_L = \ frac {I_m R_L} {\ pi ^ 2} $$

Dalej

$$ P_ {ac} = P_a + P_r $$

Gdzie

$ P_a = moc \: rozproszone \: w \: \: skrzyżowaniu \: \: diodzie $

$$ = I_ {rms} ^ {2} \ times R_f = \ frac {I_ {m} ^ {2}} {4} \ times R_f $$

$$ P_r = moc \: rozproszone \: w \: \: obciążeniu \: oporze $$

$$ = I_ {rms} ^ {2} \ times R_L = \ frac {I_ {m} ^ {2}} {4} \ times R_L $$

$$ P_ {ac} = \ frac {I_ {m} ^ {2}} {4} \ times R_f + \ frac {I_ {m} ^ {2}} {4} \ times R_L = \ frac {I_ {m } ^ {2}} {4} \ left (R_f + R_L \ right) $$

Z obu wyrażeń $ P_ {ac} $ i $ P_ {dc} $ możemy napisać

$$ \ eta = \ frac {I_ {m} ^ {2} R_L / \ pi ^ 2} {I_ {m} ^ {2} \ left (R_f + R_L \ right) / 4} = \ frac {4} {\ pi ^ 2} \ frac {R_L} {\ left (R_f + R_L \ right)} $$

$$ = \ frac {4} {\ pi ^ 2} \ frac {1} {\ left \ {1+ \ left (R_f / R_L \ right) \ right \}} = \ frac {0.406} {\ left \ {1+ \ left (R_f / R_L \ right) \ right \}} $$

Procentowa sprawność prostownika

$$ \ eta = \ frac {40.6} {\ lbrace1 + \ lgroup \: R_ {f} / R_ {L} \ rgroup \ rbrace} $$

Teoretycznie maksymalna wartość sprawności prostownika prostownika półfalowego wynosi 40,6%, gdy $ R_ {f} / R_ {L} = 0 $

Ponadto sprawność można obliczyć w następujący sposób

$$ \ eta = \ frac {P_ {dc}} {P_ {ac}} = \ frac {\ left (I_ {dc} \ right) ^ 2R_L} {\ left (I_ {rms} \ right) ^ 2R_L} = \ frac {\ left (V_ {dc} / R_L \ right) ^ 2R_L} {\ left (V_ {rms} / R_L \ right) ^ 2R_L} = \ frac {\ left (V_ {dc} \ right) ^ 2} {\ left (V_ {rms} \ right) ^ 2} $$

$$ = \ frac {\ left (V_m / \ pi \ right) ^ 2} {\ left (V_m / 2 \ right) ^ 2} = \ frac {4} {\ pi ^ 2} = 0,406 $$

$$ = 40,6 \% $$

Ripple Factor

Wyjście wyprostowane zawiera pewną ilość obecnego w nim składnika AC w postaci tętnień. Można to zrozumieć, obserwując przebieg wyjściowy prostownika półokresowego. Aby uzyskać czysty prąd stały, musimy mieć pomysł na ten element.

Współczynnik tętnienia określa falistość wyprostowanej mocy. Jest oznaczonyy. Można to zdefiniować jako stosunek wartości skutecznej składowej AC napięcia lub prądu do wartości stałej lub wartości średniej.

$$ \ gamma = \ frac {tętnienie \: napięcie} {dc \: napięcie} = \ frac {rms \: wartość \: of \: akompaniator} {dcvalue \: of \: wave} = \ frac {\ left ( V_r \ right) _ {rms}} {v_ {dc}} $$

Tutaj,

$$ \ left (V_r \ right) _ {rms} = \ sqrt {V_ {rms} ^ {2} -V_ {dc} ^ {2}} $$

W związku z tym,

$$ \ gamma = \ frac {\ sqrt {V_ {rms} ^ {2} -V_ {dc} ^ {2}}} {V_ {dc}} = \ sqrt {\ left (\ frac {V_ {rms} } {V_ {dc}} \ right) ^ 2-1} $$

Teraz,

$$ V_ {rms} = \ left [\ frac {1} {2 \ pi} \ int_ {0} ^ {2 \ pi} V_ {m} ^ {2} \ sin ^ 2 \ omega t \: d \ left (\ omega t \ right) \ right] ^ {\ frac {1} {2}} $$

$$ = V_m \ left [\ frac {1} {4 \ pi} \ int_ {0} ^ {\ pi} \ left (1- \ cos2 \: \ omega t \ right) d \ left (\ omega t \ right) \ right] ^ {\ frac {1} {2}} = \ frac {V_m} {2} $$

$$ V_ {dc} = V_ {av} = \ frac {1} {2 \ pi} \ left [\ int_ {0} ^ {\ pi} V_m \ sin \ omega t \: d \ left (\ omega t \ right) + \ int_ {0} ^ {2 \ pi} 0.d \ left (\ omega t \ right) \ right] $$

$$ = \ frac {V_m} {2 \ pi} \ left [- \ cos \ omega t \ right] _ {0} ^ {\ pi} = \ frac {V_m} {\ pi} $$

$$ \ gamma = \ sqrt {\ left [\ left \ {\ frac {\ left (V_m / 2 \ right)} {\ left (V_m / \ pi \ right)} \ right \} ^ 2-1 \ right ]} = \ sqrt {\ left \ {\ left (\ frac {\ pi} {2} \ right) ^ 2-1 \ right \}} = 1,21 $$

Współczynnik tętnienia jest również definiowany jako

$$ \ gamma = \ frac {\ left (I_r \ right) _ {rms}} {I_ {dc}} $$

Ponieważ wartość współczynnika tętnienia obecnego w prostowniku półfalowym wynosi 1,21, oznacza to, że ilość prądu przemiennego obecnego na wyjściu wynosi 121 $ \% $ napięcia stałego

Rozporządzenie

Prąd przepływający przez obciążenie może się różnić w zależności od rezystancji obciążenia. Ale nawet w takich warunkach spodziewamy się, że nasze napięcie wyjściowe, które jest przenoszone na ten rezystor obciążenia, będzie stałe. Tak więc nasze napięcie musi być regulowane nawet przy różnych warunkach obciążenia.

Zmiana napięcia wyjściowego DC wraz ze zmianą prądu obciążenia DC jest definiowana jako Regulation. Regulacja procentowa jest obliczana w następujący sposób.

$$ Percentage \: Regulation = \ frac {V_ {no \: load} -V_ {full \: load}} {V_ {full \: load}} \ times 100 \% $$

Im niższa regulacja procentowa, tym lepsze byłoby zasilanie. Idealny zasilacz będzie miał zerową regulację procentową.

Współczynnik wykorzystania transformatora

Moc prądu stałego dostarczana do obciążenia w obwodzie prostownika decyduje o wartości znamionowej transformatora zastosowanego w obwodzie.

Tak więc współczynnik wykorzystania transformatora jest zdefiniowany jako

$$ TUF = \ frac {dcpower \: to \: be \: dostarczone \: do \: the \: load} {acrating \: of \: the \: transformer \: secondary} $$

$$ = \ frac {P_ {dc}} {P_ {ac \ left (ocenione \ right)}} $$

Zgodnie z teorią transformatora napięcie znamionowe uzwojenia wtórnego będzie wynosić

$$ V_m / \ sqrt {2} $$

Rzeczywiste napięcie RMS przepływające przez niego będzie

$$ I_m / 2 $$

W związku z tym

$$ TUF = \ frac {\ left (I_m / \ pi \ right) ^ 2 \ times R_L} {\ left (V_m / \ sqrt {2} \ right) \ times \ left (I_m / 2 \ right)} $ $

Ale

$$ V_m = I_m \ left (R_f + R_L \ right) $$

W związku z tym

$$ TUF = \ frac {\ left (I_m / \ pi \ right) ^ 2 \ times R_L} {\ left \ {I_m \ left (R_f + R_L \ right) / \ sqrt {2} \ right \} \ times \ left (I_m / 2 \ right)} $$

$$ = \ frac {2 \ sqrt {2}} {\ pi ^ 2} \ times \ frac {R_L} {\ left (R_f + R_L \ right)} $$

$$ = \ frac {2 \ sqrt {2}} {\ pi ^ 2} = 0,287 $$

Szczytowe napięcie odwrotne

Dioda, gdy jest podłączona odwrotnie, powinna pracować pod kontrolowanym poziomem napięcia. Jeśli to bezpieczne napięcie zostanie przekroczone, dioda zostanie uszkodzona. Dlatego bardzo ważne jest, aby wiedzieć o tym maksymalnym napięciu.

Maksymalne napięcie odwrotne, które dioda może wytrzymać bez zniszczenia, nazywa się Peak Inverse Voltage. W skrócie,PIV.

Tutaj PIV to nic innego jak Vm

Form Factor

Można to rozumieć jako matematyczną średnią wartości bezwzględnych wszystkich punktów na przebiegu. Plikform factordefiniuje się jako stosunek wartości RMS do wartości średniej. Jest oznaczonyF.

$$ F = \ frac {rms \: value} {średnia \: wartość} = \ frac {I_m / 2} {I_m / \ pi} = \ frac {0,5I_m} {0,318I_m} = 1,57 $$

Peak Factor

Należy wziąć pod uwagę wartość piku w tętnieniu, aby wiedzieć, jak skuteczna jest rektyfikacja. Ważną kwestią jest również wartość współczynnika szczytowego.Peak factor definiuje się jako stosunek wartości szczytowej do wartości skutecznej.

W związku z tym

$$ Peak Factor = \ frac {Peak \: value} {rms \: value} = \ frac {V_m} {V_m / 2} = 2 $$

Są to wszystkie ważne parametry, które należy wziąć pod uwagę podczas studiowania prostownika.