Specjalne funkcje LPF i HPF

Obwody filtrów dolnoprzepustowych i górnoprzepustowych są używane jako obwody specjalne w wielu zastosowaniach. Filtr dolnoprzepustowy (LPF) może działać jakoIntegrator, podczas gdy filtr górnoprzepustowy (HPF) może działać jako Differentiator. Te dwie funkcje matematyczne są możliwe tylko w przypadku tych obwodów, które zmniejszają wysiłek inżyniera elektronika w wielu zastosowaniach.

Filtr dolnoprzepustowy jako integrator

Przy niskich częstotliwościach reaktancja pojemnościowa staje się nieskończona, a przy wysokich częstotliwościach reaktancja staje się zerowa. Stąd przy niskich częstotliwościach LPF ma skończoną moc wyjściową, a przy wysokich częstotliwościach wyjście jest zerowe, co jest takie samo dla obwodu integratora. Stąd można powiedzieć, że filtr dolnoprzepustowy działa jakointegrator.

Aby LPF zachowywał się jak integrator

$$ \ tau \ gg T $$

Gdzie $ \ tau = RC $ stała czasowa obwodu

Wtedy zmiana napięcia w C jest bardzo mała.

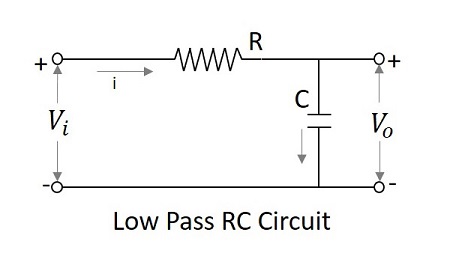
$$ V_ {i} = iR + \ frac {1} {C} \ int i \: dt $$

$$ V_ {i} \ cong iR $$

$$ Od \: \: \ frac {1} {C} \ int i \: dt \ ll iR $$

$$ i = \ frac {V_ {i}} {R} $$

$$ Ponieważ \: \: V_ {0} = \ frac {1} {C} \ int i dt = \ frac {1} {RC} \ int V_ {i} dt = \ frac {1} {\ tau} \ int V_ {i} dt $$

$$ Wyjście \ propto \ int input $$

Stąd LPF o dużej stałej czasowej wytwarza sygnał wyjściowy, który jest proporcjonalny do całki wejścia.

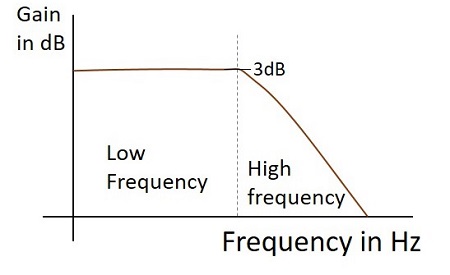
Pasmo przenoszenia

Odpowiedź częstotliwościowa praktycznego filtra dolnoprzepustowego, gdy działa jako integrator, jest taka, jak pokazano poniżej.

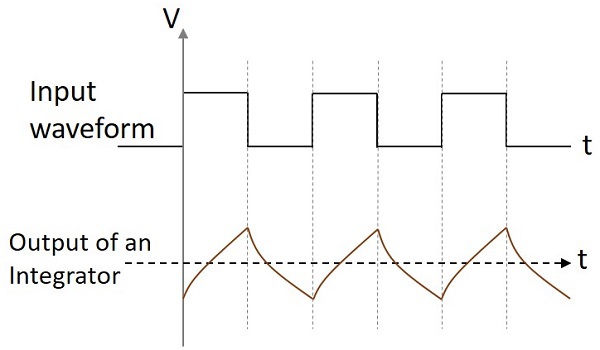
Przebieg wyjściowy

Jeśli obwód integratora ma wejście sinusoidalne, na wyjściu będzie przebieg cosinusoidalny. Jeśli wejście jest prostokątne, przebieg wyjściowy zmienia swój kształt i wygląda jak na poniższym rysunku.

Filtr górnoprzepustowy jako element różnicowy

Przy niskich częstotliwościach sygnał wyjściowy wyróżniacza wynosi zero, podczas gdy przy wysokich częstotliwościach jego sygnał wyjściowy ma pewną skończoną wartość. To jest to samo, co dla wyróżnika. Stąd mówi się, że filtr górnoprzepustowy zachowuje się jak element różnicowy.

Jeżeli stała czasowa RC HPF jest znacznie mniejsza niż okres czasu sygnału wejściowego, wówczas obwód zachowuje się jak element różniczkujący. Wtedy spadek napięcia na R jest bardzo mały w porównaniu ze spadkiem na C.

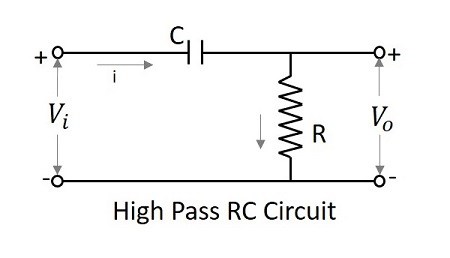
$$ V_ {i} = \ frac {1} {C} \ int i \: dt + iR $$

Ale $ iR = V_ {0} $ jest małe

$$ od V_ {i} = \ frac {1} {C} \ int i \: dt $$

$$ i = \ frac {V_ {0}} {R} $$

$$ Ponieważ \: V_ {i} = \ frac {1} {\ tau} \ int V_ {0} \: dt $$

Gdzie $ \ tau = RC $ stała czasowa obwodu.

Różnicowanie po obu stronach,

$$ \ frac {dV_ {i}} {dt} = \ frac {V_0} {\ tau} $$

$$ V_ {0} = \ tau \ frac {dV_ {i}} {dt} $$

$$ Od \: V_ {0} \ propto \ frac {dV_ {i}} {dt} $$

Wyjście jest proporcjonalne do różnicy sygnału wejściowego.

Pasmo przenoszenia

Odpowiedź częstotliwościowa praktycznego filtra górnoprzepustowego, gdy działa jako różnicowy, jest pokazana poniżej.

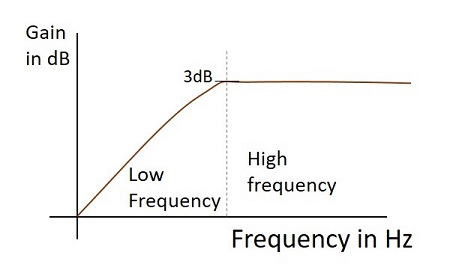
Forma fali wyjściowej

Jeśli obwód różniczkujący ma wejście sinusoidalne, na wyjściu będzie przebieg cosinusoidalny. Jeśli wejście jest prostokątne, kształt fali wyjściowej zmienia swój kształt i wygląda jak na poniższym rysunku.

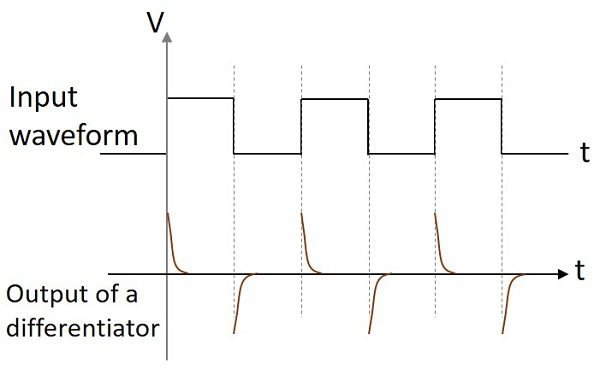
Te dwa obwody są najczęściej używane w różnych zastosowaniach elektronicznych. Obwód różnicowy wytwarza stałe napięcie wyjściowe, gdy stosowane wejście ma tendencję do stabilnej zmiany. Obwód integratora wytwarza stale zmieniające się napięcie wyjściowe, gdy przyłożone napięcie wejściowe jest stałe.