Woltomierze DC
Woltomierz prądu stałego to przyrząd pomiarowy służący do pomiaru napięcia prądu stałego w dowolnych dwóch punktach obwodu elektrycznego. Jeśli umieścimy rezystor szeregowo z galwanometrem z ruchomą cewką z magnesem trwałym (PMMC), to cała kombinacja razem działa jakDC voltmeter.
Rezystancja szeregowa, która jest używana w woltomierzu prądu stałego, jest również nazywana rezystancją mnożnika szeregowego lub po prostu mnożnikiem. Zasadniczo ogranicza ilość prądu przepływającego przez galwanometr, aby zapobiec przekroczeniu przez prąd miernika wartości odchylenia pełnej skali. Plikcircuit diagram woltomierza prądu stałego pokazano na poniższym rysunku.
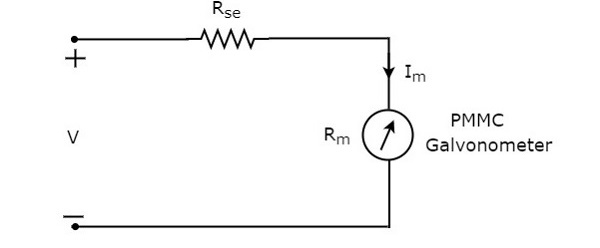
Musimy umieścić ten woltomierz prądu stałego między dwoma punktami obwodu elektrycznego, w których ma być mierzone napięcie prądu stałego.
Zastosować KVL wokół pętli powyższego obwodu.
$ V-I_ {m} R_ {se} -I_ {m} R_ {m} = 0 $ (równanie 1)
$$ \ Rightarrow V-I_ {m} R_ {m} = I_ {m} R_ {se} $$
$$ \ Rightarrow R_ {se} = \ frac {V-I_ {m} R_ {m}} {I_ {m}} $$
$ \ Rightarrow R_ {se} = \ frac {V} {I_ {m}} - R_ {m} $ (Równanie 2)
Gdzie,
$ R_ {se} $ jest oporem mnożnika serii
$ V $ to mierzone napięcie prądu stałego w pełnym zakresie
$ I_ {m} $ jest prądem odchylającym w pełnej skali
$ R_ {m} $ jest oporem wewnętrznym galwanometru
Stosunek mierzonego napięcia stałego w pełnym zakresie, $ V $, i spadku napięcia prądu stałego na galwanometrze, $ V_ {m} $, jest znany jako multiplying factor, m. Matematycznie można to przedstawić jako
$ m = \ frac {V} {V_ {m}} $ (równanie 3)
Z równania 1 otrzymamy następujące równanie dla full range DC voltage to ma być zmierzone, $ V $.
$ V = I_ {m} R_ {se} + I_ {m} R_ {m} $ (Równanie 4)
Plik DC voltage dropw poprzek galwanometru, $ V_ {m} $ jest iloczynem prądu odchylania w pełnej skali, $ I_ {m} $ i oporu wewnętrznego galwanometru, $ R_ {m} $. Matematycznie można to zapisać jako
$ V_ {m} = I_ {m} R_ {m} $ (Równanie 5)
Substitute, Równanie 4 i Równanie 5 w równaniu 3.
$$ m = \ frac {I_ {m} R_ {se} + I_ {m} R_ {m}} {I_ {m} R_ {m}} $$
$ \ Rightarrow m = \ frac {R_ {se}} {R_ {m}} + 1 $
$ \ Rightarrow m-1 = \ frac {R_ {se}} {R_ {m}} $
$ R_ {se} = R_ {m} \ left (m-1 \ right) $ (Równanie 6)
Możemy znaleźć value of series multiplier resistance korzystając z równania 2 lub równania 6 w oparciu o dostępne dane.
Wielozakresowy woltomierz DC
W poprzednim rozdziale omówiliśmy woltomierz prądu stałego, który uzyskuje się poprzez szeregowe umieszczenie rezystora powielającego z galwanometrem PMMC. Ten woltomierz prądu stałego może być używany do pomiaru aparticular range napięć DC.
Jeśli chcemy użyć woltomierza prądu stałego do pomiaru napięcia stałego o wartości multiple ranges, wtedy musimy użyć wielu równoległych rezystorów powielających zamiast pojedynczego rezystora powielającego, a cała ta kombinacja rezystorów jest połączona szeregowo z galwanometrem PMMC. Plikcircuit diagram wielozakresowego woltomierza prądu stałego pokazano na poniższym rysunku.
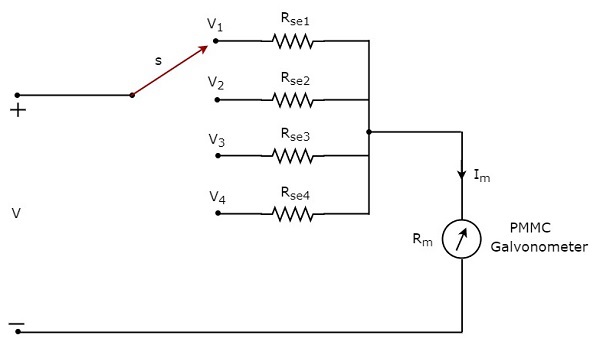
Musimy to umieścić multi range DC voltmeterw dwóch punktach obwodu elektrycznego, w których ma być mierzone napięcie prądu stałego o wymaganym zakresie. Żądany zakres napięć możemy wybrać podłączając przełącznik s do odpowiedniego rezystora powielającego.
Niech, $ m_ {1}, m_ {2}, m_ {2} $ i $ m_ {4} $ są multiplying factorswoltomierza prądu stałego, gdy rozważymy mierzone napięcia prądu stałego w pełnym zakresie jako odpowiednio $ V_ {1}, V_ {2}, V_ {3} $ i $ V_ {4} $. Poniżej znajdują się wzory odpowiadające każdemu mnożnikowi.
$$ m_ {1} = \ frac {V_ {1}} {V_ {m}} $$
$$ m_ {2} = \ frac {V_ {2}} {V_ {m}} $$
$$ m_ {3} = \ frac {V_ {3}} {V_ {m}} $$
$$ m_ {4} = \ frac {V_ {4}} {V_ {m}} $$
W powyższym obwodzie są cztery series multiplier resistors, $ R_ {se1}, R_ {se2}, R_ {se3} $ i $ R_ {se4} $. Poniżej znajdują się wzory odpowiadające tym czterem rezystorom.
$$ R_ {se1} = R_ {m} \ left (m_ {1} -1 \ right) $$
$$ R_ {se2} = R_ {m} \ left (m_ {2} -1 \ right) $$
$$ R_ {se3} = R_ {m} \ left (m_ {3} -1 \ right) $$
$$ R_ {se4} = R_ {m} \ left (m_ {4} -1 \ right) $$
Tak więc możemy znaleźć wartości rezystancji każdego rezystora mnożącego szeregowego za pomocą powyższych wzorów.