Szybka porada

Przyrządy używane do pomiaru dowolnej wielkości nazywane są przyrządami pomiarowymi. Ten samouczek obejmuje głównieelectronic instruments, które są przydatne do pomiaru wielkości lub parametrów elektrycznych.

Poniżej przedstawiono najczęściej używane instrumenty elektroniczne.

• Voltmeter
• Ammeter
• Ohmmeter
• Multimeter

Omówmy teraz pokrótce te instrumenty.

Woltomierz

Jak sama nazwa wskazuje, voltmeterto przyrząd pomiarowy, który mierzy napięcie w dowolnych dwóch punktach obwodu elektrycznego. Istnieją dwa typy woltomierzy: woltomierz prądu stałego i woltomierz prądu przemiennego.

Woltomierz prądu stałego mierzy napięcie prądu stałego w dowolnych dwóch punktach obwodu elektrycznego, natomiast woltomierz prądu przemiennego mierzy napięcie prądu przemiennego w dowolnych dwóch punktach obwodu elektrycznego. Przykładpractical DC voltmeter pokazano na poniższym rysunku.

Woltomierz DC pokazany na powyższym rysunku to $(0-100)V$ DC voltmeter. W związku z tym może być używany do pomiaru napięcia stałego od zera do 10 woltów.

Amperomierz

Jak sama nazwa wskazuje, ammeterto przyrząd pomiarowy, który mierzy prąd płynący przez dowolne dwa punkty obwodu elektrycznego. Istnieją dwa typy amperomierzy: amperomierz DC i amperomierz AC.

Amperomierz prądu stałego mierzy prąd stały przepływający przez dowolne dwa punkty obwodu elektrycznego. Natomiast amperomierz prądu przemiennego mierzy prąd przemienny przepływający przez dowolne dwa punkty obwodu elektrycznego. Przykładpractical AC ammeter pokazano na poniższym rysunku -

Amperomierz prądu zmiennego pokazany na powyższym rysunku to $(0-100)A \:$ AC ammeter. W związku z tym może być używany do pomiaru prądów AC od zera amperów do 100 amperów.

Omomierz

Ohmmetersłuży do pomiaru wartości rezystancji między dowolnymi dwoma punktami obwodu elektrycznego. Można go również użyć do znalezienia wartości nieznanego rezystora. Istnieją dwa rodzaje omomierzy: omomierz szeregowy i omomierz bocznikowy.

W omomierzu szeregowym rezystor, którego wartość jest nieznana i ma być zmierzony, należy połączyć szeregowo z omomierzem. Przydaje się do pomiaruhigh values of resistances.

W omomierzu bocznikowym rezystor, którego wartość jest nieznana i ma być zmierzony, powinien być połączony równolegle (bocznik) z omomierzem. Przydaje się do pomiarulow values of resistances.

Przykład practical shunt ohmmeterpokazano na powyższym rysunku. Omomierz pokazany na powyższym rysunku to$(0-100)\Omega$ shunt ohmmeter. W związku z tym można go użyć do pomiaru wartości rezystancji od zera do 100 omów.

Multimetr

Multimeterjest przyrządem elektronicznym używanym do pomiaru wielkości, takich jak napięcie, prąd i rezystancja pojedynczo. Może być używany do pomiaru napięć DC i AC, prądów DC i AC oraz rezystancji w kilku zakresach. Praktyczny multimetr pokazano na poniższym rysunku -

Jak pokazano na rysunku, ten multimetr może być używany do pomiaru różnych wysokich rezystancji, niskich rezystancji, napięć DC, napięć AC, prądów DC i prądów AC. Na powyższym rysunku zaznaczono różne skale i zakresy wartości dla każdej z tych wielkości.

Instrumenty, które rozważaliśmy w tym rozdziale, należą indicating type instruments, ponieważ wskaźniki tych instrumentów odchylają się i wskazują na określoną wartość. Omówimy szczegółowo te elektroniczne przyrządy pomiarowe w dalszych rozdziałach.

Charakterystyki przyrządów pomiarowych, które pomagają poznać działanie przyrządu i pomagają w pomiarze dowolnej wielkości lub parametru, są znane jako Performance Characteristics.

Rodzaje cech wykonawczych

Charakterystykę działania instrumentów można podzielić na następujące two types.

• Charakterystyka statyczna
• Charakterystyka dynamiczna

Omówmy teraz kolejno te dwa typy cech.

Charakterystyka statyczna

Charakterystyka wielkości lub parametrów przyrządów pomiarowych, które do not varywzględem czasu nazywane są charakterystyką statyczną. Czasami te wielkości lub parametry mogą zmieniać się powoli w czasie. Poniżej znajduje się listastatic characteristics.

• Accuracy
• Precision
• Sensitivity
• Resolution
• Błąd statyczny

Omówmy teraz kolejno te statyczne cechy.

Precyzja

Różnica algebraiczna między wskazaną wartością instrumentu, $A_{i}$ i prawdziwą wartość, $A_{t}$ jest znany jako accuracy. Matematycznie można to przedstawić jako -

$$Accuracy = A_{i}- A_{t}$$

Termin dokładność oznacza, jak bardzo wskazana wartość instrumentu, $A_{i}$ jest bliższa prawdziwej wartości, $A_{t}$.

Błąd statyczny

Różnica między prawdziwą wartością, $A_{t}$ o niezmiennej w czasie ilości i wskazanej wartości instrumentu, $A_{i}$ jest znany jako static error, $e_{s}$. Matematycznie można to przedstawić jako -

$$e_{s}= A_{t}- A_{i}$$

Termin, błąd statyczny oznacza niedokładność instrumentu. Jeśli błąd statyczny jest reprezentowany w procentach, jest wywoływanypercentage of static error. Matematycznie można to przedstawić jako -

$$\% e_{s}=\frac{e_{s}}{A_{t}}\times 100$$

Zastąpienie, wartość $e_{s}$ po prawej stronie powyższego równania -

$$\% e_{s}=\frac{A_{t}- A_{i}}{A_{t}}\times 100$$

Gdzie,

$\% e_{s}$ to procent błędu statycznego.

Precyzja

Jeśli instrument wskazuje tę samą wartość wielokrotnie, gdy jest używany do pomiaru tej samej wielkości w tych samych okolicznościach i wiele razy, możemy powiedzieć, że instrument ma wysoką precision.

Wrażliwość

Stosunek zmiany produkcji, $\Delta A_{out}$ instrumentu dla danej zmiany wejścia, $\Delta A_{in}$ to, co ma być zmierzone, nazywa się sensitivity, S. Matematycznie można to przedstawić jako -

$$S=\frac{\Delta A_{out}}{\Delta A_{in}}$$

Termin wrażliwość oznacza najmniejszą zmianę mierzalnych danych wejściowych, która jest wymagana do odpowiedzi instrumentu.

• Jeśli krzywa kalibracji to linear, wówczas czułość przyrządu będzie stała i jest równa nachyleniu krzywej kalibracji.

• Jeśli krzywa kalibracji to non-linear, wtedy czułość instrumentu nie będzie stała i będzie się zmieniać w zależności od wejścia.

Rozkład

Jeśli wynik instrumentu zmieni się tylko wtedy, gdy nastąpi określony przyrost wejścia, to ten przyrost wejścia nazywany jest Resolution. Oznacza to, że przyrząd jest w stanie efektywnie mierzyć wejście, gdy istnieje rozdzielczość wejścia.

Charakterystyka dynamiczna

Charakterystyki przyrządów, które są używane do pomiaru wielkości lub parametrów zmieniających się bardzo szybko w czasie, nazywane są charakterystykami dynamicznymi. Poniżej znajduje się listadynamic characteristics.

• Szybkość reakcji
• Błąd dynamiczny
• Fidelity
• Lag

Omówmy teraz kolejno te dynamiczne cechy.

Szybkość reakcji

Wywoływana jest szybkość, z jaką przyrząd reaguje za każdym razem, gdy następuje zmiana wielkości do pomiaru speed of response. Wskazuje, jak szybki jest instrument.

Opóźnienie

Opóźnienie występujące w odpowiedzi przyrządu za każdym razem, gdy następuje zmiana wielkości do pomiaru, nazywa się opóźnieniem pomiarowym. Jest również po prostu nazywanylag.

Błąd dynamiczny

Różnica między prawdziwą wartością, $A_{t}$ o wielkości zmieniającej się w czasie i wskazanej wartości instrumentu, $A_{i}$ jest znany jako błąd dynamiczny, $e_{d}$.

wierność

Stopień, w jakim instrument wskazuje zmiany wielkości mierzonej bez żadnego błędu dynamicznego, jest znany jako Fidelity

Błędy, które występują podczas pomiaru, nazywane są measurement errors. W tym rozdziale omówimy rodzaje błędów pomiarowych.

Rodzaje błędów pomiarowych

Możemy podzielić błędy pomiaru na następujące trzy typy.

• Poważne błędy
• Przypadkowe błędy
• Systematyczne błędy

Omówmy teraz kolejno te trzy typy błędów pomiarowych.

Poważne błędy

Błędy, które pojawiają się z powodu braku doświadczenia obserwatora przy dokonywaniu pomiarów, nazywane są gross errors. Wartości poważnych błędów będą się różnić w zależności od obserwatora. Czasami mogą wystąpić poważne błędy z powodu niewłaściwego doboru instrumentu. Możemy zminimalizować poważne błędy, wykonując te dwa kroki.

• Wybierz najlepszy odpowiedni przyrząd na podstawie zakresu mierzonych wartości.
• Zanotuj uważnie odczyty

Systematyczne błędy

Jeśli przyrząd generuje błąd polegający na stałym, jednolitym odchyleniu podczas pracy, nazywany jest systematic error. Systematyczne błędy wynikają z właściwości materiałów użytych w przyrządzie.

Types of Systematic Errors

Błędy systematyczne można podzielić na następujące three types.

• Instrumental Errors - Tego typu błędy pojawiają się z powodu wad instrumentów i efektów ładowania.

• Environmental Errors - Tego typu błędy pojawiają się w wyniku zmian środowiska, takich jak zmiana temperatury, ciśnienia itp.

• observational Errors - Tego typu błędy powstają z powodu obserwatora podczas odczytów licznika. Parallax errors należą do tego typu błędów.

Przypadkowe błędy

Błędy, które występują z powodu nieznanych źródeł w czasie pomiaru, są znane jako random errors. Dlatego nie jest możliwe wyeliminowanie lub zminimalizowanie tych błędów. Ale jeśli chcemy uzyskać dokładniejsze wartości pomiaru bez żadnego przypadkowego błędu, jest to możliwe, wykonując te dwa kroki.

• Step1 - Wykonaj większą liczbę odczytów przez różnych obserwatorów.

• Step2 - Wykonaj analizę statystyczną odczytów uzyskanych w kroku 1.

Poniżej przedstawiono parametry używane w analizie statystycznej.

• Mean
• Median
• Variance
• Deviation
• Odchylenie standardowe

A teraz omówmy to statistical parameters.

Oznaczać

Pozwolić $x_{1},x_{2},x_{3},....,x_{N}$ są $N$odczyty konkretnego pomiaru. Średnia lubaverage value tych odczytów można obliczyć za pomocą następującego wzoru.

$$m = \frac{x_{1}+x_{2}+x_{3}+....+x_{N}}{N}$$

Gdzie, $m$ jest wartością średnią lub średnią.

Jeśli liczba odczytów danego pomiaru jest większa, to średnia lub średnia wartość będzie w przybliżeniu równa true value

Mediana

Jeśli liczba odczytów danego pomiaru jest większa, trudno jest obliczyć średnią lub średnią wartość. Tutaj obliczmedian value i będzie w przybliżeniu równa średniej wartości.

Aby obliczyć wartość mediany, najpierw musimy ustawić odczyty konkretnego pomiaru w pliku ascending order. Możemy obliczyć medianę za pomocą następującego wzoru, gdy liczba odczytów wynosiodd number.

$$M=x_{\left ( \frac{N+1}{2} \right )}$$

Możemy obliczyć medianę za pomocą następującego wzoru, gdy liczba odczytów wynosi even number.

$$M=\frac{x_{\left ( N/2 \right )}+x_\left ( \left [ N/2 \right ]+1 \right )}{2}$$

Odchylenie od średniej

Różnica między odczytem konkretnego pomiaru a wartością średnią nazywana jest odchyleniem od średniej . Krótko mówiąc, nazywa się to odchyleniem . Matematycznie można to przedstawić jako

$$d_{i}=x_{i}-m$$

Gdzie,

$d_{i}$ to odchylenie $i^{th}$ czytanie od średniej.

$x_{i}$ jest wartością $i^{th}$ czytanie.

$m$ jest wartością średnią lub średnią.

Odchylenie standardowe

Zwana jest średnia kwadratowa odchylenia standard deviation. Matematycznie można to przedstawić jako

$$\sigma =\sqrt{\frac{{d_{1}}^{2}+{d_{2}}^{2}+{d_{3}}^{2}+....+{d_{N}}^{2}}{N}}$$

Powyższy wzór jest ważny, jeśli liczba odczytów N jest większa lub równa 20. Możemy użyć następującego wzoru na odchylenie standardowe, gdy liczba odczytów N jest mniejsza niż 20.

$$\sigma =\sqrt{\frac{{d_{1}}^{2}+{d_{2}}^{2}+{d_{3}}^{2}+....+{d_{N}}^{2}}{N-1}}$$

Gdzie,

$\sigma$ to odchylenie standardowe

$d_{1}, d_{2}, d_{3}, …, d_{N}$ są odchyleniami pierwszego, drugiego, trzeciego,…, $N^{th}$odczyty ze średniej odpowiednio.

Note - Jeśli wartość odchylenia standardowego jest mała, dokładność odczytów pomiaru będzie większa.

Zmienność

Kwadrat odchylenia standardowego to tzw variance. Matematycznie można to przedstawić jako

$$V=\sigma^{2}$$

Gdzie,

$V$ jest wariancja

$\sigma$ to odchylenie standardowe

Nazywa się również średni kwadrat odchylenia variance. Matematycznie można to przedstawić jako

$$V=\frac{{d_{1}}^{2}+{d_{2}}^{2}+{d_{3}}^{2}+....+{d_{N}}^{2}}{N}$$

Powyższy wzór jest ważny, jeśli liczba odczytów N jest większa lub równa 20. Możemy użyć następującego wzoru na wariancję, gdy liczba odczytów N jest mniejsza niż 20.

$$V=\frac{{d_{1}}^{2}+{d_{2}}^{2}+{d_{3}}^{2}+....+{d_{N}}^{2}}{N-1}$$

Gdzie,

$V$ jest wariancja

$d_{1}, d_{2}, d_{3}, …, d_{N}$ są odchyleniami pierwszego, drugiego, trzeciego,…, $N^{th}$ odczyty ze średniej odpowiednio.

Tak więc za pomocą parametrów statystycznych możemy analizować odczyty konkretnego pomiaru. W ten sposób uzyskamy dokładniejsze wartości pomiarowe.

Przyrządy używane do pomiaru dowolnej ilości są znane jako measuring instruments. Jeśli przyrządy mogą mierzyć podstawowe wielkości elektryczne, takie jak napięcie i prąd, są znane jakobasic measuring instruments.

Rodzaje podstawowych przyrządów pomiarowych

Podstawowe przyrządy pomiarowe możemy podzielić na następujące dwa typy.

• Voltmeters
• Ammeters

Omówmy pokrótce te dwa podstawowe przyrządy pomiarowe.

Woltomierze

Jak sama nazwa wskazuje, voltmeterto przyrząd pomiarowy, który mierzy napięcie w dowolnych dwóch punktach obwodu elektrycznego. Jednostkami napięcia są wolty, a przyrządem pomiarowym jest metr. Stąd słowo „woltomierz” uzyskuje się przez połączenie tych dwóch słów“volt” i “meter”.

Możemy podzielić woltomierze na następujące two types w oparciu o rodzaj napięcia, które może zmierzyć.

• Woltomierze DC
• Woltomierze AC

Woltomierz DC

Jak sama nazwa wskazuje, woltomierz DC mierzy DC voltagew dowolnych dwóch punktach obwodu elektrycznego. Praktyczny woltomierz prądu stałego pokazano na poniższym rysunku.

Woltomierz prądu stałego pokazany na rysunku to a $(0-10)V$ DC voltmeter. W związku z tym może być używany do pomiaru napięcia stałego od zera do 10 woltów

Woltomierz AC

Jak sama nazwa wskazuje, woltomierz AC mierzy AC voltagew dowolnych dwóch punktach obwodu elektrycznego. Praktyczny woltomierz AC pokazano na poniższym rysunku.

Woltomierz AC pokazany na powyższym rysunku to $(0-250)V$ AC voltmeter. W związku z tym może być używany do pomiaru napięć prądu przemiennego od zera do 250 woltów

Amperomierze

Jak sama nazwa wskazuje, ammeterto przyrząd pomiarowy, który mierzy prąd płynący przez dowolne dwa punkty obwodu elektrycznego. Jednostką prądu jest amper, a przyrządem pomiarowym jest metr. Słowo „amperomierz” uzyskuje się przez połączenie“am” amperów z “meter”.

Możemy podzielić amperomierze na następujące two types w oparciu o rodzaj prądu, który może zmierzyć.

• Amperomierze prądu stałego
• Amperomierze AC

Amperomierz prądu stałego

Jak sama nazwa wskazuje, amperomierz prądu stałego mierzy DC currentktóry przepływa przez dowolne dwa punkty obwodu elektrycznego. Praktyczny amperomierz prądu stałego pokazano na rysunku.

Amperomierz prądu stałego pokazany na powyższym rysunku to $(0-50)A$ DC ammeter. W związku z tym może być używany do pomiaru prądów stałych od zera amperów do 50 amperów

Amperomierz AC

Jak sama nazwa wskazuje, amperomierz prądu przemiennego mierzy AC currentktóry przepływa przez dowolne dwa punkty obwodu elektrycznego. Praktyczny amperomierz prądu przemiennego pokazano na poniższym rysunku.

Amperomierz prądu zmiennego pokazany na powyższym rysunku to $(0-100)A$ AC ammeter. W związku z tym może być używany do pomiaru prądów AC od zera amperów do 100 amperów.

Omówimy szczegółowo różne woltomierze i amperomierze w kilku kolejnych rozdziałach

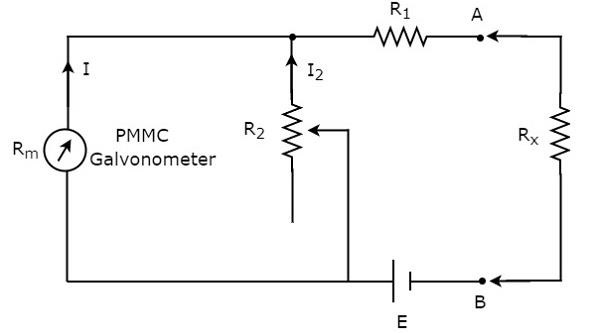
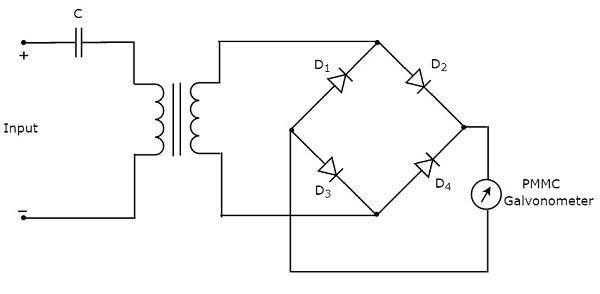
Woltomierz prądu stałego to przyrząd pomiarowy służący do pomiaru napięcia prądu stałego w dowolnych dwóch punktach obwodu elektrycznego. Jeśli umieścimy rezystor szeregowo z galwanometrem z ruchomą cewką z magnesem trwałym (PMMC), to cała kombinacja razem działa jakDC voltmeter.

Rezystancja szeregowa, która jest używana w woltomierzu prądu stałego, jest również nazywana rezystancją mnożnika szeregowego lub po prostu mnożnikiem. Zasadniczo ogranicza ilość prądu przepływającego przez galwanometr, aby zapobiec przekroczeniu przez prąd miernika wartości odchylenia pełnej skali. Plikcircuit diagram woltomierza prądu stałego pokazano na poniższym rysunku.

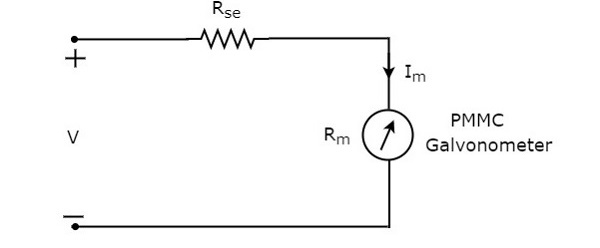
Musimy umieścić ten woltomierz prądu stałego między dwoma punktami obwodu elektrycznego, w których ma być mierzone napięcie prądu stałego.

Zastosować KVL wokół pętli powyższego obwodu.

$V-I_{m}R_{se}-I_{m}R_{m}=0$ (Równanie 1)

$$\Rightarrow V-I_{m}R_{m}=I_{m}R_{se}$$

$$\Rightarrow R_{se}=\frac{V-I_{m}R_{m}}{I_{m}}$$

$\Rightarrow R_{se}=\frac{V}{I_{m}}-R_{m}$ (Równanie 2)

Gdzie,

$R_{se}$ oznacza rezystancję mnożnika szeregu

$V$ to mierzone napięcie prądu stałego w pełnym zakresie

$I_{m}$ jest prądem odchylającym w pełnej skali

$R_{m}$ jest oporem wewnętrznym galwanometru

Stosunek mierzonego napięcia stałego w pełnym zakresie, $V$ i spadek napięcia DC na galwanometrze, $V_{m}$ jest znany jako multiplying factor, m. Matematycznie można to przedstawić jako

$m=\frac{V}{V_{m}}$ (Równanie 3)

Z równania 1 otrzymamy następujące równanie dla full range DC voltage to ma być zmierzone, $V$.

$V=I_{m}R_{se}+I_{m}R_{m}$ (Równanie 4)

Plik DC voltage drop w poprzek galwanometru, $V_{m}$ jest iloczynem prądu odchylenia w pełnej skali, $I_{m}$ i opór wewnętrzny galwanometru, $R_{m}$. Matematycznie można to zapisać jako

$V_{m}=I_{m}R_{m}$ (Równanie 5)

Substitute, Równanie 4 i Równanie 5 w równaniu 3.

$$m=\frac{I_{m}R_{se}+I_{m}R_{m}}{I_{m}R_{m}}$$

$\Rightarrow m=\frac{R_{se}}{R_{m}}+1$

$\Rightarrow m-1=\frac{R_{se}}{R_{m}}$

$R_{se}=R_{m}\left (m-1 \right )$(Równanie 6)

Możemy znaleźć value of series multiplier resistance korzystając z równania 2 lub równania 6 w oparciu o dostępne dane.

Wielozakresowy woltomierz DC

W poprzednim rozdziale omówiliśmy woltomierz prądu stałego, który uzyskuje się poprzez szeregowe umieszczenie rezystora powielającego z galwanometrem PMMC. Ten woltomierz prądu stałego może być używany do pomiaru aparticular range napięć DC.

Jeśli chcemy użyć woltomierza prądu stałego do pomiaru napięcia stałego o wartości multiple ranges, wtedy musimy użyć wielu równoległych rezystorów powielających zamiast pojedynczego rezystora powielającego, a cała ta kombinacja rezystorów jest połączona szeregowo z galwanometrem PMMC. Plikcircuit diagram wielozakresowego woltomierza prądu stałego pokazano na poniższym rysunku.

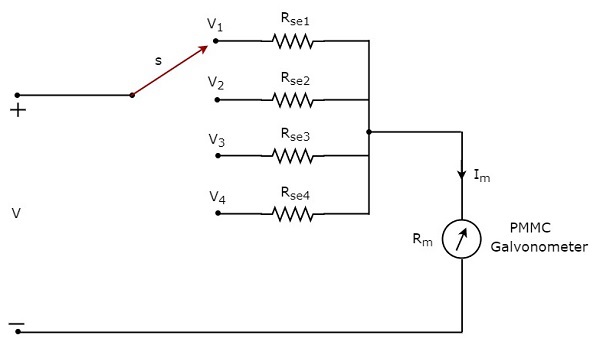
Musimy to umieścić multi range DC voltmeterw dwóch punktach obwodu elektrycznego, w których ma być mierzone napięcie prądu stałego o wymaganym zakresie. Żądany zakres napięć możemy wybrać podłączając przełącznik s do odpowiedniego rezystora powielającego.

Pozwolić, $m_{1},m_{2}, m_{2} $ i $m_{4}$ są multiplying factors woltomierza prądu stałego, gdy weźmiemy pod uwagę mierzone napięcia prądu stałego w pełnym zakresie jako: $V_{1} , V_{2}, V_{3}$ i $V_{4}$odpowiednio. Poniżej znajdują się wzory odpowiadające każdemu mnożnikowi.

$$m_{1}=\frac{V_{1}}{V_{m}}$$

$$m_{2}=\frac{V_{2}}{V_{m}}$$

$$m_{3}=\frac{V_{3}}{V_{m}}$$

$$m_{4}=\frac{V_{4}}{V_{m}}$$

W powyższym obwodzie są cztery series multiplier resistors, $R_{se1}, R_{se2}, R_{se3}$ i $R_{se4}$. Poniżej znajdują się wzory odpowiadające tym czterem rezystorom.

$$R_{se1}=R_{m}\left (m_{1}-1 \right )$$

$$R_{se2}=R_{m}\left (m_{2}-1 \right )$$

$$R_{se3}=R_{m}\left (m_{3}-1 \right )$$

$$R_{se4}=R_{m}\left (m_{4}-1 \right )$$

Tak więc możemy znaleźć wartości rezystancji każdego szeregowego rezystora mnożącego za pomocą powyższych wzorów.

Przyrząd, który służy do pomiaru napięcia AC w ​​dowolnych dwóch punktach obwodu elektrycznego, nazywa się AC voltmeter. Jeśli woltomierz prądu przemiennego składa się z prostownika, mówi się, że jest to woltomierz prądu przemiennego oparty na prostowniku.

Woltomierz DC mierzy tylko napięcia DC. Jeśli chcemy go użyć do pomiaru napięć przemiennych, musimy wykonać te dwa kroki.

• Step1 - Przekształć sygnał napięcia AC na sygnał napięcia DC za pomocą prostownika.

• Step2 - Zmierz wartość prądu stałego lub średnią wartość sygnału wyjściowego prostownika.

Dostajemy Rectifier based AC voltmeter, po prostu dołączając obwód prostownika do podstawowego woltomierza DC. Ten rozdział dotyczy woltomierzy AC opartych na prostownikach.

Rodzaje woltomierzy prądu przemiennego opartych na prostownikach

Poniżej znajdują się pliki two types woltomierzy AC z prostownikiem.

• Woltomierz prądu przemiennego wykorzystujący prostownik półfalowy
• Woltomierz prądu przemiennego wykorzystujący prostownik pełnookresowy

Omówmy teraz kolejno te dwa woltomierze prądu przemiennego.

Woltomierz prądu przemiennego wykorzystujący prostownik półfalowy

Jeśli prostownik półokresowy jest podłączony przed woltomierzem prądu stałego, to cała ta kombinacja nazywana jest woltomierzem prądu przemiennego z prostownikiem półokresowym. Plikblock diagram woltomierza AC z prostownikiem półokresowym pokazano na poniższym rysunku.

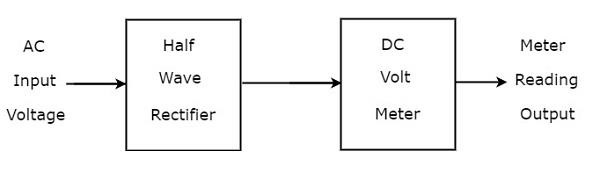
Powyższy schemat blokowy składa się z dwóch bloków: prostownika półokresowego i woltomierza prądu stałego. Otrzymamy odpowiedni schemat obwodu, po prostu zastępując każdy blok odpowiednimi komponentami z powyższego schematu blokowego. Tak więccircuit diagram woltomierza AC używającego prostownika półokresowego będzie wyglądać tak, jak pokazano na poniższym rysunku.

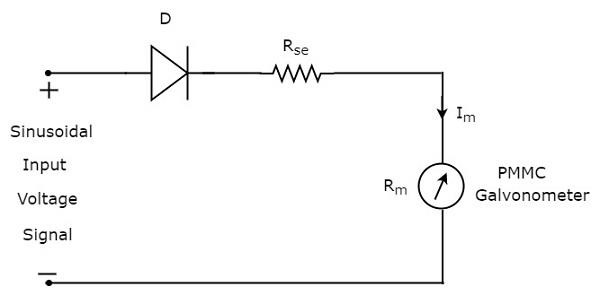
Plik rms value napięcia wejściowego sinusoidalnego (AC)

$$V_{rms}=\frac{V_{m}}{\sqrt{2}}$$

$$\Rightarrow V_{m}=\sqrt{2} V_{rms}$$

$$\Rightarrow V_{m}=1.414 V_{rms}$$

Gdzie,

$V_{m}$ jest maksymalną wartością sinusoidalnego (AC) sygnału wejściowego.

Plik DC lub średnia wartość sygnału wyjściowego prostownika półokresowego wynosi

$$V_{dc}=\frac{V_{m}}{\pi}$$

Substitute, wartość $V_{m}$ w powyższym równaniu.

$$V_{dc}= \frac{1.414 V_{rms}}{\pi}$$

$$V_{dc}= 0.45 V_{rms}$$

Dlatego woltomierz prądu przemiennego wytwarza napięcie wyjściowe, które jest równe 0.45 razy wartość skuteczna sinusoidalnego (AC) sygnału wejściowego

Woltomierz prądu przemiennego wykorzystujący prostownik pełnookresowy

Jeśli prostownik pełnookresowy jest podłączony przed woltomierzem prądu stałego, to cała ta kombinacja razem nazywana jest woltomierzem prądu przemiennego z prostownikiem pełnookresowym. Plikblock diagram woltomierza AC z prostownikiem pełnookresowym pokazano na poniższym rysunku

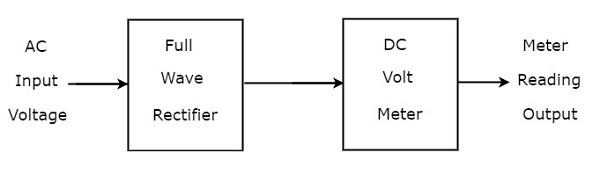
Powyższy schemat blokowy składa się z dwóch bloków: prostownika pełnookresowego i woltomierza prądu stałego. Otrzymamy odpowiedni schemat obwodu, zastępując każdy blok odpowiednimi komponentami z powyższego schematu blokowego.

Tak więc circuit diagram woltomierza AC używającego prostownika pełnookresowego będzie wyglądać tak, jak pokazano na poniższym rysunku.

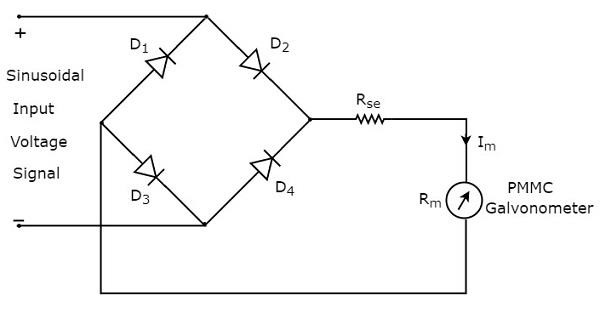
Plik rms value napięcia wejściowego sinusoidalnego (AC)

$$V_{rms}=\frac{V_{m}}{\sqrt{2}}$$

$$\Rightarrow V_{m}=\sqrt{2} \:V_{rms}$$

$$\Rightarrow V_{m}= 1.414 V_{rms}$$

Gdzie,

$V_{m}$ jest maksymalną wartością sinusoidalnego (AC) sygnału wejściowego.

Plik DC lub średnia wartość sygnału wyjściowego prostownika pełnookresowego wynosi

$$V_{dc}=\frac{2V_{m}}{\pi}$$

Substitute, wartość $V_{m}$ w powyższym równaniu

$$V_{dc}=\frac{2\times 1.414 \:V_{rms}}{\pi}$$

$$V_{dc}=0.9 \:V_{rms}$$

Dlatego woltomierz prądu przemiennego wytwarza napięcie wyjściowe, które jest równe 0.9 razy wartość skuteczna sinusoidalnego (AC) sygnału wejściowego.

W poprzednim rozdziale omówiliśmy woltomierze prądu zmiennego oparte na prostownikach. W tym rozdziale omówiono dwa typy woltomierzy prądu przemiennego.

• Woltomierz AC reagujący na wartość szczytową
• Woltomierz AC odpowiadający True RMS

Omówmy teraz kolejno te dwa typy woltomierzy prądu przemiennego.

Woltomierz AC odpowiadający wartości szczytowej

Jak sama nazwa wskazuje, reaguje na szczytowy woltomierz prądu przemiennego peak valuessygnału napięcia zmiennego. Oznacza to, że ten woltomierz mierzy wartości szczytowe napięć AC. Plikcircuit diagram woltomierza AC odpowiadającego szczytowo pokazano poniżej -

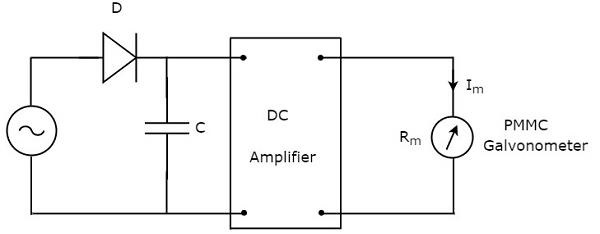
Powyższy obwód składa się z diody, kondensatora, wzmacniacza prądu stałego i galwanometru PMMC. Dioda obecna w powyższym obwodzie służy do prostowania. Tak więc dioda przekształca sygnał napięcia przemiennego w sygnał napięcia stałego. Kondensator ładuje się do wartości szczytowej tego sygnału napięcia stałego.

W trakcie positive half cycleprzy sygnale napięcia przemiennego, dioda przewodzi, a kondensator ładuje się do wartości szczytowej sygnału napięcia przemiennego. Gdy wartość sygnału napięcia przemiennego jest mniejsza od tej wartości, dioda będzie spolaryzowana odwrotnie.

W ten sposób kondensator będzie się rozładowywał przez rezystor wzmacniacza prądu stałego aż do następnego dodatniego półcyklu sygnału napięcia zmiennego. Gdy wartość sygnału napięcia zmiennego jest większa niż napięcie kondensatora, dioda przewodzi i proces zostanie powtórzony.

Wartości składowe dobieramy w taki sposób, aby kondensator szybko się ładował i powoli się rozładowywał. W rezultacie miernik zawsze reaguje na to napięcie kondensatora, tjpeak value of AC voltage.

Woltomierz AC odpowiadający True RMS

Jak sugeruje nazwa, prawdziwy odpowiadający woltomierz prądu przemiennego RMS reaguje na rzeczywiste wartości RMS sygnału napięcia prądu przemiennego. Ten woltomierz mierzy wartości skuteczne napięcia przemiennego. Plikcircuit diagram woltomierza AC odpowiadającego prawdziwej wartości skutecznej RMS pokazano na poniższym rysunku.

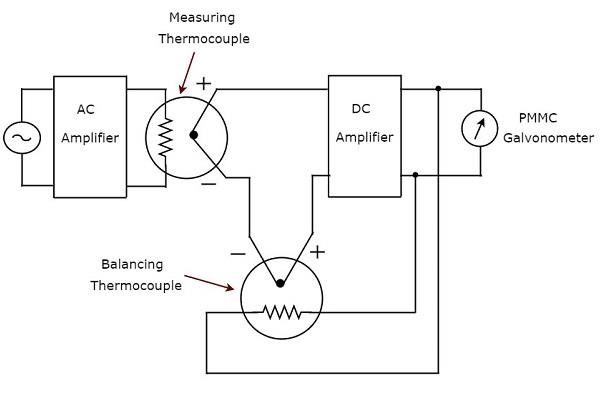
Powyższy obwód składa się ze wzmacniacza prądu przemiennego, dwóch termopar, wzmacniacza prądu stałego i galwanometru PMMC. Wzmacniacz AC wzmacnia sygnał napięcia AC. Dwie termopary używane w powyższym obwodzie to termopara pomiarowa i termopara równoważąca.Measuring thermocouple wytwarza napięcie wyjściowe, które jest proporcjonalne do wartości skutecznej sygnału napięcia przemiennego.

Każda termopara przekształca kwadrat wielkości wejściowej w normalną wielkość. Oznacza to, że istnieje nieliniowa zależność między wyjściem a wejściem termopary. Wpływ nieliniowego zachowania termopary można pominąć, stosując inną termoparę w obwodzie sprzężenia zwrotnego. Termopara, która jest używana w tym celu w powyższym obwodzie, jest znana jakobalancing thermocouple.

Dwie termopary, mianowicie termopara pomiarowa i termopara równoważąca, tworzą razem pannę młodą na wejściu wzmacniacza prądu stałego. W rezultacie miernik zawsze reaguje natrue RMS value sygnału napięcia zmiennego.

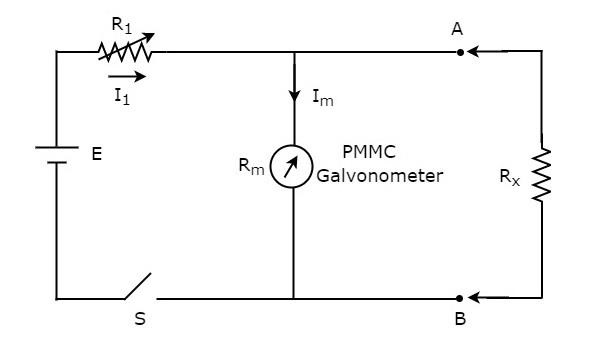
Prąd to szybkość przepływu ładunku elektrycznego. Jeśli ten ładunek elektryczny płynie tylko w jednym kierunku, to prąd wypadkowy nazywany jest prądem stałym (DC). Przyrząd, który służy do pomiaru prądu stałego o nazwieDC ammeter.

Jeśli umieścimy rezystor równolegle z galwanometrem z ruchomą cewką z magnesem trwałym (PMMC), to cała kombinacja będzie działać jako amperomierz prądu stałego. Opór równoległy, który jest używany w amperomierzu prądu stałego, jest również nazywany rezystancją bocznikową lub po prostushunt. Wartość tej rezystancji należy uznać za małą, aby zmierzyć prąd stały o dużej wartości.

Plik circuit diagram amperomierza prądu stałego pokazano na poniższym rysunku.

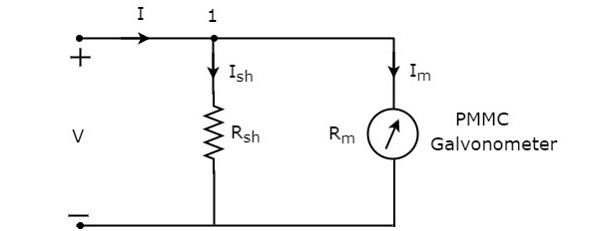
Musimy to umieścić DC ammeterszeregowo z odgałęzieniem obwodu elektrycznego, w którym ma być mierzony prąd stały. Napięcie na elementach połączonych równolegle jest takie samo. Więc napięcie na rezystorze bocznikowym,$R_{sh}$ i napięcie na rezystancji galwanometru, $R_{m}$ jest tak samo, ponieważ te dwa elementy są połączone równolegle w powyższym obwodzie. Mathematically, można go zapisać jako

$$I_{sh}R_{sh}=I_{m}R_{m}$$

$\Rightarrow R_{sh}=\frac{I_{m}R_{m}}{I_{sh}}$ (Równanie 1)

Plik KCL equation w węźle 1 jest

$$-I+I_{sh}+I_{m}=0$$

$$\Rightarrow I_{sh}=I-I_{m}$$

Substitute wartość $I_{sh}$ w równaniu 1.

$R_{sh}=\frac{I_{m}R_{m}}{I-I_{m}}$(Równanie 2)

Brać, $I_{m}$ jako wspólny w mianowniku, który znajduje się po prawej stronie równania 2

$$R_{sh}=\frac{I_{m}R_{m}}{I_{m}(\frac{1}{I_{m}}-1)}$$

$\Rightarrow R_{sh}=\frac{R_{m}}{\frac{I}{I_{m}}-1}$(Równanie 3)

Gdzie,

$R_{sh}$ jest opór bocznikowy

$R_{m}$ jest oporem wewnętrznym galwanometru

$I$ to całkowity prąd stały, który ma zostać zmierzony

$I_{m}$ jest prądem odchylającym w pełnej skali

Stosunek całkowitego prądu stałego, który ma być zmierzony, $I$ i pełnego odchylenia prądu galwanometru, $I_{m}$ jest znany jako multiplying factor, m. Matematycznie można to przedstawić jako

$m=\frac{I}{I_{m}}$(Równanie 4)

$R_{sh}=\frac{R_{m}}{m-1}$(Równanie 5)

Możemy znaleźć value of shunt resistance używając Równania 2 lub Równania 5 w oparciu o dostępne dane.

Wielozakresowy amperomierz prądu stałego

W poprzednim rozdziale omówiliśmy amperomierz prądu stałego, który uzyskuje się poprzez umieszczenie rezystora równolegle z galwanometrem PMMC. Ten amperomierz prądu stałego może być używany do pomiaruparticular range prądów stałych.

Jeśli chcemy użyć amperomierza prądu stałego do pomiaru prądów stałych o multiple ranges, wtedy musimy użyć wielu równoległych rezystorów zamiast pojedynczego rezystora, a cała ta kombinacja rezystorów jest równoległa do galwanometru PMMC. Plikcircuit diagram amperomierza wielozakresowego prądu stałego pokazano na poniższym rysunku.

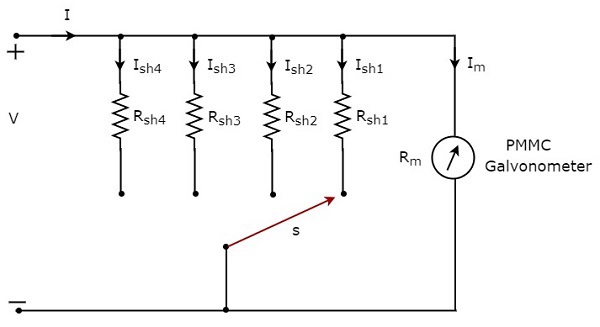
Ten wielozakresowy amperomierz prądu stałego należy umieścić szeregowo z odgałęzieniem obwodu elektrycznego, w którym ma być mierzony prąd stały o wymaganym zakresie. Żądany zakres prądów jest wybierany poprzez podłączenie przełącznika s do odpowiedniego rezystora bocznikowego.

Pozwolić, $m_{1}, m_{2}, m_{3}$ i $m_{4}$ są multiplying factors amperomierza prądu stałego, gdy uważamy, że całkowity prąd stały jest mierzony jako, $I_{1}, I_{2}, I_{3}$ i $I_{4}$odpowiednio. Poniżej znajdują się wzory odpowiadające każdemu mnożnikowi.

$$m_{1}=\frac{I_{1}}{I_{m}}$$

$$m_{2}=\frac{I_{2}}{I_{m}}$$

$$m_{3}=\frac{I_{3}}{I_{m}}$$

$$m_{4}=\frac{I_{4}}{I_{m}}$$

W powyższym obwodzie są cztery shunt resistors, $R_{sh1}, R_{sh2}, R_{sh2}$ i $R_{sh4}$. Poniżej znajdują się wzory odpowiadające tym czterem rezystorom.

$$R_{sh1}=\frac{R_{m}}{m_{1}-1}$$

$$R_{sh2}=\frac{R_{m}}{m_{2}-1}$$

$$R_{sh3}=\frac{R_{m}}{m_{3}-1}$$

$$R_{sh4}=\frac{R_{m}}{m_{4}-1}$$

Powyższe wzory pomogą nam znaleźć wartości rezystancji każdego rezystora bocznikowego.

Prąd to szybkość przepływu ładunku elektrycznego. Jeśli kierunek tego ładunku elektrycznego zmienia się regularnie, wówczas wywoływany jest prąd wypadkowyAlternating Current (AC).

Przyrząd, który służy do pomiaru prądu przemiennego przepływającego przez dowolną gałąź obwodu elektrycznego, nazywa się AC ammeter.

Example - Amperomierz typu AC z termoparą.

Omówmy teraz amperomierz typu AC z termoparą.

Amperomierz z termoparą typu AC

Jeśli przed galwanometrem PMMC podłączona jest termopara, cała ta kombinacja nazywana jest amperomierzem termopary typu AC. Plikblock diagram amperomierza typu AC z termoparą pokazano na poniższym rysunku.

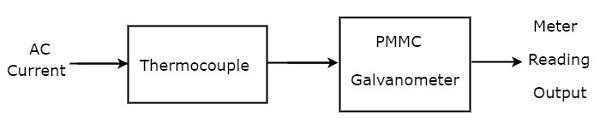
Powyższy schemat blokowy składa się głównie z dwóch bloków: termopary i galwanometru PMMC. Otrzymamy odpowiedni schemat obwodu, po prostu zastępując każdy blok odpowiednimi komponentami z powyższego schematu blokowego. Tak więccircuit diagram amperomierza AC typu termopary będzie wyglądać tak, jak pokazano na poniższym rysunku.

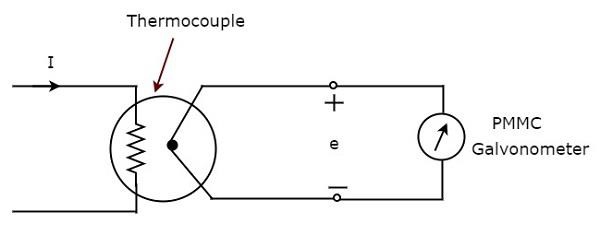
Termopara generuje EMF, $e$, ilekroć prąd przemienny przepływa przez element grzejny. Ten EMF,$e$jest wprost proporcjonalna do wartości skutecznej prądu I przepływającego przez element grzejny. Musimy więc skalibrować skalę instrumentu PMMC do odczyturms values of current.

Tak więc w tym rozdziale skompletowaliśmy wszystkie podstawowe przyrządy pomiarowe, takie jak woltomierze DC, woltomierze AC, amperomierze DC i amperomierze AC. W następnym rozdziale omówimy mierniki lub przyrządy pomiarowe, które mierzą wartość rezystancji.

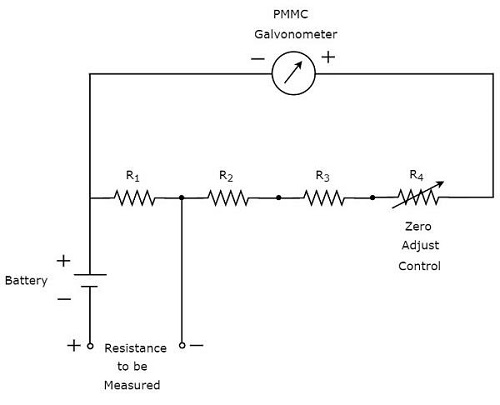
Przyrząd, który służy do pomiaru wartości rezystancji między dowolnymi dwoma punktami w obwodzie elektrycznym, nazywa się ohmmeter. Można go również użyć do znalezienia wartości nieznanego rezystora. Jednostkami rezystancji są omy, a przyrządem pomiarowym jest metr. Zatem słowo „omomierz” uzyskuje się poprzez połączenie słów“ohm” i “meter”.

Rodzaje omomierzy

Poniżej znajdują się pliki two types omomierzy.

• Omomierz szeregowy
• Omomierz bocznikowy

Omówmy teraz kolejno te dwa typy omomierzy.

Omomierz szeregowy

Jeśli wartość rezystora jest nieznana i musi być zmierzona poprzez umieszczenie go szeregowo z omomierzem, wówczas omomierz ten nazywany jest omomierzem szeregowym. Plikcircuit diagram szeregowego omomierza pokazano na poniższym rysunku.

Część obwodu, która jest lewa strona zacisków A i B jest series ohmmeter. Możemy więc zmierzyć wartość nieznanej rezystancji, umieszczając ją po prawej stronie zacisków A i B.Teraz omówimycalibration scale szeregowego omomierza.

• Gdyby $R_{x}= 0 \:\Omega$, wtedy zaciski A i B zostaną zwarte ze sobą. Tak więc prąd miernika zostaje podzielony między rezystory,$R_{1}$ i $R_{2}$. Teraz zmień wartość rezystora,$R_{2}$ w taki sposób, aby przez rezystor przepływał cały prąd licznika, $R_{1}$tylko. W tym przypadku miernik pokazuje pełnescale deflection current. Stąd ten pełny prąd odchylania miernika można przedstawić jako$0 \:\Omega$.

• Gdyby $R_{x}= \infty \:\Omega$, wtedy zaciski A i B zostaną otwarte w obwodzie ze sobą. Więc żaden prąd nie przepływa przez rezystor,$R_{1}$. W tym przypadku miernik wskazuje zerowy prąd odchylenia. Stąd to zerowe odchylenie miernika można przedstawić jako$\infty \Omega$.

• W ten sposób, biorąc pod uwagę różne wartości $R_{x}$miernik pokazuje różne ugięcia. Zatem odpowiednio możemy przedstawić te ugięcia za pomocą odpowiedniej wartości oporu.

Omomierz seryjny składa się ze skali kalibracyjnej. Ma wskazania 0$\Omega$ i $\infty \:\Omega$odpowiednio na końcach prawej i lewej ręki skali. Do pomiaru przydatny jest omomierz szeregowyhigh values of resistances.

Omomierz bocznikowy

Jeśli wartość rezystora jest nieznana i należy ją zmierzyć poprzez umieszczenie go równolegle (bocznik) z omomierzem, wówczas omomierz ten nazywa się omomierzem bocznikowym. Plikcircuit diagram omomierza bocznikowego pokazano na poniższym rysunku.

Część obwodu, która jest lewa strona zacisków A i B jest shunt ohmmeter. Możemy więc zmierzyć wartość nieznanej rezystancji, umieszczając ją po prawej stronie zacisków A i B.

Porozmawiajmy teraz o calibration scaleomomierza bocznikowego. Zamknij przełącznik, S powyższego obwodu, gdy jest używany.

• Gdyby $R_{x}=0 \:\Omega$, wtedy zaciski A i B zostaną zwarte ze sobą. Z tego powodu cały prąd,$I_{1}$przepływa przez zaciski A i B. W tym przypadku przez galwanometr PMMC nie płynie prąd. Stądnull deflection galwanometru PMMC można przedstawić jako $0 \:\Omega$.

• Gdyby $R_{x}=\infty \:\Omega$, wtedy zaciski A i B zostaną otwarte w obwodzie ze sobą. Zatem żaden prąd nie przepływa przez zaciski A i B. W tym przypadku cały prąd,$I_{1}$przepływa przez galwanometr PMMC. W razie potrzeby zmień (wyreguluj) wartość rezystora,$R_{1}$aż galwanometr PMMC wskaże prąd odchylenia w pełnej skali. Stąd tofull scale deflection prąd galwanometru PMMC można przedstawić jako $\infty \:\Omega$

• W ten sposób, biorąc pod uwagę różne wartości $R_{x}$miernik pokazuje różne ugięcia. Zatem odpowiednio możemy przedstawić te ugięcia za pomocą odpowiednich wartości oporu.

Omomierz bocznikowy składa się ze skali kalibracyjnej. Ma wskazania$0 \:\Omega$ i $\infty \:\Omega$ odpowiednio na końcach lewej i prawej strony skali.

Do pomiaru przydatny jest bocznikowy omomierz low values of resistances. Tak więc, możemy użyć omomierza szeregowego lub bocznikowego w oparciu o wartości rezystancji, które mają być zmierzone, tj. Wysokie lub niskie.

W poprzednich rozdziałach omawialiśmy woltomierze, amperomierze i omomierze. Te przyrządy pomiarowe służą do pomiaru odpowiednio napięcia, prądu i rezystancji. To znaczy, że mamyseparate measuring instruments do pomiaru napięcia, prądu i rezystancji.

Załóżmy, że jeśli pojedynczy przyrząd pomiarowy może być użyty do pomiaru wielkości, takich jak napięcie, prąd i rezystancja pojedynczo, to mówi się, że jest multimeter. Ma nazwę multimetr, ponieważ może mierzyć wiele wielkości elektrycznych pojedynczo.

Pomiary za pomocą multimetru

Multimeterto przyrząd służący do pomiaru napięć DC i AC, prądów DC i AC oraz rezystancji w kilku zakresach. Jest również nazywany elektronicznym multimetrem lub omomierzem napięcia (VOM).

Pomiar napięcia stałego

Część circuit diagram multimetru, którego można użyć do pomiaru napięcia stałego, pokazano na poniższym rysunku.

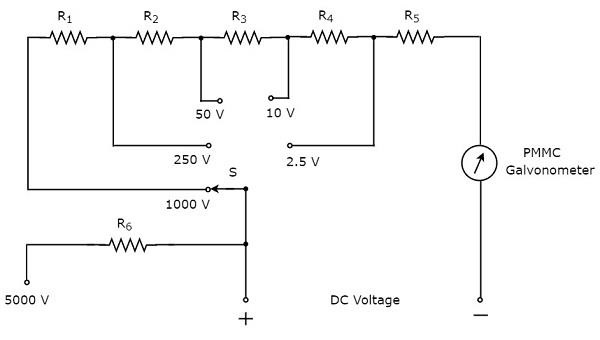
Powyższy obwód wygląda jak wielozakresowy woltomierz DC. Połączenie rezystora połączonego szeregowo z galwanometrem PMMC toDC voltmeter. Dzięki temu może służyć do pomiaru napięć stałych do określonej wartości.

Możemy zwiększyć zakres napięć DC, które można zmierzyć tym samym woltomierzem DC, zwiększając wartość rezystancji. równoważna wartość rezystancji wzrasta, gdy podłączymy rezystoryseries.

W powyższym obwodzie możemy mierzyć napięcia stałe do 2.5V za pomocą kombinacji rezystorów, $R_{5}$szeregowo z galwanometrem PMMC. Podłączając rezystor,$R_{4}$ szeregowo z poprzednim obwodem możemy mierzyć napięcia DC do 10V. W ten sposób możemy zwiększyć zakres napięć stałych, po prostu łącząc rezystor szeregowo z poprzednim (wcześniejszym) obwodem.

Możemy zmierzyć napięcie DC w dowolnych dwóch punktach obwodu elektrycznego, podłączając przełącznik S do żądanego zakresu napięcia.

Pomiar prądu stałego

Część circuit diagram multimetru, którego można użyć do pomiaru prądu stałego, pokazano na poniższym rysunku.

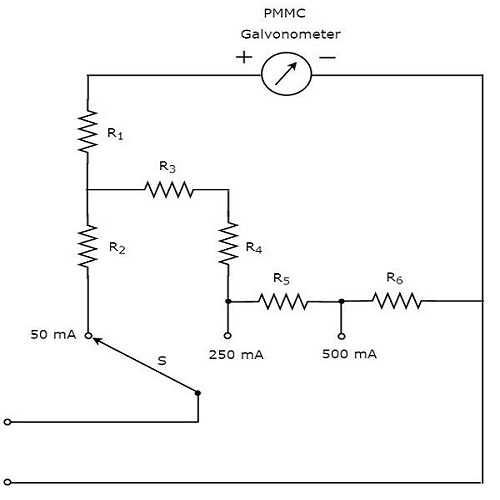
Powyższy obwód wygląda jak wielozakresowy amperomierz prądu stałego. połączenie rezystora równolegle z galwanometrem PMMC toDC ammeter. Dzięki temu może być używany do pomiaru prądów stałych do określonej wartości.

Możemy dostać different rangesprądów DC mierzonych tym samym amperomierzem DC poprzez umieszczenie rezystorów równolegle z poprzednim rezystorem. W powyższym obwodzie rezystor,$R_{1}$ jest połączony szeregowo z galwanometrem PMMC, aby zapobiec uszkodzeniu miernika z powodu dużego prądu.

Możemy zmierzyć prąd stały przepływający przez dowolne dwa punkty obwodu elektrycznego, podłączając przełącznik S do żądanego zakresu prądu

Pomiar napięcia AC

Część circuit diagram multimetru, którego można użyć do pomiaru napięcia AC, pokazano na poniższym rysunku.

Powyższy obwód wygląda jak a multi range AC voltmeter. Wiemy, że woltomierz AC otrzymamy po prostu ustawiając prostownik szeregowo (kaskadowo) z woltomierzem DC. Powyższy obwód powstał po prostu przez umieszczenie kombinacji diod i rezystora,$R_{6}$ pomiędzy rezystorem, $R_{5}$ i galwanometr PMMC.

Możemy zmierzyć napięcie AC w ​​dowolnych dwóch punktach obwodu elektrycznego, podłączając przełącznik S do żądanego zakresu napięcia.

Pomiar rezystancji

Część circuit diagram multimetru, którego można użyć do pomiaru rezystancji, pokazano na poniższym rysunku.

Przed wykonaniem jakichkolwiek pomiarów musimy wykonać następujące dwa zadania.

• Zewrzyj instrument
• Zmieniaj regulację zera, aż miernik pokaże prąd pełnej skali. Oznacza to, że miernik wskazuje zerową wartość rezystancji.

Teraz powyższy obwód zachowuje się jak omomierz bocznikowy i ma mnożenie skali 1, czyli 10 ⁰ . Możemy również rozważyć potęgi wyższego rzędu 10 jako mnożenia skali do pomiaru wysokich rezystancji.

Signal generator to urządzenie elektroniczne, które dostarcza standardowe sygnały testowe, takie jak sinusoida, fala prostokątna, fala trójkątna itp. Nazywa się go również oscylatorem, ponieważ wytwarza sygnały okresowe.

Wywoływany jest generator sygnału, który wytwarza okresowy sygnał o częstotliwości z zakresu częstotliwości audio (AF) AF signal generator. zakres częstotliwości audio wynosi od 20 Hz do 20 kHz.

Generator fal sinusoidalnych i prostokątnych AF

Generator sygnału AF, który generuje falę sinusoidalną lub prostokątną w zakresie częstotliwości audio w zależności od wymagań, nazywany jest generatorem fal sinusoidalnych i prostokątnych AF. Jegoblock diagrampokazano na poniższym rysunku.

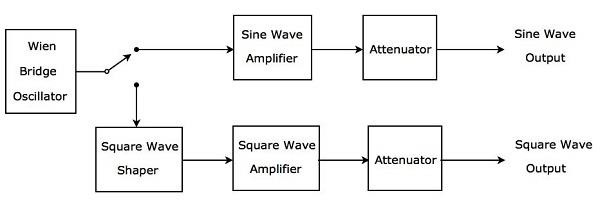
Powyższy schemat blokowy składa się głównie z plików two paths. To są ścieżki wyższe i ścieżki niższe. Ścieżka górna służy do wytwarzania fali sinusoidalnej AF, a ścieżka dolna do wytwarzania fali prostokątnej AF.

Wien bridge oscillatorwytworzy falę sinusoidalną w zakresie częstotliwości audio. W oparciu o wymagania możemy podłączyć wyjście oscylatora mostka Wien do górnej lub dolnej ścieżki za pomocą przełącznika.

Górna ścieżka składa się z bloków, takich jak wzmacniacz sinusoidalny i tłumik. Jeśli przełącznik jest używany do podłączenia wyjścia oscylatora mostka Wien do górnej ścieżki, wygeneruje pożądanyAF sine wave na wyjściu ścieżki górnej.

Dolna ścieżka składa się z następujących bloków: kształtowanie fali prostokątnej, wzmacniacz fali prostokątnej i tłumik. Moduł kształtowania fali prostokątnej przekształca falę sinusoidalną w falę prostokątną. Jeśli przełącznik jest używany do podłączenia wyjścia oscylatora mostka Wien do dolnej ścieżki, wówczas wygeneruje pożądanyAF square wavena wyjściu dolnej ścieżki. W ten sposób schemat blokowy, który rozważaliśmy, może być użyty do wytworzenia albo fali sinusoidalnej AF, albo fali prostokątnej AF w oparciu o wymagania.

Generator funkcyjny

Generator funkcji to generator sygnału, który generuje trzy lub więcej okresowych fal. Rozważ następująceblock diagram generatora funkcji, który będzie wytwarzał okresowe fale, takie jak fala trójkątna, prostokątna i sinusoidalna.

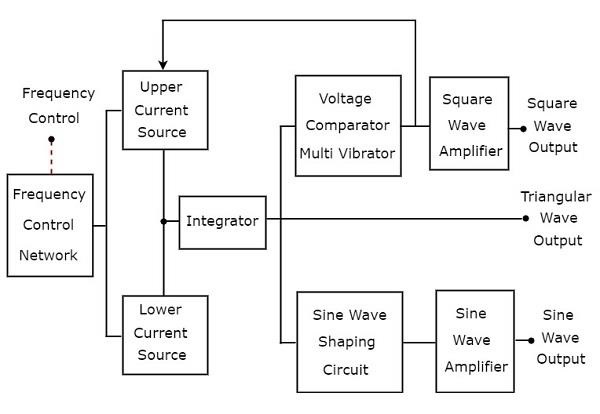
Istnieją dwa current sources, czyli górne źródło prądu i dolne źródło prądu na powyższym schemacie blokowym. Te dwa źródła prądu są regulowane przez napięcie o regulowanej częstotliwości.

Fala trójkątna

Integratorobecny na powyższym schemacie blokowym, wielokrotnie pobiera stały prąd naprzemiennie z górnych i dolnych źródeł prądu przez równy czas. Tak więc integrator będzie wytwarzał dwa typy danych wyjściowych w tym samym czasie wielokrotnie -

• Napięcie wyjściowe integratora increases linearly w odniesieniu do czasu za okres, w którym integrator pobiera prąd z górnego źródła prądu.

• Napięcie wyjściowe integratora decreases linearly w odniesieniu do czasu za okres, w którym integrator pobiera prąd z niższego źródła prądu.

W ten sposób integrator obecny na powyższym schemacie blokowym utworzy plik triangular wave.

Fala prostokątna i sinusoidalna

Wyjście integratora, tj. Fala trójkątna, jest stosowane jako wejście do dwóch innych bloków, jak pokazano na powyższym schemacie blokowym, w celu uzyskania odpowiednio fali prostokątnej i fali sinusoidalnej. Porozmawiajmy o tych dwóch jeden po drugim.

Kwadratowa fala

Fala trójkątna ma nachylenie dodatnie i ujemne naprzemiennie przez taki sam okres czasu. Tak więcvoltage comparator multi vibrator obecny na powyższym schemacie blokowym będzie wielokrotnie wytwarzał następujące dwa typy danych wyjściowych przez taki sam okres czasu.

• Jeden rodzaj stałej (higher) voltage na wyjściu komparatora napięcia multi-wibratora za okres, w którym komparator napięcia multi-wibrator uzyskuje dodatnie nachylenie fali trójkątnej.

• Inny rodzaj stałej (lower) voltage na wyjściu komparatora napięcia multi wibrator za okres, w którym komparator napięcia multi wibrator uzyskuje ujemne nachylenie fali trójkątnej.

Wielowibrator komparatora napięcia przedstawiony na powyższym schemacie blokowym da square wave. Jeżeli amplituda fali prostokątnej, która jest wytwarzana na wyjściu wielowibratora komparatora napięcia, jest niewystarczająca, można ją wzmocnić do wymaganej wartości za pomocą wzmacniacza fali prostokątnej.

Sinusoida

Plik sine wave shaping circuitwygeneruje falę sinusoidalną z trójkątnej fali wejściowej. Zasadniczo ten obwód składa się z sieci rezystancyjnej diody. Jeżeli amplituda fali sinusoidalnej wytwarzanej na wyjściu obwodu kształtującego falę sinusoidalną jest niewystarczająca, można ją wzmocnić do wymaganej wartości za pomocą wzmacniacza sinusoidalnego.

Elektroniczny instrument używany do analizy fal to tzw wave analyzer. Jest również nazywany analizatorem sygnału, ponieważ terminy sygnał i fala mogą być często używane zamiennie.

Możemy reprezentować periodic signal jako suma następujących dwóch wyrazów.

• Składnik DC
• Szeregi harmonicznych sinusoidalnych

Zatem analiza sygnału okresowego jest analizą składowych harmonicznych w nim występujących.

Podstawowy analizator fal

Podstawowy analizator fal składa się głównie z trzech bloków - detektora pierwotnego, prostownika pełnookresowego i galwanometru PMMC. Plikblock diagram podstawowego analizatora przebiegu pokazano na poniższym rysunku -

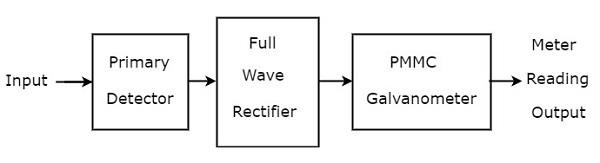
Plik function każdego bloku obecnego w podstawowym analizatorze fal opisano poniżej.

• Primary Detector- Składa się z obwodu LC. Możemy dostosować wartości cewki indukcyjnej, L i kondensatora C w taki sposób, aby umożliwić pomiar tylko pożądanej składowej harmonicznej, która ma być zmierzona.

• Full Wave Rectifier - Konwertuje wejście AC na wyjście DC.

• PMMC Galvanometer - Pokazuje wartość szczytową sygnału, jaki jest uzyskiwany na wyjściu prostownika pełnookresowego.

Otrzymamy odpowiedni schemat obwodu, po prostu zastępując każdy blok odpowiednimi komponentami z powyższego schematu blokowego podstawowego analizatora fal. Tak więccircuit diagram podstawowego analizatora fal będzie wyglądać tak, jak pokazano na poniższym rysunku -

Ten podstawowy analizator fal może być używany do analizy każdej składowej harmonicznej częstotliwości sygnału okresowego.

Rodzaje analizatorów fal

Analizatory fal można podzielić na następujące two types.

• Analizator fal selektywnych częstotliwości
• Analizator fal superheterodynowych

Omówmy teraz kolejno te dwa analizatory fal.

Analizator fal selektywnych częstotliwości

Analizator fal służący do analizy sygnałów z zakresu AF nazywany jest analizatorem fal selektywnych częstotliwościowo. Plikblock diagram Poniższy rysunek przedstawia analizator częstotliwości selektywnej.

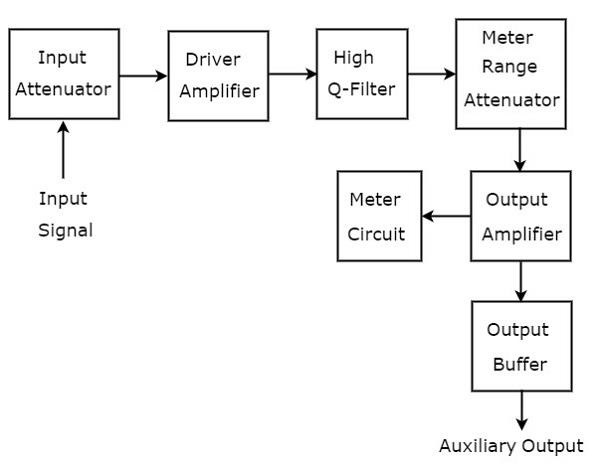
Analizator fali selektywnej częstotliwości składa się z zestawu bloków. Plikfunction każdego bloku wymieniono poniżej.

• Input Attenuator- Sygnał AF, który ma być analizowany, podawany jest na tłumik wejściowy. Jeśli amplituda sygnału jest zbyt duża, można ją stłumić za pomocą tłumika wejściowego.

• Driver Amplifier - Wzmacnia odbierany sygnał, gdy jest to konieczne.

• High Q-filter- Służy do wybierania żądanej częstotliwości i odrzucania niepożądanych częstotliwości. Składa się z dwóch sekcji RC i dwóch wzmacniaczy filtrów, które są połączone kaskadowo. Możemy zmieniać wartości pojemności dla zmiany zakresu częstotliwości w potęgach 10. Podobnie, możemy zmieniać wartości rezystancji, aby zmienić częstotliwość w wybranym zakresie.

• Meter Range Attenuator - Pobiera wybrany sygnał AF jako wejście i wytwarza stłumiony sygnał wyjściowy, gdy jest to wymagane.

• Output Amplifier - W razie potrzeby wzmacnia wybrany sygnał AF.

• Output Buffer - Służy do dostarczania wybranego sygnału AF do urządzeń wyjściowych.

• Meter Circuit- Wyświetla odczyt wybranego sygnału AF. Możemy wybrać odczyt miernika w zakresie woltów lub w decybelach.

Analizator fal superheterodynowych

Analizator fal, używany do analizy sygnałów z zakresu RF, nazywany jest analizatorem fal superheterodynowych. Poniższy rysunek przedstawiablock diagram analizatora fal superheterodynowych.

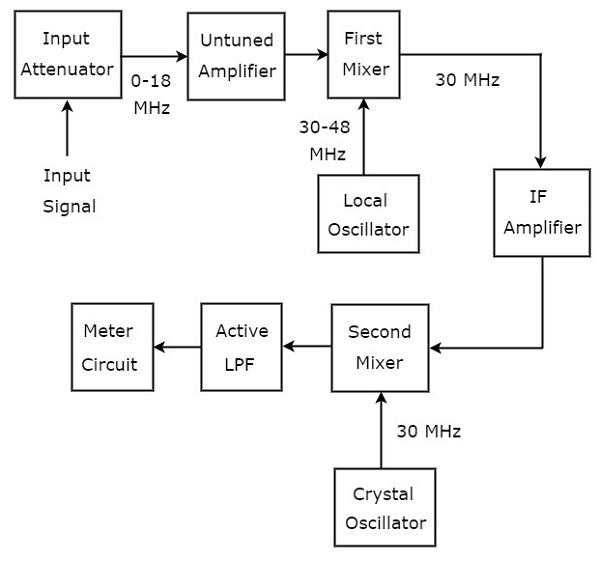
Plik working analizatora fal superheterodynowych omówiono poniżej.

• Analizowany sygnał RF podawany jest do tłumika wejściowego. Jeśli amplituda sygnału jest zbyt duża, można ją stłumić za pomocąinput attenuator.

• Untuned amplifier wzmacnia sygnał RF w razie potrzeby i jest podawany do pierwszego miksera.

• Zakresy częstotliwości sygnału RF i wyjścia lokalnego oscylatora to odpowiednio 0-18 MHz i 30-48 MHz. Więc,first mixergeneruje sygnał wyjściowy o częstotliwości 30 MHz. Jest to różnica częstotliwości dwóch sygnałów, które są do niego stosowane.

• IF amplifierwzmacnia sygnał częstotliwości pośredniej (IF), tj. sygnał wyjściowy pierwszego miksera. Wzmocniony sygnał IF jest podawany do drugiego miksera.

• Częstotliwości wzmocnionego sygnału IF i wyjście oscylatora Crystal są takie same i równe 30 MHz. Tak więcsecond mixerwytwarza sygnał wyjściowy o częstotliwości 0 Hz. Jest to różnica częstotliwości dwóch sygnałów, które są do niego stosowane.

• Częstotliwość odcięcia Active Low Pass Filter (LPF)jest wybrana jako 1500 Hz. Stąd ten filtr dopuszcza sygnał wyjściowy drugiego miksera.

• Meter Circuitwyświetla odczyt sygnału RF. Możemy wybrać odczyt miernika w zakresie woltów lub w decybelach.

Możemy więc wybrać konkretny analizator fal na podstawie zakresu częstotliwości sygnału, który ma być analizowany.

Elektroniczny instrument używany do analizy fal w dziedzinie częstotliwości nazywa się spectrum analyzer. Zasadniczo wyświetla rozkład energii sygnału na ekranie CRT. Tutaj oś X przedstawia częstotliwość, a oś Y reprezentuje amplitudę.

Rodzaje analizatorów widma

Możemy podzielić analizatory widma na następujące two types.

• Analizator widma banku filtrów
• Analizator widma superheterodynowego

Omówmy teraz kolejno te dwa analizatory widma.

Analizator widma banku filtrów

Analizator widma, używany do analizy sygnałów z zakresu AF, nazywany jest analizatorem widma banku filtrów lub real time spectrum analyzer ponieważ pokazuje (wyświetla) wszelkie zmiany we wszystkich częstotliwościach wejściowych.

Poniższy rysunek przedstawia block diagram analizatora widma banku filtrów.

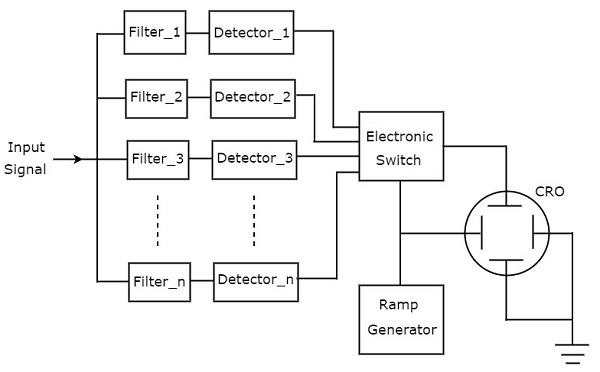
Plik working analizatora widma banku filtrów jest wymieniony poniżej.

• Posiada zestaw filtrów pasmowo-przepustowych, a każdy z nich jest zaprojektowany tak, aby zezwalał na określone pasmo częstotliwości. Sygnał wyjściowy każdego filtra pasmowoprzepustowego jest przekazywany do odpowiedniego detektora.

• Wszystkie wyjścia czujki są podłączone do przełącznika elektronicznego. Przełącznik ten pozwala na sekwencyjne wyjścia detektora z płytą odchylania pionowego CRO. Tak więc CRO wyświetla częstotliwośćspectrum of AF signal na ekranie CRT.

Analizator widma superheterodynowego

Nazywa się analizator widma, używany do analizy sygnałów o zakresie RF superheterodyne spectrum analyzer. Jegoblock diagram pokazano na poniższym rysunku.

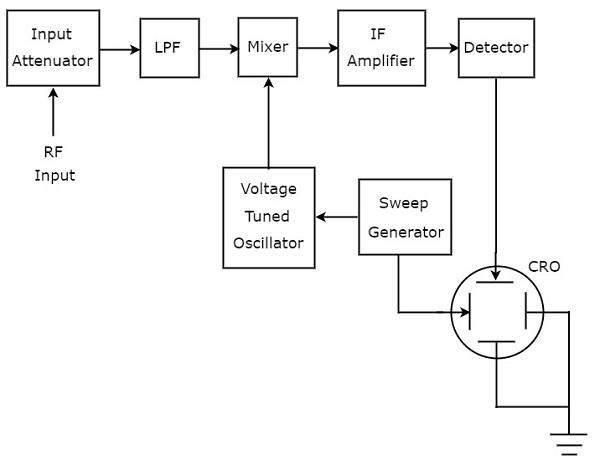
Plik working analizatora widma superheterodynowego wymieniono poniżej.

• Analizowany sygnał RF doprowadzany jest do tłumika wejściowego. Jeśli amplituda sygnału jest zbyt duża, można ją stłumić za pomocąinput attenuator.

• Low Pass Filter (LPF) dopuszcza tylko składowe częstotliwości, które są mniejsze niż częstotliwość odcięcia.

• Mixerpobiera dane wejściowe z filtra dolnoprzepustowego i oscylatora dostrojonego pod napięciem. Generuje wyjście, które jest różnicą częstotliwości dwóch sygnałów, które są do niego przyłożone.

• IF amplifierwzmacnia sygnał częstotliwości pośredniej (IF), tj. wyjście miksera. Wzmocniony sygnał IF jest doprowadzany do detektora.

Sygnał wyjściowy detektora jest podawany na płytkę odchylania pionowego CRO. Tak więc CRO wyświetla częstotliwośćspectrum of RF signal na ekranie CRT.

Możemy więc wybrać konkretny analizator widma na podstawie zakresu częstotliwości sygnału, który ma być analizowany.

Oscilloscopeto urządzenie elektroniczne, które wyświetla przebieg napięcia. Spośród oscyloskopów podstawowym oscyloskopem jest oscyloskop katodowy (CRO), który wyświetla zmienny w czasie sygnał lub przebieg.

W tym rozdziale omówimy schemat blokowy CRO i pomiary niektórych parametrów za pomocą CRO.

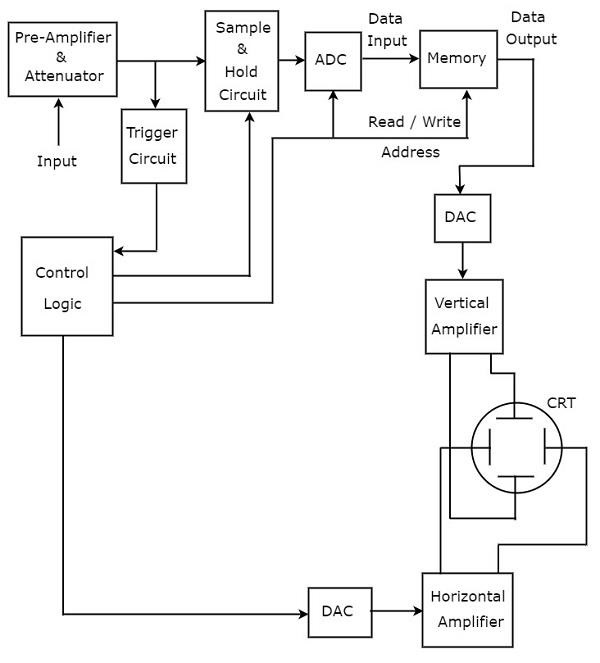
Schemat blokowy CRO

Oscyloskop katodowy (CRO) składa się z zestawu bloków. Są to: wzmacniacz pionowy, linia opóźniająca, obwód wyzwalania, generator podstawy czasu, wzmacniacz poziomy, kineskop (CRT) i zasilacz. Plikblock diagram CRO pokazano na poniższym rysunku.

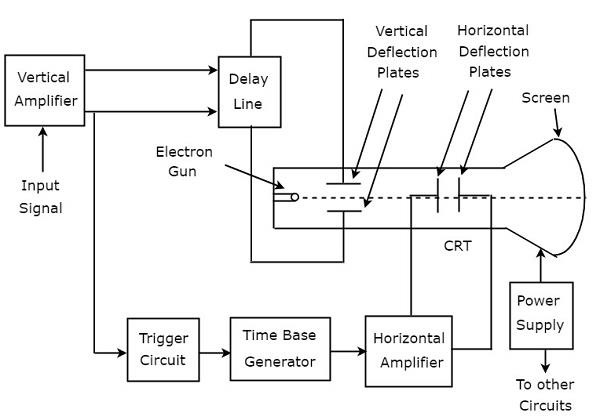
Plik function każdego bloku CRO jest wymienione poniżej.

• Vertical Amplifier - Wzmacnia sygnał wejściowy, który ma być wyświetlany na ekranie CRT.

• Delay Line- Zapewnia pewne opóźnienie sygnału, które jest uzyskiwane na wyjściu wzmacniacza pionowego. Ten opóźniony sygnał jest następnie podawany na płyty odchylania pionowego CRT.

• Trigger Circuit - Wytwarza sygnał wyzwalający, aby zsynchronizować zarówno poziome, jak i pionowe odchylenia wiązki elektronów.

• Time base Generator - Wytwarza sygnał piłokształtny, który jest przydatny przy odchylaniu wiązki elektronów w poziomie.

• Horizontal Amplifier - Wzmacnia sygnał piłokształtny, a następnie łączy go z poziomymi płytkami odchylającymi CRT.

• Power supply- Wytwarza zarówno wysokie, jak i niskie napięcia. Ujemne wysokie napięcie i dodatnie niskie napięcie są podawane odpowiednio do CRT i innych obwodów.

• Cathode Ray Tube (CRT)- Jest to główny ważny blok CRO i składa się głównie z czterech części. Są to działa elektronowe, pionowe płytki odchylające, poziome płytki odchylające oraz ekran fluorescencyjny.

Wiązka elektronów wytwarzana przez wyrzutnię elektronową jest odchylana w kierunku pionowym i poziomym odpowiednio przez parę pionowych płyt odchylających i parę poziomych płyt odchylających. Wreszcie odchylona wiązka pojawi się jako plamka na ekranie fluorescencyjnym.

W ten sposób CRO wyświetli zastosowany sygnał wejściowy na ekranie CRT. Zatem możemy analizować sygnały w dziedzinie czasu za pomocą CRO

Pomiary za pomocą CRO

Możemy wykonać następujące pomiary za pomocą CRO.

• Pomiar amplitudy
• Pomiar okresu czasu
• Pomiar częstotliwości

Omówmy teraz kolejno te pomiary.

Pomiar amplitudy

CRO wyświetla na ekranie sygnał napięcia w funkcji czasu. Plikamplitude tego sygnału napięciowego jest stały, ale możemy zmieniać liczbę działek pokrywających sygnał napięcia w kierunku pionowym, zmieniając volt/divisionpokrętło na panelu CRO. Dlatego otrzymamy plikamplitude sygnału, który jest obecny na ekranie CRO za pomocą następującego wzoru.

$$A=j\times n_{v}$$

Gdzie,

$A$ jest amplitudą

$j$ jest wartością wolta / działki

$n_{v}$ jest liczbą działek pokrywających sygnał w kierunku pionowym.

Pomiar okresu czasu

CRO wyświetla na ekranie sygnał napięcia w funkcji czasu. PlikTime period tego okresowego sygnału napięciowego jest stała, ale możemy zmieniać liczbę działek, które obejmują jeden pełny cykl sygnału napięciowego w kierunku poziomym, zmieniając time/division pokrętło na panelu CRO.

Dlatego otrzymamy plik Time period sygnału, który jest obecny na ekranie CRO za pomocą następującego wzoru.

$$T=k\times n_{h}$$

Gdzie,

$T$ to okres czasu

$j$ to wartość czasu / podziału

$n_{v}$ jest liczbą działek, które obejmują jeden pełny cykl okresowego sygnału w kierunku poziomym.

Pomiar częstotliwości

Częstotliwość f sygnału okresowego jest odwrotnością okresu czasu, T. Mathematically, można go przedstawić jako

$$f=\frac{1}{T}$$

Zatem możemy znaleźć częstotliwość f okresowego sygnału, wykonując te dwa kroki.

• Step1 - Znajdź Time period okresowego sygnału

• Step2 - Weź reciprocal Okresu sygnału okresowego, który jest uzyskiwany w kroku 1

O oscyloskopach do zastosowań specjalnych omówimy w następnym rozdziale.

W poprzednim rozdziale omówiliśmy oscyloskop katodowy (CRO), który jest podstawowym oscyloskopem. Oscyloskopy specjalnego przeznaczenia otrzymamy, dołączając kilka dodatkowych bloków do podstawowego oscyloskopu w oparciu o wymagania.

Poniżej znajdują się pliki special purpose oscilloscopes.

• Oscyloskop dwuwiązkowy
• Oscyloskop z podwójnym śladem
• Cyfrowy oscyloskop z pamięcią

Omówmy teraz kolejno te oscyloskopy do zastosowań specjalnych.

Oscyloskop dwuwiązkowy

Oscyloskop, który wyświetla dwa przebiegi napięcia, nazywany jest oscyloskopem dwuwiązkowym. Jegoblock diagram pokazano na poniższym rysunku.

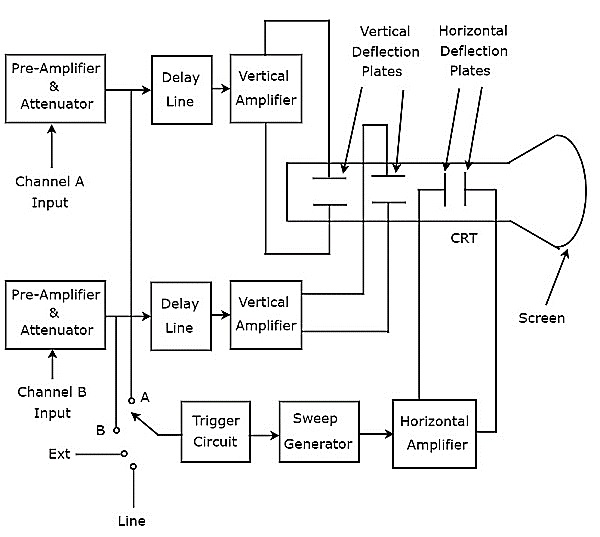
Jak pokazano na powyższym rysunku, CRT oscyloskopu dwuwiązkowego składa się z dwóch zestawów pionowych płytek odchylających i jednego zestawu poziomych płytek odchylających.

Połączenie następujących bloków razem nazywa się a channel.

• Przedwzmacniacz i tłumik
• Linia opóźniająca
• Wzmacniacz pionowy
• Zestaw płyt ugięcia pionowego

Oscyloskop dwuwiązkowy posiada dwa kanały. Zatem możemy zastosować dwa sygnały, a mianowicie A i B, jako wejście odpowiednio kanału A i kanału B. Możemy wybrać dowolny z tych czterech sygnałów jakotrigger inputdo obwodu wyzwalania za pomocą przełącznika. Są to sygnały wejściowe A i B, sygnał zewnętrzny (Ext) i wejście liniowe.

Ten oscyloskop będzie wytwarzał dwie wiązki odchylane w pionie, ponieważ istnieją dwie pary pionowych płyt odchylających. W tym oscyloskopie bloki przydatne do odchylania wiązki w kierunku poziomym są wspólne dla obu sygnałów wejściowych. Wreszcie ten oscyloskop wygeneruje pliktwo input signals jednocześnie na ekranie CRT.

Oscyloskop z podwójnym śladem

Oscyloskop, który generuje dwa ślady na ekranie, nazywa się oscyloskopem Dual Trace. Jegoblock diagram pokazano na poniższym rysunku.

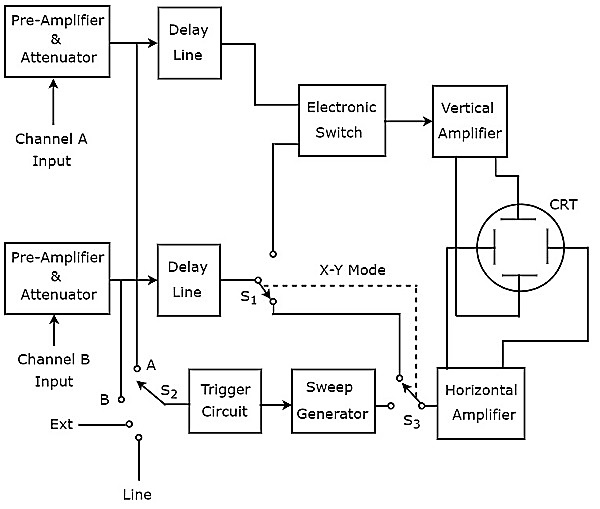
Jak pokazano na powyższym rysunku, CRT oscyloskopu Dual Trace składa się z zestawu pionowych płytek odchylających i innego zestawu poziomych płytek odchylających. Kanał składa się z czterech bloków, tj. przedwzmacniacza i tłumika, linii opóźniającej, wzmacniacza pionowego i płytek odchylania pionowego.

Na powyższym schemacie blokowym pierwsze dwa bloki są oddzielnie obecne w obu kanałach. Ostatnie dwa bloki są wspólne dla obu kanałów. Stąd za pomocąelectronic switch możemy podłączyć wyjście liniowe opóźnienia określonego kanału do wzmacniacza pionowego.

Możemy wybrać dowolny z tych czterech sygnałów jako wejście wyzwalające do trigger circuitza pomocą przełącznika. Są to sygnały wejściowe A i B, sygnał zewnętrzny (Ext) i wejście liniowe.

Ten oscyloskop wykorzystuje tę samą wiązkę elektronów do odchylania sygnałów wejściowych A i B w kierunku pionowym za pomocą przełącznika elektronicznego i wytwarza two traces. bloki odchylające wiązkę w poziomie są wspólne dla obu sygnałów wejściowych.

Cyfrowy oscyloskop z pamięcią

Oscyloskop, który przechowuje cyfrowo przebieg, jest znany jako oscyloskop cyfrowy. Plikblock diagram (cyfrowego) oscyloskopu z pamięcią poniżej -

Dodatkowe bloki wymagane do cyfrowego przechowywania danych są dodawane do podstawowego oscyloskopu, aby przekształcić go w oscyloskop cyfrowy z pamięcią. Bloki wymagane dostoring of digital dataznajdują się pomiędzy przedwzmacniaczem i tłumikiem a wzmacniaczem pionowym w oscyloskopie cyfrowym. Są to obwód próbkowania i wstrzymania, przetwornik analogowo-cyfrowy (ADC), pamięć i przetwornik cyfrowo-analogowy.

Control logicsteruje trzema pierwszymi blokami, wysyłając różne sygnały sterujące. Bloki takie jak logika sterująca i przetwornik cyfrowo-analogowy znajdują się między obwodem wyzwalania a wzmacniaczem poziomym w oscyloskopie cyfrowym z pamięcią.

Cyfrowy oscyloskop z pamięcią masową stores the datacyfrowo, zanim wyświetli przebieg na ekranie. Natomiast podstawowy oscyloskop nie ma tej funkcji.

Lissajous figureto wzór, który jest wyświetlany na ekranie, gdy sygnały sinusoidalne są stosowane zarówno do płyt odchylania poziomego, jak i pionowego CRO. Wzorce te będą się różnić w zależności od amplitud, częstotliwości i różnic fazowych sygnałów sinusoidalnych, które są stosowane zarówno na płytach odchylania poziomego, jak i pionowego CRO.

Poniższy rysunek przedstawia plik example postaci Lissajous.

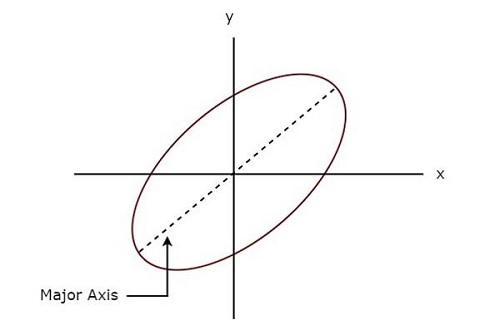
Powyższa figura Lissajous jest w elliptical shape a jego główna oś ma pewien kąt nachylenia z dodatnią osią X.

Pomiary z wykorzystaniem liczb Lissajous

Możemy wykonać następujące czynności two measurements z postaci Lissajous.

• Częstotliwość sygnału sinusoidalnego
• Różnica faz między dwoma sygnałami sinusoidalnymi

Omówmy teraz kolejno te dwa pomiary.

Pomiar częstotliwości

Figura Lissajous zostanie wyświetlona na ekranie, gdy sygnały sinusoidalne zostaną przyłożone do obu płyt odchylania poziomego i pionowego CRO. Dlatego zastosuj sygnał sinusoidalny, który ma standardknown frequencydo odchylaczy poziomych CRO. Podobnie zastosuj sygnał sinusoidalny, któregofrequency jest unknown do pionowych płyt odchylających CRO

Pozwolić, $f_{H}$ i $f_{V}$są częstotliwościami sygnałów sinusoidalnych, które są przykładane odpowiednio do płyt odchylania poziomego i pionowego CRO. Związek pomiędzy$f_{H}$ i $f_{V}$ może być mathematically przedstawione poniżej.

$$\frac{f_{V}}{f_{H}}=\frac{n_{H}}{n_{V}}$$

Z powyższej zależności otrzymamy częstotliwość sygnału sinusoidalnego, który jest przykładany do płyt odchylania pionowego CRO jako

$f_{V}=\left ( \frac{n_{H}}{n_{V}} \right )f_{H}$(Równanie 1)

Gdzie,

$n_{H}$ jest liczbą poziomych stycznych

$n_{V}$ jest liczbą stycznych pionowych

Możemy znaleźć wartości $n_{H}$ i $n_{V}$z figury Lissajous. Tak więc, zastępując wartości$n_{H}$, $n_{V}$ i $f_{H}$ w równaniu 1 otrzymamy wartość $f_{V}$, czyli frequency of sinusoidal signal który jest stosowany do pionowych płyt odchylających CRO.

Pomiar różnicy faz

Figura Lissajous jest wyświetlana na ekranie, gdy sygnały sinusoidalne są przyłożone do obu płyt odchylających poziomych i pionowych CRO. Dlatego zastosuj sygnały sinusoidalne, które mająsame amplitude and frequency do odchylania poziomego i pionowego płyt CRO.

W przypadku kilku figur Lissajous na podstawie ich kształtu możemy bezpośrednio określić różnicę faz między dwoma sygnałami sinusoidalnymi.

• Jeśli figura Lissajous to straight line z skłonnością do $45^{\circ}$ z dodatnią osią x, a następnie phase difference między dwoma sygnałami sinusoidalnymi $0^{\circ}$. Oznacza to, że nie ma różnicy faz między tymi dwoma sygnałami sinusoidalnymi.

• Jeśli figura Lissajous to straight line z skłonnością do $135^{\circ}$ z dodatnią osią x, a następnie phase difference między dwoma sygnałami sinusoidalnymi $180^{\circ}$. Oznacza to, że te dwa sygnały sinusoidalne są poza fazą.

• Jeśli figurka Lissajous jest w środku circular shape, wtedy różnica faz między dwoma sygnałami sinusoidalnymi będzie $90^{\circ}$ lub $270^{\circ}$.

Możemy obliczyć różnicę faz między dwoma sygnałami sinusoidalnymi za pomocą wzorów, gdy figury Lissajous są elliptical shape.

• Jeśli główna oś eliptycznego kształtu figury Lissajous o kącie nachylenia leży pomiędzy $0^{\circ}$ i $90^{\circ}$ z dodatnią osią x, wówczas różnica faz między dwoma sygnałami sinusoidalnymi będzie.

$$\phi =\sin ^{-1}\left ( \frac{x_{1}}{x_{2}} \right )=\sin ^{-1}\left ( \frac{y_{1}}{y_{2}} \right )$$

• Jeśli główna oś eliptycznego kształtu figury Lissajous o kącie nachylenia leży pomiędzy $90^{\circ}$ i $180^{\circ}$ z dodatnią osią x, wówczas różnica faz między dwoma sygnałami sinusoidalnymi będzie.

$$\phi =180 - \sin ^{-1}\left ( \frac{x_{1}}{x_{2}} \right )=180 - \sin ^{-1}\left ( \frac{y_{1}}{y_{2}} \right )$$

Where,

$x_{1}$ jest odległością od początku do punktu na osi x, gdzie przecina się eliptyczny kształt Lissajous

$x_{2}$ to odległość od początku do pionowej stycznej eliptycznego kształtu figury Lissajous

$y_{1}$ jest odległością od początku do punktu na osi y, w którym eliptyczny kształt Lissajous przecina się

$y_{2}$ jest odległością od początku do poziomej stycznej eliptycznej figury Lissajous

W tym rozdziale dowiesz się, jak znaleźć częstotliwość nieznanego sygnału sinusoidalnego i różnicę faz między dwoma sygnałami sinusoidalnymi z figur Lissajous za pomocą wzorów.

Za pomocą sondy możemy podłączyć dowolny obwód testowy do oscyloskopu. Ponieważ CRO jest podstawowym oscyloskopem, nazywana jest również sondą, która jest do niego podłączonaCRO probe.

Sondę należy dobierać w taki sposób, aby nie powodowała problemów z obciążeniem obwodu testowego. Abyśmy mogli poprawnie przeanalizować obwód testowy z sygnałami na ekranie CRO.

Sondy CRO powinny mieć następujące elementy characteristics.

• Wysokiej impedancji
• Wysoka przepustowość

Plik block diagram sondy CRO pokazano na poniższym rysunku.

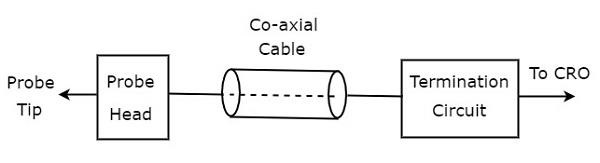
Jak pokazano na rysunku, sonda CRO składa się głównie z trzech bloków. Są to głowica sondy, kabel koncentryczny i obwód zakończeniowy. Kabel koncentryczny po prostu łączy głowicę sondy i obwód zakończeniowy.

Rodzaje sond CRO

Sondy CRO można podzielić na następujące two types.

• Sondy pasywne
• Aktywne sondy

Omówmy teraz kolejno te dwa typy sond.

Sondy pasywne

Jeśli głowica sondy składa się z elementów pasywnych, wówczas jest nazywana passive probe. Schemat obwodu sondy pasywnej pokazano na poniższym rysunku.

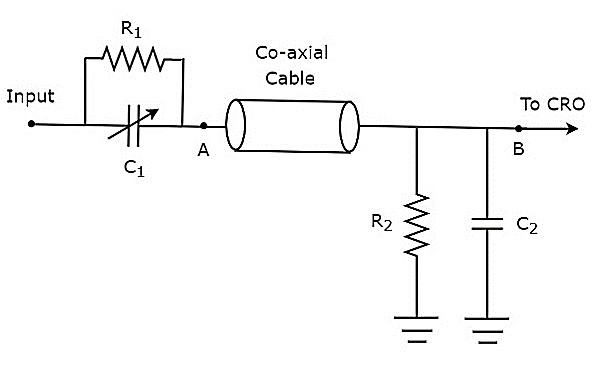
Jak pokazano na rysunku, głowica sondy składa się z równoległej kombinacji rezystorów, $R_{1}$ i zmiennym kondensatorem, $C_{1}$. Podobnie obwód terminujący składa się z równoległej kombinacji rezystora,$R_{2}$ i kondensator, $C_{2}$.

Powyższy schemat obwodu jest zmodyfikowany w postaci bridge circuit i jest to pokazane na poniższym rysunku.

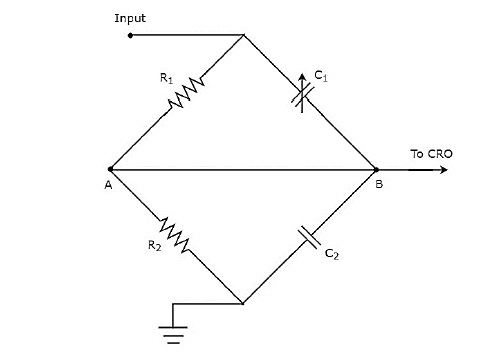
Możemy zrównoważyć mostek, dostosowując wartość zmiennego kondensatora, $c_{1}$. W kolejnych rozdziałach omówimy koncepcję mostów. Na razie rozważ następujące kwestiebalancing condition of AC bridge.

$$Z_{1}Z_{4}=Z_{2}Z_{3}$$

Substitute, impedancje $Z_{1},Z_{2}, Z_{3}$ i $Z_{4}$ tak jak $R_{1},\frac{1}{j\omega C_{1}}, R_{2}$ i $\frac{1}{j\omega C_{2}}$ odpowiednio w powyższym równaniu.

$$R_{1}\left ( \frac{1}{j \omega C_{2}} \right )=\left ( \frac{1}{j \omega C_{1}} \right )R_{2}$$

$\Rightarrow R_{1} C_{1}=R_{2} C_{2}$Równanie 1

Zgodnie z zasadą podziału napięcia otrzymamy voltage across resistor, $R_{2}$ tak jak

$$V_{0}=V_{i}\left ( \frac{R_{2}}{R_{1}+R_{2}} \right )$$

attenuation factor to stosunek napięcia wejściowego, $V_{i}$ i napięcie wyjściowe, $V_{0}$. Czyli z powyższego równania otrzymamy współczynnik tłumienia,$\alpha$ tak jak

$$\alpha = \frac{V_{i}}{V_{0}}=\frac{R_{1}+R_{2}}{R_{2}}$$

$\Rightarrow \alpha = 1+\frac{R_{1}}{R_{2}}$

$\Rightarrow \alpha-1 = \frac{R_{1}}{R_{2}}$

$\Rightarrow R_{1}= \left ( \alpha-1 \right )R_{2}$Równanie 2

Z równania 2 możemy wywnioskować, że wartość $R_{1}$ jest większa lub równa wartości ð ?? '… 2 dla wartości całkowitych z$\:\alpha > 1$.

Zastąp równanie 2 w równaniu 1.

$$\left ( \alpha-1 \right )R_{2}C_{1}=R_{2}C_{2}$$

$\Rightarrow \left ( \alpha-1 \right )C_{1} =C_{2}$

$\Rightarrow C_{1}=\frac{C_{2}}{\left ( \alpha-1 \right )}$Równanie 3

Z równania 3 możemy wywnioskować, że wartość $C_{1}$ jest mniejsza lub równa wartości $C_{2}$ dla wartości całkowitych $\alpha >1$

Example

Znajdźmy wartości $R_{1}$ i $C_{1}$ sondy mającej współczynnik tłumienia,$\alpha$ jak 10. Załóżmy, $R_{2}=1 M \Omega$ i $C_{2}=18pF$.

• Step1 - Dowiemy się o wartości $R_{1}$ zastępując wartości $\alpha$ i $R_{2}$ w równaniu 2.

$$ R_{1}=\left ( 10-1 \right )\times 1 \times 10^{6}$$

$$\Rightarrow R_{1}=9 \times 10^{6}$$

$$\Rightarrow R_{1}=9 M\Omega$$

Step 2 - Dowiemy się o wartości $C_{1}$ zastępując wartości $\alpha$ i $C_{2}$ w równaniu 3.

$$C_{1}=\frac{18\times10^{-12}}{\left ( 10-1 \right )}$$

$$\Rightarrow C_{1}=2 \times 10^{-12}$$

$$\Rightarrow C_{1}=2 pF$$

Dlatego wartości $R_{1}$ i $C_{1}$ sondy będzie $9M\Omega$ i $2pF$ odpowiednio dla podanych specyfikacji.

Aktywne sondy

Jeśli głowica sondy składa się z aktywnych elementów elektronicznych, wówczas jest nazywana active probe. Schemat blokowy aktywnej sondy pokazano na poniższym rysunku.

Jak pokazano na rysunku, głowica sondy składa się z popychacza źródła FET w kaskadzie z popychaczem emitera BJT. Popychacz źródła FET zapewnia wysoką impedancję wejściową i niską impedancję wyjściową. Natomiast celem zwolnienia emitera BJT jest uniknięcie lub wyeliminowanie niedopasowania impedancji.

Pozostałe dwie części, takie jak kabel współosiowy i obwód terminujący, pozostają takie same w sondach aktywnych i pasywnych.

Jeśli elementy elektryczne są ułożone w formie mostka lub struktury pierścieniowej, wówczas ten obwód elektryczny nazywa się a bridge. Ogólnie rzecz biorąc, most tworzy pętlę z zestawem czterech ramion lub gałęzi. Każda gałąź może zawierać jeden lub dwa komponenty elektryczne.

Rodzaje mostów

Możemy podzielić obwody mostkowe lub mosty na następujące dwie kategorie w oparciu o sygnał napięciowy, z którym mogą być obsługiwane.

• Mosty DC
• AC Bridges

Omówmy teraz pokrótce te dwa mosty.

Mosty DC

Jeśli obwód mostkowy może pracować tylko z sygnałem napięcia DC, to jest to obwód mostkowy DC lub po prostu DC bridge. Mostki prądu stałego służą do pomiaru wartości nieznanej rezystancji. Plikcircuit diagram mostka DC wygląda jak na poniższym rysunku.

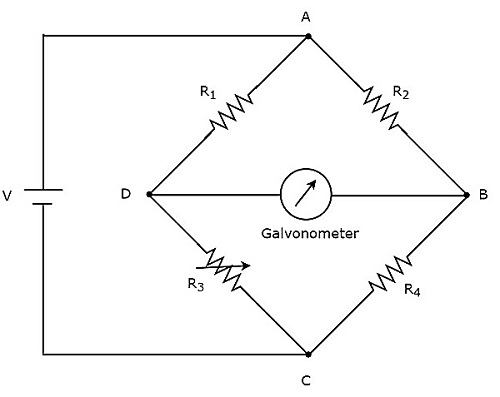
Powyższy mostek DC ma four armsa każde ramię składa się z rezystora. Wśród nich dwa rezystory mają ustalone wartości rezystancji, jeden rezystor jest rezystorem zmiennym, a drugi ma nieznaną wartość rezystancji.

Powyższy obwód mostka DC można wzbudzić za pomocą DC voltage sourceumieszczając go po jednej przekątnej. Galwanometr jest umieszczony po drugiej przekątnej mostka DC. Pokazuje pewne ugięcie, o ile most jest niezrównoważony.

Zmieniaj wartość rezystancji rezystora zmiennego, aż galwanometr wskaże zerowe (zerowe) ugięcie. Mówi się, że powyższy mostek DC jest zrównoważony. Tak więc możemy znaleźć wartośćunknown resistance za pomocą równań węzłowych.

AC Bridges

Jeśli obwód mostka może działać tylko z sygnałem napięcia AC, to mówi się, że jest to obwód mostkowy AC lub po prostu AC bridge. Mostki AC służą do pomiaru wartości nieznanej indukcyjności, pojemności i częstotliwości.

Plik circuit diagram mostka AC wygląda jak na poniższym rysunku.

Schemat obwodu mostka AC jest podobny do schematu mostka DC. Powyższy mostek AC mafour armsa każde ramię składa się z pewnej impedancji. Oznacza to, że każde ramię będzie miało jeden lub kombinację elementów pasywnych, takich jak rezystor, cewka i kondensator.

Spośród czterech impedancji dwie impedancje mają ustalone wartości, jedna impedancja jest zmienna, a druga to nieznana impedancja.

Powyższy obwód mostka AC można wzbudzić za pomocą AC voltage sourceumieszczając go po jednej przekątnej. Detektor jest umieszczony po drugiej przekątnej mostka AC. Pokazuje pewne ugięcie, o ile most jest niezrównoważony.

Powyższy obwód mostka AC można wzbudzić za pomocą AC voltage sourceumieszczając go po jednej przekątnej. Detektor jest umieszczony po drugiej przekątnej mostka AC. Pokazuje pewne ugięcie, o ile most jest niezrównoważony.

Zmieniaj wartość impedancji zmiennej impedancji, aż detektor pokaże zerowe (zerowe) odchylenie. Mówi się, że powyższy mostek AC jest zrównoważony. Tak więc możemy znaleźć wartośćunknown impedance stosując zrównoważony stan.

DC bridgesmoże pracować tylko z sygnałem napięcia stałego. Mostki prądu stałego są przydatne do pomiaru wartości nieznanej rezystancji, która występuje w mostku. Most Wheatstone'a jest przykładem mostka prądu stałego.

A teraz porozmawiajmy o Wheatstone’s Bridge w celu znalezienia nieznanej wartości oporu.

Most Wheatstone'a

Most Wheatstone'a to prosty mostek prądu stałego, który ma głównie cztery ramiona. Te cztery ramiona tworzą kształt rombu lub kwadratu, a każde ramię składa się z jednego rezystora.

Aby znaleźć wartość nieznanej rezystancji, potrzebujemy galwanometru i źródła napięcia stałego. Dlatego jeden z tych dwóch jest umieszczony na jednej przekątnej mostu Wheatstone'a, a drugi na innej przekątnej mostu Wheatstone'a.

Mostek Wheatstone'a służy do pomiaru wartości średniej rezystancji. Plikcircuit diagram mostka Wheatstone'a pokazano na poniższym rysunku.

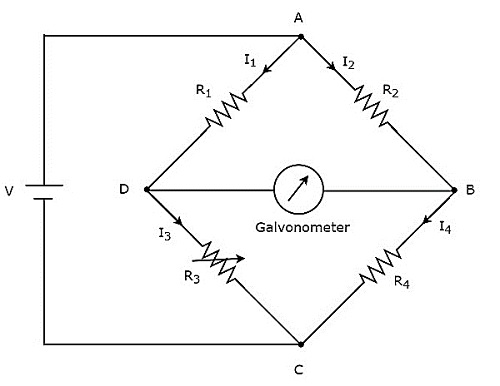
W powyższym obwodzie ramiona AB, BC, CD i DA tworzą razem a rhombuslub kwadratowy kształt. Składają się z rezystorów$R_{2}$, $R_{4}$, $R_{3}$ i $R_{1}$odpowiednio. Niech prąd przepływający przez te ramiona rezystora będzie$I_{2}$, $I_{4}$, $I_{3}$ i $I_{1}$ odpowiednio, a kierunki tych prądów pokazano na rysunku.

Ukośne ramiona DB i AC składają się odpowiednio z galwanometru i źródła napięcia stałego o wartości V. Tutaj rezystor,$R_{3}$ jest standardowym rezystorem zmiennym i rezystorem, $R_{4}$jest nieznanym rezystorem. Możemybalance the bridge, zmieniając wartość rezystancji rezystora, $R_{3}$.

Powyższy obwód mostka jest zrównoważony, gdy przez ukośne ramię DB nie płynie prąd. To znaczy, że jestno deflection w galwanometrze, gdy mostek jest wyważony.

Mostek zostanie wyważony, gdy nastąpi następne two conditions zadowoleni.

• Napięcie na ramieniu AD jest równe napięciu na ramieniu AB. to znaczy,

$$V_{AD}=V_{AB}$$

$\Rightarrow I_{1}R_{1}=I_{2}R_{2}$Równanie 1

• Napięcie na ramieniu DC jest równe napięciu na ramieniu BC. to znaczy,

$$V_{DC}=V_{BC}$$

$\Rightarrow I_{3}R_{3}=I_{4}R_{4}$Równanie 2

Z powyższych dwóch warunków równoważenia otrzymamy, co następuje two conclusions.

• Prąd przepływający przez ramię AD będzie równy prądowi ramienia DC. to znaczy,

$$I_{1}=I_{3}$$

• Prąd przepływający przez ramię AB będzie równy prądowi z ramienia BC. to znaczy,

$$I_{2}=I_{4}$$

Weź stosunek równania 1 i równania 2.

$\frac{I_{1}R_{1}}{I_{3}R_{3}}=\frac{I_{2}R_{2}}{I_{4}R_{4}}$Równanie 3

Zastąpić, $I_{1}=I_{3}$ i $I_{2}=I_{4}$ w równaniu 3.

$$\frac{I_{3}R_{1}}{I_{3}R_{3}}=\frac{I_{4}R_{2}}{I_{4}R_{4}}$$

$$\Rightarrow \frac{R_{1}}{R_{3}}=\frac{R_{2}}{R_{4}}$$

$$\Rightarrow R_{4}=\frac{R_{2}R_{3}}{R_{1}}$$

Zastępując znane wartości rezystorów $R_{1}$, $R_{2}$ i $R_{3}$ w powyższym równaniu otrzymamy value of resistor,$R_{4}$.

W tym rozdziale omówimy mostki AC, których można użyć do pomiaru indukcyjności. Mostki AC działają tylko z sygnałem napięcia AC. Plikcircuit diagram mostka AC pokazano na poniższym rysunku.

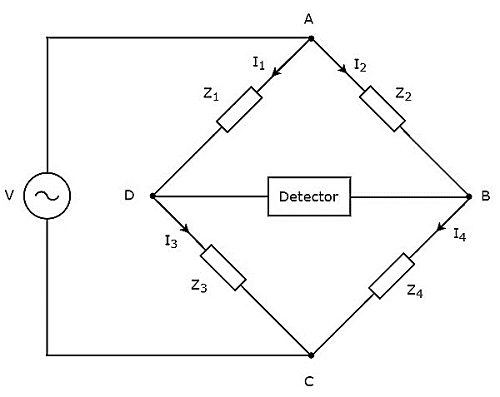
Jak pokazano na powyższym rysunku, mostek AC składa się głównie z czterech ramion, które są połączone w romb lub square shape. Wszystkie te ramiona mają pewną impedancję.

Do znalezienia wartości o nieznanej impedancji potrzebny jest również detektor i źródło napięcia zmiennego. Stąd jeden z tych dwóch jest umieszczony na jednej przekątnej mostka AC, a drugi na drugiej przekątnej mostka AC. Stan wyważenia mostu Wheatstone'a jako -

$$R_{4}=\frac{R_{2}R_{3}}{R_{1}}$$

Otrzymamy balancing condition of AC bridge, po prostu zastępując R przez Z w powyższym równaniu.

$$Z_{4}=\frac{Z_{2}Z_{3}}{Z_{1}}$$

$\Rightarrow Z_{1}Z_{4}=Z_{2}Z_{3}$

Tutaj, $Z_{1}$ i $Z_{2}$są stałymi impedancjami. Natomiast,$Z_{3}$ jest standardową zmienną impedancją i $Z_{4}$ jest nieznaną impedancją.

Note - Możemy wybrać dowolne dwie z tych czterech impedancji jako stałe impedancje, jedną impedancję jako standardową zmienną impedancję, a drugą jako nieznaną impedancję w oparciu o aplikację.

Poniżej znajdują się dwa mostki AC, które można wykorzystać do pomiaru inductance.

• Most Maxwella
• Hay's Bridge

Omówmy teraz kolejno te dwa mostki AC.

Most Maxwella

Most Maxwella to mostek prądu przemiennego posiadający cztery ramiona, które są połączone w kształcie rombu lub square shape. Dwa ramiona tego mostka składają się z pojedynczego rezystora, jedno ramię składa się z szeregowej kombinacji rezystora i cewki, a drugie ramię składa się z równoległej kombinacji rezystora i kondensatora.

Do znalezienia wartości nieznanej impedancji wykorzystuje się detektor AC i źródło napięcia AC. Dlatego jeden z tych dwóch jest umieszczony na jednej przekątnej mostu Maxwella, a drugi na drugiej przekątnej mostu Maxwella.

Mostek Maxwella służy do pomiaru wartości średniej indukcyjności. Plikcircuit diagram mostu Maxwella pokazano na poniższym rysunku.

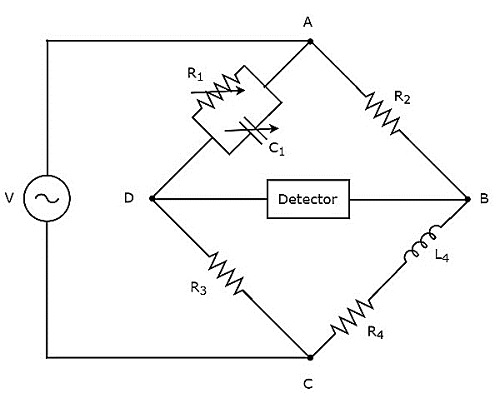
W powyższym obwodzie ramiona AB, BC, CD i DA tworzą razem kształt rombu lub kwadratu. Ramiona AB i CD składają się z rezystorów,$R_{2}$ i $R_{3}$odpowiednio. Ramię BC składa się z szeregowej kombinacji rezystorów,$R_{4}$ i induktor, $L_{4}$. Ramię DA składa się z równoległej kombinacji rezystorów,$R_{1}$ i kondensator, $C_{1}$.

Pozwolić, $Z_{1}, Z_{2}, Z_{3}$ i $Z_{4}$są impedancjami ramion odpowiednio DA, AB, CD i BC. Plikvalues of these impedances będzie

$$Z_{1}=\frac{R_{1}\left ( \frac{1}{j\omega C_{1}} \right )}{R_{1}+\frac{1}{j\omega C_{1}}}$$

$$\Rightarrow Z_{1}=\frac{R_{1}}{1+j \omega R_{1}C_{1}}$$

$Z_{2}=R_{2}$

$Z_{3}=R_{3}$

$Z_{4}=R_{4}+j \omega L_{4}$

Substitute te wartości impedancji w następującym stanie wyważenia mostka AC.

$$Z_{4}=\frac{Z_{2}Z_{3}}{Z_{1}}$$

$$R_{4}+j\omega L_{4}=\frac{R_{2}R_{3}}{\left ( {\frac{R_{1}}{1+j \omega R_{1}C_{1}}} \right )}$$

$\Rightarrow R_{4}+j\omega L_{4}=\frac{R_{2}R_{3}\left (1+j \omega R_{1}C_{1} \right )}{R_{1}}$

$\Rightarrow R_{4}+j\omega L_{4}=\frac{R_{2}R_{3}}{R_{1}}+\frac{j \omega R_{1}C_{1}R_{2}R_{3}}{R_{1}}$

$\Rightarrow R_{4}+j\omega L_{4}=\frac{R_{2}R_{3}}{R_{1}}+j \omega C_{1}R_{2}R_{3}$

Przez comparing otrzymamy odpowiednie wyrażenia rzeczywiste i urojone z powyższego równania

$R_{4}=\frac{R_{2}R_{3}}{R_{1}}$Równanie 1

$L_{4}=C_{1}R_{2}R_{3}$Równanie 2

Zastępując wartości rezystorów $R_{1}$, $R_{2}$ i $R_{3}$ w równaniu 1 otrzymamy wartość rezystora, $R_{4}$. Podobnie, zastępując wartość kondensatora,$C_{1}$ i wartości rezystorów, $R_{2}$ i $R_{3}$ w równaniu 2 otrzymamy wartość induktora, $L_{4}$.

Plik advantage mostka Maxwella jest to, że obie wartości rezystora, $R_{4}$ i induktor, $L_{4}$ są niezależne od wartości częstotliwości.

Hay's Bridge

Mostek Haya to zmodyfikowana wersja mostka Maxwella, którą otrzymujemy modyfikując ramię, które składa się z równoległej kombinacji rezystora i kondensatora w ramieniu, które składa się z szeregowej kombinacji rezystora i kondensatora w mostku Maxwella.

Mostek Hay służy do pomiaru wartości wysokiej indukcyjności. Plikcircuit diagram mostu Hay pokazano na poniższym rysunku.

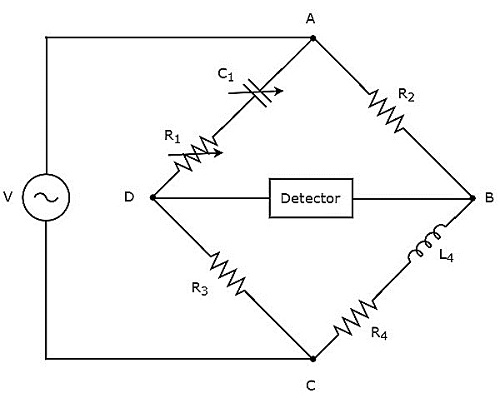
W powyższym obwodzie ramiona AB, BC, CD i DA tworzą razem kształt rombu lub kwadratu. Ramiona AB i CD składają się z rezystorów,$R_{2}$ i $R_{3}$odpowiednio. Ramię BC składa się z szeregowej kombinacji rezystorów,$R_{4}$ i induktor, $L_{4}$. Ramię DA składa się z szeregowej kombinacji rezystorów,$R_{1}$ i kondensator, $C_{1}$.

Pozwolić, $Z_{1}, Z_{2}, Z_{3}$ i $Z_{4}$są impedancjami ramion odpowiednio DA, AB, CD i BC. Plikvalues of these impedances będzie

$$Z_{1}=R_{1}+\frac{1}{j \omega C_{1}}$$

$\Rightarrow Z_{1}=\frac{1+j \omega R_{1}C_{1}}{j \omega C_{1}}$

$Z_{2}=R_{2}$

$Z_{3}=R_{3}$

$Z_{4}=R_{4}+j \omega L_{4}$

Substitute te wartości impedancji w następującym stanie wyważenia mostka AC.

$$Z_{4}=\frac{Z_{2}Z_{3}}{Z_{1}}$$

$R_{4}+j \omega L_{4}=\frac{R_{2}R_{3}}{\left ( \frac{1+j \omega R_{1}C_{1}}{j \omega C_{1}}\right )}$

$R_{4}+j \omega L_{4}=\frac{R_{2}R_{3}j \omega C_{1}}{\left ( 1+j \omega R_{1}C_{1}\right )}$

Pomnóż licznik i mianownik wyrażenia po prawej stronie powyższego równania przez $1 - j \omega R_{1}C_{1}$.

$\Rightarrow R_{4}+j \omega L_{4}=\frac{R_{2}R_{3}j \omega C_{1}}{\left ( 1+j \omega R_{1}C_{1}\right )}\times \frac{\left (1 - j \omega R_{1}C_{1} \right )}{\left (1 - j \omega R_{1}C_{1} \right )}$

$\Rightarrow R_{4}+j \omega L_{4}=\frac{\omega^{2}{C_{1}}^{2}R_{1}R_{2}R_{3}+j \omega R_{2}R_{3}C_{1}}{\left ( 1+\omega^{2}{R_{1}}^{2}{C_{1}}^{2}\right )}$

Przez comparing otrzymamy odpowiednie wyrażenia rzeczywiste i urojone z powyższego równania

$R_{4}= \frac{\omega^{2}{C_{1}}^{2}R_{1}R_{2}R_{3}}{\left ( 1+\omega^{2}{R_{1}}^{2}{C_{1}}^{2}\right )}$Równanie 3

$L_{4}= \frac{R_{2}R_{3}C_{1}}{\left ( 1+\omega^{2}{R_{1}}^{2}{C_{1}}^{2}\right )}$Równanie 4

Zastępując wartości $R_{1}, R_{2}, R_{3}, C_{1}$ i $\omega$ w równaniu 3 i równaniu 4 otrzymamy wartości rezystora, $R_{4}$ i induktor, $L_{4}$.

W poprzednim rozdziale omówiliśmy dwa mostki AC, których można użyć do pomiaru indukcyjności. W tym rozdziale omówimy następujące kwestietwo AC bridges.

• Schering Bridge
• Most Wiednia

Te dwa mostki mogą służyć do pomiaru odpowiednio pojemności i częstotliwości.

Schering Bridge

Most Schering to mostek prądu przemiennego mający cztery ramiona, które są połączone w formie rombu lub square shape, którego jedno ramię składa się z pojedynczego rezystora, jedno ramię składa się z szeregowej kombinacji rezystora i kondensatora, jedno ramię składa się z pojedynczego kondensatora, a drugie ramię składa się z równoległej kombinacji rezystora i kondensatora.

Detektor prądu zmiennego i źródło napięcia zmiennego są również wykorzystywane do wyznaczania wartości nieznanej impedancji, stąd jeden z nich jest umieszczony na jednej przekątnej mostka Scheringa, a drugi na drugiej przekątnej mostka Scheringa.

Mostek Scheringa służy do pomiaru wartości pojemności. Plikcircuit diagram mostu Schering pokazano na poniższym rysunku.

W powyższym obwodzie ramiona AB, BC, CD i DA tworzą razem romb lub square shape. Ramię AB składa się z rezystora,$R_{2}$. Ramię BC składa się z szeregu kombinacji rezystorów,$R_{4}$ i kondensator, $C_{4}$. Ramię CD składa się z kondensatora,$C_{3}$. Ramię DA składa się z równoległej kombinacji rezystorów,$R_{1}$ i kondensator, $C_{1}$.

Pozwolić, $Z_{1}$, $Z_{2}$,$Z_{3}$ i $Z_{4}$są impedancjami ramion odpowiednio DA, AB, CD i BC. Plikvalues of these impedances będzie

$Z_{1}=\frac{R_{1}\left ( \frac{1}{j \omega C_{1}} \right )}{R_{1}+\frac{1}{j \omega C_{1}}}$

$\Rightarrow Z_{1}=\frac{R_{1}}{1+j \omega R_{1}C_{1}}$

$Z_{2}=R_{2}$

$Z_{3}=\frac{1}{j \omega C_{3}}$

$Z_{4}=R_{4}+\frac{1}{j \omega C_{4}}$

$\Rightarrow Z_{4}=\frac{1+j \omega R_{4}C_{4}}{j \omega C_{4}}$

Substitute te wartości impedancji w następującym stanie wyważenia mostka AC.

$$Z_{4}=\frac{Z_{2}Z_{3}}{Z_{1}}$$

$$\frac{1+j \omega R_{4}C_{4}}{j \omega C_{4}}=\frac{R_{2}\left (\frac{1}{j \omega C_{3}} \right )}{\frac{R_{1}}{1+j \omega R_{1}C_{1}}}$$

$\Rightarrow \frac{1+j \omega R_{4}C_{4}}{j \omega C_{4}}=\frac{R_{2}\left ( 1+j \omega R_{1}C_{1} \right )}{j \omega R_{1}C_{3}}$

$\Rightarrow \frac{1+j \omega R_{4}C_{4}}{C_{4}}=\frac{R_{2}\left ( 1+j \omega R_{1}C_{1} \right )}{R_{1}C_{3}}$

$\Rightarrow \frac{1}{C_{4}}+j \omega R_{4}=\frac{R_{2}}{R_{1}C_{3}}+\frac{j\omega C_{1}R_{2}}{C_{3}}$

Przez comparing otrzymamy odpowiednie wyrażenia rzeczywiste i urojone z powyższego równania

$C_{4}=\frac{R_{1}C_{3}}{R_{2}}$Równanie 1

$R_{4}=\frac{C_{1}R_{2}}{C_{3}}$Równanie 2

Zastępując wartości $R_{1}, R_{2}$ i $C_{3}$ w równaniu 1 otrzymamy wartość kondensatora, $C_{4}$. Podobnie, zastępując wartości$R_{2}, C_{1}$ i $C_{3}$ w równaniu 2 otrzymamy wartość rezystora, $R_{4}$.

Plik advantage mostka Scheringa jest to, że obie wartości rezystora, $R_{4}$ i kondensator, $C_{4}$ są niezależne od wartości częstotliwości.

Most Wiednia

Wien’s bridgeto mostek prądu przemiennego posiadający cztery ramiona, które są połączone w kształcie rombu lub kwadratu. Dwa ramiona składają się z pojedynczego rezystora, jedno ramię składa się z równoległej kombinacji rezystora i kondensatora, a drugie ramię składa się z szeregowej kombinacji rezystora i kondensatora.

Do znalezienia wartości częstotliwości wymagany jest również detektor prądu zmiennego i źródło napięcia zmiennego. Stąd jeden z tych dwóch jest umieszczony na jednej przekątnej mostu Wiednia, a drugi na drugiej przekątnej mostu Wiednia.

Plik circuit diagram mostu Wiena pokazano na poniższym rysunku.

W powyższym obwodzie ramiona AB, BC, CD i DA tworzą razem romb lub square shape. Ramiona AB i BC składają się z rezystorów,$R_{2}$ i $R_{4}$odpowiednio. Ramię CD składa się z równoległej kombinacji rezystorów,$R_{3}$ i kondensator, $C_{3}$. Ramię DA składa się z szeregowej kombinacji rezystorów,$R_{1}$ i kondensator, $C_{1}$.

Pozwolić, $Z_{1}, Z_{2}, Z_{3}$ i $Z_{4}$są impedancjami ramion odpowiednio DA, AB, CD i BC. Plikvalues of these impedances będzie

$$Z_{1}=R_{1}+\frac{1}{j \omega C_{1}}$$

$$\Rightarrow Z_{1}=\frac{1+j \omega R_{1}C_{1}}{j \omega C_{1}}$$

$Z_{2}=R_{2}$

$$Z_{3}=\frac{R_{3}\left (\frac{1}{j \omega C_{3}} \right )}{R_{3}+\frac{1}{j \omega C_{3}}}$$

$$\Rightarrow Z_{3}= \frac{R_{3}}{1+j \omega R_{3}C_{3}}$$

$Z_{4}=R_{4}$

Substitute te wartości impedancji w następującym stanie wyważenia mostka AC.

$$Z_{1}Z_{4}=Z_{2}Z_{3}$$

$$\left (\frac{1+j \omega R_{1}C_{1}}{j \omega C_{1}} \right )R_{4}=R_{2}\left (\frac{R_{3}}{1+j \omega R_{3}C_{3}} \right )$$

$\Rightarrow \left (1+j \omega R_{1}C_{1}\right )\left (1+j \omega R_{3}C_{3}\right )R_{4}=j \omega C_{1}R_{2}R_{3}$

$\Rightarrow \left (1+j \omega R_{3}C_{3}+j \omega R_{1}C_{1}-\omega^{2}R_{1}R_{3}C_{1}C_{3}\right )R_{4}=j \omega C_{1}R_{2}R_{3}$

$\Rightarrow R_{4}\left ( \omega^{2}R_{1}R_{3}C_{1}C_{3} \right )+j \omega R_{4}\left (R_{3}C_{3}+R_{1}C_{1} \right )=j \omega C_{1}R_{2}R_{3}$

Equate odpowiedni real terms powyższego równania.

$$R_{4}\left (1- \omega^{2}R_{1}R_{3}C_{1}C_{3} \right )=0$$

$\Rightarrow 1- \omega^{2}R_{1}R_{3}C_{1}C_{3} =0$

$\Rightarrow 1= \omega^{2}R_{1}R_{3}C_{1}C_{3}$

$\omega = \frac{1}{\sqrt{R_{1}R_{3}C_{1}C_{3}}}$

Substitute, $\omega = 2 \pi f$ w powyższym równaniu.

$$\Rightarrow 2 \pi f= \frac{1}{\sqrt{R_{1}R_{3}C_{1}C_{3}}}$$

$\Rightarrow f= \frac{1}{2 \pi\sqrt{R_{1}R_{3}C_{1}C_{3}}}$

Możemy znaleźć wartość częstotliwości, $f$ źródła napięcia przemiennego, zastępując wartości $R_{1}, R_{3}, C_{1}$ i $C_{3}$ w powyższym równaniu.

Gdyby $R_{1}=R_{3}=R$ i $C_{1}=C_{3}=C$, wtedy możemy znaleźć wartość częstotliwości, $f$ źródła napięcia przemiennego za pomocą następującego wzoru.

$$f=\frac{1}{2\pi RC}$$

Most Weina służy głównie do znajdowania frequency value zakresu AF.

Zasadniczo przetwornik przekształca jedną formę energii w inną formę energii. Przetwornik, który przekształca nieelektryczną formę energii w elektryczną postać energii, jest znany jakoelectrical transducer. Plikblock diagram przetwornika elektrycznego pokazano na poniższym rysunku.

Jak pokazano na rysunku, przetwornik elektryczny wytworzy sygnał wyjściowy zawierający energię elektryczną. Wyjście przetwornika elektrycznego jest równoważne wejściu, które zawiera energię nieelektryczną.

Rodzaje przetworników elektrycznych

Głównie przetworniki elektryczne można podzielić na następujące two types.

• Aktywne przetworniki
• Przetworniki pasywne

Omówmy teraz pokrótce te dwa typy przetworników.

Aktywne przetworniki

Przetwornik, który może wytwarzać jedną z wielkości elektrycznych, takich jak napięcie i prąd, jest znany jako active transducer. Jest również nazywany przetwornikiem samoczynnym, ponieważ nie wymaga zewnętrznego zasilania.

Plik block diagram aktywnego przetwornika pokazano na poniższym rysunku.

Jak pokazano na rysunku, aktywny przetwornik wytworzy wielkość elektryczną (lub sygnał), która jest równoważna nieelektrycznej wielkości wejściowej (lub sygnałowi).

Examples

Poniżej znajdują się przykłady aktywnych przetworników.

• Przetwornik piezoelektryczny
• Przetwornik fotoelektryczny
• Przetwornik termoelektryczny

Omówimy te aktywne przetworniki w następnym rozdziale.

Przetworniki pasywne

Przetwornik, który nie może wytwarzać wielkości elektrycznych, takich jak napięcie i prąd, jest znany jako passive transducer. Ale powoduje zmianę jednego z elementów pasywnych, takich jak rezystor (R), cewka indukcyjna (L) i kondensator (C). Przetwornik pasywny wymaga zewnętrznego zasilania.

Plik block diagram przetwornika pasywnego pokazano na poniższym rysunku.

Jak pokazano na rysunku, przetwornik pasywny będzie wytwarzał zmiany w elemencie pasywnym zgodnie ze zmianami nieelektrycznej wielkości wejściowej (lub sygnału).

Examples

Poniżej podano przykłady przetworników pasywnych.

• Przetwornik rezystancyjny
• Przetwornik indukcyjny
• Przetwornik pojemnościowy

Omówimy te pasywne przetworniki w dalszych rozdziałach.

Active transducerjest przetwornikiem, który przekształca wielkość nieelektryczną w wielkość elektryczną. Rozważmy wielkości nieelektryczne, takie jak ciśnienie, oświetlenie i temperatura. W związku z tym otrzymamy następujące trzy aktywne przetworniki w zależności od wybranej przez nas wielkości nieelektrycznej.

• Przetwornik piezoelektryczny
• Przetwornik fotoelektryczny
• Przetwornik termoelektryczny

Omówmy teraz kolejno te trzy aktywne przetworniki.

Przetwornik piezoelektryczny

Mówi się, że jest to aktywny przetwornik piezo electric transducer, kiedy wytwarza wielkość elektryczną równoważną ciśnieniu wejściowemu. Następujące trzy substancje wykazują efekt piezoelektryczny.

• Quartz
• Sole Rochelle
• Tourmaline

Efekt piezoelektryczny wykazywany przez te trzy substancje to sole turmalinu, kwarcu i Rochelle, w kolejności rosnącej. W porządku rosnącym wytrzymałości mechanicznej tych trzech substancji są sole Rochelle, kwarc, turmalin.

Quartz jest używany jako przetwornik piezoelektryczny, ponieważ wykazuje umiarkowany efekt piezoelektryczny i ma umiarkowaną wytrzymałość mechaniczną wśród tych trzech substancji piezoelektrycznych.

Przetwornik kwarcowy

Plik circuit diagramprzetwornika kwarcowego pokazano na poniższym rysunku. Jak pokazano na rysunku, kryształ kwarcu jest umieszczony pomiędzy podstawą a członem sumującym siły. Napięcie wyjściowe można mierzyć na metalowych elektrodach, które są umieszczone po dwóch stronach kryształu kwarcu.

Plik output voltage, $V_{0}$ powyższego przetwornika ciśnienia będzie

$$V_{0}=\frac{Q}{C}$$

Przetwornik fotoelektryczny

Mówi się, że przetwornik aktywny jest przetwornikiem fotoelektrycznym, gdy wytwarza wielkość elektryczną, która jest równoważna oświetleniu wejścia światła. Plikcircuit diagram przetwornika fotoelektrycznego pokazano na poniższym rysunku.

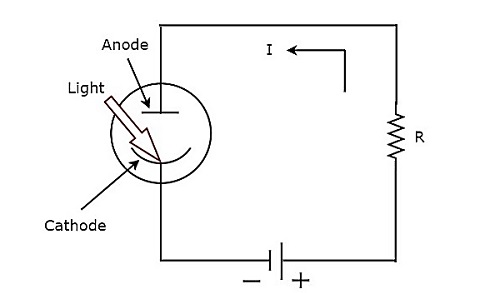
Plik working przetwornika fotoelektrycznego wymieniono poniżej.

• Step1 - Przetwornik fotoelektryczny uwalnia elektrony, gdy światło pada na jego katodę.

• Step2 - Przetwornik fotoelektryczny wytwarza w obwodzie prąd I na skutek przyciągania elektronów do anody.

Możemy znaleźć sensitivity przetwornika fotoelektrycznego za pomocą następującego wzoru.

$$S=\frac{I}{i}$$

Gdzie,

$S$ to czułość fotoelektrycznego przetwornika

$I$ jest prądem wyjściowym fotoelektrycznego przetwornika

$i$ jest oświetleniem wejścia światła fotoelektrycznego przetwornika

Przetwornik termoelektryczny

Mówi się, że jest to aktywny przetwornik thermo electric transducer, kiedy wytwarza wielkość elektryczną, która jest równoważna wejściu temperatury. Poniższe dwa przetworniki są przykładami przetworników termoelektrycznych.

• Przetwornik termistorowy
• Przetwornik termopary

Omówmy teraz kolejno te dwa przetworniki.

Przetwornik termistorowy

Rezystor, który zależy od temperatury, nazywany jest rezystorem termicznym. Krótko mówiąc, nazywa sięThermistor. Współczynnik temperaturowy termistora jest ujemny. Oznacza to, że wraz ze wzrostem temperatury rezystancja termistora maleje.

Mathematically, zależność między rezystancją termistora a temperaturą można przedstawić jako

$$R_{1}=R_{2}e^\left ( \beta \left [ \frac{1}{T_{1}}-\frac{1}{T_{2}} \right ] \right )$$

Where,

$R_{1}$ jest oporem termistora w temperaturze ${T_{1}}^{0}K$

$R_{2}$ jest oporem termistora w temperaturze ${T_{2}}^{0}K$

$\beta$ jest stałą temperaturą

Plik advantage Przetwornik termistorowy zapewnia szybką i stabilną odpowiedź.

Przetwornik termopary

Przetwornik termopary wytwarza napięcie wyjściowe dla odpowiedniej zmiany temperatury na wejściu. Jeśli dwa druty z różnych metali są połączone ze sobą w celu utworzenia dwóch połączeń, wówczas wywoływana jest cała konfiguracjaThermocouple. Schemat obwodu podstawowej termopary pokazano poniżej -

Powyższa termopara ma dwa metale, A i B oraz dwa złącza, 1 i 2. Rozważ stałą temperaturę odniesienia, $T_{2}$ na skrzyżowaniu 2. Niech temperatura na skrzyżowaniu 1 wynosi $T_{1}$. Termopara generuje plikemf (elektromotoryczna siła napędowa), ilekroć wartości $T_{1}$ i $T_{2}$ są różne.

Oznacza to, że termopara generuje emf, ilekroć występuje różnica temperatur między dwoma złączami 1 i 2 i jest ona wprost proporcjonalna do różnicy temperatur między tymi dwoma złączami. Mathematically, można go przedstawić jako

$$e \alpha \left ( T_{1}-T_{2} \right )$$

Gdzie,

$e$ jest emf generowanym przez termoparę

Powyższy obwód termopary można przedstawić, jak pokazano na poniższym rysunku, dla praktycznych zastosowań.

Część obwodu, która znajduje się pomiędzy gorącymi i zimnymi złączami, w tym te dwa złącza, jest równoważnym modelem podstawowej termopary. Galwanometr PMMC jest podłączony w poprzek zimnego złącza i odchyla się zgodnie z emf generowanym na zimnym złączu.Thermocouple transducer jest najczęściej używanym przetwornikiem termoelektrycznym.

passive transducerjest przetwornikiem, który wytwarza zmienność elementu biernego. Rozważymy elementy pasywne, takie jak rezystor, cewka i kondensator. Stąd w zależności od wybranego przez nas elementu pasywnego otrzymamy następujące trzy przetworniki pasywne.

• Przetwornik rezystancyjny
• Przetwornik indukcyjny
• Przetwornik pojemnościowy

Omówmy teraz kolejno te trzy przetworniki pasywne.

Przetwornik rezystancyjny

Mówi się, że przetwornik pasywny to resistive transducer, kiedy powoduje zmianę (zmianę) wartości oporu. następujący wzór dlaresistance, R metalowego przewodnika.

$$R=\frac{\rho \:l}{A}$$

Gdzie,

$\rho$ jest rezystywnością przewodnika

$l$ jest długością przewodnika

$A$ to pole przekroju poprzecznego przewodnika

Wartość rezystancji zależy od trzech parametrów $\rho, l$ & $A$. Więc możemy zrobićresistive transducers na podstawie zmiany jednego z trzech parametrów $\rho, l$ & $A$. Zmiana dowolnego z tych trzech parametrów zmienia wartość rezystancji.

• Opór, R jest wprost proporcjonalny do resistivity dyrygenta, $\rho$. Tak więc, jako rezystywność przewodnika,$\rho$zwiększa wartość oporu, R również rośnie. Podobnie, jak rezystywność przewodnika,$\rho$ zmniejsza wartość oporu, R również maleje.

• Opór, R jest wprost proporcjonalny do length dyrygenta, $l$. Tak więc, jako długość przewodnika,$l$zwiększa wartość oporu, R również rośnie. Podobnie, jak długość przewodu,$l$ zmniejsza wartość oporu, R również maleje.

• Opór, R jest odwrotnie proporcjonalny do cross sectional area dyrygenta, $A$. Tak więc, jako pole przekroju poprzecznego przewodnika,$A$zwiększa wartość oporu, R maleje. Podobnie, jak pole przekroju poprzecznego przewodnika,$A$ zmniejsza wartość oporu, R wzrasta.

Przetwornik indukcyjny

Mówi się, że pasywny przetwornik to inductive transducer, kiedy powoduje zmianę (zmianę) wartości indukcyjności. następujący wzór dlainductance, L cewki.

$L=\frac{N^{2}}{S}$Równanie 1

Gdzie,

$N$ to liczba zwojów cewki

$S$ to liczba zwojów cewki

następujący wzór dla reluctance, S cewki.

$S=\frac{l}{\mu A}$Równanie 2

Gdzie,

$l$ to długość obwodu magnetycznego

$\mu$ to przepuszczalność rdzenia

$A$ to obszar obwodu magnetycznego, przez który przepływa strumień

Zastąp równanie 2 w równaniu 1.

$$L=\frac{N^{2}}{\left (\frac{l}{\mu A} \right )}$$

$\Rightarrow L=\frac{N^{2}\mu A}{l}$Równanie 3

Z równania 1 i równania 3 możemy wywnioskować, że wartość indukcyjności zależy od trzech parametrów $N,S$ & $\mu$. Więc możemy zrobićinductive transducers na podstawie zmiany jednego z trzech parametrów $N,S$ & $\mu$. Ponieważ zmiana dowolnego z tych trzech parametrów zmienia wartość indukcyjności.

• Indukcyjność, L jest wprost proporcjonalna do kwadratu number of turns of coil. Tak więc, jako liczba zwojów cewki,$N$ zwiększa wartość indukcyjności, $L$również wzrasta. Podobnie, jak liczba zwojów cewki,$N$ zmniejsza wartość indukcyjności, $L$ również maleje.

• Indukcyjność, $L$ jest odwrotnie proporcjonalna do reluctance of coil, $S$. Tak więc, jako niechęć cewki,$S$ zwiększa wartość indukcyjności, $L$maleje. Podobnie jak reluktancja cewki,$S$ zmniejsza wartość indukcyjności, $L$ wzrasta.

• Indukcyjność, L jest wprost proporcjonalna do permeability of core, $\mu$. Tak więc, jako przepuszczalność rdzenia,$\mu$zwiększa wartość indukcyjności, wzrasta również L. Podobnie, jak przepuszczalność rdzenia,$\mu$ zmniejsza wartość indukcyjności, L również maleje.

Przetwornik pojemnościowy

Mówi się, że przetwornik pasywny to capacitive transducer, kiedy powoduje zmianę (zmianę) wartości pojemności. następujący wzór dlacapacitance, C równoległego kondensatora płytowego.

$$C=\frac{\varepsilon A}{d}$$

Gdzie,

$\varepsilon$ jest przenikalnością cieplną lub stałą dielektryczną

$A$ to efektywna powierzchnia dwóch płyt

$d$ to efektywna powierzchnia dwóch płyt

Wartość pojemności zależy od trzech parametrów $\varepsilon, A$ & $d$. Więc możemy zrobićcapacitive transducers na podstawie zmiany jednego z trzech parametrów$\varepsilon, A$ & $d$. Ponieważ zmiana dowolnego z tych trzech parametrów zmienia wartość pojemności.

• Pojemność, C jest wprost proporcjonalna do permittivity, $\varepsilon$. Tak więc, jako przenikalność,$\varepsilon$zwiększa wartość pojemności, wzrasta również C. Podobnie, jak przenikalność,$\varepsilon$ zmniejsza wartość pojemności, C również maleje.

• Pojemność, C jest wprost proporcjonalna do effective area of two plates, $A$. Zatem jako efektywna powierzchnia dwóch płyt$A$zwiększa wartość pojemności, wzrasta również C. Podobnie, jako efektywna powierzchnia dwóch płyt,$A$ zmniejsza wartość pojemności, C również maleje.

• Pojemność, C jest odwrotnie proporcjonalna do distance between two plates, $d$. Tak więc, jako odległość między dwiema płytami,$d$zwiększa wartość pojemności, C maleje. Podobnie, jako odległość między dwiema płytami,$d$ zmniejsza wartość pojemności, zwiększa się C.

W tym rozdziale omówiliśmy trzy przetworniki pasywne. W następnym rozdziale omówimy przykład dla każdego przetwornika pasywnego.

Plik physical quantitiestakie jak przemieszczenie, prędkość, siła, temperatura itp. są wielkościami nieelektrycznymi. aktywny przetwornik przekształca wielkość fizyczną w sygnał elektryczny. Natomiast przetwornik pasywny przekształca wielkość fizyczną w zmienność elementu pasywnego.

Zatem na podstawie wymagań możemy wybrać przetwornik aktywny lub przetwornik pasywny. W tym rozdziale omówimy, jak mierzyć przemieszczenie za pomocą pasywnego przetwornika. Jeśli ciało porusza się z jednego punktu do drugiego w linii prostej, wówczas nazywana jest długość między tymi dwoma punktamidisplacement.

Mamy następujące three passive transducers

• Przetwornik rezystancyjny
• Przetwornik indukcyjny
• Przetwornik pojemnościowy

Omówmy teraz pomiar przemieszczenia za pomocą tych trzech pasywnych przetworników jeden po drugim.

Pomiar przemieszczenia za pomocą przetwornika rezystancyjnego

Plik circuit diagram przetwornika rezystancyjnego, który służy do pomiaru przemieszczenia pokazano na poniższym rysunku.

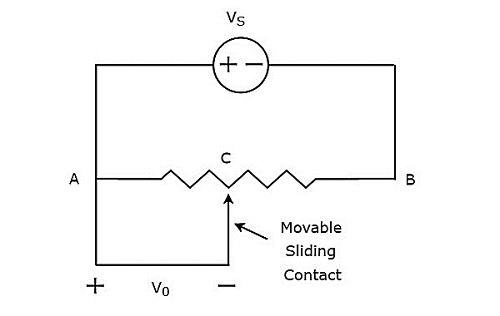
Powyższy obwód składa się z potencjometru i źródła napięcia, $V_{S}$. Można powiedzieć, że te dwa są połączone równolegle względem punktów A i B. Potencjometr ma styk ślizgowy, który można zmieniać. Zatem punkt C jest zmienny. W powyższym obwodzieoutput voltage, $V_{0}$ mierzy się w punktach A i C.

Mathematically, zależność między napięciami i odległościami można przedstawić jako

$$\frac{V_{0}}{V_{S}}=\frac{AC}{AB}$$

Dlatego należy połączyć korpus, którego przemieszczenie ma być zmierzone, z kontaktem ślizgowym. Tak więc za każdym razem, gdy ciało porusza się w linii prostej, punkt C również się zmienia. Z tego powodu napięcie wyjściowe,$V_{0}$ również odpowiednio się zmienia.

W tym przypadku przemieszczenie możemy znaleźć mierząc napięcie wyjściowe, $V_{0}$.

Pomiar przemieszczenia za pomocą przetwornika indukcyjnego

Plik circuit diagram przetwornika indukcyjnego, który służy do pomiaru przemieszczenia pokazano na poniższym rysunku.

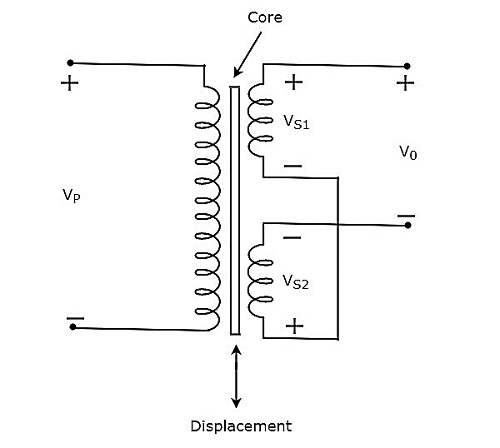
Transformator obecny w powyższym obwodzie ma uzwojenie pierwotne i dwa uzwojenia wtórne. Tutaj punkty końcowe dwóch uzwojeń wtórnych są ze sobą połączone. Możemy więc powiedzieć, że te dwa uzwojenia wtórne są połączoneseries opposition.

Napięcie, $V_{P}$jest nakładany na uzwojenie pierwotne transformatora. Niech napięcie rozwijane na każdym uzwojeniu wtórnym wynosi ð ?? '‰ ð ??' † 1 i ð ?? '‰ ð ??' † 2. Napięcie wyjściowe,$V_{0}$ przebiega przez punkty początkowe dwóch uzwojeń wtórnych.

Mathematically, napięcie wyjściowe, ð ?? '‰ 0 można zapisać jako

$$V_{0}= V_{S1}-V_{S2}$$

Nazywa się transformator obecny w powyższym obwodzie differential transformer, ponieważ wytwarza napięcie wyjściowe, które jest różnicą między $V_{S1}$ i $V_{S2}$.

• Jeśli rdzeń znajduje się w pozycji środkowej, to napięcie wyjściowe, $V_{0}$będzie równa zero. Ponieważ odpowiednie wielkości i fazy$V_{S1}$ i $V_{S2}$ Są takie same.

• Jeśli rdzeń nie znajduje się w pozycji środkowej, to napięcie wyjściowe, $V_{0}$będzie mieć pewną wielkość i fazę. Ponieważ odpowiednie wielkości i fazy$V_{S1}$ i $V_{S2}$ nie są równe.

Dlatego powinniśmy połączyć ciało, którego przemieszczenie ma być zmierzone, z centralnym rdzeniem. Tak więc za każdym razem, gdy ciało porusza się w linii prostej, zmienia się centralna pozycja rdzenia. Z tego powodu napięcie wyjściowe,$V_{0}$ również odpowiednio się zmienia.

W takim przypadku możemy znaleźć plik displacement mierząc napięcie wyjściowe, $V_{0}$. Wielkość i faza napięcia wyjściowego,$V_{0}$ reprezentuje odpowiednio przemieszczenie ciała i jego kierunek.

Pomiar przemieszczenia za pomocą przetwornika pojemnościowego

Plik circuit diagram przetwornika pojemnościowego, który służy do pomiaru przemieszczenia pokazano na poniższym rysunku.

Plik capacitor, który występuje w powyższym obwodzie ma dwie równoległe płytki. Wśród nich jedna płyta jest nieruchoma, a druga jest ruchoma. Z tego powodu odstępy między tymi dwoma płytami również będą się zmieniać. wartość pojemności zmienia się wraz ze zmianą odstępu między dwiema płytami kondensatora.

Dlatego powinniśmy połączyć ciało, którego displacementmierzy się do ruchomej płytki kondensatora. Tak więc za każdym razem, gdy korpus porusza się w linii prostej, odstępy między dwiema płytami kondensatora są różne. Z tego powodu zmienia się wartość pojemności.

Systemy używane do akwizycji danych są znane jako data acquisition systems. Te systemy akwizycji danych będą wykonywać zadania takie jak konwersja danych, przechowywanie danych, transmisja danych i ich przetwarzanie.

Systemy gromadzenia danych uwzględniają następujące kwestie analog signals.

• Sygnały analogowe, które są uzyskiwane z bezpośredniego pomiaru wielkości elektrycznych, takich jak napięcia DC i AC, prądy DC i AC, rezystancja itp.

• Sygnały analogowe, które są uzyskiwane z przetworników, takich jak LVDT, termopara itp.

Rodzaje systemów akwizycji danych

Systemy akwizycji danych można podzielić na następujące two types.

• Systemy akwizycji danych analogowych
• Cyfrowe systemy gromadzenia danych

Omówmy teraz kolejno te dwa typy systemów gromadzenia danych.

Systemy akwizycji danych analogowych

Systemy akwizycji danych, które mogą być obsługiwane za pomocą sygnałów analogowych, są znane jako analog data acquisition systems. Poniżej przedstawiono bloki analogowych systemów akwizycji danych.

• Transducer - Konwertuje wielkości fizyczne na sygnały elektryczne.

• Signal conditioner - Wykonuje funkcje takie jak wzmocnienie i wybór żądanej części sygnału.

• Display device - Wyświetla sygnały wejściowe w celu monitorowania.

• Graphic recording instruments - Można je wykorzystać do trwałego zapisu danych wejściowych.

• Magnetic tape instrumentation - Służy do pozyskiwania, przechowywania i odtwarzania danych wejściowych.

Cyfrowe systemy gromadzenia danych

Systemy gromadzenia danych, które mogą być obsługiwane za pomocą sygnałów cyfrowych, są znane jako digital data acquisition systems. Dlatego używają komponentów cyfrowych do przechowywania lub wyświetlania informacji.

Przede wszystkim następujące operations odbywają się w cyfrowym gromadzeniu danych.

• Akwizycja sygnałów analogowych
• Przetwarzanie sygnałów analogowych na sygnały cyfrowe lub dane cyfrowe
• Przetwarzanie sygnałów cyfrowych lub danych cyfrowych

Poniżej znajdują się bloki Digital data acquisition systems.

• Transducer - Konwertuje wielkości fizyczne na sygnały elektryczne.

• Signal conditioner - Wykonuje funkcje takie jak wzmocnienie i wybór żądanej części sygnału.

• Multiplexer- łączy jedno z wielu wejść do wyjścia. Działa więc jako konwerter równoległy do ​​szeregowego.

• Analog to Digital Converter - Konwertuje wejście analogowe na odpowiadające mu wyjście cyfrowe.

• Display device - Wyświetla dane w formacie cyfrowym.

• Digital Recorder - Służy do zapisywania danych w formacie cyfrowym.

Systemy gromadzenia danych są wykorzystywane w różnych zastosowaniach, takich jak biomedycyna i kosmonautyka. Możemy więc wybrać analogowe systemy akwizycji danych lub cyfrowe systemy akwizycji danych w zależności od wymagań.