Algorytmy klasyfikacji - drzewo decyzyjne

Wprowadzenie do drzewa decyzyjnego

Ogólnie rzecz biorąc, analiza drzewa decyzyjnego jest narzędziem do modelowania predykcyjnego, które można zastosować w wielu obszarach. Drzewa decyzyjne mogą być konstruowane za pomocą podejścia algorytmicznego, które może podzielić zbiór danych na różne sposoby w oparciu o różne warunki. Decyzje to najpotężniejsze algorytmy należące do kategorii algorytmów nadzorowanych.

Mogą być używane zarówno do zadań klasyfikacyjnych, jak i regresyjnych. Dwoma głównymi elementami drzewa są węzły decyzyjne, w których dane są dzielone i opuszcza, gdzie otrzymaliśmy wynik. Przykład drzewa binarnego służącego do przewidywania, czy dana osoba jest sprawna lub niezdolna, dostarczając różnych informacji, takich jak wiek, nawyki żywieniowe i nawyki związane z ćwiczeniami, podano poniżej

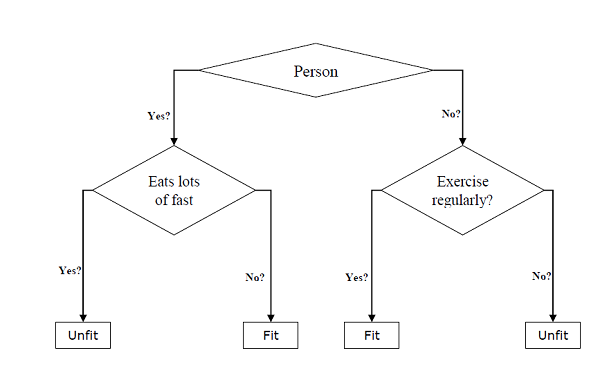
W powyższym drzewie decyzyjnym pytaniem są węzły decyzyjne, a ostateczne wyniki to liście. Mamy dwa rodzaje drzew decyzyjnych -

• Classification decision trees- W tego rodzaju drzewach decyzyjnych zmienna decyzyjna jest kategoryczna. Powyższe drzewo decyzyjne jest przykładem drzewa decyzyjnego klasyfikacyjnego.

• Regression decision trees - W tego rodzaju drzewach decyzyjnych zmienna decyzyjna jest ciągła.

Implementacja algorytmu drzewa decyzyjnego

Indeks Giniego

Jest to nazwa funkcji kosztu, która jest używana do oceny podziałów binarnych w zbiorze danych i współpracuje ze zmienną kategorialną „Sukces” lub „Niepowodzenie”.

Im wyższa wartość wskaźnika Giniego, tym wyższa jednorodność. Idealna wartość indeksu Giniego to 0, a najgorsza to 0,5 (dla zadania 2-klasowego). Indeks Giniego dla podziału można obliczyć za pomocą następujących kroków -

• Najpierw oblicz wskaźnik Giniego dla węzłów podrzędnych za pomocą wzoru p ^ 2 + q ^ 2, który jest sumą kwadratu prawdopodobieństwa sukcesu i porażki.

• Następnie oblicz wskaźnik Giniego dla podziału, używając ważonego wyniku Giniego każdego węzła tego podziału.

Algorytm drzewa klasyfikacji i regresji (CART) wykorzystuje metodę Giniego do generowania podziałów binarnych.

Podzielone tworzenie

Podział zasadniczo obejmuje atrybut w zbiorze danych i wartość. Możemy utworzyć podział w zbiorze danych za pomocą następujących trzech części -

• Part1: Calculating Gini Score - Omówiliśmy tę część w poprzedniej sekcji.

• Part2: Splitting a dataset- Można to zdefiniować jako rozdzielenie zbioru danych na dwie listy wierszy posiadających indeks atrybutu i wartość podziału tego atrybutu. Po uzyskaniu dwóch grup - prawej i lewej, ze zbioru danych możemy obliczyć wartość podziału za pomocą wyniku Giniego obliczonego w pierwszej części. Wartość podziału zadecyduje, w której grupie atrybut będzie się znajdował.

• Part3: Evaluating all splits- Następną częścią po znalezieniu wyniku Giniego i podzieleniu zestawu danych jest ocena wszystkich podziałów. W tym celu najpierw musimy sprawdzić każdą wartość związaną z każdym atrybutem jako kandydujący podział. Następnie musimy znaleźć najlepszy możliwy podział, oceniając koszt podziału. Najlepszy podział zostanie użyty jako węzeł w drzewie decyzyjnym.

Budowanie drzewa

Jak wiemy, drzewo ma węzeł główny i węzły końcowe. Po utworzeniu węzła głównego możemy zbudować drzewo, wykonując dwie części -

Część 1: Tworzenie węzła końcowego

Podczas tworzenia węzłów końcowych drzewa decyzyjnego ważną kwestią jest podjęcie decyzji, kiedy zatrzymać wzrost drzewa lub tworzenie kolejnych węzłów końcowych. Można to zrobić za pomocą dwóch kryteriów, mianowicie maksymalnej głębokości drzewa i minimalnych rekordów węzłów w następujący sposób:

• Maximum Tree Depth- Jak sama nazwa wskazuje, jest to maksymalna liczba węzłów w drzewie po węźle głównym. Musimy przestać dodawać węzły końcowe, gdy drzewo osiągnie maksymalną głębokość, tj. Gdy drzewo osiągnie maksymalną liczbę węzłów końcowych.

• Minimum Node Records- Można go zdefiniować jako minimalną liczbę wzorców treningowych, za które odpowiada dany węzeł. Musimy przestać dodawać węzły końcowe, gdy drzewo osiągnie te minimalne rekordy węzłów lub poniżej tego minimum.

Węzeł końcowy służy do sporządzania ostatecznej prognozy.

Część 2: Dzielenie rekurencyjne

Ponieważ zrozumieliśmy, kiedy tworzyć węzły końcowe, możemy teraz zacząć budować nasze drzewo. Dzielenie rekurencyjne to metoda budowania drzewa. W tej metodzie, po utworzeniu węzła, możemy utworzyć węzły potomne (węzły dodane do istniejącego węzła) rekurencyjnie na każdej grupie danych, generowane przez podzielenie zbioru danych, przez wielokrotne wywoływanie tej samej funkcji.

Prognoza

Po zbudowaniu drzewa decyzyjnego musimy go przewidzieć. Zasadniczo przewidywanie obejmuje nawigację po drzewie decyzyjnym za pomocą specjalnie dostarczonego wiersza danych.

Możemy dokonać prognozy za pomocą funkcji rekurencyjnej, tak jak to zrobiliśmy powyżej. Ta sama procedura przewidywania jest wywoływana ponownie z lewym lub podrzędnym prawym węzłem.

Założenia

Oto niektóre z założeń, jakie przyjmujemy podczas tworzenia drzewa decyzyjnego -

• Podczas przygotowywania drzew decyzyjnych zbiór uczący pełni rolę węzła głównego.

• Klasyfikator drzewa decyzyjnego preferuje kategoryczne wartości cech. W przypadku, gdy chcesz użyć wartości ciągłych, musisz je przeprowadzić dyskretnie przed zbudowaniem modelu.

• Na podstawie wartości atrybutu rekordy są rozprowadzane rekurencyjnie.

• Podejście statystyczne zostanie użyte do umieszczenia atrybutów w dowolnej pozycji węzła, tj. Jako węzeł główny lub węzeł wewnętrzny.

Implementacja w Pythonie

Przykład

W poniższym przykładzie zamierzamy zaimplementować klasyfikator drzewa decyzyjnego na Pima Indian Diabetes -

Najpierw zacznij od zaimportowania niezbędnych pakietów Pythona -

import pandas as pd
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split

Następnie pobierz zestaw danych tęczówki z łącza internetowego w następujący sposób -

col_names = ['pregnant', 'glucose', 'bp', 'skin', 'insulin', 'bmi', 'pedigree', 'age', 'label']
pima = pd.read_csv(r"C:\pima-indians-diabetes.csv", header=None, names=col_names)
pima.head()

pregnant    glucose  bp    skin  insulin  bmi   pedigree    age   label
0       6         148      72    35     0       33.6    0.627     50      1
1       1         85       66    29     0       26.6    0.351     31      0
2       8         183      64     0     0       23.3    0.672     32      1
3       1         89       66    23     94      28.1    0.167     21      0
4       0         137      40    35     168     43.1    2.288     33      1

Teraz podziel zbiór danych na funkcje i zmienną docelową w następujący sposób -

feature_cols = ['pregnant', 'insulin', 'bmi', 'age','glucose','bp','pedigree']
X = pima[feature_cols] # Features
y = pima.label # Target variable

Następnie podzielimy dane na podział na pociąg i test. Poniższy kod podzieli zbiór danych na 70% danych szkoleniowych i 30% danych testowych -

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=1)

Następnie wytrenuj model za pomocą klasy DecisionTreeClassifier sklearn w następujący sposób -

clf = DecisionTreeClassifier()
clf = clf.fit(X_train,y_train)

W końcu musimy przewidzieć. Można to zrobić za pomocą następującego skryptu -

y_pred = clf.predict(X_test)

Następnie możemy uzyskać wynik dokładności, macierz pomyłki i raport klasyfikacji w następujący sposób -

from sklearn.metrics import classification_report, confusion_matrix, accuracy_score
result = confusion_matrix(y_test, y_pred)
print("Confusion Matrix:")
print(result)
result1 = classification_report(y_test, y_pred)
print("Classification Report:",)
print (result1)
result2 = accuracy_score(y_test,y_pred)
print("Accuracy:",result2)

Wynik

Confusion Matrix:
[[116 30]
[ 46 39]]
Classification Report:
            precision   recall   f1-score    support
      0       0.72      0.79       0.75     146
      1       0.57      0.46       0.51     85
micro avg     0.67      0.67       0.67     231
macro avg     0.64      0.63       0.63     231
weighted avg  0.66      0.67       0.66     231

Accuracy: 0.670995670995671

Wizualizacja drzewa decyzyjnego

Powyższe drzewo decyzyjne można zwizualizować za pomocą następującego kodu -

from sklearn.tree import export_graphviz
from sklearn.externals.six import StringIO
from IPython.display import Image
import pydotplus

dot_data = StringIO()
export_graphviz(clf, out_file=dot_data,
      filled=True, rounded=True,
      special_characters=True,feature_names = feature_cols,class_names=['0','1'])
graph = pydotplus.graph_from_dot_data(dot_data.getvalue())
graph.write_png('Pima_diabetes_Tree.png')
Image(graph.create_png())