Energoelektronika - Choppers
Chopper wykorzystuje dużą prędkość do łączenia i odłączania obciążenia źródłowego. Stałe napięcie DC jest podawane okresowo do obciążenia źródła poprzez ciągłe wyzwalanie włącznika / wyłącznika zasilania. Okres czasu, przez który wyłącznik zasilania pozostaje włączony lub wyłączony, nazywany jest odpowiednio stanami WŁĄCZENIA i WYŁĄCZENIA przerywacza.
Rozdrabniacze są najczęściej stosowane w samochodach elektrycznych, konwersji energii wiatrowej i słonecznej oraz regulatorach silników prądu stałego.
Symbol Choppera
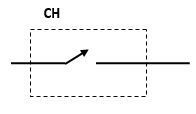
Klasyfikacja chopperów
W zależności od napięcia wyjściowego czopery są klasyfikowane jako -
- Step Up chopper (konwerter boost)
- Step Down Chopper (konwerter Buck)
- Step Up / Down Chopper (konwerter buck-boost)
Step Up Chopper
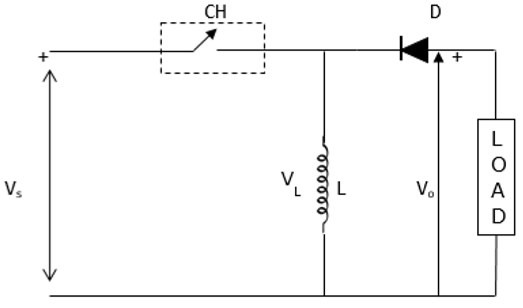
Średnie napięcie wyjściowe (V o ) w przerywaczu podwyższającym jest większe niż napięcie wejściowe (V s ). Poniższy rysunek przedstawia konfigurację przerywacza podwyższającego.
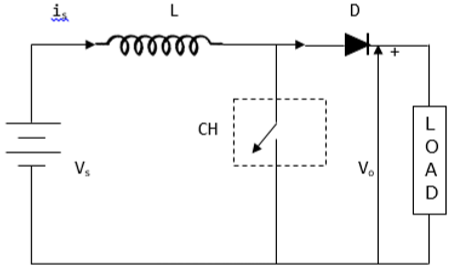
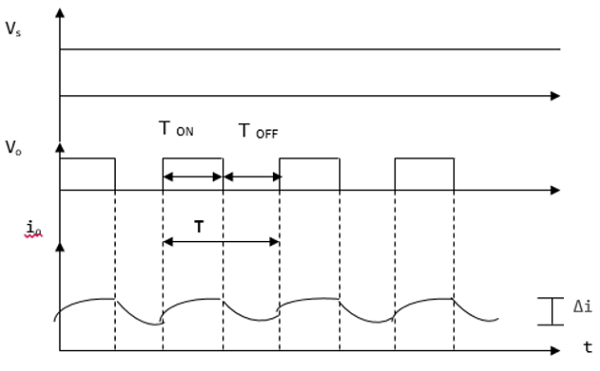
Przebiegi prądu i napięcia
V 0 (średnie napięcie wyjściowe) jest dodatnie, gdy przerywacz jest włączony i ujemne, gdy przerywacz jest wyłączony, jak pokazano na poniższym przebiegu.
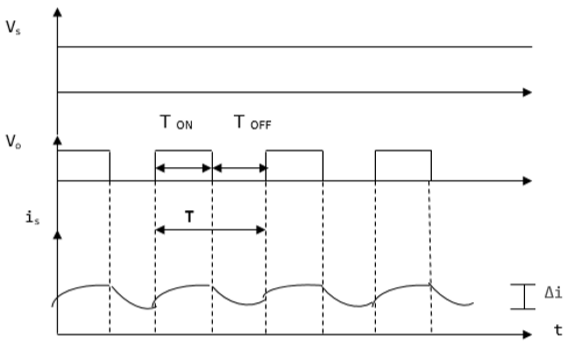
Gdzie
T ON - przedział czasu, w którym chopper jest włączony
T OFF - przedział czasu, w którym chopper jest wyłączony
V L - napięcie obciążenia
V s - napięcie źródła
T - Okres siekania = T ON + T OFF
V o jest określone przez -
$$ V_ {0} = \ frac {1} {T} \ int_ {0} ^ {T_ {ON}} V_ {S} dt $$Gdy przerywacz (CH) jest włączony, następuje zwarcie obciążenia, a tym samym wyjście napięcia na okres TONwynosi zero. Ponadto cewka indukcyjna jest w tym czasie ładowana. To daje V S = V L
$ L \ frac {di} {dt} = V_ {S}, $ $ \ frac {\ Delta i} {T_ {ON}} = \ frac {V_ {S}} {L} $
Stąd $ \ Delta i = \ frac {V_ {S}} {L} T_ {ON} $
Δi = jest prądem szczytowym cewki indukcyjnej. Gdy przerywacz (CH) jest WYŁĄCZONY, wyładowanie następuje przez cewkę indukcyjną L. Dlatego sumowanie V si V L jest podane w następujący sposób -
$ V_ {0} = V_ {S} + V_ {L}, \ quad V_ {L} = V_ {0} -V_ {S} $
Ale $ L \ frac {di} {dt} = V_ {0} -V_ {S} $
Zatem $ L \ frac {\ Delta i} {T_ {OFF}} = V_ {0} -V_ {S} $
To daje, $ \ Delta i = \ frac {V_ {0} -V_ {S}} {L} T_ {OFF} $
Zrównanie Δi od stanu ON do Δi od stanu OFF daje -
$ \ frac {V_ {S}} {L} T_ {ON} = \ frac {V_ {0} -V_ {S}} {L} T_ {OFF} $, $ V_ {S} \ left (T_ {ON } + T_ {OFF} \ right) = V_ {0} T_ {OFF} $
$ V_ {0} = \ frac {TV_ {S}} {T_ {OFF}} = \ frac {V_ {S}} {\ frac {\ left (T + T_ {ON} \ right)} {T}} $
Daje to średnie napięcie wyjściowe jako,
$$ V_ {0} = \ frac {V_ {S}} {1-D} $$Z powyższego równania wynika, że V o można zmieniać od V S do nieskończoności. Dowodzi, że napięcie wyjściowe zawsze będzie większe niż napięcie wejściowe, a tym samym podnosi lub zwiększa poziom napięcia.
Step Down Chopper
Jest to również znane jako konwerter złotówki. W tym przerywacza średnie napięcie wyjściowe V O jest mniejszy niż napięcie wejściowe V S . Gdy przerywacz jest włączony, V O = V S, a gdy przerywacz jest wyłączony, V O = 0
Gdy chopper jest włączony -
$ V_ {S} = \ left (V_ {L} + V_ {0} \ right), \ quad V_ {L} = V_ {S} -V_ {0}, \ quad L \ frac {di} {dt} = V_ {S} -V_ {0}, \ quad L \ frac {\ Delta i} {T_ {ON}} = V_ {s} + V_ {0} $
Zatem obciążenie prądem międzyszczytowym jest wyrażone wzorem,
$ \ Delta i = \ frac {V_ {s} -V_ {0}} {L} T_ {ON} $
Schemat obwodu
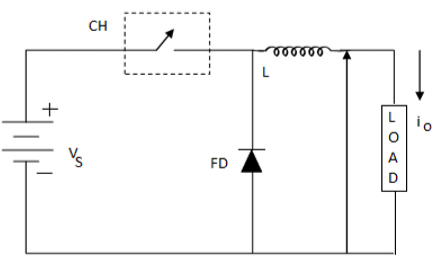
Gdzie FD to dioda wolnego koła.
Gdy przerywacz jest wyłączony, następuje odwrócenie polaryzacji i wyładowanie na cewce indukcyjnej. Prąd przepływa przez diodę wolnego koła i cewkę do obciążenia. To daje,
$$ L \ frac {di} {dt} = V_ {0} .................................. ...... \ left (i \ right) $$Przepisano jako - $ \ quad L \ frac {\ Delta i} {T_ {OFF}} = V_ {0} $
$$ \ Delta i = V_ {0} \ frac {T_ {OFF}} {L} ............................. ...... \ left (ii \ right) $$Równania (i) i (ii) dają;
$ \ frac {V_ {S} -V_ {0}} {L} T_ {ON} = \ frac {V_ {0}} {L} T_ {OFF} $
$ \ frac {V_ {S} -V_ {0}} {V_ {0}} = \ frac {T_ {OFF}} {T_ {ON}} $
$ \ frac {V_ {S}} {V_ {0}} = \ frac {T_ {ON} -T_ {OFF}} {T_ {ON}} $
Powyższe równanie daje;
$$ V_ {0} = \ frac {T_ {ON}} {T} V_ {S} = DV_ {S} $$Równanie (i) daje -
$ \ Delta i = \ frac {V_ {S} -DV_ {S}} {L} DT $, od $ D = \ frac {T_ {ON}} {T} $
$ = \ frac {V_ {S} - \ left (1-D \ right) D} {Lf} $
$ f = \ frac {1} {T} = $ częstotliwość siekania
Przebiegi prądu i napięcia
Przebiegi prądu i napięcia podano poniżej -
W przypadku przerywacza obniżającego napięcie wyjściowe jest zawsze mniejsze niż napięcie wejściowe. Pokazuje to poniższy przebieg.
Chopper w górę / w dół
Jest to również znane jako konwerter buck-boost. Umożliwia zwiększenie lub zmniejszenie poziomu wejściowego napięcia. Poniższy schemat przedstawia chopper buck-boost.
Gdy przerywacz jest włączony, cewka L zostaje naładowana przez źródło zasilania V s . W związku z tym, V y = v L .
$$ L \ frac {di} {dt} = V_ {S} $$ \ Delta i = \ frac {V_ {S}} {L} T_ {ON} = \ frac {V_ {S}} {L } T \ frac {T_ {ON}} {T} = \ frac {DV_ {S}} {Lf} $$Ponieważ -
$ D = \ frac {T_ {ON}} {T} $ i $ f = \ frac {1} {T} ....................... ....................... \ left (iii \ right) $
Gdy przerywacz jest wyłączony, polaryzacja cewki zmienia się, co powoduje jej rozładowanie przez diodę i obciążenie.
W związku z tym,
$$ V_ {0} = - V_ {L} $$ $$ L \ frac {di} {dt} = - V_ {0} $$$ L \ frac {\ Delta i} {T_ {OFF}} = - V_ {0} $, więc $ \ Delta i = - \ frac {V_ {0}} {L} T_ {OFF} ..... ........................... \ left (iv \ right) $
Obliczanie równania (iii) i (iv) daje -
$ \ frac {DV_ {S}} {Lf} = - \ frac {V_ {0}} {L} T_ {OFF} $, $ DV_ {S} = - DV_ {S} = - V_ {0} T_ { OFF} f $
$ DV_ {S} = - V_ {0} \ frac {T-T_ {ON}} {T} = - V_ {0} \ left (1- \ frac {T_ {ON}} {T} \ right) $ , $ V_ {0} = - \ frac {DV_ {S}} {1-D} $
Ponieważ $ D = \ frac {T_ {ON}} {T} = \ frac {T-T_ {OFF}} {1-D} $
To daje,
$ V_ {0} = \ frac {DV_ {S}} {1-D} $
D może zmieniać się od 0 do 1. Kiedy, D = 0; V O = 0
Gdy D = 0,5, V O = V S
Kiedy D = 1, V O = ∞.
Stąd w przedziale 0 ≤ D ≤ 0,5 napięcie wyjściowe zmienia się w zakresie 0 ≤ V O <V S i otrzymujemy obniżanie lub operację Buck. Natomiast w przedziale 0,5 ≤ D ≤ 1 napięcie wyjściowe zmienia się w zakresie V S ≤ V O ≤ ∞ i otrzymujemy działanie podwyższające lub podwyższające.