PyTorch - regresja liniowa

W tym rozdziale skupimy się na podstawowym przykładzie implementacji regresji liniowej przy użyciu TensorFlow. Regresja logistyczna lub regresja liniowa to nadzorowane podejście uczenia maszynowego do klasyfikacji dyskretnych kategorii porządku. Naszym celem w tym rozdziale jest zbudowanie modelu, za pomocą którego użytkownik może przewidzieć związek między zmiennymi predykcyjnymi a jedną lub większą liczbą zmiennych niezależnych.

Zależność między tymi dwiema zmiennymi jest uważana za liniową, tj. Jeśli y jest zmienną zależną, a x jest uważane za zmienną niezależną, wówczas zależność regresji liniowej dwóch zmiennych będzie wyglądać jak równanie, o którym mowa poniżej -

Y = Ax+b

Następnie zaprojektujemy algorytm regresji liniowej, który pozwoli nam zrozumieć dwa ważne pojęcia podane poniżej -

• Funkcja kosztu
• Algorytmy zejścia gradientowego

Schematyczne przedstawienie regresji liniowej jest wymienione poniżej

Interpretacja wyniku

$$ Y = topór + b $$

• Wartość a to nachylenie.

• Wartość b jest y − intercept.

• r jest correlation coefficient.

• r² jest correlation coefficient.

Graficzny widok równania regresji liniowej przedstawiono poniżej -

Poniższe kroki służą do implementacji regresji liniowej za pomocą PyTorch -

Krok 1

Zaimportuj niezbędne pakiety do tworzenia regresji liniowej w PyTorch przy użyciu poniższego kodu -

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
import seaborn as sns
import pandas as pd
%matplotlib inline

sns.set_style(style = 'whitegrid')
plt.rcParams["patch.force_edgecolor"] = True

Krok 2

Utwórz pojedynczy zestaw uczący z dostępnym zestawem danych, jak pokazano poniżej -

m = 2 # slope
c = 3 # interceptm = 2 # slope
c = 3 # intercept
x = np.random.rand(256)

noise = np.random.randn(256) / 4

y = x * m + c + noise

df = pd.DataFrame()
df['x'] = x
df['y'] = y

sns.lmplot(x ='x', y ='y', data = df)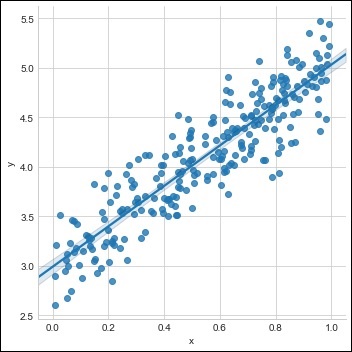

Krok 3

Zaimplementuj regresję liniową za pomocą bibliotek PyTorch, jak wspomniano poniżej -

import torch
import torch.nn as nn
from torch.autograd import Variable
x_train = x.reshape(-1, 1).astype('float32')
y_train = y.reshape(-1, 1).astype('float32')

class LinearRegressionModel(nn.Module):
   def __init__(self, input_dim, output_dim):
      super(LinearRegressionModel, self).__init__()
      self.linear = nn.Linear(input_dim, output_dim)

   def forward(self, x):
      out = self.linear(x)
      return out
input_dim = x_train.shape[1]
output_dim = y_train.shape[1]
input_dim, output_dim(1, 1)
model = LinearRegressionModel(input_dim, output_dim)
criterion = nn.MSELoss()
[w, b] = model.parameters()

def get_param_values():
   return w.data[0][0], b.data[0]

def plot_current_fit(title = ""):
plt.figure(figsize = (12,4))
plt.title(title)
plt.scatter(x, y, s = 8)
w1 = w.data[0][0]
b1 = b.data[0]
x1 = np.array([0., 1.])
y1 = x1 * w1 + b1
plt.plot(x1, y1, 'r', label = 'Current Fit ({:.3f}, {:.3f})'.format(w1, b1))
plt.xlabel('x (input)')
plt.ylabel('y (target)')
plt.legend()
plt.show()
plot_current_fit('Before training')

Wygenerowany wykres przedstawia się następująco -