PyTorch - Szybki przewodnik

PyTorch jest zdefiniowany jako biblioteka uczenia maszynowego typu open source dla języka Python. Jest używany do zastosowań, takich jak przetwarzanie języka naturalnego. Jest początkowo opracowany przez grupę badawczą zajmującą się sztuczną inteligencją Facebooka i oprogramowanie Pyro firmy Uber do programowania probabilistycznego, które jest na nim zbudowane.

Pierwotnie PyTorch został opracowany przez Hugh Perkinsa jako opakowanie Pythona dla LusJIT opartego na frameworku Torch. Istnieją dwa warianty PyTorch.

PyTorch przeprojektowuje i implementuje Torch w Pythonie, współdzieląc te same podstawowe biblioteki C dla kodu zaplecza. Programiści PyTorch dostroili ten kod zaplecza, aby wydajnie uruchamiać Pythona. Zachowali także akcelerację sprzętową opartą na GPU, a także funkcje rozszerzalności, które stworzyły Torch oparty na Lua.

funkcje

Poniżej wymieniono główne cechy PyTorch -

Easy Interface- PyTorch oferuje łatwe w użyciu API; dlatego jest uważany za bardzo prosty w obsłudze i działa w Pythonie. Wykonanie kodu w tym frameworku jest dość łatwe.

Python usage- Ta biblioteka jest uważana za Pythonic, która płynnie integruje się ze stosem nauki o danych Python. W ten sposób może wykorzystać wszystkie usługi i funkcje oferowane przez środowisko Python.

Computational graphs- PyTorch zapewnia doskonałą platformę, która oferuje dynamiczne wykresy obliczeniowe. W ten sposób użytkownik może je zmieniać w trakcie działania. Jest to bardzo przydatne, gdy programista nie ma pojęcia, ile pamięci jest potrzebne do utworzenia modelu sieci neuronowej.

PyTorch jest znany z trzech poziomów abstrakcji, jak podano poniżej -

• Tensor - imperatywna tablica n-wymiarowa działająca na GPU.

• Zmienna - węzeł w grafie obliczeniowym. To przechowuje dane i gradient.

• Moduł - warstwa sieci neuronowej, która będzie przechowywać wagi stanu lub możliwe do nauczenia się.

Zalety PyTorch

Oto zalety PyTorch -

• Łatwo jest debugować i zrozumieć kod.

• Zawiera wiele warstw, takich jak Torch.

• Zawiera wiele funkcji utraty.

• Można to uznać za rozszerzenie NumPy na GPU.

• Umożliwia budowanie sieci, których struktura zależy od samych obliczeń.

TensorFlow kontra PyTorch

Poniżej przyjrzymy się głównym różnicom między TensorFlow i PyTorch -

PyTorch	TensorFlow
PyTorch jest ściśle powiązany z platformą Torch opartą na lua, która jest aktywnie wykorzystywana na Facebooku.	TensorFlow jest rozwijany przez Google Brain i aktywnie używany w Google.
PyTorch jest stosunkowo nowy w porównaniu do innych konkurencyjnych technologii.	TensorFlow nie jest nowy i wielu badaczy i profesjonalistów z branży uważa go za gotowe do użycia.
PyTorch zawiera wszystko w sposób imperatywny i dynamiczny.	TensorFlow zawiera statyczne i dynamiczne wykresy jako kombinację.
Wykres obliczeniowy w PyTorch jest definiowany w czasie wykonywania.	TensorFlow nie zawiera żadnych opcji wykonawczych.
PyTorch obejmuje wdrożenia przeznaczone dla platform mobilnych i wbudowanych.	TensorFlow działa lepiej w przypadku struktur osadzonych.

PyTorch to popularna platforma uczenia głębokiego. W tym samouczku jako nasz system operacyjny uważamy „Windows 10”. Kroki udanej konfiguracji środowiska są następujące:

Krok 1

Poniższy link zawiera listę pakietów, która zawiera odpowiednie pakiety dla PyTorch.

https://drive.google.com/drive/folders/0B-X0-FlSGfCYdTNldW02UGl4MXM

Wszystko, co musisz zrobić, to pobrać odpowiednie pakiety i zainstalować je, jak pokazano na poniższych zrzutach ekranu -

Krok 2

Obejmuje weryfikację instalacji frameworka PyTorch przy użyciu Anaconda Framework.

Następujące polecenie służy do weryfikacji tego samego -

conda list

„Lista Conda” pokazuje listę zainstalowanych frameworków.

Podświetlona część pokazuje, że PyTorch został pomyślnie zainstalowany w naszym systemie.

Matematyka jest niezbędna w każdym algorytmie uczenia maszynowego i obejmuje różne podstawowe pojęcia matematyczne, aby uzyskać odpowiedni algorytm zaprojektowany w określony sposób.

Znaczenie tematów matematycznych dla uczenia maszynowego i nauki o danych jest wymienione poniżej -

Teraz skupmy się na głównych koncepcjach matematycznych uczenia maszynowego, które są ważne z punktu widzenia przetwarzania języka naturalnego -

Wektory

Za wektor uważa się tablicę liczb, która jest ciągła lub dyskretna, a przestrzeń, która składa się z wektorów, nazywana jest przestrzenią wektorową. Wymiary przestrzenne wektorów mogą być skończone lub nieskończone, ale zaobserwowano, że problemy z uczeniem maszynowym i nauką o danych dotyczą wektorów o stałej długości.

Reprezentacja wektorowa jest wyświetlana, jak wspomniano poniżej -

temp = torch.FloatTensor([23,24,24.5,26,27.2,23.0])
temp.size()
Output - torch.Size([6])

W uczeniu maszynowym mamy do czynienia z wielowymiarowymi danymi. Zatem wektory stają się bardzo istotne i są traktowane jako cechy wejściowe dla każdego stwierdzenia problemu z prognozowaniem.

Skalary

Skalary mają zerowe wymiary zawierające tylko jedną wartość. Jeśli chodzi o PyTorch, to nie zawiera specjalnego tensora o zerowych wymiarach; stąd deklaracja będzie następująca -

x = torch.rand(10)
x.size()
Output - torch.Size([10])

Matryce

Większość danych strukturalnych jest zwykle reprezentowana w postaci tabel lub określonej macierzy. Użyjemy zestawu danych o nazwie Boston House Prices, który jest łatwo dostępny w bibliotece uczenia maszynowego Python scikit-Learn.

boston_tensor = torch.from_numpy(boston.data)
boston_tensor.size()
Output: torch.Size([506, 13])
boston_tensor[:2]
Output:
Columns 0 to 7
0.0063 18.0000 2.3100 0.0000 0.5380 6.5750 65.2000 4.0900
0.0273 0.0000 7.0700 0.0000 0.4690 6.4210 78.9000 4.9671
Columns 8 to 12
1.0000 296.0000 15.3000 396.9000 4.9800
2.0000 242.0000 17.8000 396.9000 9.1400

Podstawowa zasada działania sieci neuronowej obejmuje zbiór podstawowych elementów, czyli sztuczny neuron lub perceptron. Zawiera kilka podstawowych wejść, takich jak x1, x2… .. xn, które generują wyjście binarne, jeśli suma jest większa niż potencjał aktywacji.

Schematyczne przedstawienie neuronu próbki jest wymienione poniżej -

Wygenerowane wyjście można uznać za sumę ważoną z potencjałem aktywacji lub odchyleniem.

$$ Wyjście = \ sum_jw_jx_j + Odchylenie $$

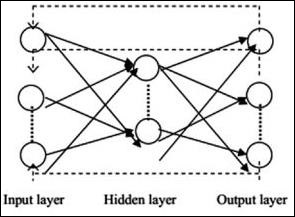
Poniżej opisano typową architekturę sieci neuronowej -

Warstwy między wejściami i wyjściami są nazywane warstwami ukrytymi, a gęstość i typ połączeń między warstwami to konfiguracja. Na przykład, w pełni połączona konfiguracja ma wszystkie neurony warstwy L połączone z neuronami L + 1. Aby uzyskać bardziej wyrazistą lokalizację, do następnej warstwy możemy podłączyć tylko lokalne sąsiedztwo, powiedzmy dziewięć neuronów. Rysunek 1-9 przedstawia dwie ukryte warstwy z gęstymi połączeniami.

Różne typy sieci neuronowych są następujące -

Sieci neuronowe z wyprzedzeniem

Sieci neuronowe typu feedforward obejmują podstawowe jednostki rodziny sieci neuronowych. Ruch danych w tego typu sieci neuronowej odbywa się z warstwy wejściowej do warstwy wyjściowej, poprzez obecne warstwy ukryte. Wyjście jednej warstwy służy jako warstwa wejściowa z ograniczeniami dotyczącymi wszelkiego rodzaju pętli w architekturze sieci.

Powtarzające się sieci neuronowe

Powtarzające się sieci neuronowe mają miejsce, gdy wzór danych zmienia się konsekwentnie w okresie. W RNN ta sama warstwa jest stosowana do akceptowania parametrów wejściowych i wyświetlania parametrów wyjściowych w określonej sieci neuronowej.

Sieci neuronowe można budować za pomocą pakietu torch.nn.

Jest to prosta sieć ze sprzężeniem zwrotnym. Pobiera dane wejściowe, przepuszcza je przez kilka warstw jedna po drugiej, a na końcu podaje dane wyjściowe.

Z pomocą PyTorch możemy wykonać następujące kroki dla typowej procedury szkoleniowej dla sieci neuronowej -

• Zdefiniuj sieć neuronową, która ma pewne parametry (lub wagi), których można się nauczyć.
• Iteruj po zbiorze danych wejściowych.
• Przetwarzanie danych przez sieć.
• Oblicz stratę (jak daleko jest do poprawności wyniku).
• Propaguj gradienty z powrotem do parametrów sieci.
• Zaktualizuj wagi sieci, zwykle za pomocą prostej aktualizacji, jak podano poniżej

rule: weight = weight -learning_rate * gradient

Sztuczna inteligencja zyskuje obecnie na popularności. Uczenie maszynowe i uczenie głębokie to sztuczna inteligencja. Wspomniany poniżej diagram Venna wyjaśnia związek między uczeniem maszynowym a uczeniem głębokim.

Nauczanie maszynowe

Uczenie maszynowe to sztuka naukowa, która pozwala komputerom działać zgodnie z zaprojektowanymi i zaprogramowanymi algorytmami. Wielu badaczy uważa, że ​​uczenie maszynowe to najlepszy sposób na osiągnięcie postępu w kierunku sztucznej inteligencji na poziomie ludzkim. Obejmuje różne rodzaje wzorów, takich jak -

• Nadzorowany wzorzec uczenia się
• Nienadzorowany wzorzec uczenia się

Głęboka nauka

Głębokie uczenie się to poddziedzina uczenia maszynowego, w której algorytmy są inspirowane strukturą i funkcją mózgu zwanymi sztucznymi sieciami neuronowymi.

Głębokie uczenie zyskało duże znaczenie dzięki nadzorowanemu uczeniu się lub uczeniu się na podstawie oznaczonych danych i algorytmów. Każdy algorytm w głębokim uczeniu przechodzi przez ten sam proces. Obejmuje hierarchię nieliniowej transformacji danych wejściowych i wykorzystuje do tworzenia modelu statystycznego jako wyniku.

Proces uczenia maszynowego jest definiowany za pomocą następujących kroków -

• Identyfikuje odpowiednie zbiory danych i przygotowuje je do analizy.
• Wybiera typ algorytmu do użycia.
• Buduje model analityczny w oparciu o zastosowany algorytm.
• Trenuje model na testowych zestawach danych i koryguje go w razie potrzeby.
• Uruchamia model w celu wygenerowania wyników testów.

W tym rozdziale omówimy główną różnicę między koncepcjami uczenia maszynowego i głębokiego.

Ilość danych

Uczenie maszynowe działa z różnymi ilościami danych i jest używane głównie w przypadku niewielkich ilości danych. Z drugiej strony, uczenie głębokie działa skutecznie, jeśli ilość danych gwałtownie rośnie. Poniższy diagram przedstawia działanie uczenia maszynowego i uczenia głębokiego w odniesieniu do ilości danych -

Zależności sprzętowe

Algorytmy głębokiego uczenia są zaprojektowane tak, aby w dużym stopniu polegały na maszynach wysokiej klasy, w przeciwieństwie do tradycyjnych algorytmów uczenia maszynowego. Algorytmy głębokiego uczenia wykonują dużą liczbę operacji mnożenia macierzy, co wymaga ogromnego wsparcia sprzętowego.

Inżynieria funkcji

Inżynieria cech to proces polegający na umieszczaniu wiedzy dziedzinowej w określonych funkcjach w celu zmniejszenia złożoności danych i stworzenia wzorców widocznych dla algorytmów uczących się.

Na przykład tradycyjne wzorce uczenia maszynowego koncentrują się na pikselach i innych atrybutach potrzebnych w procesie inżynierii funkcji. Algorytmy uczenia głębokiego koncentrują się na funkcjach wysokiego poziomu z danych. Zmniejsza to zadanie tworzenia nowego ekstraktora funkcji dla każdego nowego problemu.

PyTorch zawiera specjalną funkcję tworzenia i wdrażania sieci neuronowych. W tym rozdziale utworzymy prostą sieć neuronową z jedną ukrytą warstwą tworzącą pojedynczą jednostkę wyjściową.

Wykonamy następujące kroki, aby zaimplementować pierwszą sieć neuronową za pomocą PyTorch -

Krok 1

Najpierw musimy zaimportować bibliotekę PyTorch za pomocą poniższego polecenia -

import torch 
import torch.nn as nn

Krok 2

Zdefiniuj wszystkie warstwy i rozmiar wsadu, aby rozpocząć wykonywanie sieci neuronowej, jak pokazano poniżej -

# Defining input size, hidden layer size, output size and batch size respectively
n_in, n_h, n_out, batch_size = 10, 5, 1, 10

Krok 3

Ponieważ sieć neuronowa zawiera kombinację danych wejściowych w celu uzyskania odpowiednich danych wyjściowych, będziemy postępować zgodnie z tą samą procedurą, którą podano poniżej -

# Create dummy input and target tensors (data)
x = torch.randn(batch_size, n_in)
y = torch.tensor([[1.0], [0.0], [0.0], 
[1.0], [1.0], [1.0], [0.0], [0.0], [1.0], [1.0]])

Krok 4

Utwórz model sekwencyjny za pomocą wbudowanych funkcji. Korzystając z poniższych linii kodu, utwórz model sekwencyjny -

# Create a model
model = nn.Sequential(nn.Linear(n_in, n_h),
   nn.ReLU(),
   nn.Linear(n_h, n_out),
   nn.Sigmoid())

Krok 5

Skonstruuj funkcję strat za pomocą optymalizatora Gradient Descent, jak pokazano poniżej -

Construct the loss function
criterion = torch.nn.MSELoss()
# Construct the optimizer (Stochastic Gradient Descent in this case)
optimizer = torch.optim.SGD(model.parameters(), lr = 0.01)

Krok 6

Zaimplementuj model gradientu z pętlą iteracyjną z podanymi wierszami kodu -

# Gradient Descent
for epoch in range(50):
   # Forward pass: Compute predicted y by passing x to the model
   y_pred = model(x)

   # Compute and print loss
   loss = criterion(y_pred, y)
   print('epoch: ', epoch,' loss: ', loss.item())

   # Zero gradients, perform a backward pass, and update the weights.
   optimizer.zero_grad()

   # perform a backward pass (backpropagation)
   loss.backward()

   # Update the parameters
   optimizer.step()

Krok 7

Wygenerowane dane wyjściowe są następujące -

epoch: 0 loss: 0.2545787990093231
epoch: 1 loss: 0.2545052170753479
epoch: 2 loss: 0.254431813955307
epoch: 3 loss: 0.25435858964920044
epoch: 4 loss: 0.2542854845523834
epoch: 5 loss: 0.25421255826950073
epoch: 6 loss: 0.25413978099823
epoch: 7 loss: 0.25406715273857117
epoch: 8 loss: 0.2539947032928467
epoch: 9 loss: 0.25392240285873413
epoch: 10 loss: 0.25385022163391113
epoch: 11 loss: 0.25377824902534485
epoch: 12 loss: 0.2537063956260681
epoch: 13 loss: 0.2536346912384033
epoch: 14 loss: 0.25356316566467285
epoch: 15 loss: 0.25349172949790955
epoch: 16 loss: 0.25342053174972534
epoch: 17 loss: 0.2533493936061859
epoch: 18 loss: 0.2532784342765808
epoch: 19 loss: 0.25320762395858765
epoch: 20 loss: 0.2531369626522064
epoch: 21 loss: 0.25306645035743713
epoch: 22 loss: 0.252996027469635
epoch: 23 loss: 0.2529257833957672
epoch: 24 loss: 0.25285571813583374
epoch: 25 loss: 0.25278574228286743
epoch: 26 loss: 0.25271597504615784
epoch: 27 loss: 0.25264623761177063
epoch: 28 loss: 0.25257670879364014
epoch: 29 loss: 0.2525072991847992
epoch: 30 loss: 0.2524380087852478
epoch: 31 loss: 0.2523689270019531
epoch: 32 loss: 0.25229987502098083
epoch: 33 loss: 0.25223103165626526
epoch: 34 loss: 0.25216227769851685
epoch: 35 loss: 0.252093642950058
epoch: 36 loss: 0.25202515721321106
epoch: 37 loss: 0.2519568204879761
epoch: 38 loss: 0.251888632774353
epoch: 39 loss: 0.25182053446769714
epoch: 40 loss: 0.2517525553703308
epoch: 41 loss: 0.2516847252845764
epoch: 42 loss: 0.2516169846057892
epoch: 43 loss: 0.2515493929386139
epoch: 44 loss: 0.25148195028305054
epoch: 45 loss: 0.25141456723213196
epoch: 46 loss: 0.2513473629951477
epoch: 47 loss: 0.2512802183628082
epoch: 48 loss: 0.2512132525444031
epoch: 49 loss: 0.2511464059352875

Trenowanie algorytmu głębokiego uczenia obejmuje następujące kroki -

• Tworzenie potoku danych
• Budowanie architektury sieciowej
• Ocena architektury za pomocą funkcji straty
• Optymalizacja architektury sieci waży przy użyciu algorytmu optymalizacji

Trenowanie określonego algorytmu głębokiego uczenia jest dokładnym wymogiem konwersji sieci neuronowej na bloki funkcjonalne, jak pokazano poniżej -

W odniesieniu do powyższego diagramu, każdy algorytm głębokiego uczenia polega na pobieraniu danych wejściowych, budowaniu odpowiedniej architektury, która zawiera kilka osadzonych w nich warstw.

Jeśli przyjrzymy się powyższemu diagramowi, dokładność jest oceniana za pomocą funkcji strat w odniesieniu do optymalizacji wag sieci neuronowej.

W tym rozdziale omówimy niektóre z najczęściej używanych terminów w PyTorch.

PyTorch NumPy

Tensor PyTorch jest identyczny z tablicą NumPy. Tensor jest tablicą n-wymiarową iw odniesieniu do PyTorch zapewnia wiele funkcji do działania na tych tensorach.

Tensory PyTorch zwykle wykorzystują GPU do przyspieszenia swoich obliczeń numerycznych. Te tensory, które są tworzone w PyTorch, mogą być używane do dopasowania sieci dwuwarstwowej do losowych danych. Użytkownik może ręcznie zaimplementować przejścia do przodu i do tyłu przez sieć.

Zmienne i Autograd

Podczas korzystania z autograd przekazanie do przodu twojej sieci zdefiniuje plik computational graph - węzły na wykresie będą tensorami, a krawędzie będą funkcjami, które generują tensory wyjściowe z tensorów wejściowych.

PyTorch Tensory można tworzyć jako obiekty zmienne, w których zmienna reprezentuje węzeł na wykresie obliczeniowym.

Dynamiczne wykresy

Wykresy statyczne są fajne, ponieważ użytkownik może z góry zoptymalizować wykres. Jeśli programiści ponownie używają tego samego wykresu w kółko, wówczas ta potencjalnie kosztowna wstępna optymalizacja może zostać utrzymana, ponieważ ten sam wykres jest powtarzany w kółko.

Główna różnica między nimi polega na tym, że wykresy obliczeniowe Tensor Flow są statyczne, a PyTorch wykorzystuje dynamiczne wykresy obliczeniowe.

Pakiet Optim

Pakiet Optim w PyTorch abstrahuje od idei algorytmu optymalizacji, który jest implementowany na wiele sposobów i dostarcza ilustracji powszechnie używanych algorytmów optymalizacji. Można to wywołać w instrukcji importu.

Wieloprocesowość

Wieloprocesorowość obsługuje te same operacje, więc wszystkie tensory działają na wielu procesorach. Kolejka będzie miała swoje dane przeniesione do pamięci współdzielonej i wyśle ​​tylko dojście do innego procesu.

PyTorch zawiera pakiet zwany torchvision, który służy do ładowania i przygotowywania zestawu danych. Zawiera dwie podstawowe funkcje, a mianowicie Dataset i DataLoader, które pomagają w transformacji i ładowaniu zestawu danych.

Zestaw danych

Zestaw danych służy do odczytywania i przekształcania punktu danych z danego zestawu danych. Podstawowa składnia do zaimplementowania jest wymieniona poniżej -

trainset = torchvision.datasets.CIFAR10(root = './data', train = True,
   download = True, transform = transform)

DataLoader służy do odtwarzania losowego i wsadowego danych. Może być używany do ładowania danych równolegle z pracownikami wieloprocesorowymi.

trainloader = torch.utils.data.DataLoader(trainset, batch_size = 4,
   shuffle = True, num_workers = 2)

Przykład: ładowanie pliku CSV

Używamy pakietu Python Panda do załadowania pliku csv. Oryginalny plik ma następujący format: (nazwa obrazu, 68 punktów orientacyjnych - każdy punkt orientacyjny ma współrzędne ax, y).

landmarks_frame = pd.read_csv('faces/face_landmarks.csv')

n = 65
img_name = landmarks_frame.iloc[n, 0]
landmarks = landmarks_frame.iloc[n, 1:].as_matrix()
landmarks = landmarks.astype('float').reshape(-1, 2)

W tym rozdziale skupimy się na podstawowym przykładzie implementacji regresji liniowej przy użyciu TensorFlow. Regresja logistyczna lub regresja liniowa to nadzorowane podejście uczenia maszynowego do klasyfikacji dyskretnych kategorii porządku. Naszym celem w tym rozdziale jest zbudowanie modelu, za pomocą którego użytkownik może przewidzieć związek między zmiennymi predykcyjnymi a jedną lub większą liczbą zmiennych niezależnych.

Zależność między tymi dwiema zmiennymi jest uważana za liniową, tj. Jeśli y jest zmienną zależną, a x jest uważane za zmienną niezależną, wówczas zależność regresji liniowej dwóch zmiennych będzie wyglądać jak równanie, o którym mowa poniżej -

Y = Ax+b

Następnie zaprojektujemy algorytm regresji liniowej, który pozwoli nam zrozumieć dwa ważne pojęcia podane poniżej -

• Funkcja kosztu
• Algorytmy zejścia gradientowego

Schematyczne przedstawienie regresji liniowej jest wymienione poniżej

Interpretacja wyniku

$$ Y = topór + b $$

• Wartość a to nachylenie.

• Wartość b jest y − intercept.

• r jest correlation coefficient.

• r² jest correlation coefficient.

Graficzny widok równania regresji liniowej przedstawiono poniżej -

Poniższe kroki służą do implementacji regresji liniowej za pomocą PyTorch -

Krok 1

Zaimportuj niezbędne pakiety do tworzenia regresji liniowej w PyTorch przy użyciu poniższego kodu -

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
import seaborn as sns
import pandas as pd
%matplotlib inline

sns.set_style(style = 'whitegrid')
plt.rcParams["patch.force_edgecolor"] = True

Krok 2

Utwórz pojedynczy zestaw uczący z dostępnym zestawem danych, jak pokazano poniżej -

m = 2 # slope
c = 3 # interceptm = 2 # slope
c = 3 # intercept
x = np.random.rand(256)

noise = np.random.randn(256) / 4

y = x * m + c + noise

df = pd.DataFrame()
df['x'] = x
df['y'] = y

sns.lmplot(x ='x', y ='y', data = df)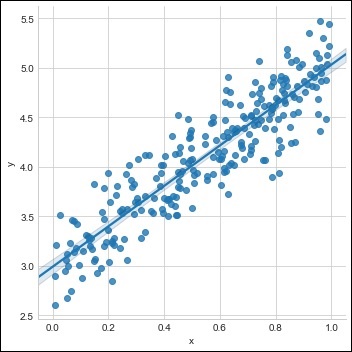

Krok 3

Zaimplementuj regresję liniową za pomocą bibliotek PyTorch, jak wspomniano poniżej -

import torch
import torch.nn as nn
from torch.autograd import Variable
x_train = x.reshape(-1, 1).astype('float32')
y_train = y.reshape(-1, 1).astype('float32')

class LinearRegressionModel(nn.Module):
   def __init__(self, input_dim, output_dim):
      super(LinearRegressionModel, self).__init__()
      self.linear = nn.Linear(input_dim, output_dim)

   def forward(self, x):
      out = self.linear(x)
      return out
input_dim = x_train.shape[1]
output_dim = y_train.shape[1]
input_dim, output_dim(1, 1)
model = LinearRegressionModel(input_dim, output_dim)
criterion = nn.MSELoss()
[w, b] = model.parameters()

def get_param_values():
   return w.data[0][0], b.data[0]

def plot_current_fit(title = ""):
plt.figure(figsize = (12,4))
plt.title(title)
plt.scatter(x, y, s = 8)
w1 = w.data[0][0]
b1 = b.data[0]
x1 = np.array([0., 1.])
y1 = x1 * w1 + b1
plt.plot(x1, y1, 'r', label = 'Current Fit ({:.3f}, {:.3f})'.format(w1, b1))
plt.xlabel('x (input)')
plt.ylabel('y (target)')
plt.legend()
plt.show()
plot_current_fit('Before training')

Wygenerowany wykres przedstawia się następująco -

Głębokie uczenie się jest działem uczenia maszynowego i jest uważane za kluczowy krok podjęty przez naukowców w ostatnich dziesięcioleciach. Przykłady implementacji uczenia głębokiego obejmują aplikacje takie jak rozpoznawanie obrazu i rozpoznawanie mowy.

Poniżej podano dwa ważne typy głębokich sieci neuronowych -

• Konwolucyjne sieci neuronowe
• Powtarzające się sieci neuronowe.

W tym rozdziale skupimy się na pierwszym typie, tj. Konwolucyjnych sieciach neuronowych (CNN).

Konwolucyjne sieci neuronowe

Konwolucyjne sieci neuronowe są przeznaczone do przetwarzania danych przez wiele warstw macierzy. Ten typ sieci neuronowych jest używany w aplikacjach takich jak rozpoznawanie obrazu lub rozpoznawanie twarzy.

Podstawowa różnica między CNN a jakąkolwiek inną zwykłą siecią neuronową polega na tym, że CNN przyjmuje dane wejściowe jako dwuwymiarowa tablica i działa bezpośrednio na obrazach, zamiast skupiać się na ekstrakcji cech, na której koncentrują się inne sieci neuronowe.

Dominujące podejście CNN obejmuje rozwiązania problemów rozpoznawania. Czołowe firmy, takie jak Google i Facebook, zainwestowały w projekty badawczo-rozwojowe projektów rozpoznawczych, aby szybciej wykonywać działania.

Każda konwolucyjna sieć neuronowa obejmuje trzy podstawowe idee -

• Lokalne odpowiednie pola
• Convolution
• Pooling

Rozumiemy szczegółowo każdą z tych terminologii.

Odpowiednie pola lokalne

CNN wykorzystuje korelacje przestrzenne, które istnieją w danych wejściowych. Każda z równoległych warstw sieci neuronowych łączy niektóre neurony wejściowe. Ten konkretny region nazywany jest lokalnym polem odbioru. Skupia się tylko na ukrytych neuronach. Ukryty neuron będzie przetwarzał dane wejściowe wewnątrz wspomnianego pola, nie zdając sobie sprawy ze zmian poza określonymi granicami.

Schemat generowania odpowiednich pól lokalnych jest wymieniony poniżej -

Skręt

Na powyższym rysunku widzimy, że każde połączenie uczy się wagi ukrytego neuronu z powiązanym połączeniem z ruchem z jednej warstwy do drugiej. Tutaj poszczególne neurony od czasu do czasu dokonują przesunięcia. Ten proces nazywa się „konwolucją”.

Mapowanie połączeń z warstwy wejściowej do mapy obiektów ukrytych jest definiowane jako „współdzielone wagi”, a uwzględnione odchylenie jest nazywane „współdzielonym odchyleniem”.

Pooling

Konwolucyjne sieci neuronowe wykorzystują warstwy puli, które są umieszczane bezpośrednio po deklaracji CNN. Pobiera dane wejściowe od użytkownika jako mapę cech, która wychodzi z sieci konwolucyjnych i przygotowuje skondensowaną mapę cech. Łączenie warstw pomaga w tworzeniu warstw z neuronami z poprzednich warstw.

Wdrożenie PyTorch

Poniższe kroki służą do tworzenia konwolucyjnej sieci neuronowej za pomocą PyTorch.

Krok 1

Zaimportuj niezbędne pakiety do tworzenia prostej sieci neuronowej.

from torch.autograd import Variable
import torch.nn.functional as F

Krok 2

Utwórz klasę z zbiorczą reprezentacją konwolucyjnej sieci neuronowej. Nasz kształt wsadu dla danych wejściowych x ma wymiar (3, 32, 32).

class SimpleCNN(torch.nn.Module):
   def __init__(self):
      super(SimpleCNN, self).__init__()
      #Input channels = 3, output channels = 18
      self.conv1 = torch.nn.Conv2d(3, 18, kernel_size = 3, stride = 1, padding = 1)
      self.pool = torch.nn.MaxPool2d(kernel_size = 2, stride = 2, padding = 0)
      #4608 input features, 64 output features (see sizing flow below)
      self.fc1 = torch.nn.Linear(18 * 16 * 16, 64)
      #64 input features, 10 output features for our 10 defined classes
      self.fc2 = torch.nn.Linear(64, 10)

Krok 3

Obliczyć aktywację zmian rozmiaru pierwszego splotu od (3, 32, 32) do (18, 32, 32).

Rozmiar wymiaru zmienia się od (18, 32, 32) do (18, 16, 16). Przekształć wymiar danych warstwy wejściowej sieci neuronowej, dzięki czemu rozmiar zmienia się z (18, 16, 16) do (1, 4608).

Przypomnij sobie, że -1 wnioskuje ten wymiar z innego podanego wymiaru.

def forward(self, x):
   x = F.relu(self.conv1(x))
   x = self.pool(x)
   x = x.view(-1, 18 * 16 *16)
   x = F.relu(self.fc1(x))
   #Computes the second fully connected layer (activation applied later)
   #Size changes from (1, 64) to (1, 10)
   x = self.fc2(x)
   return(x)

Powtarzające się sieci neuronowe to jeden z rodzajów algorytmów zorientowanych na głębokie uczenie się, które są oparte na podejściu sekwencyjnym. W sieciach neuronowych zawsze zakładamy, że każde wejście i wyjście jest niezależne od wszystkich innych warstw. Tego typu sieci neuronowe nazywane są rekurencyjnymi, ponieważ wykonują obliczenia matematyczne w sposób sekwencyjny, wykonując jedno zadanie po drugim.

Poniższy diagram przedstawia pełne podejście i działanie powtarzających się sieci neuronowych -

Na powyższym rysunku c1, c2, c3 i x1 są uważane za dane wejściowe, które zawierają pewne ukryte wartości wejściowe, mianowicie h1, h2 i h3, dostarczające odpowiednie wyjście o1. Skoncentrujemy się teraz na wdrożeniu PyTorch do tworzenia fali sinusoidalnej za pomocą powtarzających się sieci neuronowych.

Podczas szkolenia będziemy postępować zgodnie z podejściem szkoleniowym do naszego modelu z jednym punktem danych na raz. Sekwencja wejściowa x składa się z 20 punktów danych, a sekwencja docelowa jest uważana za taką samą, jak sekwencja wejściowa.

Krok 1

Zaimportuj niezbędne pakiety do implementacji powtarzających się sieci neuronowych za pomocą poniższego kodu -

import torch
from torch.autograd import Variable
import numpy as np
import pylab as pl
import torch.nn.init as init

Krok 2

Ustawimy hiperparametry modelu z rozmiarem warstwy wejściowej ustawionym na 7. Będzie 6 neuronów kontekstowych i 1 neuron wejściowy do tworzenia sekwencji docelowej.

dtype = torch.FloatTensor
input_size, hidden_size, output_size = 7, 6, 1
epochs = 300
seq_length = 20
lr = 0.1
data_time_steps = np.linspace(2, 10, seq_length + 1)
data = np.sin(data_time_steps)
data.resize((seq_length + 1, 1))

x = Variable(torch.Tensor(data[:-1]).type(dtype), requires_grad=False)
y = Variable(torch.Tensor(data[1:]).type(dtype), requires_grad=False)

Wygenerujemy dane treningowe, gdzie x jest sekwencją danych wejściowych, a y jest sekwencją docelową.

Krok 3

Wagi są inicjalizowane w powtarzającej się sieci neuronowej przy użyciu rozkładu normalnego z zerową średnią. W1 będzie reprezentować akceptację zmiennych wejściowych, a w2 będzie reprezentować wynik, który jest generowany, jak pokazano poniżej -

w1 = torch.FloatTensor(input_size, 
hidden_size).type(dtype)
init.normal(w1, 0.0, 0.4)
w1 = Variable(w1, requires_grad = True)
w2 = torch.FloatTensor(hidden_size, output_size).type(dtype)
init.normal(w2, 0.0, 0.3)
w2 = Variable(w2, requires_grad = True)

Krok 4

Teraz ważne jest, aby utworzyć funkcję sprzężenia zwrotnego, która jednoznacznie definiuje sieć neuronową.

def forward(input, context_state, w1, w2):
   xh = torch.cat((input, context_state), 1)
   context_state = torch.tanh(xh.mm(w1))
   out = context_state.mm(w2)
   return (out, context_state)

Krok 5

Kolejnym krokiem jest rozpoczęcie procedury szkoleniowej implementacji rekurencyjnej fali sinusoidalnej w sieci neuronowej. Pętla zewnętrzna wykonuje iterację po każdej pętli, a pętla wewnętrzna przechodzi przez element sekwencji. Tutaj obliczymy również średni kwadratowy błąd (MSE), który pomaga w przewidywaniu zmiennych ciągłych.

for i in range(epochs):
   total_loss = 0
   context_state = Variable(torch.zeros((1, hidden_size)).type(dtype), requires_grad = True)
   for j in range(x.size(0)):
      input = x[j:(j+1)]
      target = y[j:(j+1)]
      (pred, context_state) = forward(input, context_state, w1, w2)
      loss = (pred - target).pow(2).sum()/2
      total_loss += loss
      loss.backward()
      w1.data -= lr * w1.grad.data
      w2.data -= lr * w2.grad.data
      w1.grad.data.zero_()
      w2.grad.data.zero_()
      context_state = Variable(context_state.data)
   if i % 10 == 0:
      print("Epoch: {} loss {}".format(i, total_loss.data[0]))

context_state = Variable(torch.zeros((1, hidden_size)).type(dtype), requires_grad = False)
predictions = []

for i in range(x.size(0)):
   input = x[i:i+1]
   (pred, context_state) = forward(input, context_state, w1, w2)
   context_state = context_state
   predictions.append(pred.data.numpy().ravel()[0])

Krok 6

Teraz nadszedł czas, aby wykreślić falę sinusoidalną tak, jak jest potrzebna.

pl.scatter(data_time_steps[:-1], x.data.numpy(), s = 90, label = "Actual")
pl.scatter(data_time_steps[1:], predictions, label = "Predicted")
pl.legend()
pl.show()

Wynik

Wynik powyższego procesu jest następujący -

W tym rozdziale skupimy się bardziej na torchvision.datasetsi jego różne typy. PyTorch zawiera następujące programy ładujące zestawy danych -

• MNIST
• COCO (napisy i wykrywanie)

Zbiór danych zawiera większość dwóch typów funkcji podanych poniżej -

• Transform- funkcja, która pobiera obraz i zwraca zmodyfikowaną wersję standardowej rzeczy. Można je komponować razem z transformacjami.

• Target_transform- funkcja, która przyjmuje cel i przekształca go. Na przykład pobiera napis podpisu i zwraca tensor światowych indeksów.

MNIST

Poniżej znajduje się przykładowy kod zestawu danych MNIST -

dset.MNIST(root, train = TRUE, transform = NONE, 
target_transform = None, download = FALSE)

Parametry są następujące -

• root - katalog główny zbioru danych, w którym istnieją przetworzone dane.

• train - True = zestaw treningowy, False = zestaw testowy

• download - True = pobiera zestaw danych z Internetu i umieszcza go w katalogu głównym.

KOKOSOWIEC

Wymaga to zainstalowania API COCO. Poniższy przykład służy do zademonstrowania implementacji zestawu danych COCO przy użyciu PyTorch -

import torchvision.dataset as dset
import torchvision.transforms as transforms
cap = dset.CocoCaptions(root = ‘ dir where images are’, 
annFile = ’json annotation file’,
transform = transforms.ToTensor())
print(‘Number of samples: ‘, len(cap))
print(target)

Osiągnięty wynik jest następujący -

Number of samples: 82783
Image Size: (3L, 427L, 640L)

Convents to budowa modelu CNN od podstaw. Architektura sieci będzie zawierała kombinację następujących kroków -

• Conv2d
• MaxPool2d
• Rektyfikowana jednostka liniowa
• View
• Warstwa liniowa

Trenowanie modelu

Uczenie modelu jest tym samym procesem, co problemy z klasyfikacją obrazu. Poniższy fragment kodu kończy procedurę modelu szkoleniowego na podanym zestawie danych -

def fit(epoch,model,data_loader,phase 
= 'training',volatile = False):
   if phase == 'training':
      model.train()
   if phase == 'training':
      model.train()
   if phase == 'validation':
      model.eval()
   volatile=True
   running_loss = 0.0
   running_correct = 0
   for batch_idx , (data,target) in enumerate(data_loader):
      if is_cuda:
         data,target = data.cuda(),target.cuda()
         data , target = Variable(data,volatile),Variable(target)
      if phase == 'training':
         optimizer.zero_grad()
         output = model(data)
         loss = F.nll_loss(output,target)
         running_loss + = 
         F.nll_loss(output,target,size_average = 
         False).data[0]
         preds = output.data.max(dim = 1,keepdim = True)[1]
         running_correct + = 
         preds.eq(target.data.view_as(preds)).cpu().sum()
         if phase == 'training':
            loss.backward()
            optimizer.step()
   loss = running_loss/len(data_loader.dataset)
   accuracy = 100. * running_correct/len(data_loader.dataset)
   print(f'{phase} loss is {loss:{5}.{2}} and {phase} accuracy is {running_correct}/{len(data_loader.dataset)}{accuracy:{return loss,accuracy}})

Metoda obejmuje inną logikę szkolenia i walidacji. Istnieją dwa główne powody używania różnych trybów -

• W trybie pociągu porzucenie usuwa pewien procent wartości, co nie powinno mieć miejsca w fazie walidacji lub testowania.

• W przypadku trybu uczenia obliczamy gradienty i zmieniamy wartości parametrów modelu, ale propagacja wsteczna nie jest wymagana podczas faz testowania lub walidacji.

W tym rozdziale skupimy się na stworzeniu klasztoru od podstaw. Wynika to z utworzenia odpowiedniego klasztoru lub przykładowej sieci neuronowej za pomocą pochodni.

Krok 1

Utwórz niezbędną klasę z odpowiednimi parametrami. Parametry obejmują wagi o losowej wartości.

class Neural_Network(nn.Module):
   def __init__(self, ):
      super(Neural_Network, self).__init__()
      self.inputSize = 2
      self.outputSize = 1
      self.hiddenSize = 3
      # weights
      self.W1 = torch.randn(self.inputSize, 
      self.hiddenSize) # 3 X 2 tensor
      self.W2 = torch.randn(self.hiddenSize, self.outputSize) # 3 X 1 tensor

Krok 2

Utwórz wzór sprzężenia zwrotnego funkcji z funkcjami sigmoidalnymi.

def forward(self, X):
   self.z = torch.matmul(X, self.W1) # 3 X 3 ".dot" 
   does not broadcast in PyTorch
   self.z2 = self.sigmoid(self.z) # activation function
   self.z3 = torch.matmul(self.z2, self.W2)
   o = self.sigmoid(self.z3) # final activation 
   function
   return o
   def sigmoid(self, s):
      return 1 / (1 + torch.exp(-s))
   def sigmoidPrime(self, s):
      # derivative of sigmoid
      return s * (1 - s)
   def backward(self, X, y, o):
      self.o_error = y - o # error in output
      self.o_delta = self.o_error * self.sigmoidPrime(o) # derivative of sig to error
      self.z2_error = torch.matmul(self.o_delta, torch.t(self.W2))
      self.z2_delta = self.z2_error * self.sigmoidPrime(self.z2)
      self.W1 + = torch.matmul(torch.t(X), self.z2_delta)
      self.W2 + = torch.matmul(torch.t(self.z2), self.o_delta)

Krok 3

Utwórz model szkolenia i prognozowania, jak wspomniano poniżej -

def train(self, X, y):
   # forward + backward pass for training
   o = self.forward(X)
   self.backward(X, y, o)
def saveWeights(self, model):
   # Implement PyTorch internal storage functions
   torch.save(model, "NN")
   # you can reload model with all the weights and so forth with:
   # torch.load("NN")
def predict(self):
   print ("Predicted data based on trained weights: ")
   print ("Input (scaled): \n" + str(xPredicted))
   print ("Output: \n" + str(self.forward(xPredicted)))

Konwolucyjne sieci neuronowe obejmują główną cechę, extraction. Poniższe kroki służą do zaimplementowania ekstrakcji cech konwolucyjnej sieci neuronowej.

Krok 1

Zaimportuj odpowiednie modele, aby utworzyć model ekstrakcji cech za pomocą „PyTorch”.

import torch
import torch.nn as nn
from torchvision import models

Krok 2

Utwórz klasę ekstraktora elementów, którą można wywołać w razie potrzeby.

class Feature_extractor(nn.module):
   def forward(self, input):
      self.feature = input.clone()
      return input
new_net = nn.Sequential().cuda() # the new network
target_layers = [conv_1, conv_2, conv_4] # layers you want to extract`
i = 1
for layer in list(cnn):
   if isinstance(layer,nn.Conv2d):
      name = "conv_"+str(i)
      art_net.add_module(name,layer)
      if name in target_layers:
         new_net.add_module("extractor_"+str(i),Feature_extractor())
      i+=1
   if isinstance(layer,nn.ReLU):
      name = "relu_"+str(i)
      new_net.add_module(name,layer)
   if isinstance(layer,nn.MaxPool2d):
      name = "pool_"+str(i)
      new_net.add_module(name,layer)
new_net.forward(your_image)
print (new_net.extractor_3.feature)

W tym rozdziale skupimy się na modelu wizualizacji danych przy pomocy konwentów. Aby uzyskać doskonały obraz wizualizacji za pomocą konwencjonalnej sieci neuronowej, wymagane są następujące kroki.

Krok 1

Zaimportuj niezbędne moduły, które są ważne przy wizualizacji konwencjonalnych sieci neuronowych.

import os
import numpy as np
import pandas as pd
from scipy.misc import imread
from sklearn.metrics import accuracy_score

import keras
from keras.models import Sequential, Model
from keras.layers import Dense, Dropout, Flatten, Activation, Input
from keras.layers import Conv2D, MaxPooling2D
import torch

Krok 2

Aby zatrzymać potencjalną przypadkowość z danymi treningowymi i testowymi, wywołaj odpowiedni zestaw danych podany w poniższym kodzie -

seed = 128
rng = np.random.RandomState(seed)
data_dir = "../../datasets/MNIST"
train = pd.read_csv('../../datasets/MNIST/train.csv')
test = pd.read_csv('../../datasets/MNIST/Test_fCbTej3.csv')
img_name = rng.choice(train.filename)
filepath = os.path.join(data_dir, 'train', img_name)
img = imread(filepath, flatten=True)

Krok 3

Narysuj niezbędne obrazy, aby uzyskać dane treningowe i testowe zdefiniowane w doskonały sposób za pomocą poniższego kodu -

pylab.imshow(img, cmap ='gray')
pylab.axis('off')
pylab.show()

Wynik jest wyświetlany jak poniżej -

W tym rozdziale proponujemy alternatywne podejście, które zamiast tego opiera się na pojedynczej splotowej sieci neuronowej 2D w obu sekwencjach. Każda warstwa naszej sieci ponownie koduje tokeny źródłowe na podstawie dotychczas wyprodukowanej sekwencji wyjściowej. Właściwości przypominające uwagę są zatem wszechobecne w całej sieci.

Tutaj skupimy się na creating the sequential network with specific pooling from the values included in dataset. Ten proces najlepiej zastosować również w „module rozpoznawania obrazu”.

Poniższe kroki służą do tworzenia modelu przetwarzania sekwencji z konwentów przy użyciu PyTorch -

Krok 1

Zaimportuj niezbędne moduły do ​​przetwarzania sekwencji przy użyciu konwentów.

import keras 
from keras.datasets import mnist 
from keras.models import Sequential 
from keras.layers import Dense, Dropout, Flatten 
from keras.layers import Conv2D, MaxPooling2D 
import numpy as np

Krok 2

Wykonaj niezbędne operacje, aby utworzyć wzór w odpowiedniej kolejności, używając poniższego kodu -

batch_size = 128 
num_classes = 10 
epochs = 12
# input image dimensions 
img_rows, img_cols = 28, 28
# the data, split between train and test sets 
(x_train, y_train), (x_test, y_test) = mnist.load_data()
x_train = x_train.reshape(60000,28,28,1) 
x_test = x_test.reshape(10000,28,28,1)
print('x_train shape:', x_train.shape) 
print(x_train.shape[0], 'train samples') 
print(x_test.shape[0], 'test samples')
y_train = keras.utils.to_categorical(y_train, num_classes) 
y_test = keras.utils.to_categorical(y_test, num_classes)

Krok 3

Skompiluj model i dopasuj wzór do wspomnianego konwencjonalnego modelu sieci neuronowej, jak pokazano poniżej -

model.compile(loss = 
keras.losses.categorical_crossentropy, 
optimizer = keras.optimizers.Adadelta(), metrics = 
['accuracy'])
model.fit(x_train, y_train, 
batch_size = batch_size, epochs = epochs, 
verbose = 1, validation_data = (x_test, y_test)) 
score = model.evaluate(x_test, y_test, verbose = 0) 
print('Test loss:', score[0]) 
print('Test accuracy:', score[1])

Wygenerowane dane wyjściowe są następujące -

W tym rozdziale zrozumiemy słynny model osadzania słowa - word2vec. Model Word2vec służy do tworzenia osadzania słów za pomocą grupy powiązanych modeli. Model Word2vec jest implementowany przy użyciu czystego kodu C, a gradient jest obliczany ręcznie.

Implementację modelu word2vec w PyTorch wyjaśniono w poniższych krokach -

Krok 1

Zaimplementuj biblioteki w osadzaniu słów, jak wspomniano poniżej -

import torch
from torch.autograd import Variable
import torch.nn as nn
import torch.nn.functional as F

Krok 2

Zaimplementuj model Skip Gram osadzania słów z klasą o nazwie word2vec. Obejmujeemb_size, emb_dimension, u_embedding, v_embedding rodzaj atrybutów.

class SkipGramModel(nn.Module):
   def __init__(self, emb_size, emb_dimension):
      super(SkipGramModel, self).__init__()
      self.emb_size = emb_size
      self.emb_dimension = emb_dimension
      self.u_embeddings = nn.Embedding(emb_size, emb_dimension, sparse=True)
      self.v_embeddings = nn.Embedding(emb_size, emb_dimension, sparse = True)
      self.init_emb()
   def init_emb(self):
      initrange = 0.5 / self.emb_dimension
      self.u_embeddings.weight.data.uniform_(-initrange, initrange)
      self.v_embeddings.weight.data.uniform_(-0, 0)
   def forward(self, pos_u, pos_v, neg_v):
      emb_u = self.u_embeddings(pos_u)
      emb_v = self.v_embeddings(pos_v)
      score = torch.mul(emb_u, emb_v).squeeze()
      score = torch.sum(score, dim = 1)
      score = F.logsigmoid(score)
      neg_emb_v = self.v_embeddings(neg_v)
      neg_score = torch.bmm(neg_emb_v, emb_u.unsqueeze(2)).squeeze()
      neg_score = F.logsigmoid(-1 * neg_score)
      return -1 * (torch.sum(score)+torch.sum(neg_score))
   def save_embedding(self, id2word, file_name, use_cuda):
      if use_cuda:
         embedding = self.u_embeddings.weight.cpu().data.numpy()
      else:
         embedding = self.u_embeddings.weight.data.numpy()
      fout = open(file_name, 'w')
      fout.write('%d %d\n' % (len(id2word), self.emb_dimension))
      for wid, w in id2word.items():
         e = embedding[wid]
         e = ' '.join(map(lambda x: str(x), e))
         fout.write('%s %s\n' % (w, e))
def test():
   model = SkipGramModel(100, 100)
   id2word = dict()
   for i in range(100):
      id2word[i] = str(i)
   model.save_embedding(id2word)

Krok 3

Zaimplementuj główną metodę, aby poprawnie wyświetlić model osadzania słów.

if __name__  ==  '__main__':
   test()

Głębokie sieci neuronowe mają wyjątkową funkcję umożliwiającą przełom w uczeniu maszynowym rozumienia procesu języka naturalnego. Zaobserwowano, że większość tych modeli traktuje język jako płaską sekwencję słów lub znaków i używa pewnego rodzaju modelu, który jest określany jako rekurencyjna sieć neuronowa lub RNN.

Wielu badaczy dochodzi do wniosku, że język najlepiej jest rozumieć w odniesieniu do hierarchicznego drzewa fraz. Ten typ jest zawarty w rekurencyjnych sieciach neuronowych, które uwzględniają określoną strukturę.

PyTorch ma specyficzną funkcję, która pomaga znacznie ułatwić te złożone modele przetwarzania języka naturalnego. Jest to w pełni funkcjonalna platforma do wszelkiego rodzaju głębokiego uczenia z silnym wsparciem dla widzenia komputerowego.

Cechy rekurencyjnej sieci neuronowej

• Rekurencyjna sieć neuronowa jest tworzona w taki sposób, że obejmuje stosowanie tego samego zestawu wag z różnymi strukturami graficznymi.

• Węzły są przemierzane w porządku topologicznym.

• Ten typ sieci jest uczony przez odwrotny tryb automatycznego różnicowania.

• Przetwarzanie języka naturalnego obejmuje szczególny przypadek rekurencyjnych sieci neuronowych.

• Ta rekurencyjna sieć tensorów neuronowych obejmuje różne węzły funkcjonalne w drzewie.

Przykład rekurencyjnej sieci neuronowej przedstawiono poniżej -