Analiza danych pomiarowych oprogramowania
Po zebraniu odpowiednich danych musimy je odpowiednio przeanalizować. Przy wyborze techniki analizy należy wziąć pod uwagę trzy główne elementy.
- Charakter danych
- Cel eksperymentu
- Rozważania projektowe
Charakter danych
Aby przeanalizować dane, musimy również przyjrzeć się większej populacji reprezentowanej przez dane, a także rozkładowi tych danych.
Pobieranie próbek, populacja i dystrybucja danych
Próbkowanie to proces wybierania zestawu danych z dużej populacji. Przykładowe statystyki opisują i podsumowują pomiary uzyskane od grupy badanych eksperymentalnych.
Parametry populacji reprezentują wartości, które zostałyby uzyskane, gdyby mierzono wszystkie możliwe osoby.
Populację lub próbę można opisać za pomocą miar tendencji centralnej, takich jak średnia, mediana i tryb, oraz miar dyspersji, takich jak wariancja i odchylenie standardowe. Wiele zestawów danych jest dystrybuowanych normalnie, jak pokazano na poniższym wykresie.
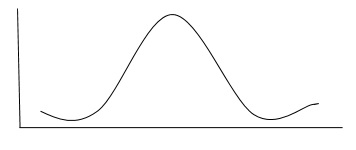
Jak pokazano powyżej, dane będą równomiernie rozłożone na temat średniej. co jest istotną cechą rozkładu normalnego.
Istnieją również inne rozkłady, w których dane są wypaczone, tak że po jednej stronie średniej znajduje się więcej punktów danych niż po drugiej. Na przykład: jeśli większość danych znajduje się po lewej stronie średniej, możemy powiedzieć, że rozkład jest skośny w lewo.
Cel eksperymentu
Zwykle przeprowadza się eksperymenty -
- Aby potwierdzić teorię
- Aby zbadać związek
Aby osiągnąć każdy z tych celów, cel należy formalnie wyrazić za pomocą hipotezy, a analiza musi bezpośrednio odnosić się do hipotezy.
Aby potwierdzić teorię
Badanie musi mieć na celu zbadanie prawdy teorii. Teoria zwykle stwierdza, że użycie określonej metody, narzędzia lub techniki ma szczególny wpływ na badanych, czyniąc je w pewnym sensie lepszymi od innych.
Należy wziąć pod uwagę dwa przypadki danych: normal data i non-normal data.
Jeśli dane pochodzą z rozkładu normalnego i istnieją dwie grupy do porównania, do analizy można użyć testu t-Studenta. Jeśli do porównania są więcej niż dwie grupy, można zastosować ogólną analizę testu wariancji zwaną statystyką F.
Jeśli dane nie są normalne, można je przeanalizować za pomocą testu Kruskala-Wallisa, oceniając je.
Aby zbadać związek
Badania mają na celu określenie związku między punktami danych opisującymi jedną zmienną lub wiele zmiennych.
Istnieją trzy techniki udzielania odpowiedzi na pytania dotyczące relacji: wykresy pudełkowe, wykresy punktowe i analiza korelacji.
ZA box plot może reprezentować podsumowanie zakresu zbioru danych.
ZA scatter plot reprezentuje związek między dwiema zmiennymi.
Correlation analysis używa metod statystycznych, aby potwierdzić, czy istnieje prawdziwy związek między dwoma atrybutami.
Dla wartości o rozkładzie normalnym użyj Pearson Correlation Coefficient aby sprawdzić, czy te dwie zmienne są wysoce skorelowane.
W przypadku danych innych niż normalne ustaw ranking danych i użyj rozszerzenia Spearman Rank Correlation Coefficientjako miara skojarzenia. Inną miarą dla niestandardowych danych jestKendall robust correlation coefficient, który bada związek między parami punktów danych i może zidentyfikować częściową korelację.
Jeśli ranking zawiera dużą liczbę powiązanych wartości, a chi-squared testw tabeli kontyngencji można użyć do przetestowania powiązania między zmiennymi. Podobnie,linear regression może posłużyć do wygenerowania równania opisującego związek między zmiennymi.
W przypadku więcej niż dwóch zmiennych multivariate regression może być zastosowane.
Uwagi projektowe
Wybierając techniki analizy, należy wziąć pod uwagę projekt badania. Jednocześnie złożoność analizy może wpłynąć na wybrany projekt. Wiele grup używa statystyk F zamiast testu t-Studenta w dwóch grupach.
W przypadku złożonych planów czynnikowych z więcej niż dwoma czynnikami potrzebny jest bardziej zaawansowany test powiązania i istotności.
Techniki statystyczne można wykorzystać do wyjaśnienia wpływu jednego zestawu zmiennych na inne lub do skompensowania efektów czasowych lub uczenia się.