Volume de um sólido feito de cubos com comprimentos de borda de unidade de fração

Introdução

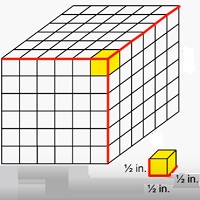
Aqui encontramos o volume de sólidos feitos de cubos com comprimentos de borda de fração unitária. Considere, por exemplo, um sólido de dimensões 3 pol x 3 pol x 3 feito de pequenos cubos com comprimentos de aresta de $ \ frac {1} {2} $ polegadas.

Nesse caso, o sólido é feito de 6 × 6 × 6 pequenos cubos de $ \ frac {1} {2} $ polegadas de comprimento de aresta. Portanto, o volume do sólido, neste caso, seria

Volume = lwh = $ 6 \ times \ frac {1} {2} \ times 6 \ times \ frac {1} {2} \ times 6 \ times \ frac {1} {2} $

= 3 × 3 × 3 = 27 polegadas cúbicas

Fórmula para o volume do sólido feito de cubos com comprimentos de borda fracionários unitários

Supondo que o sólido seja um cubo de unidades de aresta

b = número de cubos com comprimento de borda fracionário unitário ao longo de cada borda

k = comprimento da borda fracionária unitária

Volume of solid = b × k × b × k × b × k cubic units

Exemplo 1

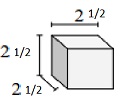
Encontre o volume do seguinte sólido de cubos com comprimentos de borda de fração unitária. Cada unidade de prismas é medida em cm (sem escala)

Solução

Step 1:

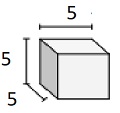
Sólido de cubos com comprimentos de borda de fração unitária de $ \ frac {1} {2} $ cm

Step 2:

Volume V = lwh = $ 2 \ frac {1} {2} \ vezes 2 \ frac {1} {2} \ vezes 2 \ frac {1} {2} $

= $ 5 \ times \ frac {1} {2} \ times 5 \ times \ frac {1} {2} \ times 5 \ times \ frac {1} {2} $

= $ 15 \ frac {5} {8} $ cu cm

Exemplo 2

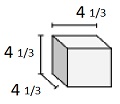
Encontre o volume do seguinte sólido de cubos com comprimentos de borda de fração unitária. Cada unidade de prismas é medida em cm (sem escala)

Solução

Step 1:

Sólido de cubos com comprimentos de borda de fração unitária de $ \ frac {1} {3} $ cm

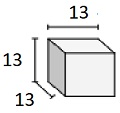
Step 2:

Volume V = lwh = $ 4 \ frac {1} {3} \ vezes 4 \ frac {1} {3} \ vezes 4 \ frac {1} {3} $

= $ 13 \ times \ frac {1} {3} \ times 13 \ times \ frac {1} {3} \ times 13 \ times \ frac {1} {3} $

= $ 81 \ frac {10} {27} $ cu cm