Bokeh - curvas especializadas

o bokeh.plotting API oferece suporte a métodos de renderização seguindo curvas especializadas -

beizer ()

Este método adiciona uma curva de Bézier ao objeto de figura. Uma curva de Bézier é uma curva paramétrica usada em computação gráfica. Outros usos incluem o design de fontes e animação de computador, design de interface de usuário e para suavizar a trajetória do cursor.

Em gráficos vetoriais, as curvas de Bézier são usadas para modelar curvas suaves que podem ser dimensionadas indefinidamente. Um "Caminho" é uma combinação de curvas de Bézier vinculadas.

O método beizer () tem os seguintes parâmetros que são definidos -

1	x0	As coordenadas x dos pontos de partida.
2	y0	As coordenadas y dos pontos de partida ..
3	x1	As coordenadas x dos pontos finais.
4	y1	As coordenadas y dos pontos finais.
5	cx0	As coordenadas x dos primeiros pontos de controle.
6	cy0	As coordenadas y dos primeiros pontos de controle.
7	cx1	As coordenadas x dos segundos pontos de controle.
8	cy1	As coordenadas y dos segundos pontos de controle.

O valor padrão para todos os parâmetros é Nenhum.

Exemplo

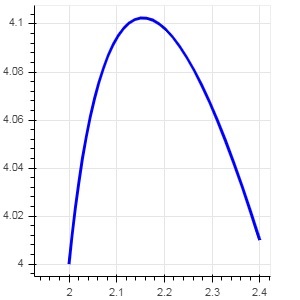
O código a seguir gera uma página HTML mostrando uma curva de Bézier e parábola no gráfico Bokeh -

x = 2
y = 4
xp02 = x+0.4
xp01 = x+0.1
xm01 = x-0.1
yp01 = y+0.2
ym01 = y-0.2
fig = figure(plot_width = 300, plot_height = 300)
fig.bezier(x0 = x, y0 = y, x1 = xp02, y1 = y, cx0 = xp01, cy0 = yp01,
cx1 = xm01, cy1 = ym01, line_color = "red", line_width = 2)

Resultado

quadrático()

Este método adiciona um parabola glyphpara bokeh figura. A função tem os mesmos parâmetros de beizer (), excetocx0 e cx1.

Exemplo

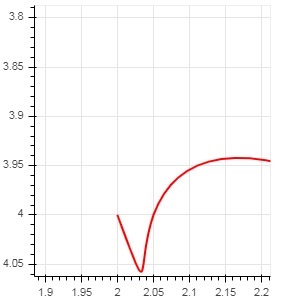
O código fornecido a seguir gera uma curva quadrática.

x = 2
y = 4
xp02 = x + 0.3
xp01 = x + 0.2
xm01 = x - 0.4
yp01 = y + 0.1
ym01 = y - 0.2
x = x,
y = y,
xp02 = x + 0.4,
xp01 = x + 0.1,
yp01 = y + 0.2,
fig.quadratic(x0 = x, y0 = y, x1 = x + 0.4, y1 = y + 0.01, cx = x + 0.1,
cy = y + 0.2, line_color = "blue", line_width = 3)

Resultado