Comunicação Digital - Modulação Delta
A taxa de amostragem de um sinal deve ser maior do que a taxa de Nyquist, para obter uma melhor amostragem. Se este intervalo de amostragem no PCM diferencial for reduzido consideravelmente, a diferença de amplitude amostra para amostra é muito pequena, como se a diferença fosse1-bit quantization, então o tamanho do passo será muito pequeno, ou seja, Δ (delta).
Modulação Delta
O tipo de modulação, onde a taxa de amostragem é muito maior e em que o tamanho do passo após a quantização é de um valor menor Δ, tal modulação é denominada como delta modulation.
Características da modulação delta
A seguir estão alguns dos recursos da modulação delta.
Uma entrada sobre-amostrada é usada para fazer uso total da correlação do sinal.
O projeto de quantização é simples.
A sequência de entrada é muito maior do que a taxa de Nyquist.
A qualidade é moderada.
O design do modulador e do demodulador é simples.
A aproximação em escada da forma de onda de saída.
O tamanho do passo é muito pequeno, ou seja, Δ (delta).
A taxa de bits pode ser decidida pelo usuário.
Isso envolve uma implementação mais simples.
A modulação delta é uma forma simplificada da técnica DPCM, também vista como 1-bit DPCM scheme. Conforme o intervalo de amostragem é reduzido, a correlação do sinal será maior.
Modulador Delta
O modulador Delta é composto por um quantizador de 1 bit e um circuito de atraso junto com dois circuitos de verão. A seguir está o diagrama de blocos de um modulador delta.
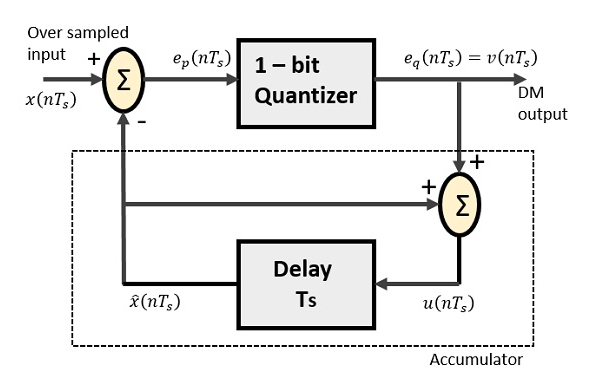
O circuito preditor no DPCM é substituído por um circuito de atraso simples no DM.
No diagrama acima, temos as notações como -
$ x (nT_ {s}) $ = sobre a entrada amostrada
$ e_ {p} (nT_ {s}) $ = saída de verão e entrada do quantizador
$ e_ {q} (nT_ {s}) $ = saída do quantizador = $ v (nT_s) $
$ \ widehat {x} (nT_ {s}) $ = saída do circuito de atraso
$ u (nT_ {s}) $ = entrada do circuito de atraso
Usando essas notações, agora devemos tentar descobrir o processo de modulação delta.
$ e_ {p} (nT_ {s}) = x (nT_ {s}) - \ widehat {x} (nT_ {s}) $
--------- equação 1
$ = x (nT_ {s}) - u ([n - 1] T_ {s}) $
$ = x (nT_ {s}) - [\ widehat {x} [[n - 1] T_ {s}] + v [[n-1] T_ {s}]] $
--------- equação 2
Mais distante,
$ v (nT_ {s}) = e_ {q} (nT_ {s}) = S.sig. [e_ {p} (nT_ {s})] $
--------- equação 3
$ u (nT_ {s}) = \ widehat {x} (nT_ {s}) + e_ {q} (nT_ {s}) $
Onde,
$ \ widehat {x} (nT_ {s}) $ = o valor anterior do circuito de atraso
$ e_ {q} (nT_ {s}) $ = saída do quantizador = $ v (nT_s) $
Conseqüentemente,
$ u (nT_ {s}) = u ([n-1] T_ {s}) + v (nT_ {s}) $
--------- equação 4
Que significa,
The present input of the delay unit
= (The previous output of the delay unit) + (the present quantizer output)
Assumindo a condição zero de acumulação,
$ u (nT_ {s}) = S \ displaystyle \ sum \ limits_ {j = 1} ^ n sig [e_ {p} (jT_ {s})] $
Accumulated version of DM output = $ \ displaystyle \ sum \ limits_ {j = 1} ^ nv (jT_ {s}) $
--------- equação 5
Agora, observe que
$ \ widehat {x} (nT_ {s}) = u ([n-1] T_ {s}) $
$ = \ displaystyle \ sum \ limits_ {j = 1} ^ {n - 1} v (jT_ {s}) $
--------- equação 6
A saída da unidade de atraso é uma saída do acumulador atrasada em uma amostra.
A partir das equações 5 e 6, obtemos uma estrutura possível para o demodulador.
Uma forma de onda aproximada em caso de escada será a saída do modulador delta com o tamanho do passo como delta (Δ) A qualidade de saída da forma de onda é moderada.
Demodulador Delta
O demodulador delta é composto por um filtro passa-baixas, um circuito de verão e um retardo. O circuito preditor é eliminado aqui e, portanto, nenhuma entrada presumida é fornecida ao demodulador.
A seguir está o diagrama para o demodulador delta.
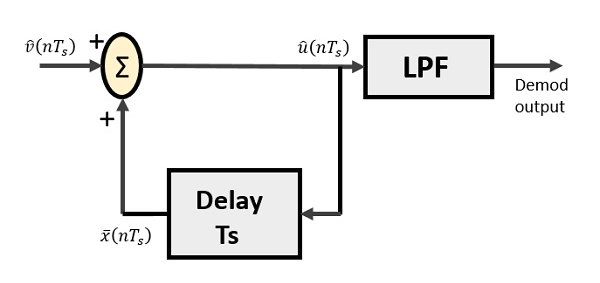
No diagrama acima, temos as notações como -
$ \ widehat {v} (nT_ {s}) $ é a amostra de entrada
$ \ widehat {u} (nT_ {s}) $ é a produção de verão
$ \ bar {x} (nT_ {s}) $ é a saída atrasada
Uma seqüência binária será fornecida como uma entrada para o demodulador. A saída aproximada em escada é fornecida ao LPF.
O filtro passa-baixo é usado por muitos motivos, mas o motivo mais proeminente é a eliminação de ruído para sinais fora da banda. O erro de tamanho do passo que pode ocorrer no transmissor é chamadogranular noise, que é eliminado aqui. Se não houver ruído presente, a saída do modulador será igual à entrada do demodulador.
Vantagens do DM sobre DPCM
Quantizador de 1 bit
Projeto muito fácil do modulador e do demodulador
No entanto, existe algum ruído no DM.
Inclinação sobre distorção de carga (quando Δ é pequeno)
Ruído granular (quando Δ é grande)
Modulação Delta Adaptativa (ADM)
Na modulação digital, encontramos certo problema de determinação do tamanho do passo, que influencia a qualidade da onda de saída.
Um tamanho de passo maior é necessário na inclinação acentuada do sinal de modulação e um tamanho de passo menor é necessário onde a mensagem tem uma inclinação pequena. Os mínimos detalhes são perdidos no processo. Portanto, seria melhor se pudéssemos controlar o ajuste do tamanho do passo, de acordo com nossa necessidade, a fim de obter a amostra da maneira desejada. Este é o conceito deAdaptive Delta Modulation.
A seguir está o diagrama de blocos do modulador delta adaptativo.
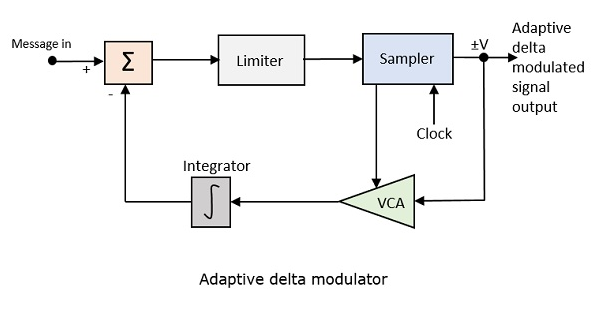
O ganho do amplificador controlado por voltagem é ajustado pelo sinal de saída do amostrador. O ganho do amplificador determina o tamanho do passo e ambos são proporcionais.
O ADM quantiza a diferença entre o valor da amostra atual e o valor previsto da próxima amostra. Ele usa uma altura de degrau variável para prever os próximos valores, para a reprodução fiel dos valores de variação rápida.