Comunicação Digital - Amostragem
Sampling é definido como, “O processo de medição dos valores instantâneos do sinal de tempo contínuo em uma forma discreta”.
Sample é um dado retirado de todos os dados que são contínuos no domínio do tempo.
Quando uma fonte gera um sinal analógico e se este tiver que ser digitalizado, tendo 1s e 0sou seja, alto ou baixo, o sinal deve ser discretizado no tempo. Esta discretização do sinal analógico é chamada de Amostragem.
A figura a seguir indica um sinal de tempo contínuo x (t) e um sinal amostrado xs (t). Quandox (t) é multiplicado por um trem de impulso periódico, o sinal amostrado xs (t) é obtido.
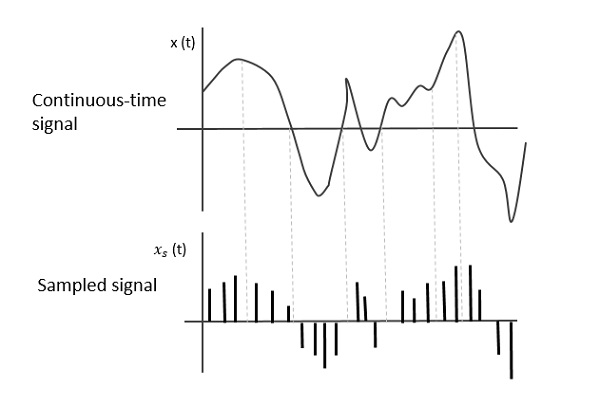
Taxa de amostragem
Para discretizar os sinais, a lacuna entre as amostras deve ser corrigida. Essa lacuna pode ser denominada como umsampling period Ts.
$$ Amostragem \: Frequência = \ frac {1} {T_ {s}} = f_s $$Onde,
$ T_ {s} $ é o tempo de amostragem
$ f_ {s} $ é a frequência de amostragem ou a taxa de amostragem
Sampling frequencyé o recíproco do período de amostragem. Esta frequência de amostragem pode ser simplesmente chamada deSampling rate. A taxa de amostragem denota o número de amostras tomadas por segundo ou para um conjunto finito de valores.
Para que um sinal analógico seja reconstruído a partir do sinal digitalizado, a taxa de amostragem deve ser altamente considerada. A taxa de amostragem deve ser tal que os dados no sinal de mensagem não sejam perdidos nem sejam sobrepostos. Portanto, uma taxa foi fixada para isso, chamada de taxa de Nyquist.
Taxa de Nyquist
Suponha que um sinal seja limitado em banda, sem componentes de frequência superiores a WHertz. Que significa,Wé a frequência mais alta. Para tal sinal, para uma reprodução eficaz do sinal original, a taxa de amostragem deve ser duas vezes a frequência mais alta.
Que significa,
$$ f_ {S} = 2W $$Onde,
$ f_ {S} $ é a taxa de amostragem
W é a frequência mais alta
Esta taxa de amostragem é chamada de Nyquist rate.
Um teorema denominado Teorema da Amostragem foi estabelecido na teoria desta taxa de Nyquist.
Teorema de Amostragem
O teorema da amostragem, que também é chamado de Nyquist theorem, fornece a teoria da taxa de amostragem suficiente em termos de largura de banda para a classe de funções que são limitadas por banda.
O teorema de amostragem afirma que "um sinal pode ser reproduzido exatamente se for amostrado na taxa fs que é maior que o dobro da frequência máxima W. ”
Para entender este teorema de amostragem, vamos considerar um sinal de banda limitada, ou seja, um sinal cujo valor é non-zero entre alguns –W e W Hertz.
Esse sinal é representado como $x(f) = 0 for |f\lvert > W$
Para o sinal de tempo contínuo x (t), o sinal de banda limitada no domínio da frequência, pode ser representado como mostrado na figura a seguir.
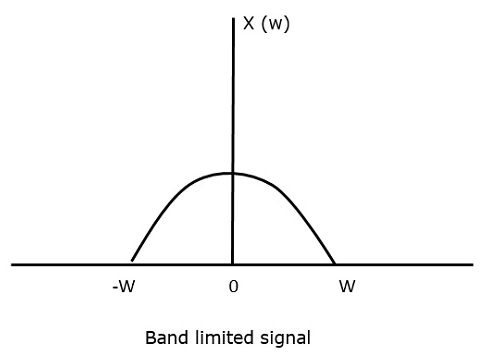
Precisamos de uma frequência de amostragem, uma frequência em que não haja perda de informações, mesmo após a amostragem. Para isso, temos a taxa de Nyquist que a frequência de amostragem deve ser duas vezes a frequência máxima. É a taxa crítica de amostragem.
Se o sinal x(t) é amostrado acima da taxa de Nyquist, o sinal original pode ser recuperado e, se for amostrado abaixo da taxa de Nyquist, o sinal não pode ser recuperado.
A figura a seguir explica um sinal, se amostrado a uma taxa maior do que 2w no domínio da frequência.
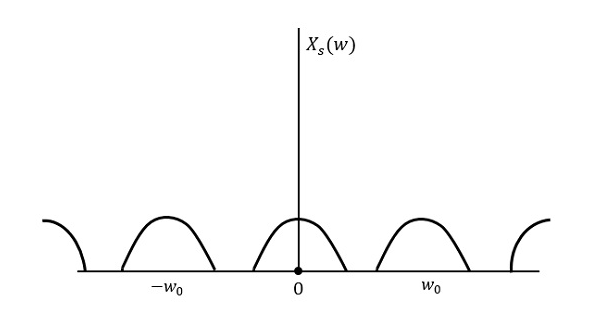
A figura acima mostra a transformada de Fourier de um sinal $x_{s}(t)$. Aqui, as informações são reproduzidas sem qualquer perda. Não há confusão e, portanto, a recuperação é possível.
A transformada de Fourier do sinal $x_{s}(t)$ é
$$ X_ {s} (w) = \ frac {1} {T_ {s}} \ sum_ {n = - \ infty} ^ \ infty X (w-nw_0) $$Onde $ T_ {s} $ = Sampling Period e $ w_ {0} = \ frac {2 \ pi} {T_s} $
Vamos ver o que acontece se a taxa de amostragem for igual a duas vezes a maior frequência (2W)
Que significa,
$$ f_ {s} = 2W $$Onde,
$ f_ {s} $ é a frequência de amostragem
W é a frequência mais alta
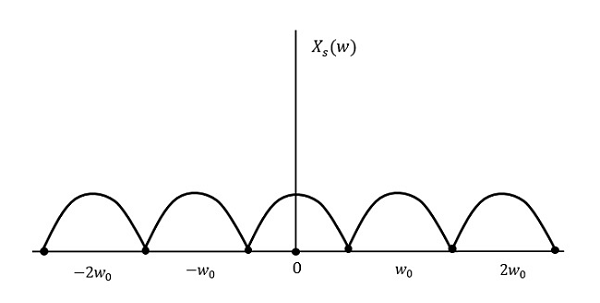
O resultado será como mostrado na figura acima. A informação é substituída sem qualquer perda. Portanto, esta também é uma boa taxa de amostragem.
Agora, vamos olhar para a condição,
$$ f_ {s} <2W $$O padrão resultante será semelhante à figura a seguir.

Podemos observar a partir do padrão acima que a sobreposição de informações é feita, o que leva à confusão e perda de informações. Esse fenômeno indesejado de sobreposição é chamado de Aliasing.
Aliasing
O aliasing pode ser referido como "o fenômeno de um componente de alta frequência no espectro de um sinal, assumindo a identidade de um componente de baixa frequência no espectro de sua versão amostrada".
As medidas corretivas tomadas para reduzir o efeito do aliasing são -
Na seção do transmissor do PCM, um low pass anti-aliasing filter é empregado, antes do amostrador, para eliminar os componentes de alta freqüência indesejados.
O sinal que é amostrado após a filtragem, é amostrado a uma taxa ligeiramente superior à taxa de Nyquist.
Esta escolha de ter uma taxa de amostragem maior do que a taxa de Nyquist, também ajuda no design mais fácil do reconstruction filter no receptor.
Escopo da Transformada de Fourier
Observa-se geralmente que buscamos o auxílio das séries de Fourier e transformadas de Fourier na análise dos sinais e também na prova de teoremas. É porque -
A transformada de Fourier é a extensão da série de Fourier para sinais não periódicos.
A transformada de Fourier é uma ferramenta matemática poderosa que ajuda a visualizar os sinais em diferentes domínios e ajuda a analisar os sinais facilmente.
Qualquer sinal pode ser decomposto em termos de soma de senos e cossenos usando esta transformada de Fourier.
No próximo capítulo, vamos discutir sobre o conceito de Quantização.