Teorema da codificação da fonte
O Código produzido por uma fonte discreta sem memória deve ser representado de forma eficiente, o que é um problema importante nas comunicações. Para que isso aconteça, existem palavras-código, que representam esses códigos-fonte.
Por exemplo, na telegrafia, usamos o código Morse, em que os alfabetos são denotados por Marks e Spaces. Se a cartaE é considerado, que é mais usado, é denotado por “.” Considerando que a carta Q que raramente é usado, é denotado por “--.-”
Vamos dar uma olhada no diagrama de blocos.
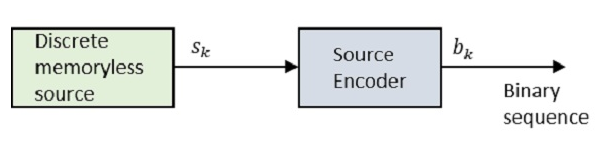
Onde Sk é a saída da fonte discreta sem memória e bk é a saída do codificador de origem, representada por 0s e 1s.
A sequência codificada é tal que é convenientemente decodificada no receptor.
Vamos supor que a fonte tenha um alfabeto com k símbolos diferentes e que o kth símbolo Sk ocorre com a probabilidade Pk, Onde k = 0, 1…k-1.
Deixe a palavra do código binário atribuída ao símbolo Sk, pelo codificador ter comprimento lk, medido em bits.
Portanto, definimos o comprimento médio da palavra de código L do codificador de origem como
$$ \ overline {L} = \ displaystyle \ sum \ limits_ {k = 0} ^ {k-1} p_kl_k $$
L representa o número médio de bits por símbolo de fonte
Se $ L_ {min} = \: mínimo \: possível \: valor \: de \: \ overline {L} $
Então coding efficiency pode ser definido como
$$ \ eta = \ frac {L {min}} {\ overline {L}} $$
Com $ \ overline {L} \ geq L_ {min} $ teremos $ \ eta \ leq 1 $
No entanto, o codificador de origem é considerado eficiente quando $ \ eta = 1 $
Para isso, o valor $ L_ {min} $ deve ser determinado.
Vamos nos referir à definição, “Dada uma fonte discreta sem memória de entropia $ H (\ delta) $, o comprimento médio da palavra-códigoL para qualquer fonte, a codificação é limitada como $ \ overline {L} \ geq H (\ delta) $. "
Em palavras mais simples, a palavra de código (exemplo: código Morse para a palavra QUEUE é -.- ..-. ..-.) É sempre maior ou igual ao código-fonte (QUEUE no exemplo). O que significa que os símbolos na palavra de código são maiores ou iguais aos alfabetos no código-fonte.
Portanto, com $ L_ {min} = H (\ delta) $, a eficiência do codificador de origem em termos de Entropia $ H (\ delta) $ pode ser escrita como
$$ \ eta = \ frac {H (\ delta)} {\ overline {L}} $$
Este teorema de codificação de fonte é chamado de noiseless coding theoremuma vez que estabelece uma codificação sem erros. Também é chamado deShannon’s first theorem.