Matemática Discreta - Guia Rápido

A matemática pode ser amplamente classificada em duas categorias -

• Continuous Mathematics- É baseado na linha numérica contínua ou nos números reais. É caracterizado pelo fato de que entre dois números quaisquer, quase sempre há um conjunto infinito de números. Por exemplo, uma função em matemática contínua pode ser traçada em uma curva suave sem quebras.

• Discrete Mathematics- Envolve valores distintos; ou seja, entre quaisquer dois pontos, há um número contável de pontos. Por exemplo, se tivermos um conjunto finito de objetos, a função pode ser definida como uma lista de pares ordenados com esses objetos e pode ser apresentada como uma lista completa desses pares.

Tópicos em Matemática Discreta

Embora não possa haver um número definido de ramos da Matemática Discreta, os tópicos a seguir são quase sempre cobertos em qualquer estudo sobre este assunto -

• Conjuntos, relações e funções
• Lógica Matemática
• Teoria do grupo
• Teoria de Contagem
• Probability
• Indução matemática e relações de recorrência
• Teoria dos Grafos
• Trees
• Álgebra booleana

Discutiremos cada um desses conceitos nos capítulos subsequentes deste tutorial.

Matemático alemão G. Cantorintroduziu o conceito de conjuntos. Ele definiu um conjunto como uma coleção de objetos definidos e distinguíveis selecionados por meio de certas regras ou descrição.

Seta teoria forma a base de vários outros campos de estudo, como teoria da contagem, relações, teoria dos grafos e máquinas de estado finito. Neste capítulo, iremos cobrir os diferentes aspectos daSet Theory.

Conjunto - Definição

Um conjunto é uma coleção não ordenada de diferentes elementos. Um conjunto pode ser escrito explicitamente listando seus elementos usando colchetes. Se a ordem dos elementos for alterada ou qualquer elemento de um conjunto for repetido, ele não fará nenhuma alteração no conjunto.

Alguns exemplos de conjuntos

• Um conjunto de todos os inteiros positivos
• Um conjunto de todos os planetas do sistema solar
• Um conjunto de todos os estados da Índia
• Um conjunto de todas as letras minúsculas do alfabeto

Representação de um Conjunto

Os conjuntos podem ser representados de duas maneiras -

• Lista ou formulário tabular
• Set Builder Notation

Lista ou formulário tabular

O conjunto é representado listando todos os elementos que o compõem. Os elementos são colocados entre colchetes e separados por vírgulas.

Example 1 - Conjunto de vogais no alfabeto inglês, $A = \lbrace a,e,i,o,u \rbrace$

Example 2 - Conjunto de números ímpares menor que 10, $B = \lbrace 1,3,5,7,9 \rbrace$

Set Builder Notation

O conjunto é definido especificando uma propriedade que os elementos do conjunto têm em comum. O conjunto é descrito como$A = \lbrace x : p(x) \rbrace$

Example 1 - o conjunto $\lbrace a,e,i,o,u \rbrace$ é escrito como -

$A = \lbrace x : \text{x is a vowel in English alphabet} \rbrace$

Example 2 - o conjunto $\lbrace 1,3,5,7,9 \rbrace$ é escrito como -

$B = \lbrace x : 1 \le x \lt 10 \ and\ (x \% 2) \ne 0 \rbrace$

Se um elemento x é membro de qualquer conjunto S, é denotado por $x \in S$ e se um elemento y não é membro do conjunto S, é denotado por $y \notin S$.

Example- se$S = \lbrace1, 1.2, 1.7, 2\rbrace , 1 \in S$ mas $1.5 \notin S$

Alguns conjuntos importantes

N - o conjunto de todos os números naturais = $\lbrace1, 2, 3, 4, .....\rbrace$

Z - o conjunto de todos os inteiros = $\lbrace....., -3, -2, -1, 0, 1, 2, 3, .....\rbrace$

Z⁺ - o conjunto de todos os inteiros positivos

Q - o conjunto de todos os números racionais

R - o conjunto de todos os números reais

W - o conjunto de todos os números inteiros

Cardinalidade de um conjunto

Cardinalidade de um conjunto S, denotada por $|S|$, é o número de elementos do conjunto. O número também é conhecido como número cardinal. Se um conjunto tem um número infinito de elementos, sua cardinalidade é$\infty$.

Example - $|\lbrace 1, 4, 3, 5 \rbrace | = 4, | \lbrace 1, 2, 3, 4, 5, \dots \rbrace | = \infty$

Se houver dois conjuntos X e Y,

• $|X| = |Y|$denota dois conjuntos X e Y com a mesma cardinalidade. Ocorre quando o número de elementos em X é exatamente igual ao número de elementos em Y. Nesse caso, existe uma função bijetiva 'f' de X a Y.

• $|X| \le |Y|$denota que a cardinalidade do conjunto X é menor ou igual à cardinalidade do conjunto Y. Ocorre quando o número de elementos em X é menor ou igual ao de Y. Aqui, existe uma função injetiva 'f' de X a Y.

• $|X| \lt |Y|$denota que a cardinalidade do conjunto X é menor que a cardinalidade do conjunto Y. Ocorre quando o número de elementos em X é menor do que Y. Aqui, a função 'f' de X a Y é injetiva, mas não bijetiva.

• $If\ |X| \le |Y|$ e $|X| \ge |Y|$ então $|X| = |Y|$. Os conjuntos X e Y são comumente chamados de conjuntos equivalentes.

Tipos de conjuntos

Os conjuntos podem ser classificados em vários tipos. Alguns dos quais são finitos, infinitos, subconjuntos, universais, próprios, conjuntos singleton, etc.

Conjunto Finito

Um conjunto que contém um número definido de elementos é chamado de conjunto finito.

Example - $S = \lbrace x \:| \:x \in N$ e $70 \gt x \gt 50 \rbrace$

Conjunto Infinito

Um conjunto que contém um número infinito de elementos é chamado de conjunto infinito.

Example - $S = \lbrace x \: | \: x \in N $ e $ x \gt 10 \rbrace$

Subconjunto

Um conjunto X é um subconjunto do conjunto Y (escrito como $X \subseteq Y$) se cada elemento de X for um elemento do conjunto Y.

Example 1 - Vamos, $X = \lbrace 1, 2, 3, 4, 5, 6 \rbrace$ e $Y = \lbrace 1, 2 \rbrace$. Aqui, o conjunto Y é um subconjunto do conjunto X, pois todos os elementos do conjunto Y estão no conjunto X. Portanto, podemos escrever$Y \subseteq X$.

Example 2 - Vamos, $X = \lbrace 1, 2, 3 \rbrace$ e $Y = \lbrace 1, 2, 3 \rbrace$. Aqui, o conjunto Y é um subconjunto (não é um subconjunto adequado) do conjunto X, pois todos os elementos do conjunto Y estão no conjunto X. Portanto, podemos escrever$Y \subseteq X$.

Subconjunto próprio

O termo “subconjunto adequado” pode ser definido como “subconjunto de, mas não igual a”. Um conjunto X é um subconjunto adequado do conjunto Y (escrito como$ X \subset Y $) se cada elemento de X for um elemento do conjunto Y e $|X| \lt |Y|$.

Example - Vamos, $X = \lbrace 1, 2, 3, 4, 5, 6 \rbrace$ e $Y = \lbrace 1, 2 \rbrace$. Aqui definido$Y \subset X$ uma vez que todos os elementos em $Y$ estão contidos em $X$ também e $X$ tem pelo menos um elemento é mais do que definido $Y$.

Conjunto universal

É uma coleção de todos os elementos em um determinado contexto ou aplicativo. Todos os conjuntos nesse contexto ou aplicativo são essencialmente subconjuntos desse conjunto universal. Conjuntos universais são representados como$U$.

Example - Podemos definir $U$como o conjunto de todos os animais da terra. Neste caso, o conjunto de todos os mamíferos é um subconjunto de$U$, o conjunto de todos os peixes é um subconjunto de $U$, conjunto de todos os insetos é um subconjunto de $U$, e assim por diante.

Conjunto vazio ou conjunto nulo

Um conjunto vazio não contém elementos. É denotado por$\emptyset$. Como o número de elementos em um conjunto vazio é finito, o conjunto vazio é um conjunto finito. A cardinalidade do conjunto vazio ou conjunto nulo é zero.

Example - $S = \lbrace x \:| \: x \in N$ e $7 \lt x \lt 8 \rbrace = \emptyset$

Conjunto de singleton ou conjunto de unidade

Conjunto de singleton ou conjunto de unidades contém apenas um elemento. Um conjunto único é denotado por$\lbrace s \rbrace$.

Example - $S = \lbrace x \:| \:x \in N,\ 7 \lt x \lt 9 \rbrace$ = $\lbrace 8 \rbrace$

Equal Set

Se dois conjuntos contêm os mesmos elementos, eles são considerados iguais.

Example - se $A = \lbrace 1, 2, 6 \rbrace$ e $B = \lbrace 6, 1, 2 \rbrace$, eles são iguais, pois cada elemento do conjunto A é um elemento do conjunto B e cada elemento do conjunto B é um elemento do conjunto A.

Conjunto Equivalente

Se as cardinalidades de dois conjuntos são iguais, eles são chamados de conjuntos equivalentes.

Example - se $A = \lbrace 1, 2, 6 \rbrace$ e $B = \lbrace 16, 17, 22 \rbrace$, eles são equivalentes, pois a cardinalidade de A é igual à cardinalidade de B. ie $|A| = |B| = 3$

Conjunto Sobreposto

Dois conjuntos que possuem pelo menos um elemento comum são chamados de conjuntos sobrepostos.

Em caso de conjuntos sobrepostos -

• $n(A \cup B) = n(A) + n(B) - n(A \cap B)$

• $n(A \cup B) = n(A - B) + n(B - A) + n(A \cap B)$

• $n(A) = n(A - B) + n(A \cap B)$

• $n(B) = n(B - A) + n(A \cap B)$

Example - Vamos, $A = \lbrace 1, 2, 6 \rbrace$ e $B = \lbrace 6, 12, 42 \rbrace$. Há um elemento comum '6', portanto, esses conjuntos são conjuntos sobrepostos.

Conjunto Disjunto

Dois conjuntos A e B são chamados de conjuntos disjuntos se não tiverem nem mesmo um elemento em comum. Portanto, os conjuntos separados têm as seguintes propriedades -

• $n(A \cap B) = \emptyset$

• $n(A \cup B) = n(A) + n(B)$

Example - Vamos, $A = \lbrace 1, 2, 6 \rbrace$ e $B = \lbrace 7, 9, 14 \rbrace$, não há um único elemento comum, portanto, esses conjuntos são conjuntos sobrepostos.

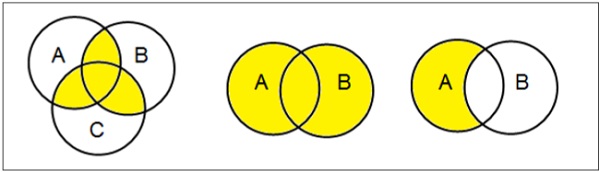
Diagramas venn

O diagrama de Venn, inventado em 1880 por John Venn, é um diagrama esquemático que mostra todas as relações lógicas possíveis entre diferentes conjuntos matemáticos.

Examples

Operações de conjunto

As operações de conjunto incluem União de conjuntos, Intersecção de conjuntos, Diferença de conjuntos, Complemento de conjunto e Produto cartesiano.

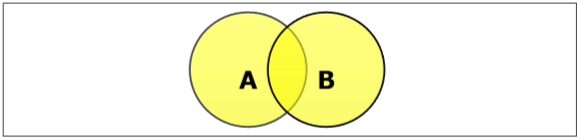
Definir União

A união dos conjuntos A e B (denotados por $A \cup B$) é o conjunto de elementos que estão em A, em B ou em A e B. Portanto, $A \cup B = \lbrace x \:| \: x \in A\ OR\ x \in B \rbrace$.

Example - se $A = \lbrace 10, 11, 12, 13 \rbrace$ e B = $\lbrace 13, 14, 15 \rbrace$, então $A \cup B = \lbrace 10, 11, 12, 13, 14, 15 \rbrace$. (O elemento comum ocorre apenas uma vez)

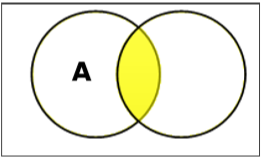
Definir interseção

A interseção dos conjuntos A e B (denotada por $A \cap B$) é o conjunto de elementos que estão em A e B. Portanto, $A \cap B = \lbrace x \:|\: x \in A\ AND\ x \in B \rbrace$.

Example - se $A = \lbrace 11, 12, 13 \rbrace$ e $B = \lbrace 13, 14, 15 \rbrace$, então $A \cap B = \lbrace 13 \rbrace$.

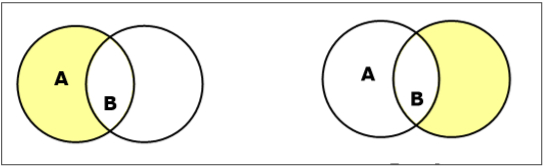
Definir Diferença / Complemento Relativo

A diferença de conjunto dos conjuntos A e B (denotada por $A – B$) é o conjunto de elementos que estão apenas em A, mas não em B. Portanto, $A - B = \lbrace x \:| \: x \in A\ AND\ x \notin B \rbrace$.

Example - se $A = \lbrace 10, 11, 12, 13 \rbrace$ e $B = \lbrace 13, 14, 15 \rbrace$, então $(A - B) = \lbrace 10, 11, 12 \rbrace$ e $(B - A) = \lbrace 14, 15 \rbrace$. Aqui podemos ver$(A - B) \ne (B - A)$

Complemento de um Conjunto

O complemento de um conjunto A (denotado por $A’$) é o conjunto de elementos que não estão no conjunto A. Portanto, $A' = \lbrace x | x \notin A \rbrace$.

Mais especificamente, $A'= (U - A)$ Onde $U$ é um conjunto universal que contém todos os objetos.

Example - se $A = \lbrace x \:| \: x\ \: {belongs\: to\: set\: of\: odd \:integers} \rbrace$ então $A' = \lbrace y\: | \: y\ \: {does\: not\: belong\: to\: set\: of\: odd\: integers } \rbrace$

Produto cartesiano / produto cruzado

O produto cartesiano de n número de conjuntos $A_1, A_2, \dots A_n$ denotado como $A_1 \times A_2 \dots \times A_n$ pode ser definido como todos os pares ordenados possíveis $(x_1, x_2, \dots x_n)$ Onde $x_1 \in A_1, x_2 \in A_2, \dots x_n \in A_n$

Example - Se pegarmos dois conjuntos $A = \lbrace a, b \rbrace$ e $B = \lbrace 1, 2 \rbrace$,

O produto cartesiano de A e B é escrito como - $A \times B = \lbrace (a, 1), (a, 2), (b, 1), (b, 2)\rbrace$

O produto cartesiano de B e A é escrito como - $B \times A = \lbrace (1, a), (1, b), (2, a), (2, b)\rbrace$

Conjunto de força

O conjunto de potência de um conjunto S é o conjunto de todos os subconjuntos de S, incluindo o conjunto vazio. A cardinalidade de um conjunto de potência de um conjunto S de cardinalidade n é$2^n$. Conjunto de potência é denotado como$P(S)$.

Example −

Para um conjunto $S = \lbrace a, b, c, d \rbrace$ vamos calcular os subconjuntos -

• Subconjuntos com 0 elementos - $\lbrace \emptyset \rbrace$ (o conjunto vazio)

• Subconjuntos com 1 elemento - $\lbrace a \rbrace, \lbrace b \rbrace, \lbrace c \rbrace, \lbrace d \rbrace$

• Subconjuntos com 2 elementos - $\lbrace a, b \rbrace, \lbrace a,c \rbrace, \lbrace a, d \rbrace, \lbrace b, c \rbrace, \lbrace b,d \rbrace,\lbrace c,d \rbrace$

• Subconjuntos com 3 elementos - $\lbrace a ,b, c\rbrace,\lbrace a, b, d \rbrace, \lbrace a,c,d \rbrace,\lbrace b,c,d \rbrace$

• Subconjuntos com 4 elementos - $\lbrace a, b, c, d \rbrace$

Conseqüentemente, $P(S)=$

$\lbrace \quad \lbrace \emptyset \rbrace, \lbrace a \rbrace, \lbrace b \rbrace, \lbrace c \rbrace, \lbrace d \rbrace, \lbrace a,b \rbrace, \lbrace a,c \rbrace, \lbrace a,d \rbrace, \lbrace b,c \rbrace, \lbrace b,d \rbrace, \lbrace c,d \rbrace, \lbrace a,b,c \rbrace, \lbrace a,b,d \rbrace, \lbrace a,c,d \rbrace, \lbrace b,c,d \rbrace, \lbrace a,b,c,d \rbrace \quad \rbrace$

$| P(S) | = 2^4 = 16$

Note - O conjunto de potência de um conjunto vazio também é um conjunto vazio.

$| P (\lbrace \emptyset \rbrace) | = 2^0 = 1$

Particionamento de um conjunto

A partição de um conjunto, digamos S , é uma coleção de n subconjuntos disjuntos, digamos$P_1, P_2, \dots P_n$ que satisfaça as três condições a seguir -

• $P_i$ não contém o conjunto vazio.

  $\lbrack P_i \ne \lbrace \emptyset \rbrace\ for\ all\ 0 \lt i \le n \rbrack$

• A união dos subconjuntos deve ser igual a todo o conjunto original.

  $\lbrack P_1 \cup P_2 \cup \dots \cup P_n = S \rbrack$

• A interseção de quaisquer dois conjuntos distintos está vazia.

  $\lbrack P_a \cap P_b = \lbrace \emptyset \rbrace,\ for\ a \ne b\ where\ n \ge a,\: b \ge 0 \rbrack$

Example

Deixei $S = \lbrace a, b, c, d, e, f, g, h \rbrace$

Um provável particionamento é $\lbrace a \rbrace, \lbrace b, c, d \rbrace, \lbrace e, f, g, h \rbrace$

Outro particionamento provável é $\lbrace a, b \rbrace, \lbrace c, d \rbrace, \lbrace e, f, g, h \rbrace$

Números de Sino

Os números das campainhas fornecem a contagem do número de maneiras de particionar um conjunto. Eles são denotados por$B_n$ onde n é a cardinalidade do conjunto.

Example -

Deixei $S = \lbrace 1, 2, 3\rbrace$, $n = |S| = 3$

As partições alternativas são -

1 $\emptyset , \lbrace 1, 2, 3 \rbrace$

2 $\lbrace 1 \rbrace , \lbrace 2, 3 \rbrace$

3 - $\lbrace 1, 2 \rbrace , \lbrace 3 \rbrace$

4 - $\lbrace 1, 3 \rbrace , \lbrace 2 \rbrace$

5 $\lbrace 1 \rbrace , \lbrace 2 \rbrace , \lbrace 3 \rbrace$

Conseqüentemente $B_3 = 5$

Sempre que os conjuntos estão sendo discutidos, a relação entre os elementos dos conjuntos é a próxima coisa que surge. Relations pode existir entre objetos do mesmo conjunto ou entre objetos de dois ou mais conjuntos.

Definição e Propriedades

Uma relação binária R do conjunto x a y (escrita como $xRy$ ou $R(x,y)$) é um subconjunto do produto cartesiano $x \times y$. Se o par ordenado de G for invertido, a relação também muda.

Geralmente uma relação n-ária R entre conjuntos $A_1, \dots ,\ and\ A_n$ é um subconjunto do produto n-ário $A_1 \times \dots \times A_n$. A cardinalidade mínima de uma relação R é Zero e a máxima é$n^2$ nesse caso.

Uma relação binária R em um único conjunto A é um subconjunto de $A \times A$.

Para dois conjuntos distintos, A e B, tendo cardinalidades m e n respectivamente, a cardinalidade máxima de uma relação R de A para B é mn .

Domínio e alcance

Se houver dois conjuntos A e B, e a relação R tiver par de ordem (x, y), então -

• o domain de R, Dom (R), é o conjunto $\lbrace x \:| \: (x, y) \in R \:for\: some\: y\: in\: B \rbrace$

• o range de R, Ran (R), é o conjunto $\lbrace y\: |\: (x, y) \in R \:for\: some\: x\: in\: A\rbrace$

Exemplos

Deixei, $A = \lbrace 1, 2, 9 \rbrace $ e $ B = \lbrace 1, 3, 7 \rbrace$

• Caso 1 - Se a relação R é 'igual a', então $R = \lbrace (1, 1), (3, 3) \rbrace$

  Dom (R) = $\lbrace 1, 3 \rbrace , Ran(R) = \lbrace 1, 3 \rbrace$

• Caso 2 - Se a relação R for 'menor que', então $R = \lbrace (1, 3), (1, 7), (2, 3), (2, 7) \rbrace$

  Dom (R) = $\lbrace 1, 2 \rbrace , Ran(R) = \lbrace 3, 7 \rbrace$

• Caso 3 - Se a relação R for 'maior que', então $R = \lbrace (2, 1), (9, 1), (9, 3), (9, 7) \rbrace$

  Dom (R) = $\lbrace 2, 9 \rbrace , Ran(R) = \lbrace 1, 3, 7 \rbrace$

Representação de relações usando gráfico

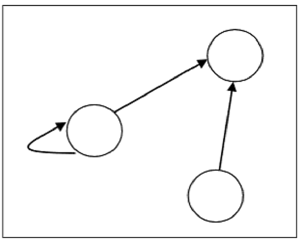
Uma relação pode ser representada usando um gráfico direcionado.

O número de vértices no gráfico é igual ao número de elementos no conjunto a partir do qual a relação foi definida. Para cada par ordenado (x, y) na relação R, haverá uma aresta direcionada do vértice 'x' ao vértice 'y'. Se houver um par ordenado (x, x), haverá auto-loop no vértice 'x'.

Suponha que haja uma relação $R = \lbrace (1, 1), (1,2), (3, 2) \rbrace$ no set $S = \lbrace 1, 2, 3 \rbrace$, pode ser representado pelo seguinte gráfico -

Tipos de Relações

• o Empty Relation entre os conjuntos X e Y, ou em E, é o conjunto vazio $\emptyset$

• o Full Relation entre os conjuntos X e Y é o conjunto $X \times Y$

• o Identity Relation no set X é o set $\lbrace (x, x) | x \in X \rbrace$

• A relação inversa R 'de uma relação R é definida como - $R' = \lbrace (b, a) | (a, b) \in R \rbrace$

  Example - se $R = \lbrace (1, 2), (2, 3) \rbrace$ então $R' $ será $\lbrace (2, 1), (3, 2) \rbrace$

• Uma relação R no conjunto A é chamada Reflexive E se $\forall a \in A$ está relacionado a um (aRa mantém)

  Example - A relação $R = \lbrace (a, a), (b, b) \rbrace$ no set $X = \lbrace a, b \rbrace$ é reflexivo.

• Uma relação R no conjunto A é chamada Irreflexive se não $a \in A$ está relacionado com a (aRa não se mantém).

  Example - A relação $R = \lbrace (a, b), (b, a) \rbrace$ no set $X = \lbrace a, b \rbrace$ é irreflexivo.

• Uma relação R no conjunto A é chamada Symmetric E se $xRy$ implica $yRx$, $\forall x \in A$ e $\forall y \in A$.

  Example - A relação $R = \lbrace (1, 2), (2, 1), (3, 2), (2, 3) \rbrace$ no set $A = \lbrace 1, 2, 3 \rbrace$ é simétrico.

• Uma relação R no conjunto A é chamada Anti-Symmetric E se $xRy$ e $yRx$ implica $x = y \: \forall x \in A$ e $\forall y \in A$.

  Example - A relação $R = \lbrace (x, y)\to N |\:x \leq y \rbrace$ é anti-simétrico desde $x \leq y$ e $y \leq x$ implica $x = y$.

• Uma relação R no conjunto A é chamada Transitive E se $xRy$ e $yRz$ implica $xRz, \forall x,y,z \in A$.

  Example - A relação $R = \lbrace (1, 2), (2, 3), (1, 3) \rbrace$ no set $A = \lbrace 1, 2, 3 \rbrace$ é transitivo.

• Uma relação é um Equivalence Relation se for reflexivo, simétrico e transitivo.

  Example - A relação $R = \lbrace (1, 1), (2, 2), (3, 3), (1, 2), (2,1), (2,3), (3,2), (1,3), (3,1) \rbrace$ no set $A = \lbrace 1, 2, 3 \rbrace$ é uma relação de equivalência, pois é reflexiva, simétrica e transitiva.

UMA Functionatribui a cada elemento de um conjunto, exatamente um elemento de um conjunto relacionado. As funções encontram sua aplicação em vários campos, como representação da complexidade computacional de algoritmos, objetos de contagem, estudo de sequências e strings, para citar alguns. O terceiro e último capítulo desta parte destaca os aspectos importantes das funções.

Função - Definição

Uma função ou mapeamento (definido como $f: X \rightarrow Y$) é um relacionamento de elementos de um conjunto X com elementos de outro conjunto Y (X e Y são conjuntos não vazios). X é denominado Domínio e Y é denominado Codomain da função 'f'.

Função 'f' é uma relação em X e Y tal que para cada $x \in X$, existe um único $y \in Y$ de tal modo que $(x,y) \in R$. 'x' é chamado de pré-imagem e 'y' é chamado de imagem da função f.

Uma função pode ser um para um ou muitos para um, mas não um para muitos.

Função injetiva / um-para-um

Uma função $f: A \rightarrow B$ é injetiva ou função um a um se para cada $b \in B$, existe no máximo um $a \in A$ de tal modo que $f(s) = t$.

Isso significa uma função f é injetivo se $a_1 \ne a_2$ implica $f(a1) \ne f(a2)$.

Exemplo

• $f: N \rightarrow N, f(x) = 5x$ é injetivo.

• $f: N \rightarrow N, f(x) = x^2$ é injetivo.

• $f: R\rightarrow R, f(x) = x^2$ não é injetivo como $(-x)^2 = x^2$

Função Surjetiva / Onto

Uma função $f: A \rightarrow B$é sobrejetiva (em) se a imagem de f for igual ao seu alcance. Equivalentemente, para cada$b \in B$, existe algum $a \in A$ de tal modo que $f(a) = b$. Isso significa que para qualquer y em B, existe algum x em A tal que$y = f(x)$.

Exemplo

• $f : N \rightarrow N, f(x) = x + 2$ é sobrejetora.

• $f : R \rightarrow R, f(x) = x^2$ não é sobrejetora, pois não podemos encontrar um número real cujo quadrado seja negativo.

Bijetivo / Correspondente Um-para-um

Uma função $f: A \rightarrow B$ é bijetivo ou um a um correspondente se e somente se f é injetiva e sobrejetiva.

Problema

Prove que é uma função $f: R \rightarrow R$ definido por $f(x) = 2x – 3$ é uma função bijetiva.

Explanation - Temos que provar que essa função é tanto injetiva quanto sobrejetora.

E se $f(x_1) = f(x_2)$, então $2x_1 – 3 = 2x_2 – 3 $ e isso implica que $x_1 = x_2$.

Portanto, f é injective.

Aqui, $2x – 3= y$

Então, $x = (y+5)/3$ que pertence a R e $f(x) = y$.

Portanto, f é surjective.

Desde a f são ambos surjective e injective, nós podemos dizer f é bijective.

Inverso de uma função

o inverse de uma função correspondente um-para-um $f : A \rightarrow B$, é a função $g : B \rightarrow A$, mantendo a seguinte propriedade -

$f(x) = y \Leftrightarrow g(y) = x$

A função f é chamada invertible, se sua função inversa g existe.

Exemplo

• Uma função $f : Z \rightarrow Z, f(x)=x+5$, é invertível, pois tem a função inversa $ g : Z \rightarrow Z, g(x)= x-5$.

• Uma função $f : Z \rightarrow Z, f(x)=x^2$ não é invertível, pois não é um para um como $(-x)^2=x^2$.

Composição de Funções

Duas funções $f: A \rightarrow B$ e $g: B \rightarrow C$ pode ser composto para dar uma composição $g o f$. Esta é uma função de A a C definida por$(gof)(x) = g(f(x))$

Exemplo

Deixei $f(x) = x + 2$ e $g(x) = 2x + 1$, encontrar $( f o g)(x)$ e $( g o f)(x)$.

Solução

$(f o g)(x) = f (g(x)) = f(2x + 1) = 2x + 1 + 2 = 2x + 3$

$(g o f)(x) = g (f(x)) = g(x + 2) = 2 (x+2) + 1 = 2x + 5$

Conseqüentemente, $(f o g)(x) \neq (g o f)(x)$

Alguns fatos sobre composição

• Se feg são um-para-um, então a função $(g o f)$ também é um para um.

• Se f e g estiverem ativados, a função $(g o f)$ também está ligado.

• A composição sempre possui propriedade associativa, mas não possui propriedade comutativa.

As regras da lógica matemática especificam métodos de raciocínio de afirmações matemáticas. O filósofo grego Aristóteles foi o pioneiro do raciocínio lógico. O raciocínio lógico fornece a base teórica para muitas áreas da matemática e, consequentemente, da ciência da computação. Tem muitas aplicações práticas em ciência da computação, como design de máquinas de computação, inteligência artificial, definição de estruturas de dados para linguagens de programação, etc.

Propositional Logicpreocupa-se com afirmações às quais os valores de verdade, “verdadeiro” e “falso”, podem ser atribuídos. O objetivo é analisar essas afirmações individualmente ou de forma composta.

Lógica Preposicional - Definição

Uma proposição é uma coleção de declarações declarativas que têm um valor de verdade "verdadeiro" ou um valor de verdade "falso". Uma proposição consiste em variáveis ​​proposicionais e conectivos. Denotamos as variáveis ​​proposicionais por letras maiúsculas (A, B, etc). Os conectivos conectam as variáveis ​​proposicionais.

Alguns exemplos de proposições são fornecidos abaixo -

• "Man is Mortal", retorna o valor de verdade “TRUE”
• "12 + 9 = 3 - 2", retorna o valor verdadeiro “FALSO”

O seguinte não é uma proposição -

• "A é menor que 2". É porque, a menos que forneçamos um valor específico de A, não podemos dizer se a afirmação é verdadeira ou falsa.

Conectivos

Na lógica proposicional, geralmente usamos cinco conectivos que são -

• OR ($\lor$)

• E ($\land$)

• Negação / NÃO ($\lnot$)

• Implicação / se-então ($\rightarrow$)

• Se e apenas se ($\Leftrightarrow$)

OR ($\lor$) - A operação OR de duas proposições A e B (escritas como $A \lor B$) é verdadeiro se pelo menos qualquer uma das variáveis ​​proposicionais A ou B for verdadeira.

A tabela de verdade é a seguinte -

UMA	B	A ∨ B
Verdadeiro	Verdadeiro	Verdadeiro
Verdadeiro	Falso	Verdadeiro
Falso	Verdadeiro	Verdadeiro
Falso	Falso	Falso

AND ($\land$) - A operação AND de duas proposições A e B (escritas como $A \land B$) é verdadeiro se ambas as variáveis ​​proposicionais A e B são verdadeiras.

A tabela de verdade é a seguinte -

UMA	B	A ∧ B
Verdadeiro	Verdadeiro	Verdadeiro
Verdadeiro	Falso	Falso
Falso	Verdadeiro	Falso
Falso	Falso	Falso

Negation ($\lnot$) - A negação de uma proposição A (escrita como $\lnot A$) é falso quando A é verdadeiro e é verdadeiro quando A é falso.

A tabela de verdade é a seguinte -

UMA	¬ A
Verdadeiro	Falso
Falso	Verdadeiro

Implication / if-then ($\rightarrow$) - Uma implicação $A \rightarrow B$é a proposição “se A, então B”. É falso se A for verdadeiro e B for falso. Os demais casos são verdadeiros.

A tabela de verdade é a seguinte -

UMA	B	A → B
Verdadeiro	Verdadeiro	Verdadeiro
Verdadeiro	Falso	Falso
Falso	Verdadeiro	Verdadeiro
Falso	Falso	Verdadeiro

If and only if ($ \Leftrightarrow $) - $A \Leftrightarrow B$ é o conectivo lógico bi-condicional que é verdadeiro quando peq são iguais, ou seja, ambos são falsos ou ambos são verdadeiros.

A tabela de verdade é a seguinte -

UMA	B	A ⇔ B
Verdadeiro	Verdadeiro	Verdadeiro
Verdadeiro	Falso	Falso
Falso	Verdadeiro	Falso
Falso	Falso	Verdadeiro

Tautologias

Uma tautologia é uma fórmula que é sempre verdadeira para todos os valores de suas variáveis ​​proposicionais.

Example - Prove $\lbrack (A \rightarrow B) \land A \rbrack \rightarrow B$ é uma tautologia

A tabela de verdade é a seguinte -

UMA	B	A → B	(A → B) ∧ A	[(A → B) ∧ A] → B
Verdadeiro	Verdadeiro	Verdadeiro	Verdadeiro	Verdadeiro
Verdadeiro	Falso	Falso	Falso	Verdadeiro
Falso	Verdadeiro	Verdadeiro	Falso	Verdadeiro
Falso	Falso	Verdadeiro	Falso	Verdadeiro

Como podemos ver todos os valores de $\lbrack (A \rightarrow B) \land A \rbrack \rightarrow B$ é "Verdadeiro", é uma tautologia.

Contradições

Uma Contradição é uma fórmula que é sempre falsa para cada valor de suas variáveis ​​proposicionais.

Example - Prove $(A \lor B) \land \lbrack ( \lnot A) \land (\lnot B) \rbrack$ é uma contradição

A tabela de verdade é a seguinte -

UMA	B	A ∨ B	¬ A	¬ B	(¬ A) ∧ (¬ B)	(A ∨ B) ∧ [(¬ A) ∧ (¬ B)]
Verdadeiro	Verdadeiro	Verdadeiro	Falso	Falso	Falso	Falso
Verdadeiro	Falso	Verdadeiro	Falso	Verdadeiro	Falso	Falso
Falso	Verdadeiro	Verdadeiro	Verdadeiro	Falso	Falso	Falso
Falso	Falso	Falso	Verdadeiro	Verdadeiro	Verdadeiro	Falso

Como podemos ver todos os valores de $(A \lor B) \land \lbrack ( \lnot A) \land (\lnot B) \rbrack$ é “False”, é uma contradição.

Contingência

Uma contingência é uma fórmula que tem alguns valores verdadeiros e falsos para cada valor de suas variáveis ​​proposicionais.

Example - Prove $(A \lor B) \land (\lnot A)$ uma contingência

A tabela de verdade é a seguinte -

UMA	B	A ∨ B	¬ A	(A ∨ B) ∧ (¬ A)
Verdadeiro	Verdadeiro	Verdadeiro	Falso	Falso
Verdadeiro	Falso	Verdadeiro	Falso	Falso
Falso	Verdadeiro	Verdadeiro	Verdadeiro	Verdadeiro
Falso	Falso	Falso	Verdadeiro	Falso

Como podemos ver todos os valores de $(A \lor B) \land (\lnot A)$ tem “Verdadeiro” e “Falso”, é uma contingência.

Equivalências proposicionais

Duas declarações X e Y são logicamente equivalentes se qualquer uma das seguintes condições for mantida -

• As tabelas de verdade de cada afirmação têm os mesmos valores de verdade.

• A declaração bi-condicional $X \Leftrightarrow Y$ é uma tautologia.

Example - Prove $\lnot (A \lor B) and \lbrack (\lnot A) \land (\lnot B) \rbrack$ são equivalentes

Teste pelo ^1º método (tabela de verdade de correspondência)

UMA	B	A ∨ B	¬ (A ∨ B)	¬ A	¬ B	[(¬ A) ∧ (¬ B)]
Verdadeiro	Verdadeiro	Verdadeiro	Falso	Falso	Falso	Falso
Verdadeiro	Falso	Verdadeiro	Falso	Falso	Verdadeiro	Falso
Falso	Verdadeiro	Verdadeiro	Falso	Verdadeiro	Falso	Falso
Falso	Falso	Falso	Verdadeiro	Verdadeiro	Verdadeiro	Verdadeiro

Aqui, podemos ver os valores verdadeiros de $\lnot (A \lor B) and \lbrack (\lnot A) \land (\lnot B) \rbrack$ são iguais, portanto, as declarações são equivalentes.

Teste pelo ^2º método (Bi-condicionalidade)

UMA	B	¬ (A ∨ B)	[(¬ A) ∧ (¬ B)]	[¬ (A ∨ B)] ⇔ [(¬ A) ∧ (¬ B)]
Verdadeiro	Verdadeiro	Falso	Falso	Verdadeiro
Verdadeiro	Falso	Falso	Falso	Verdadeiro
Falso	Verdadeiro	Falso	Falso	Verdadeiro
Falso	Falso	Verdadeiro	Verdadeiro	Verdadeiro

Como $\lbrack \lnot (A \lor B) \rbrack \Leftrightarrow \lbrack (\lnot A ) \land (\lnot B) \rbrack$ é uma tautologia, as declarações são equivalentes.

Inverso, Converse e Contra-positivo

Implicação / se-então $(\rightarrow)$também é chamada de declaração condicional. Tem duas partes -

• Hipótese, p
• Conclusão, q

Conforme mencionado anteriormente, é denotado como $p \rightarrow q$.

Example of Conditional Statement- “Se você fizer sua lição de casa, você não será punido.” Aqui, "você faz sua lição de casa" é a hipótese, p, e "você não será punido" é a conclusão, q.

Inverse- O inverso da afirmação condicional é a negação da hipótese e da conclusão. Se a declaração for “Se p, então q”, o inverso será “Se não p, então não q”. Assim, o inverso de$p \rightarrow q$ é $ \lnot p \rightarrow \lnot q$.

Example - O inverso de “Se você fizer sua lição de casa, você não será punido” é “Se você não fizer sua lição de casa, você será punido”.

Converse- O inverso da declaração condicional é calculado trocando a hipótese e a conclusão. Se a declaração for “Se p, então q”, o inverso será “Se q, então p”. O inverso de$p \rightarrow q$ é $q \rightarrow p$.

Example - O inverso de “Se você fizer sua lição de casa, você não será punido” é “Se você não for punido, você faz sua lição de casa”.

Contra-positive- O contra-positivo da condicional é calculado trocando a hipótese e a conclusão da afirmação inversa. Se a afirmação for “Se p, então q”, o contra-positivo será “Se não q, então não p”. O contra-positivo de$p \rightarrow q$ é $\lnot q \rightarrow \lnot p$.

Example - O Contra-positivo de “Se você fizer sua lição de casa, não será punido” é “Se você for punido, você não fez sua lição de casa”.

Princípio da Dualidade

O princípio da dualidade afirma que, para qualquer afirmação verdadeira, a afirmação dual obtida trocando uniões em interseções (e vice-versa) e trocando conjunto universal por conjunto nulo (e vice-versa) também é verdadeira. Se dual de qualquer afirmação for a própria afirmação, é ditoself-dual declaração.

Example - O dual de $(A \cap B ) \cup C$ é $(A \cup B) \cap C$

Formas normais

Podemos converter qualquer proposição em duas formas normais -

• Forma normal conjuntiva
• Forma normal disjuntiva

Forma normal conjuntiva

Um enunciado composto está na forma normal conjuntiva se for obtido operando AND entre variáveis ​​(negação de variáveis ​​incluídas) conectadas com ORs. Em termos de operações de conjunto, é um enunciado composto obtido por Intersecção entre variáveis ​​relacionadas com Sindicatos.

Examples

• $(A \lor B) \land (A \lor C) \land (B \lor C \lor D)$

• $(P \cup Q) \cap (Q \cup R)$

Forma Normal Disjuntiva

Uma declaração composta está na forma normal disjuntiva se for obtida operando OR entre variáveis ​​(negação de variáveis ​​incluídas) conectadas com ANDs. Em termos de operações de conjunto, é uma declaração composta obtida por Union entre variáveis ​​conectadas com Intersecções.

Examples

• $(A \land B) \lor (A \land C) \lor (B \land C \land D)$

• $(P \cap Q) \cup (Q \cap R)$

Predicate Logic lida com predicados, que são proposições contendo variáveis.

Lógica de Predicado - Definição

Um predicado é uma expressão de uma ou mais variáveis ​​definidas em algum domínio específico. Um predicado com variáveis ​​pode ser proposto atribuindo um valor à variável ou quantificando a variável.

A seguir estão alguns exemplos de predicados -

• Deixe E (x, y) denotar "x = y"
• Deixe X (a, b, c) denotar "a + b + c = 0"
• Deixe M (x, y) denotar "x é casado com y"

Fórmula Bem Formada

Well Formed Formula (wff) é um predicado contendo qualquer um dos seguintes -

• Todas as constantes e variáveis ​​proposicionais são wffs

• Se x é uma variável e Y é um wff, $\forall x Y$ e $\exists x Y$ também são wff

• O valor verdadeiro e os valores falsos são wffs

• Cada fórmula atômica é um wff

• Todos os conectivos conectando wffs são wffs

Quantificadores

A variável dos predicados é quantificada por quantificadores. Existem dois tipos de quantificador na lógica de predicado - Quantificador Universal e Quantificador Existencial.

Quantificador Universal

O quantificador universal afirma que as afirmações dentro de seu escopo são verdadeiras para cada valor da variável específica. É denotado pelo símbolo$\forall$.

$\forall x P(x)$ é lido como para cada valor de x, P (x) é verdadeiro.

Example - "O homem é mortal" pode ser transformado na forma proposicional $\forall x P(x)$ onde P (x) é o predicado que denota x é mortal e o universo do discurso são todos os homens.

Quantificador Existencial

O quantificador existencial afirma que as afirmações dentro de seu escopo são verdadeiras para alguns valores da variável específica. É denotado pelo símbolo$\exists $.

$\exists x P(x)$ é lido como para alguns valores de x, P (x) é verdadeiro.

Example - "Algumas pessoas são desonestas" pode ser transformado na forma proposicional $\exists x P(x)$ onde P (x) é o predicado que denota que x é desonesto e o universo do discurso são algumas pessoas.

Quantificadores Aninhados

Se usarmos um quantificador que aparece no escopo de outro quantificador, ele é chamado de quantificador aninhado.

Example

• $\forall\ a\: \exists b\: P (x, y)$ Onde $P (a, b)$ denota $a + b = 0$

• $\forall\ a\: \forall\: b\: \forall\: c\: P (a, b, c)$ Onde $P (a, b)$ denota $a + (b + c) = (a + b) + c$

Note - $\forall\: a\: \exists b\: P (x, y) \ne \exists a\: \forall b\: P (x, y)$

Para deduzir novas afirmações das afirmações cuja verdade já conhecemos, Rules of Inference são usados.

Para que servem as regras de inferência?

A lógica matemática é freqüentemente usada para provas lógicas. Provas são argumentos válidos que determinam os valores verdadeiros de afirmações matemáticas.

Um argumento é uma sequência de declarações. A última declaração é a conclusão e todas as suas declarações anteriores são chamadas de premissas (ou hipótese). O símbolo "$\therefore$”, (Leia-se, portanto) é colocado antes da conclusão. Um argumento válido é aquele em que a conclusão decorre dos valores de verdade das premissas.

As regras de inferência fornecem os modelos ou diretrizes para construir argumentos válidos a partir das declarações que já temos.

Tabela de regras de inferência

Regra de Inferência	Nome	Regra de Inferência	Nome
$$\begin{matrix} P \\ \hline \therefore P \lor Q \end{matrix}$$	Adição	$$\begin{matrix} P \lor Q \\ \lnot P \\ \hline \therefore Q \end{matrix}$$	Silogismo Disjuntivo
$$\begin{matrix} P \\ Q \\ \hline \therefore P \land Q \end{matrix}$$	Conjunção	$$\begin{matrix} P \rightarrow Q \\ Q \rightarrow R \\ \hline \therefore P \rightarrow R \end{matrix}$$	Silogismo hipotético
$$\begin{matrix} P \land Q\\ \hline \therefore P \end{matrix}$$	Simplificação	$$\begin{matrix} ( P \rightarrow Q ) \land (R \rightarrow S) \\ P \lor R \\ \hline \therefore Q \lor S \end{matrix}$$	Dilema Construtivo
$$\begin{matrix} P \rightarrow Q \\ P \\ \hline \therefore Q \end{matrix}$$	Modus ponens	$$\begin{matrix} (P \rightarrow Q) \land (R \rightarrow S) \\ \lnot Q \lor \lnot S \\ \hline \therefore \lnot P \lor \lnot R \end{matrix}$$	Dilema Destrutivo
$$\begin{matrix} P \rightarrow Q \\ \lnot Q \\ \hline \therefore \lnot P \end{matrix}$$	Modus Tollens

Adição

Se P é uma premissa, podemos usar a regra de adição para derivar $ P \lor Q $.

$$\begin{matrix} P \\ \hline \therefore P \lor Q \end{matrix}$$

Exemplo

Seja P a proposição, "Ele estuda muito" é verdade

Portanto - "Ou ele estuda muito ou é um péssimo aluno." Aqui, Q é a proposição “ele é um péssimo aluno”.

Conjunção

Se P e Q são duas premissas, podemos usar a regra de conjunção para derivar $ P \land Q $.

$$\begin{matrix} P \\ Q \\ \hline \therefore P \land Q \end{matrix}$$

Exemplo

Vamos P - “Ele estuda muito”

Let Q - “Ele é o melhor menino da classe”

Portanto - "Ele estuda muito e é o melhor menino da classe"

Simplificação

E se $P \land Q$ é uma premissa, podemos usar a regra de simplificação para derivar P.

$$\begin{matrix} P \land Q\\ \hline \therefore P \end{matrix}$$

Exemplo

“Ele estuda muito e é o melhor menino da classe”, $P \land Q$

Portanto - "Ele estuda muito"

Modus ponens

Se P e $P \rightarrow Q$ são duas premissas, podemos usar o Modus Ponens para derivar Q.

$$\begin{matrix} P \rightarrow Q \\ P \\ \hline \therefore Q \end{matrix}$$

Exemplo

“Se você tem uma senha, pode entrar no Facebook”, $P \rightarrow Q$

"Você tem uma senha", P

Portanto - "Você pode fazer logon no Facebook"

Modus Tollens

E se $P \rightarrow Q$ e $\lnot Q$ são duas premissas, podemos usar o Modus Tollens para derivar $\lnot P$.

$$\begin{matrix} P \rightarrow Q \\ \lnot Q \\ \hline \therefore \lnot P \end{matrix}$$

Exemplo

“Se você tem uma senha, pode entrar no Facebook”, $P \rightarrow Q$

"Você não pode entrar no Facebook", $\lnot Q$

Portanto - "Você não tem uma senha"

Silogismo Disjuntivo

E se $\lnot P$ e $P \lor Q$ são duas premissas, podemos usar o silogismo disjuntivo para derivar Q.

$$\begin{matrix} \lnot P \\ P \lor Q \\ \hline \therefore Q \end{matrix}$$

Exemplo

“O sorvete não tem sabor de baunilha”, $\lnot P$

"O sorvete é com sabor de baunilha ou com sabor de chocolate", $P \lor Q$

Portanto - “O sorvete tem sabor de chocolate”

Silogismo hipotético

E se $P \rightarrow Q$ e $Q \rightarrow R$ são duas premissas, podemos usar o silogismo hipotético para derivar $P \rightarrow R$

$$\begin{matrix} P \rightarrow Q \\ Q \rightarrow R \\ \hline \therefore P \rightarrow R \end{matrix}$$

Exemplo

“Se chover não irei à escola”, $P \rightarrow Q$

“Se eu não for para a escola, não vou precisar fazer lição de casa”, $Q \rightarrow R$

Portanto - "Se chover, não vou precisar fazer lição de casa"

Dilema Construtivo

E se $( P \rightarrow Q ) \land (R \rightarrow S)$ e $P \lor R$ são duas premissas, podemos usar o dilema construtivo para derivar $Q \lor S$.

$$\begin{matrix} ( P \rightarrow Q ) \land (R \rightarrow S) \\ P \lor R \\ \hline \therefore Q \lor S \end{matrix}$$

Exemplo

“Se chover, vou me despedir”, $( P \rightarrow Q )$

“Se estiver calor lá fora, vou tomar banho”, $(R \rightarrow S)$

“Ou vai chover ou está calor lá fora”, $P \lor R$

Portanto - "Vou me despedir ou vou tomar um banho"

Dilema Destrutivo

E se $(P \rightarrow Q) \land (R \rightarrow S)$ e $ \lnot Q \lor \lnot S $ são duas premissas, podemos usar o dilema destrutivo para derivar $\lnot P \lor \lnot R$.

$$\begin{matrix} (P \rightarrow Q) \land (R \rightarrow S) \\ \lnot Q \lor \lnot S \\ \hline \therefore \lnot P \lor \lnot R \end{matrix}$$

Exemplo

“Se chover, vou me despedir”, $(P \rightarrow Q )$

“Se estiver calor lá fora, vou tomar banho”, $(R \rightarrow S)$

“Ou não vou me despedir ou não vou tomar banho”, $\lnot Q \lor \lnot S$

Portanto - "Ou não chove ou não faz calor lá fora"

A Teoria dos Grupos é um ramo da matemática e da álgebra abstrata que define uma estrutura algébrica denominada group. Geralmente, um grupo é composto por um conjunto de elementos e uma operação sobre quaisquer dois elementos nesse conjunto para formar um terceiro elemento também nesse conjunto.

Em 1854, Arthur Cayley, o matemático britânico, deu a definição moderna de grupo pela primeira vez -

“Um conjunto de símbolos todos diferentes, e tal que o produto de quaisquer dois deles (não importa em que ordem), ou o produto de qualquer um deles em si mesmo, pertence ao conjunto, é considerado um grupo . Esses símbolos não são em geral conversíveis [comutativos], mas são associativos. ”

Neste capítulo, saberemos sobre operators and postulates que formam os fundamentos da teoria dos conjuntos, teoria dos grupos e álgebra booleana.

Qualquer conjunto de elementos em um sistema matemático pode ser definido com um conjunto de operadores e uma série de postulados.

UMA binary operatordefinida em um conjunto de elementos é uma regra que atribui a cada par de elementos um elemento exclusivo desse conjunto. Por exemplo, dado o conjunto$ A = \lbrace 1, 2, 3, 4, 5 \rbrace $, nós podemos dizer $\otimes$ é um operador binário para a operação $c = a \otimes b$, if it specifies a rule for finding c for the pair of $(a,b)$, such that $a,b,c \in A$.

The postulates of a mathematical system form the basic assumptions from which rules can be deduced. The postulates are −

Closure

A set is closed with respect to a binary operator if for every pair of elements in the set, the operator finds a unique element from that set.

Example

Let $A = \lbrace 0, 1, 2, 3, 4, 5, \dots \rbrace$

This set is closed under binary operator into $(\ast)$, because for the operation $c = a \ast b$, for any $a, b \in A$, the product $c \in A$.

The set is not closed under binary operator divide $(\div)$, because, for the operation $c = a \div b$, for any $a, b \in A$, the product c may not be in the set A. If $a = 7, b = 2$, then $c = 3.5$. Here $a,b \in A$ but $c \notin A$.

Associative Laws

A binary operator $\otimes$ on a set A is associative when it holds the following property −

$(x \otimes y) \otimes z = x \otimes (y \otimes z)$, where $x, y, z \in A $

Example

Let $A = \lbrace 1, 2, 3, 4 \rbrace$

The operator plus $( + )$ is associative because for any three elements, $x,y,z \in A$, the property $(x + y) + z = x + ( y + z )$ holds.

The operator minus $( - )$ is not associative since

$$( x - y ) - z \ne x - ( y - z )$$

Commutative Laws

A binary operator $\otimes$ on a set A is commutative when it holds the following property −

$x \otimes y = y \otimes x$, Onde $x, y \in A$

Exemplo

Deixei $A = \lbrace 1, 2, 3, 4 \rbrace$

O operador mais $( + )$ é comutativo porque para quaisquer dois elementos, $x,y \in A$, a propriedade $x + y = y + x$ detém.

O operador menos $( - )$ não é associativo desde

$$x - y \ne y - x$$

Leis distributivas

Dois operadores binários $\otimes$ e $\circledast$ em um conjunto A, são distributivos sobre o operador $\circledast$ quando a seguinte propriedade é válida -

$x \otimes (y \circledast z) = (x \otimes y) \circledast (x \otimes z)$, Onde $x, y, z \in A $

Exemplo

Deixei $A = \lbrace 1, 2, 3, 4 \rbrace$

Os operadores em $( * )$ e mais $( + )$ são distributivos sobre o operador + porque para quaisquer três elementos, $x,y,z \in A$, a propriedade $x * ( y + z ) = ( x * y ) + ( x * z )$ detém.

No entanto, esses operadores não são distributivos ao longo $*$ Desde a

$$x + ( y * z ) \ne ( x + y ) * ( x + z )$$

Elemento de Identidade

Um conjunto A tem um elemento de identidade em relação a uma operação binária $\otimes$ em A, se houver um elemento $e \in A$, de modo que a seguinte propriedade seja válida -

$e \otimes x = x \otimes e$, Onde $x \in A$

Exemplo

Deixei $Z = \lbrace 0, 1, 2, 3, 4, 5, \dots \rbrace$

O elemento 1 é um elemento de identidade em relação à operação $*$ já que para qualquer elemento $x \in Z$,

$$1 * x = x * 1$$

Por outro lado, não há elemento de identidade para a operação menos $( - )$

Inverso

Se um conjunto A tiver um elemento de identidade $e$ com respeito a um operador binário $\otimes $, é dito ter um inverso sempre que para cada elemento $x \in A$, existe outro elemento $y \in A$, de modo que a seguinte propriedade seja válida -

$$x \otimes y = e$$

Exemplo

Deixei $A = \lbrace \dots -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, \dots \rbrace$

Dada a operação plus $( + )$ e $e = 0$, o inverso de qualquer elemento x é $(-x)$ Desde a $x + (x) = 0$

Lei De Morgan

As Leis de De Morgan fornecem um par de transformações entre união e interseção de dois (ou mais) conjuntos em termos de seus complementos. As leis são -

$$(A \cup B)' = A' \cap B'$$

$$(A \cap B)' = A' \cup B'$$

Exemplo

Deixei $A = \lbrace 1, 2, 3, 4 \rbrace ,B = \lbrace 1, 3, 5, 7 \rbrace$, e

Conjunto universal $U = \lbrace 1, 2, 3, \dots, 9, 10 \rbrace$

$A' = \lbrace 5, 6, 7, 8, 9, 10 \rbrace$

$B' = \lbrace 2, 4, 6, 8, 9, 10 \rbrace$

$A \cup B = \lbrace 1, 2, 3, 4, 5, 7 \rbrace$

$A \cap B = \lbrace 1, 3 \rbrace $

$(A \cup B)' = \lbrace 6, 8, 9, 10 \rbrace$

$A' \cap B' = \lbrace 6, 8, 9, 10 \rbrace$

Assim, vemos que $(A \cup B)' = A' \cap B'$

$(A \cap B)' = \lbrace 2, 4, 5, 6, 7, 8, 9, 10 \rbrace$

$A' \cup B' = \lbrace 2, 4, 5, 6, 7, 8, 9, 10 \rbrace$

Assim, vemos que $(A \cap B)' = A' \cup B'$

Semigrupo

Um conjunto finito ou infinito $‘S’$ com uma operação binária $‘\omicron’$ (Composição) é chamado de semigrupo se ele se mantiver seguindo duas condições simultaneamente -

• Closure - Para cada par $(a, b) \in S, \:(a \omicron b)$ tem que estar presente no set $S$.

• Associative - Para cada elemento $a, b, c \in S, (a \omicron b) \omicron c = a \omicron (b \omicron c)$ deve esperar.

Exemplo

O conjunto de inteiros positivos (excluindo zero) com operação de adição é um semigrupo. Por exemplo,$ S = \lbrace 1, 2, 3, \dots \rbrace $

Aqui, a propriedade de fechamento é válida para cada par $(a, b) \in S, (a + b)$ está presente no conjunto S. Por exemplo, $1 + 2 = 3 \in S]$

A propriedade associativa também é válida para todos os elementos $a, b, c \in S, (a + b) + c = a + (b + c)$. Por exemplo,$(1 + 2) + 3 = 1 + (2 + 3) = 5$

Monóide

Um monóide é um semigrupo com um elemento de identidade. O elemento de identidade (denotado por$e$ ou E) de um conjunto S é um elemento tal que $(a \omicron e) = a$, para cada elemento $a \in S$. Um elemento de identidade também é chamado deunit element. Então, um monóide possui três propriedades simultaneamente -Closure, Associative, Identity element.

Exemplo

O conjunto de inteiros positivos (excluindo zero) com operação de multiplicação é um monóide. $S = \lbrace 1, 2, 3, \dots \rbrace $

Aqui, a propriedade de fechamento é válida para cada par $(a, b) \in S, (a \times b)$ está presente no conjunto S. [Por exemplo, $1 \times 2 = 2 \in S$ e assim por diante]

A propriedade associativa também é válida para todos os elementos $a, b, c \in S, (a \times b) \times c = a \times (b \times c)$ [Por exemplo, $(1 \times 2) \times 3 = 1 \times (2 \times 3) = 6$ e assim por diante]

A propriedade de identidade também é válida para todos os elementos $a \in S, (a \times e) = a$ [Por exemplo, $(2 \times 1) = 2, (3 \times 1) = 3$e assim por diante]. Aqui, o elemento de identidade é 1.

Grupo

Um grupo é um monóide com um elemento inverso. O elemento inverso (denotado por I) de um conjunto S é um elemento tal que$(a \omicron I) = (I \omicron a) = a$, para cada elemento $a \in S$. Assim, um grupo possui quatro propriedades simultaneamente - i) Fechamento, ii) Associativo, iii) Elemento de identidade, iv) Elemento inverso. A ordem de um grupo G é o número de elementos em G e a ordem de um elemento em um grupo é o número inteiro menos positivo n, de modo que an é o elemento de identidade desse grupo G.

Exemplos

O conjunto de $N \times N$ matrizes não singulares formam um grupo sob a operação de multiplicação de matrizes.

O produto de dois $N \times N$ matrizes não singulares também é um $N \times N$ matriz não singular que contém propriedade de fechamento.

A multiplicação da matriz em si é associativa. Conseqüentemente, a propriedade associativa é mantida.

O conjunto de $N \times N$ matrizes não singulares contém a matriz de identidade que contém a propriedade do elemento de identidade.

Como todas as matrizes são não singulares, todas têm elementos inversos que também são matrizes não singulares. Conseqüentemente, a propriedade inversa também é válida.

Grupo Abeliano

Um grupo abeliano G é um grupo para o qual o par de elementos $(a,b) \in G$sempre possui lei comutativa. Portanto, um grupo possui cinco propriedades simultaneamente - i) Fechamento, ii) Associativo, iii) Elemento de identidade, iv) Elemento inverso, v) Comutativo.

Exemplo

O conjunto de inteiros positivos (incluindo zero) com operação de adição é um grupo abeliano. $G = \lbrace 0, 1, 2, 3, \dots \rbrace$

Aqui, a propriedade de fechamento é válida para cada par $(a, b) \in S, (a + b)$ está presente no conjunto S. [Por exemplo, $1 + 2 = 2 \in S$ e assim por diante]

A propriedade associativa também é válida para todos os elementos $a, b, c \in S, (a + b) + c = a + (b + c)$ [Por exemplo, $(1 +2) + 3 = 1 + (2 + 3) = 6$ e assim por diante]

A propriedade de identidade também é válida para todos os elementos $a \in S, (a \times e) = a$ [Por exemplo, $(2 \times 1) = 2, (3 \times 1) = 3$e assim por diante]. Aqui, o elemento de identidade é 1.

A propriedade comutativa também é válida para todos os elementos $a \in S, (a \times b) = (b \times a)$ [Por exemplo, $(2 \times 3) = (3 \times 2) = 3$ e assim por diante]

Grupo cíclico e subgrupo

UMA cyclic groupé um grupo que pode ser gerado por um único elemento. Cada elemento de um grupo cíclico é uma potência de algum elemento específico que é chamado de gerador. Um grupo cíclico pode ser gerado por um gerador 'g', de modo que todos os outros elementos do grupo podem ser escritos como uma potência do gerador 'g'.

Exemplo

O conjunto de números complexos $\lbrace 1,-1, i, -i \rbrace$ sob operação de multiplicação é um grupo cíclico.

Existem dois geradores - $i$ e $–i$ Como $i^1 = i, i^2 = -1, i^3 = -i, i^4 = 1$ e também $(–i)^1 = -i, (–i)^2 = -1, (–i)^3 = i, (–i)^4 = 1$que cobre todos os elementos do grupo. Portanto, é um grupo cíclico.

Note - A cyclic groupé sempre um grupo abeliano, mas nem todo grupo abeliano é um grupo cíclico. Os números racionais sob adição não são cíclicos, mas abelianos.

UMA subgroup H é um subconjunto de um grupo G (denotado por $H ≤ G$) se satisfizer as quatro propriedades simultaneamente - Closure, Associative, Identity element, e Inverse.

Um subgrupo H de um grupo G que não inclui todo o grupo G é chamado um subgrupo adequado (indicado por $H < G$) Um subgrupo de um grupo cíclico é cíclico e um subgrupo abeliano também é abeliano.

Exemplo

Deixe um grupo $G = \lbrace 1, i, -1, -i \rbrace$

Então, alguns subgrupos são $H_1 = \lbrace 1 \rbrace, H_2 = \lbrace 1,-1 \rbrace$,

Este não é um subgrupo - $H_3 = \lbrace 1, i \rbrace$ porque aquilo $(i)^{-1} = -i$ não está em $H_3$

Conjunto parcialmente ordenado (POSET)

Um conjunto parcialmente ordenado consiste em um conjunto com uma relação binária que é reflexiva, antissimétrica e transitiva. "Conjunto parcialmente ordenado" é abreviado como POSET.

Exemplos

• O conjunto de números reais sob operação binária menor ou igual a $(\le)$ é um poset.

  Deixe o jogo $S = \lbrace 1, 2, 3 \rbrace$ e a operação é $\le$

  As relações serão $\lbrace(1, 1), (2, 2), (3, 3), (1, 2), (1, 3), (2, 3)\rbrace$

  Esta relação R é reflexiva como $\lbrace (1, 1), (2, 2), (3, 3)\rbrace \in R$

  Esta relação R é anti-simétrica, pois

  $\lbrace (1, 2), (1, 3), (2, 3) \rbrace \in R\ and\ \lbrace (1, 2), (1, 3), (2, 3) \rbrace ∉ R$

  Esta relação R também é transitiva como $\lbrace (1,2), (2,3), (1,3)\rbrace \in R$.

  Portanto, é um poset.

• O conjunto de vértices de um grafo acíclico direcionado sob a operação 'alcançabilidade' é um poset.

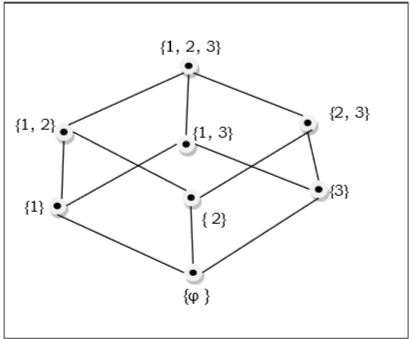
Diagrama de Hasse

O diagrama de Hasse de um poset é o gráfico direcionado cujos vértices são o elemento desse poset e os arcos cobrem os pares (x, y) no poset. Se no poset$x < y$, então o ponto x aparece abaixo do ponto y no diagrama de Hasse. E se$x<y<z$ no poset, a seta não é mostrada entre x e z, pois está implícita.

Exemplo

O poset de subconjuntos de $\lbrace 1, 2, 3 \rbrace = \lbrace \emptyset, \lbrace 1 \rbrace, \lbrace 2 \rbrace, \lbrace 3 \rbrace, \lbrace 1, 2 \rbrace, \lbrace 1, 3 \rbrace, \lbrace 2, 3 \rbrace, \lbrace 1, 2, 3 \rbrace \rbrace$ é mostrado pelo seguinte diagrama de Hasse -

Conjunto ordenado linearmente

Um conjunto ordenado linearmente ou um conjunto ordenado total é um conjunto de ordem parcial em que cada par de elementos é comparável. Os elementos$a, b \in S$ são considerados comparáveis ​​se $a \le b$ ou $b \le a$detém. A lei da tricotomia define esse conjunto ordenado total. Um conjunto totalmente ordenado pode ser definido como uma rede distributiva com a propriedade$\lbrace a \lor b, a \land b \rbrace = \lbrace a, b \rbrace$ para todos os valores de a e b no conjunto S.

Exemplo

O conjunto de poderes de $\lbrace a, b \rbrace$ ordenado por \ subseteq é um conjunto totalmente ordenado como todos os elementos do conjunto de potência $P = \lbrace \emptyset, \lbrace a \rbrace, \lbrace b \rbrace, \lbrace a, b\rbrace \rbrace$ são comparáveis.

Exemplo de conjunto de pedido não total

Um conjunto $S = \lbrace 1, 2, 3, 4, 5, 6 \rbrace$ na operação x divide y não é um conjunto ordenado total.

Aqui para todos $(x, y) \in S, x | y$tem que segurar, mas não é verdade que 2 | 3, como 2 não divide 3 ou 3 não divide 2. Portanto, não é um conjunto ordenado total.

Malha

Uma treliça é um poset $(L, \le)$ para o qual cada par $\lbrace a, b \rbrace \in L$ tem um limite superior mínimo (denotado por $a \lor b$) e um maior limite inferior (denotado por $a \land b$) LUB$(\lbrace a,b \rbrace)$é chamada de junção de a e b. GLB$(\lbrace a,b \rbrace )$ é chamado de encontro de a e b.

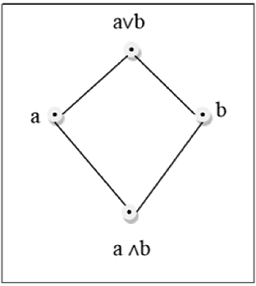
Exemplo

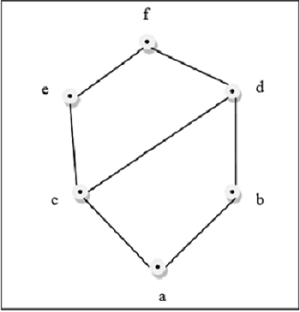
Esta figura acima é uma treliça porque para cada par $\lbrace a, b \rbrace \in L$, existe um GLB e um LUB.

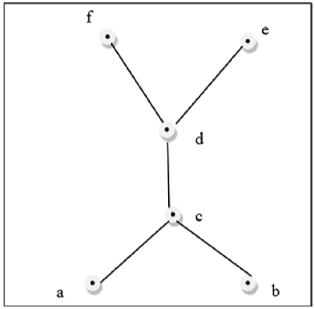
Esta figura acima não é uma treliça porque $GLB (a, b)$ e $LUB (e, f)$ não existe.

Algumas outras redes são discutidas abaixo -

Malha limitada

Uma rede L torna-se uma rede limitada se tiver um maior elemento 1 e um menor elemento 0.

Malha Complementada

Um reticulado L se torna um reticulado complementado se for um reticulado limitado e se cada elemento do reticulado tiver um complemento. Um elemento x tem um complemento x 'se$\exists x(x \land x’=0 and x \lor x’ = 1)$

Malha distributiva

Se uma rede satisfaz as duas propriedades de distribuição a seguir, ela é chamada de rede distributiva.

• $a \lor (b \land c) = (a \lor b) \land (a \lor c)$

• $a \land (b \lor c) = (a \land b) \lor (a \land c)$

Malha Modular

Se uma rede satisfaz a seguinte propriedade, ela é chamada de rede modular.

$a \land( b \lor (a \land d)) = (a \land b) \lor (a \land d)$

Propriedades de reticulados

Propriedades Idempotentes

• $a \lor a = a$

• $a \land a = a$

Propriedades de Absorção

• $a \lor (a \land b) = a$

• $a \land (a \lor b) = a$

Propriedades Comutativas

• $a \lor b = b \lor a$

• $a \land b = b \land a$

Propriedades Associativas

• $a \lor (b \lor c) = (a \lor b) \lor c$

• $a \land (b \land c) = (a \land b) \land c$

Dual of a Lattice

O dual de uma rede é obtido trocando o '$\lor$'e'$\land$' operações.

Exemplo

O dual de $\lbrack a \lor (b \land c) \rbrack\ is\ \lbrack a \land (b \lor c) \rbrack$

Na vida diária, muitas vezes é preciso descobrir o número de todos os resultados possíveis para uma série de eventos. Por exemplo, de quantas maneiras um painel de juízes composto por 6 homens e 4 mulheres pode ser escolhido entre 50 homens e 38 mulheres? Quantos números PAN com 10 letras diferentes podem ser gerados, de modo que as primeiras cinco letras sejam letras maiúsculas, as próximas quatro sejam dígitos e a última seja novamente uma letra maiúscula. Para resolver esses problemas, a teoria matemática da contagem é usada.Counting abrange principalmente a regra de contagem fundamental, a regra de permutação e a regra de combinação.

As regras de soma e produto

o Rule of Sum e Rule of Product são usados ​​para decompor problemas de contagem difíceis em problemas simples.

• The Rule of Sum - Se uma sequência de tarefas $T_1, T_2, \dots, T_m$ pode ser feito em $w_1, w_2, \dots w_m$ maneiras respectivamente (a condição é que nenhuma tarefa possa ser realizada simultaneamente), então o número de maneiras de fazer uma dessas tarefas é $w_1 + w_2 + \dots +w_m$. Se considerarmos duas tarefas A e B que são disjuntas (ou seja$A \cap B = \emptyset$), então matematicamente $|A \cup B| = |A| + |B|$

• The Rule of Product - Se uma sequência de tarefas $T_1, T_2, \dots, T_m$ pode ser feito em $w_1, w_2, \dots w_m$ maneiras, respectivamente, e cada tarefa chega após a ocorrência da tarefa anterior, então há $w_1 \times w_2 \times \dots \times w_m$maneiras de realizar as tarefas. Matematicamente, se uma tarefa B chegar depois de uma tarefa A, então$|A \times B| = |A|\times|B|$

Exemplo

Question- Um menino mora em X e quer ir para a escola em Z. De sua casa X ele tem que primeiro chegar a Y e depois de Y a Z. Ele pode ir de X a Y por 3 rotas de ônibus ou 2 rotas de trem. A partir daí, ele pode escolher 4 rotas de ônibus ou 5 rotas de trem para chegar a Z. Quantas maneiras existem para ir de X a Z?

Solution - De X para Y, ele pode entrar $3 + 2 = 5$formas (Regra da Soma). Depois disso, ele pode ir de Y a Z em$4 + 5 = 9$formas (Regra da Soma). Portanto, de X a Z, ele pode entrar$5 \times 9 = 45$ formas (regra de produto).

Permutações

UMA permutationé um arranjo de alguns elementos em que a ordem é importante. Em outras palavras, uma Permutação é uma combinação ordenada de elementos.

Exemplos

• De um conjunto S = {x, y, z} tomando dois de cada vez, todas as permutações são -

  $ xy, yx, xz, zx, yz, zy $.

• Temos que formar uma permutação de números de três dígitos a partir de um conjunto de números $S = \lbrace 1, 2, 3 \rbrace$. Diferentes números de três dígitos serão formados quando organizarmos os dígitos. A permutação será = 123, 132, 213, 231, 312, 321

Número de Permutações

O número de permutações de 'n' coisas diferentes tomadas 'r' de uma vez é denotado por $n_{P_{r}}$

$$n_{P_{r}} = \frac{n!}{(n - r)!}$$

Onde $n! = 1.2.3. \dots (n - 1).n$

Proof - Que haja 'n' elementos diferentes.

Existem várias maneiras de preencher o primeiro lugar. Depois de preencher o primeiro lugar (n-1), resta o número de elementos. Portanto, existem (n-1) maneiras de preencher a segunda posição. Depois de preencher o primeiro e o segundo lugar, resta (n-2) o número de elementos. Portanto, existem (n-2) maneiras de preencher a terceira posição. Agora podemos generalizar o número de maneiras de preencher a r-ésima casa como [n - (r – 1)] = n – r + 1

Portanto, o total não. de maneiras de preencher do primeiro ao résimo lugar -

$n_{ P_{ r } } = n (n-1) (n-2)..... (n-r + 1)$

$= [n(n-1)(n-2) ... (n-r + 1)] [(n-r)(n-r-1) \dots 3.2.1] / [(n-r)(n-r-1) \dots 3.2.1]$

Conseqüentemente,

$n_{ P_{ r } } = n! / (n-r)!$

Algumas fórmulas importantes de permutação

• Se houver n elementos dos quais$a_1$ são parecidos de algum tipo, $a_2$ são semelhantes de outro tipo; $a_3$ são semelhantes de terceiro tipo e assim por diante e $a_r$ são de $r^{th}$ tipo onde $(a_1 + a_2 + ... a_r) = n$.

  Então, o número de permutações desses n objetos é = $n! / [(a_1!(a_2!) \dots (a_r!)]$.

• Número de permutações de n elementos distintos levando n elementos por vez = $n_{P_n} = n!$

• O número de permutações de n elementos diferentes tomando r elementos por vez, quando x coisas particulares sempre ocupam lugares definidos = $n-x_{p_{r-x}}$

• O número de permutações de n elementos diferentes quando r coisas especificadas sempre vêm juntas é - $r! (n−r+1)!$

• O número de permutações de n elementos diferentes quando r coisas especificadas nunca vêm juntas é - $n!–[r! (n−r+1)!]$

• O número de permutações circulares de n elementos diferentes tomados x elementos no tempo = $^np_{x}/x$

• O número de permutações circulares de n coisas diferentes = $^np_{n}/n$

Alguns problemas

Problem 1 - De um monte de 6 cartas diferentes, de quantas maneiras podemos permutá-lo?

Solution - Como estamos pegando 6 cartas por vez de um baralho de 6 cartas, a permutação será $^6P_{6} = 6! = 720$

Problem 2 - De quantas maneiras as letras da palavra 'READER' podem ser arranjadas?

Solution - Existem 6 letras (2 E, 1 A, 1D e 2R.) Na palavra 'READER'.

A permutação será $= 6! /\: [(2!) (1!)(1!)(2!)] = 180.$

Problem 3 - De que forma as letras da palavra 'LARANJA' podem ser arranjadas de forma que as consoantes ocupem apenas as posições pares?

Solution- Existem 3 vogais e 3 consoantes na palavra 'LARANJA'. Número de maneiras de organizar as consoantes entre si$= ^3P_{3} = 3! = 6$. As 3 vagas restantes serão preenchidas por 3 vogais em$^3P_{3} = 3! = 6$maneiras. Portanto, o número total de permutação é$6 \times 6 = 36$

Combinações

UMA combination é a seleção de alguns elementos dados em que a ordem não importa.

O número de todas as combinações de n coisas, tomadas r de uma vez é -

$$^nC_{ { r } } = \frac { n! } { r!(n-r)! }$$

Problem 1

Encontre o número de subconjuntos do conjunto $\lbrace1, 2, 3, 4, 5, 6\rbrace$ tendo 3 elementos.

Solution

A cardinalidade do conjunto é 6 e temos que escolher 3 elementos do conjunto. Aqui, a ordem não importa. Portanto, o número de subconjuntos será$^6C_{3} = 20$.

Problem 2

Há 6 homens e 5 mulheres em um quarto. De quantas maneiras podemos escolher 3 homens e 2 mulheres na sala?

Solution

O número de maneiras de escolher 3 homens entre 6 homens é $^6C_{3}$ e o número de maneiras de escolher 2 mulheres entre 5 mulheres é $^5C_{2}$

Portanto, o número total de maneiras é - $^6C_{3} \times ^5C_{2} = 20 \times 10 = 200$

Problem 3

De quantas maneiras você pode escolher 3 grupos distintos de 3 alunos de um total de 9 alunos?

Solution

Vamos numerar os grupos como 1, 2 e 3

Para escolher 3 alunos para o ^1º grupo, o número de maneiras -$^9C_{3}$

O número de maneiras de escolher 3 alunos para o ^2º grupo após a escolha do 1º grupo -$^6C_{3}$

O número de maneiras de escolher 3 alunos para o ^3º grupo após a escolha do ^1º e ^2º grupos -$^3C_{3}$

Portanto, o número total de maneiras $= ^9C_{3} \times ^6C_{3} \times ^3C_{3} = 84 \times 20 \times 1 = 1680$

Identidade de Pascal

Identidade de Pascal, primeira derivada por Blaise Pascal em 17 ^th século, estados que o número de maneiras de escolher k elementos de n elementos é igual à soma do número de maneiras de escolher elementos (k-1) a partir de (n-1) elementos e o número de maneiras de escolher elementos de n-1 elementos.

Matematicamente, para quaisquer inteiros positivos k e n: $^nC_{k} = ^n{^-}^1C_{k-1} + ^n{^-}^1{C_k}$

Proof -

$$^n{^-}^1C_{k-1} + ^n{^-}^1{C_k}$$

$= \frac{ (n-1)! } { (k-1)!(n-k)! } + \frac{ (n-1)! } { k!(n-k-1)! }$

$= (n-1)!(\frac{ k } { k!(n-k)! } + \frac{ n-k } { k!(n-k)! } )$

$= (n-1)! \frac{ n } { k!(n-k)! }$

$= \frac{ n! } { k!(n-k)! }$

$= n_{ C_{ k } }$

Princípio do buraco do pombo

Em 1834, o matemático alemão Peter Gustav Lejeune Dirichlet estabeleceu um princípio que chamou de princípio da gaveta. Agora, é conhecido como o princípio do escaninho.

Pigeonhole Principleafirma que, se houver menos pombos do que o número total de pombos e cada pombo for colocado em uma pomba, então deve haver pelo menos um pombo com mais de um pombo. Se n pombos forem colocados em m escaninhos, onde n> m, haverá um buraco com mais de um pombo.

Exemplos

• Dez homens estão em uma sala e participam de apertos de mão. Se cada pessoa aperta a mão pelo menos uma vez e nenhum homem aperta a mão do mesmo homem mais de uma vez, então dois homens participam do mesmo número de apertos de mão.

• Deve haver pelo menos duas pessoas em uma classe de 30 alunos cujos nomes comecem com o mesmo alfabeto.

O princípio de inclusão-exclusão

o Inclusion-exclusion principlecalcula o número cardinal da união de vários conjuntos não disjuntos. Para dois conjuntos A e B, o princípio afirma -

$|A \cup B| = |A| + |B| - |A \cap B|$

Para três conjuntos A, B e C, o princípio afirma -

$|A \cup B \cup C | = |A| + |B| + |C| - |A \cap B| - |A \cap C| - |B \cap C| + |A \cap B \cap C |$

A fórmula generalizada -

$|\bigcup_{i=1}^{n}A_i|=\sum\limits_{1\leq i<j<k\leq n}|A_i \cap A_j|+\sum\limits_{1\leq i<j<k\leq n}|A_i \cap A_j \cap A_k|- \dots +(-1)^{\pi-1}|A_1 \cap \dots \cap A_2|$

Problem 1

Quantos inteiros de 1 a 50 são múltiplos de 2 ou 3, mas não ambos?

Solution

De 1 a 100, existem $50/2 = 25$ números que são múltiplos de 2.

tem $50/3 = 16$ números que são múltiplos de 3.

tem $50/6 = 8$ números que são múltiplos de 2 e 3.

Então, $|A|=25$, $|B|=16$ e $|A \cap B|= 8$.

$|A \cup B| = |A| + |B| - |A \cap B| = 25 + 16 - 8 = 33$

Problem 2

Em um grupo de 50 alunos, 24 gostam de bebidas geladas e 36 gostam de bebidas quentes e cada aluno gosta de pelo menos uma das duas bebidas. Quantos gostam de café e chá?

Solution

Seja X o conjunto de alunos que gostam de bebidas frias e Y o conjunto de pessoas que gostam de bebidas quentes.

Então, $| X \cup Y | = 50$, $|X| = 24$, $|Y| = 36$

$|X \cap Y| = |X| + |Y| - |X \cup Y| = 24 + 36 - 50 = 60 - 50 = 10$

Portanto, há 10 alunos que gostam tanto de chá quanto de café.

Intimamente relacionado aos conceitos de contagem está a Probabilidade. Freqüentemente, tentamos adivinhar os resultados de jogos de azar, como jogos de cartas, caça-níqueis e loterias; ou seja, tentamos encontrar a probabilidade de que um determinado resultado seja obtido.

Probabilitypode ser conceituado como encontrar a chance de ocorrência de um evento. Matematicamente, é o estudo de processos aleatórios e seus resultados. As leis da probabilidade têm ampla aplicabilidade em uma variedade de campos, como genética, previsão do tempo, pesquisas de opinião, mercado de ações, etc.

Conceitos Básicos

A teoria da probabilidade foi inventada no século 17 por dois matemáticos franceses, Blaise Pascal e Pierre de Fermat, que lidavam com problemas matemáticos relacionados ao acaso.

Antes de prosseguir com os detalhes da probabilidade, vamos obter o conceito de algumas definições.

Random Experiment- Um experimento no qual todos os resultados possíveis são conhecidos e a saída exata não pode ser prevista com antecedência é chamado de experimento aleatório. Jogar uma moeda justa é um exemplo de experimento aleatório.

Sample Space- Quando realizamos um experimento, o conjunto S de todos os resultados possíveis é chamado de espaço amostral. Se jogarmos uma moeda, o espaço de amostra$S = \left \{ H, T \right \}$

Event- Qualquer subconjunto de um espaço de amostra é chamado de evento. Depois de jogar uma moeda, colocar a Cabeça no topo é um evento.

A palavra "probabilidade" significa a chance de ocorrência de um evento específico. O melhor que podemos dizer é qual a probabilidade de acontecer, usando a ideia de probabilidade.

$Probability\:of\:occurence\:of\:an\:event = \frac{Total\:number\:of\:favourable \: outcome}{Total\:number\:of\:Outcomes}$

Como a ocorrência de algum evento varia entre 0% e 100%, a probabilidade varia entre 0 e 1.

Passos para encontrar a probabilidade

Etapa 1 - Calcule todos os resultados possíveis do experimento.

Etapa 2 - Calcule o número de resultados favoráveis ​​do experimento.

Etapa 3 - Aplicar a fórmula de probabilidade correspondente.

Jogando uma moeda

Se uma moeda for lançada, existem dois resultados possíveis - Cara $(H)$ ou caudas $(T)$

Portanto, número total de resultados = 2

Portanto, a probabilidade de obter uma Cabeça $(H)$ no topo é 1/2 e a probabilidade de obter uma cauda $(T)$ no topo é 1/2

Jogando um Dado

Quando um dado é lançado, seis resultados possíveis podem estar no topo - $1, 2, 3, 4, 5, 6$.

A probabilidade de qualquer um dos números é 1/6

A probabilidade de obter números pares é 3/6 = 1/2

A probabilidade de obter números ímpares é 3/6 = 1/2

Pegando cartas de um baralho

Em um baralho de 52 cartas, se uma carta for escolhida, calcule a probabilidade de um ás ser sorteado e também a probabilidade de um ouros ser sorteado.

Número total de resultados possíveis - 52

Resultado de ser um ás - 4

Probabilidade de ser um ás = 4/52 = 1/13

Probabilidade de ser um diamante = 13/52 = 1/4

Axiomas de probabilidade

• A probabilidade de um evento sempre varia de 0 a 1. $[0 \leq P(x) \leq 1]$

• Para um evento impossível, a probabilidade é 0 e para um certo evento a probabilidade é 1.

• Se a ocorrência de um evento não é influenciada por outro evento, eles são chamados de mutuamente exclusivos ou separados.

  E se $A_1, A_2....A_n$ são eventos mutuamente exclusivos / disjuntos, então $P(A_i \cap A_j) = \emptyset $ para $i \ne j$ e $P(A_1 \cup A_2 \cup.... A_n) = P(A_1) + P(A_2)+..... P(A_n)$

Propriedades de probabilidade

• Se houver dois eventos $x$ e $\overline{x}$que são complementares, então a probabilidade do evento complementar é -

  $$p(\overline{x}) = 1-p(x)$$

• Para dois eventos não disjuntos A e B, a probabilidade de união de dois eventos -

  $P(A \cup B) = P(A) + P(B)$

• Se um evento A é um subconjunto de outro evento B (ou seja, $A \subset B$), então a probabilidade de A é menor ou igual à probabilidade de B. Portanto, $A \subset B$ implica $P(A) \leq p(B)$

Probabilidade Condicional

A probabilidade condicional de um evento B é a probabilidade de que o evento ocorra, dado que um evento A já ocorreu. Isto é escrito como$P(B|A)$.

Matematicamente - $ P(B|A) = P(A \cap B)/ P(A)$

Se o evento A e B são mutuamente exclusivos, então a probabilidade condicional do evento B após o evento A será a probabilidade do evento B que é $P(B)$.

Problem 1

Em um país, 50% de todos os adolescentes possuem uma bicicleta e 30% de todos os adolescentes possuem uma bicicleta e bicicleta. Qual é a probabilidade de um adolescente possuir bicicleta, visto que o adolescente possui uma bicicleta?

Solution

Suponhamos que A seja o evento de adolescentes que possuem apenas uma bicicleta e B é o evento de adolescentes que possuem apenas uma bicicleta.

Então, $P(A) = 50/100 = 0.5$ e $P(A \cap B) = 30/100 = 0.3$ do problema fornecido.

$P(B|A) = P(A \cap B)/ P(A) = 0.3/ 0.5 = 0.6$

Assim, a probabilidade de um adolescente possuir bicicleta, visto que o adolescente possui uma bicicleta, é de 60%.

Problem 2

Em uma classe, 50% de todos os alunos jogam críquete e 25% de todos os alunos jogam críquete e vôlei. Qual é a probabilidade de um aluno jogar vôlei, visto que o aluno joga críquete?

Solution

Suponhamos que A é o evento de alunos que jogam apenas críquete e B é o evento de alunos que jogam apenas voleibol.

Então, $P(A) = 50/100 =0.5$ e $P(A \cap B) = 25/ 100 =0.25$ do problema fornecido.

$P\lgroup B\rvert A \rgroup= P\lgroup A\cap B\rgroup/P\lgroup A \rgroup =0.25/0.5=0.5$

Portanto, a probabilidade de um aluno jogar voleibol dado que o aluno joga críquete é de 50%.

Problem 3

Seis laptops bons e três laptops defeituosos estão misturados. Para encontrar os laptops com defeito, todos eles são testados um a um aleatoriamente. Qual é a probabilidade de encontrar os dois laptops com defeito nas duas primeiras opções?

Solution

Seja A o evento em que encontramos um laptop com defeito no primeiro teste e B o evento em que encontramos um laptop com defeito no segundo teste.

Conseqüentemente, $P(A \cap B) = P(A)P(B|A) =3/9 \times 2/8 = 1/12$

Teorema de Bayes

Theorem - Se A e B forem dois eventos mutuamente exclusivos, onde $P(A)$ é a probabilidade de A e $P(B)$ é a probabilidade de B, $P(A | B)$ é a probabilidade de A, dado que B é verdadeiro. $P(B | A)$ é a probabilidade de B dado que A é verdadeiro, então o teorema de Bayes afirma -

$$P(A|B) = \frac{P(B|A) P(A)}{\sum_{i = 1}^{n}P(B|Ai)P(Ai)}$$

Aplicação do Teorema de Bayes

• Em situações em que todos os eventos do espaço de amostra são eventos mutuamente exclusivos.

• Em situações em que $P( A_i \cap B )$ para cada $A_i$ ou $P( A_i )$ e $P(B|A_i)$ para cada $A_i$ é conhecido.

Problem

Considere três suportes para canetas. O primeiro suporte para canetas contém 2 canetas vermelhas e 3 canetas azuis; o segundo possui 3 canetas vermelhas e 2 canetas azuis; e o terceiro possui 4 canetas vermelhas e 1 caneta azul. A probabilidade de cada suporte de caneta ser selecionado é igual. Se uma caneta for desenhada ao acaso, qual é a probabilidade de que seja uma caneta vermelha?

Solution

Deixei $A_i$ser o evento que i ^th pen-stand é selecionado.

Aqui, i = 1,2,3.

Uma vez que a probabilidade de escolher um suporte para caneta é igual, $P(A_i) = 1/3$

Seja B o evento em que uma caneta vermelha é desenhada.

A probabilidade de que uma caneta vermelha seja escolhida entre as cinco canetas do primeiro suporte para canetas,

$P(B|A_1) = 2/5$

A probabilidade de que uma caneta vermelha seja escolhida entre as cinco canetas do segundo suporte para canetas,

$P(B|A_2) = 3/5$

A probabilidade de que uma caneta vermelha seja escolhida entre as cinco canetas do terceiro suporte para canetas,

$P(B|A_3) = 4/5$

De acordo com o Teorema de Bayes,

$P(B) = P(A_1).P(B|A_1) + P(A_2).P(B|A_2) + P(A_3).P(B|A_3)$

$= 1/3 . 2/5\: +\: 1/3 . 3/5\: +\: 1/3 . 4/5$

$= 3/5$

Mathematical induction, é uma técnica para provar resultados ou estabelecer afirmações para números naturais. Esta parte ilustra o método por meio de uma variedade de exemplos.

Definição

Mathematical Induction é uma técnica matemática que é usada para provar uma afirmação, uma fórmula ou um teorema verdadeiro para todos os números naturais.

A técnica envolve duas etapas para provar uma afirmação, conforme declarado abaixo -

Step 1(Base step) - Prova que uma afirmação é verdadeira para o valor inicial.

Step 2(Inductive step)- Prova que se a afirmação é verdadeira para a ^enésima iteração (ou número n ), então também é verdadeira para (n + 1) ^a iteração (ou número n + 1 ).

Como fazer isso

Step 1- Considere um valor inicial para o qual a afirmação é verdadeira. Deve ser mostrado que a afirmação é verdadeira para n = valor inicial.

Step 2- Suponha que a afirmação seja verdadeira para qualquer valor de n = k . Em seguida, prove que a afirmação é verdadeira para n = k + 1 . Na verdade, dividimos n = k + 1 em duas partes, uma parte é n = k (o que já está provado) e tentamos provar a outra parte.

Problema 1

$3^n-1$ é um múltiplo de 2 para n = 1, 2, ...

Solution

Step 1 - para $n = 1, 3^1-1 = 3-1 = 2$ que é um múltiplo de 2

Step 2 - Vamos supor $3^n-1$ é verdade para $n=k$, Conseqüentemente, $3^k -1$ é verdade (é uma suposição)

Temos que provar isso $3^{k+1}-1$ também é um múltiplo de 2

$3^{k+1} - 1 = 3 \times 3^k - 1 = (2 \times 3^k) + (3^k - 1)$

A primeira parte $(2 \times 3k)$ é certo que será um múltiplo de 2 e a segunda parte $(3k -1)$ também é verdade como nossa suposição anterior.

Conseqüentemente, $3^{k+1} – 1$ é um múltiplo de 2.

Então, está provado que $3^n – 1$ é um múltiplo de 2.

Problema 2

$1 + 3 + 5 + ... + (2n-1) = n^2$ para $n = 1, 2, \dots $

Solution

Step 1 - para $n=1, 1 = 1^2$, Portanto, a etapa 1 é satisfeita.

Step 2 - Suponhamos que a afirmação seja verdadeira para $n=k$.

Conseqüentemente, $1 + 3 + 5 + \dots + (2k-1) = k^2$ é verdade (é uma suposição)

Temos que provar isso $1 + 3 + 5 + ... + (2(k+1)-1) = (k+1)^2$ também detém

$1 + 3 + 5 + \dots + (2(k+1) - 1)$

$= 1 + 3 + 5 + \dots + (2k+2 - 1)$

$= 1 + 3 + 5 + \dots + (2k + 1)$

$= 1 + 3 + 5 + \dots + (2k - 1) + (2k + 1)$

$= k^2 + (2k + 1)$

$= (k + 1)^2$

Então, $1 + 3 + 5 + \dots + (2(k+1) - 1) = (k+1)^2$ segure que satisfaça a etapa 2.

Conseqüentemente, $1 + 3 + 5 + \dots + (2n - 1) = n^2$ está provado.

Problema 3

Provar que $(ab)^n = a^nb^n$ é verdade para todo número natural $n$

Solution

Step 1 - para $n=1, (ab)^1 = a^1b^1 = ab$, Portanto, a etapa 1 é satisfeita.

Step 2 - Suponhamos que a afirmação seja verdadeira para $n=k$, Conseqüentemente, $(ab)^k = a^kb^k$ é verdade (é uma suposição).

Temos que provar isso $(ab)^{k+1} = a^{k+1}b^{k+1}$ também segurar

Dado, $(ab)^k = a^k b^k$

Ou, $(ab)^k (ab) = (a^k b^k ) (ab)$ [Multiplicando ambos os lados por 'ab']

Ou, $(ab)^{k+1} = (aa^k) ( bb^k)$

Ou, $(ab)^{k+1} = (a^{k+1}b^{k+1})$

Portanto, a etapa 2 está comprovada.

Então, $(ab)^n = a^nb^n$ é verdadeiro para todo número natural n.

Indução forte

A indução forte é outra forma de indução matemática. Através desta técnica de indução, podemos provar que uma função proposicional,$P(n)$ é verdadeiro para todos os inteiros positivos, $n$, usando as seguintes etapas -

• Step 1(Base step) - Isso prova que a proposição inicial $P(1)$ verdadeiro.

• Step 2(Inductive step) - Isso prova que a declaração condicional $[P(1) \land P(2) \land P(3) \land \dots \land P(k)] → P(k + 1)$ é verdadeiro para inteiros positivos $k$.

Neste capítulo, discutiremos como as técnicas recursivas podem derivar sequências e ser usadas para resolver problemas de contagem. O procedimento para encontrar os termos de uma sequência de maneira recursiva é chamadorecurrence relation. Estudamos a teoria das relações de recorrência linear e suas soluções. Finalmente, introduzimos funções geradoras para resolver relações de recorrência.

Definição

Uma relação de recorrência é uma equação que define recursivamente uma sequência onde o próximo termo é uma função dos termos anteriores (Expressando $F_n$ como alguma combinação de $F_i$ com $i < n$)

Example - Série Fibonacci - $F_n = F_{n-1} + F_{n-2}$, Torre de Hanói - $F_n = 2F_{n-1} + 1$

Relações de recorrência linear

Uma equação de recorrência linear de grau k ou ordem k é uma equação de recorrência que está no formato $x_n= A_1 x_{n-1}+ A_2 x_{n-1}+ A_3 x_{n-1}+ \dots A_k x_{n-k} $($A_n$ é uma constante e $A_k \neq 0$) em uma sequência de números como um polinômio de primeiro grau.

Estes são alguns exemplos de equações de recorrência linear -

Relações de recorrência	Valores iniciais	Soluções
F n = F n-1 + F n-2	a 1 = a 2 = 1	Número de Fibonacci
F n = F n-1 + F n-2	a 1 = 1, a 2 = 3	Número lucas
F n = F n-2 + F n-3	a 1 = a 2 = a 3 = 1	Sequência Padovan
F n = 2F n-1 + F n-2	a 1 = 0, a 2 = 1	Número Pell

Como resolver a relação de recorrência linear

Suponha que uma relação de recorrência linear de duas ordens seja - $F_n = AF_{n-1} +BF_{n-2}$ onde A e B são números reais.

A equação característica para a relação de recorrência acima é -

$$x^2 - Ax - B = 0$$

Três casos podem ocorrer ao encontrar as raízes -

Case 1 - Se esta equação fatora como $(x- x_1)(x- x_1) = 0$ e produz duas raízes reais distintas $x_1$ e $x_2$, então $F_n = ax_1^n+ bx_2^n$é a solução. [Aqui, a e b são constantes]

Case 2 - Se esta equação fatora como $(x- x_1)^2 = 0$ e produz uma única raiz real $x_1$, então $F_n = a x_1^n+ bn x_1^n$ é a solução.

Case 3 - Se a equação produz duas raízes complexas distintas, $x_1$ e $x_2$ na forma polar $x_1 = r \angle \theta$ e $x_2 = r \angle(- \theta)$, então $F_n = r^n (a cos(n\theta)+ b sin(n\theta))$ é a solução.

Problem 1

Resolva a relação de recorrência $F_n = 5F_{n-1} - 6F_{n-2}$ Onde $F_0 = 1$ e $F_1 = 4$

Solution

A equação característica da relação de recorrência é -

$$x^2 - 5x + 6 = 0,$$

Então, $(x - 3) (x - 2) = 0$

Portanto, as raízes são -

$x_1 = 3$ e $x_2 = 2$

As raízes são reais e distintas. Então, isso está na forma do caso 1

Portanto, a solução é -

$$F_n = ax_1^n + bx_2^n$$

Aqui, $F_n = a3^n + b2^n\ (As\ x_1 = 3\ and\ x_2 = 2)$

Portanto,

$1 = F_0 = a3^0 + b2^0 = a+b$

$4 = F_1 = a3^1 + b2^1 = 3a+2b$

Resolvendo essas duas equações, temos $ a = 2$ e $b = -1$

Portanto, a solução final é -

$$F_n = 2.3^n + (-1) . 2^n = 2.3^n - 2^n $$

Problem 2

Resolva a relação de recorrência - $F_n = 10F_{n-1} - 25F_{n-2}$ Onde $F_0 = 3$ e $F_1 = 17$

Solution

A equação característica da relação de recorrência é -

$$ x^2 - 10x -25 = 0$$

então $(x - 5)^2 = 0$

Portanto, há uma única raiz real $x_1 = 5$

Como há uma única raiz de valor real, isso está na forma do caso 2

Portanto, a solução é -

$F_n = ax_1^n + bnx_1^n$

$3 = F_0 = a.5^0 +(b)(0.5)^0 = a$

$17 = F_1 = a.5^1 + b.1.5^1 = 5a+5b$

Resolvendo essas duas equações, temos $a = 3$ e $b = 2/5$

Portanto, a solução final é - $F_n = 3.5^n +( 2/5) .n.2^n $

Problem 3

Resolva a relação de recorrência $F_n = 2F_{n-1} - 2F_{n-2}$ Onde $F_0 = 1$ e $F_1 = 3$

Solution

A equação característica da relação de recorrência é -

$$x^2 -2x -2 = 0$$

Portanto, as raízes são -

$x_1 = 1 + i$ e $x_2 = 1 - i$

Na forma polar,

$x_1 = r \angle \theta$ e $x_2 = r \angle(- \theta),$ Onde $r = \sqrt 2$ e $\theta = \frac{\pi}{4}$

As raízes são imaginárias. Então, isso está na forma do caso 3.

Portanto, a solução é -

$F_n = (\sqrt 2 )^n (a cos(n .\sqcap /4) + b sin(n .\sqcap /4))$

$1 = F_0 = (\sqrt 2 )^0 (a cos(0 .\sqcap /4) + b sin(0 .\sqcap /4) ) = a$

$3 = F_1 = (\sqrt 2 )^1 (a cos(1 .\sqcap /4) + b sin(1 . \sqcap /4) ) = \sqrt 2 ( a/ \sqrt 2 + b/ \sqrt 2)$

Resolvendo essas duas equações, obtemos $a = 1$ e $b = 2$

Portanto, a solução final é -

$F_n = (\sqrt 2 )^n (cos(n .\pi /4 ) + 2 sin(n .\pi /4 ))$

Relação de recorrência não homogênea e soluções particulares

Uma relação de recorrência é chamada de não homogênea se estiver na forma

$F_n = AF_{n-1} + BF_{n-2} + f(n)$ Onde $f(n) \ne 0$

Sua relação de recorrência homogênea associada é $F_n = AF_{n–1} + BF_{n-2}$

A solução $(a_n)$ de uma relação de recorrência não homogênea tem duas partes.

A primeira parte é a solução $(a_h)$ da relação de recorrência homogênea associada e a segunda parte é a solução particular $(a_t)$.

$$a_n=a_h+a_t$$

A solução da primeira parte é feita usando os procedimentos discutidos na seção anterior.

Para encontrar a solução específica, encontramos uma solução de teste apropriada.

Deixei $f(n) = cx^n$; deixei$x^2 = Ax + B$ seja a equação característica da relação de recorrência homogênea associada e deixe $x_1$ e $x_2$ ser suas raízes.

• E se $x \ne x_1$ e $x \ne x_2$, então $a_t = Ax^n$

• E se $x = x_1$, $x \ne x_2$, então $a_t = Anx^n$

• E se $x = x_1 = x_2$, então $a_t = An^2x^n$

Exemplo

Deixe uma relação de recorrência não homogênea ser $F_n = AF_{n–1} + BF_{n-2} + f(n)$ com raízes características $x_1 = 2$ e $x_2 = 5$. Soluções de teste para diferentes valores possíveis de$f(n)$ são os seguintes -