Simplificação de funções booleanas
Simplificação usando funções algébricas
Nesta abordagem, uma expressão booleana é minimizada em uma expressão equivalente aplicando identidades booleanas.
Problema 1
Minimize a seguinte expressão booleana usando identidades booleanas -
$$ F (A, B, C) = A'B + BC '+ BC + AB'C' $$
Solução
Dado, $ F (A, B, C) = A'B + BC '+ BC + AB'C' $
Ou $ F (A, B, C) = A'B + (BC '+ BC') + BC + AB'C '$
[Pela lei idempotente, BC '= BC' + BC ']
Ou $ F (A, B, C) = A'B + (BC '+ BC) + (BC' + AB'C ') $
Ou $ F (A, B, C) = A'B + B (C '+ C) + C' (B + AB ') $
[Por leis distributivas]
Ou $ F (A, B, C) = A'B + B.1 + C '(B + A) $
[(C '+ C) = 1 e lei de absorção (B + AB') = (B + A)]
Ou $ F (A, B, C) = A'B + B + C '(B + A) $
[B.1 = B]
Ou $ F (A, B, C) = B (A '+ 1) + C' (B + A) $
Ou $ F (A, B, C) = B.1 + C '(B + A) $
[(A '+ 1) = 1]
Ou $ F (A, B, C) = B + C '(B + A) $
[As, B.1 = B]
Ou $ F (A, B, C) = B + BC '+ AC' $
Ou $ F (A, B, C) = B (1 + C ') + AC' $
Ou $ F (A, B, C) = B.1 + AC '$
[Como, (1 + C ') = 1]
Ou $ F (A, B, C) = B + AC '$
[As, B.1 = B]
Portanto, $ F (A, B, C) = B + AC '$ é a forma minimizada.
Problema 2
Minimize a seguinte expressão booleana usando identidades booleanas -
$$ F (A, B, C) = (A + B) (A + C) $$
Solução
Dado, $ F (A, B, C) = (A + B) (A + C) $
Ou, $ F (A, B, C) = AA + AC + BA + BC $ [Aplicando regra distributiva]
Ou $ F (A, B, C) = A + AC + BA + BC $ [Aplicando a Lei Idempotente]
Ou $ F (A, B, C) = A (1 + C) + BA + BC $ [Aplicando a lei distributiva]
Ou $ F (A, B, C) = A + BA + BC $ [Aplicando Lei de Dominância]
Ou $ F (A, B, C) = (A + 1) .A + BC $ [Aplicando a Lei distributiva]
Ou $ F (A, B, C) = 1.A + BC $ [Aplicando a Lei de Dominância]
Ou, $ F (A, B, C) = A + BC $ [Aplicando Lei de Dominância]
Portanto, $ F (A, B, C) = A + BC $ é a forma minimizada.
Mapas de Karnaugh
O mapa de Karnaugh (K-map), introduzido por Maurice Karnaughin em 1953, é uma representação em forma de grade de uma tabela verdade que é usada para simplificar as expressões da álgebra booleana. Um mapa de Karnaugh tem zero e uma entrada em posições diferentes. Ele fornece agrupamento de expressões booleanas com fatores comuns e elimina variáveis indesejadas da expressão. Em um K-map, cruzar um limite de célula vertical ou horizontal é sempre uma mudança de apenas uma variável.
Exemplo 1
Uma tabela de verdade arbitrária é obtida abaixo -
| UMA | B | A operação B |
|---|---|---|
| 0 | 0 | W |
| 0 | 1 | x |
| 1 | 0 | y |
| 1 | 1 | z |
Agora faremos um k-map para a tabela verdade acima -

Exemplo 2
Agora faremos um K-map para a expressão - AB + A'B '
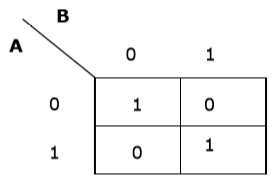
Simplificação usando K-map
O K-map usa algumas regras para a simplificação das expressões booleanas combinando células adjacentes em um único termo. As regras são descritas abaixo -
Rule 1 - Qualquer célula contendo um zero não pode ser agrupada.
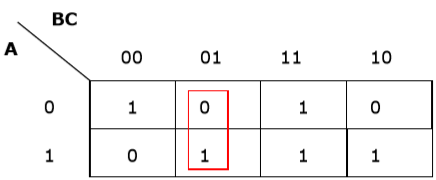
Agrupamento errado
Rule 2 - Os grupos devem conter 2n células (n começando em 1).
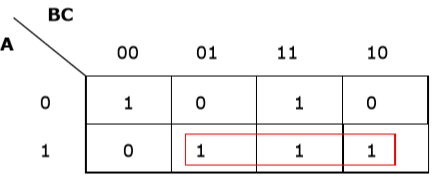
Agrupamento errado
Rule 3 - O agrupamento deve ser horizontal ou vertical, mas não deve ser diagonal.
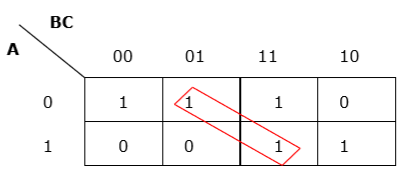
Agrupamento diagonal errado
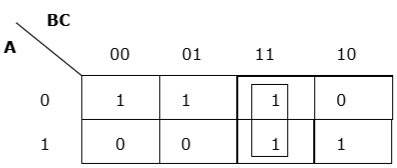
Agrupamento vertical adequado
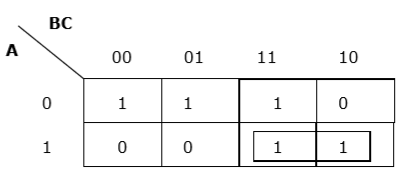
Agrupamento horizontal adequado
Rule 4 - Os grupos devem ser cobertos o máximo possível.
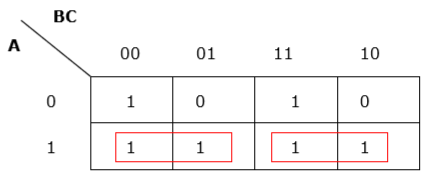
Agrupamento insuficiente
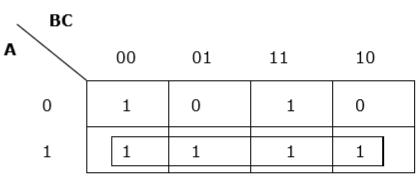
Agrupamento adequado
Rule 5 - Se 1 de qualquer célula não puder ser agrupada com nenhuma outra célula, ela atuará como um grupo.
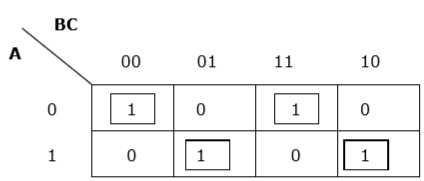
Agrupamento adequado
Rule 6 - Os grupos podem se sobrepor, mas deve haver o menor número possível de grupos.
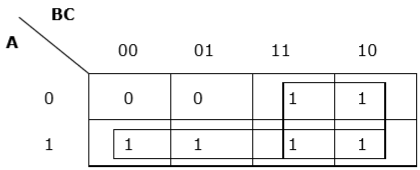
Agrupamento adequado
Rule 7 - As células / células mais à esquerda podem ser agrupadas com as células / células mais à direita e as células / células mais altas podem ser agrupadas com as células / células mais baixas.
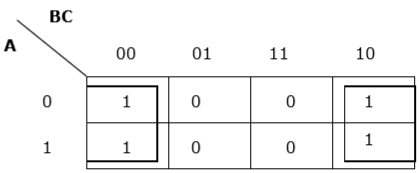
Agrupamento adequado
Problema
Minimize a seguinte expressão booleana usando K-map -
$$ F (A, B, C) = A'BC + A'BC '+ AB'C' + AB'C $$
Solução
Cada termo é colocado no k-map e obtemos o seguinte -
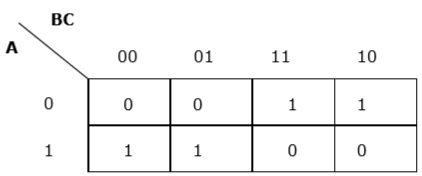
K-map para F (A, B, C)
Agora vamos agrupar as células de 1 de acordo com as regras declaradas acima -
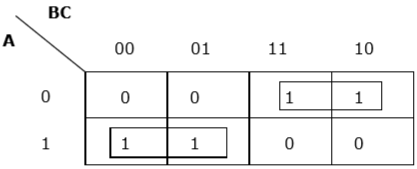
K-map para F (A, B, C)
Temos dois grupos denominados $ A'B $ e $ AB '$. Portanto, $ F (A, B, C) = A'B + AB '= A \ oplus B $. É a forma minimizada.