Matemática Discreta - Mais Sobre Gráficos

Coloração de Gráfico

A coloração do gráfico é o procedimento de atribuição de cores a cada vértice de um gráfico G de forma que nenhum vértice adjacente obtenha a mesma cor. O objetivo é minimizar o número de cores ao colorir um gráfico. O menor número de cores necessário para colorir um gráfico G é chamado de número cromático desse gráfico. O problema de coloração do gráfico é um problema NP Completo.

Método para colorir um gráfico

As etapas necessárias para colorir um gráfico G com n número de vértices são as seguintes -

Step 1 - Organize os vértices do gráfico em alguma ordem.

Step 2 - Escolha o primeiro vértice e pinte-o com a primeira cor.

Step 3- Escolha o próximo vértice e pinte-o com a cor de menor número que não foi colorida em nenhum vértice adjacente a ele. Se todos os vértices adjacentes forem coloridos com esta cor, atribua uma nova cor a ele. Repita esta etapa até que todos os vértices estejam coloridos.

Example

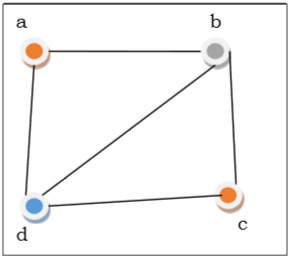
Na figura acima, no primeiro vértice $ a $ é colorido de vermelho. Como os vértices adjacentes do vértice a são novamente adjacentes, o vértice $ b $ e o vértice $ d $ são coloridos com cores diferentes, verde e azul respectivamente. Então, o vértice $ c $ é tão vermelho quanto nenhum vértice adjacente de $ c $ é colorido de vermelho. Portanto, poderíamos colorir o gráfico com 3 cores. Portanto, o número cromático do gráfico é 3.

Aplicações da coloração de grafos

Algumas aplicações de colorir gráficos incluem -

Registrar Alocação
Coloração do mapa
Verificação de gráfico bipartido
Atribuição de radiofrequência móvel
Fazendo cronograma, etc.

Gráfico Traversal

A travessia do gráfico é o problema de visitar todos os vértices de um gráfico em alguma ordem sistemática. Existem basicamente duas maneiras de percorrer um gráfico.

Largura da primeira pesquisa
Profundidade primeira pesquisa

Largura da primeira pesquisa

A primeira pesquisa de amplitude (BFS) começa no vértice de nível 0 $ X $ do gráfico $ G $. Em seguida, visitamos todos os vértices que são vizinhos de $ X $. Após a visita, marcamos os vértices como "visitados" e os colocamos no nível 1. Em seguida, começamos a partir dos vértices de nível 1 e aplicamos o mesmo método em todos os vértices de nível 1 e assim por diante. O percurso BFS termina quando todos os vértices do gráfico são visitados.

BFS Algorithm

O conceito é visitar todos os vértices vizinhos antes de visitar outros vértices vizinhos de vértices vizinhos.

Inicialize o status de todos os nós como “Pronto”.
Coloque o vértice de origem em uma fila e mude seu status para “Esperando”.
Repita as duas etapas a seguir até que a fila esteja vazia -
- Remova o primeiro vértice da fila e marque-o como “Visitado”.
- Adicione à parte traseira da fila todos os vizinhos do vértice removido cujo status é “Pronto”. Marque seu status como “Esperando”.

Problem

Vamos pegar um gráfico (o vértice de origem é 'a') e aplicar o algoritmo BFS para descobrir a ordem de travessia.

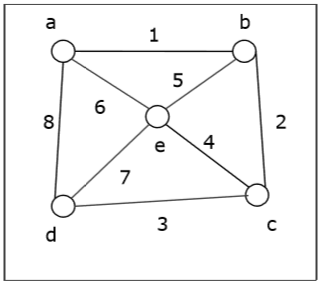
Solution -

Inicialize o status de todos os vértices para “Pronto”.
Coloque um na fila e mude seu status para “Esperando”.
Remova um da fila, marque-o como “Visitado”.
Adicionar um ‘s vizinhos em‘Ready’estado b, d e e até o fim da fila e marcá-los como‘espera’.
Remova b da fila, marque-o como “Visitado”, coloque seu vizinho “Pronto” c no final da fila e marque c como “Esperando”.
Remova d da fila e marque-o como “Visitados”. Não tem vizinho no estado “Pronto”.
Remova e da fila e marque-o como “Visitado”. Não tem vizinho no estado “Pronto”.
Remova c da fila e marque-o como “Visitado”. Não tem vizinho no estado “Pronto”.
A fila está vazia, então pare.

Portanto, a ordem de passagem é -

$ a \ rightarrow b \ rightarrow d \ rightarrow e \ rightarrow c $

As ordens alternativas de travessia são -

$ a \ rightarrow b \ rightarrow e \ rightarrow d \ rightarrow c $

Ou $ a \ rightarrow d \ rightarrow b \ rightarrow e \ rightarrow c $

Ou $ a \ rightarrow e \ rightarrow b \ rightarrow d \ rightarrow c $

Ou $ a \ rightarrow b \ rightarrow e \ rightarrow d \ rightarrow c $

Ou $ a \ rightarrow d \ rightarrow e \ rightarrow b \ rightarrow c $

Application of BFS

Encontrando o caminho mais curto
Árvore de abrangência mínima para gráfico não ponderado
Sistema de navegação GPS
Detectando ciclos em um gráfico não direcionado
Encontrar todos os nós em um componente conectado

Complexity Analysis

Seja $ G (V, E) $ um gráfico com $ | V | $ número de vértices e $ | E | $ número de arestas. Se o algoritmo de pesquisa em amplitude visitar todos os vértices do gráfico e verificar todas as arestas, então sua complexidade de tempo seria -

$$ O (| V | + | E |). O (| E |) $$

Pode variar entre $ O (1) $ e $ O (| V2 |) $

Profundidade primeira pesquisa

O algoritmo Depth First Search (DFS) começa a partir de um vértice $ v $, então atravessa seu vértice adjacente (digamos x) que não foi visitado antes e marca como "visitado" e continua com o vértice adjacente de $ x $ e em breve.

Se em qualquer vértice, ele encontra que todos os vértices adjacentes foram visitados, então ele retrocede até encontrar o primeiro vértice tendo um vértice adjacente que não foi percorrido antes. Então, ele atravessa aquele vértice, continua com seus vértices adjacentes até que ele atravessa todos os vértices visitados e tem que retroceder novamente. Desta forma, ele percorrerá todos os vértices alcançáveis do vértice inicial $ v $.

DFS Algorithm

O conceito é visitar todos os vértices vizinhos de um vértice vizinho antes de visitar os outros vértices vizinhos.

Inicializar o status de todos os nós como “Pronto”
Coloque o vértice de origem em uma pilha e mude seu status para "Esperando"
Repita as duas etapas a seguir até que a pilha esteja vazia -
- Destaque o vértice superior da pilha e marque-o como “Visitado”
- Empurre para o topo da pilha todos os vizinhos do vértice removido cujo status é “Pronto”. Marque seu status como “Esperando”.

Problem

Vamos pegar um gráfico (o vértice de origem é 'a') e aplicar o algoritmo DFS para descobrir a ordem de travessia.

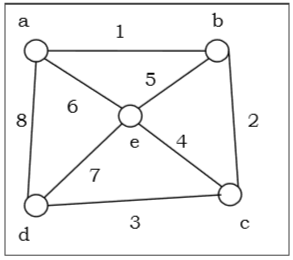
Solution

Inicialize o status de todos os vértices para “Pronto”.
Coloque um na pilha e altere seu status para “Esperando”.
Abra um e marque-o como “Visitado”.
Empurre a vizinhos ‘s em‘Ready’estado e, d e b ao topo da pilha e marcá-los como‘espera’.
Retire b da pilha, marque-o como “Visitado” e empurre seu vizinho “Pronto” c para a pilha.
Retire c da pilha e marque-a como “Visitada”. Não tem vizinho “pronto”.
Pop d de pilha e marcá-lo como “visitou”. Não tem vizinho “pronto”.
Pop e de pilha e marcá-lo como “visitou”. Não tem vizinho “pronto”.
A pilha está vazia. Então para.

Portanto, a ordem de passagem é -

$ a \ rightarrow b \ rightarrow c \ rightarrow d \ rightarrow e $

As ordens alternativas de travessia são -

$ a \ rightarrow e \ rightarrow b \ rightarrow c \ rightarrow d $

Ou $ a \ rightarrow b \ rightarrow e \ rightarrow c \ rightarrow d $

Ou $ a \ rightarrow d \ rightarrow e \ rightarrow b \ rightarrow c $

Ou $ a \ rightarrow d \ rightarrow c \ rightarrow e \ rightarrow b $

Ou $ a \ rightarrow d \ rightarrow c \ rightarrow b \ rightarrow e $

Complexity Analysis

Seja $ G (V, E) $ um gráfico com $ | V | $ número de vértices e $ | E | $ número de arestas. Se o algoritmo DFS visitar todos os vértices do gráfico e verificar todas as arestas, a complexidade do tempo é -

$$ \ circleddash (| V | + | E |) $$

Applications

Detecção de ciclo em um gráfico
Para encontrar classificação topológica
Para testar se um gráfico é bipartido
Localizando componentes conectados
Encontrando as pontes de um gráfico
Encontrar bi-conectividade em gráficos
Resolvendo o problema do Knight's Tour
Resolvendo quebra-cabeças com apenas uma solução