Aprendizado de máquina - habilidades
O aprendizado de máquina tem uma largura muito grande e requer habilidades em vários domínios. As habilidades que você precisa adquirir para se tornar um especialista em Aprendizado de Máquina estão listadas abaixo -
- Statistics
- Teorias de Probabilidade
- Calculus
- Técnicas de otimização
- Visualization
Necessidade de várias habilidades de aprendizado de máquina
Para lhe dar uma breve ideia de quais habilidades você precisa adquirir, vamos discutir alguns exemplos -
Notação Matemática
A maioria dos algoritmos de aprendizado de máquina é fortemente baseada em matemática. O nível de matemática que você precisa saber é provavelmente apenas um nível de iniciante. O importante é que você seja capaz de ler a notação que os matemáticos usam em suas equações. Por exemplo, se você for capaz de ler a notação e compreender o que ela significa, você está pronto para aprender o aprendizado de máquina. Caso contrário, você pode precisar aprimorar seus conhecimentos de matemática.
$$ f_ {AN} (net- \ theta) = \ begin {cases} \ gamma & if \: net- \ theta \ geq \ epsilon \\ net- \ theta & if - \ epsilon <net- \ theta <\ epsilon \\ - \ gamma & if \: net- \ theta \ leq- \ epsilon \ end {cases} $$
$$ \ displaystyle \\\ max \ limits _ {\ alpha} \ begin {bmatrix} \ displaystyle \ sum \ limits_ {i = 1} ^ m \ alpha- \ frac {1} {2} \ displaystyle \ sum \ limits_ { i, j = 1} ^ m rótulo ^ \ left (\ begin {array} {c} i \\ \ end {array} \ right) \ cdot \: label ^ \ left (\ begin {array} {c} j \\ \ end {array} \ right) \ cdot \: a_ {i} \ cdot \: a_ {j} \ langle x ^ \ left (\ begin {array} {c} i \\ \ end {array} \ direita), x ^ \ left (\ begin {array} {c} j \\ \ end {array} \ right) \ rangle \ end {bmatrix} $$
$$ f_ {AN} (net- \ theta) = \ left (\ frac {e ^ {\ lambda (net- \ theta)} - e ^ {- \ lambda (net- \ theta)}} {e ^ { \ lambda (net- \ theta)} + e ^ {- \ lambda (net- \ theta)}} \ right) \; $$
Teoria da probabilidade
Aqui está um exemplo para testar seu conhecimento atual da teoria da probabilidade: Classificação com probabilidades condicionais.
$$ p (c_ {i} | x, y) \; = \ frac {p (x, y | c_ {i}) \; p (c_ {i}) \;} {p (x, y) \ ;} $$
Com essas definições, podemos definir a regra de classificação Bayesiana -
- Se P (c1 | x, y)> P (c2 | x, y), a classe é c1.
- Se P (c1 | x, y) <P (c2 | x, y), a classe é c2.
Problema de Otimização
Aqui está uma função de otimização
$$ \ displaystyle \\\ max \ limits _ {\ alpha} \ begin {bmatrix} \ displaystyle \ sum \ limits_ {i = 1} ^ m \ alpha- \ frac {1} {2} \ displaystyle \ sum \ limits_ { i, j = 1} ^ m rótulo ^ \ left (\ begin {array} {c} i \\ \ end {array} \ right) \ cdot \: label ^ \ left (\ begin {array} {c} j \\ \ end {array} \ right) \ cdot \: a_ {i} \ cdot \: a_ {j} \ langle x ^ \ left (\ begin {array} {c} i \\ \ end {array} \ direita), x ^ \ left (\ begin {array} {c} j \\ \ end {array} \ right) \ rangle \ end {bmatrix} $$
Sujeito às seguintes restrições -
$$ \ alpha \ geq0 e \: \ displaystyle \ sum \ limits_ {i-1} ^ m \ alpha_ {i} \ cdot \: rótulo ^ \ left (\ begin {array} {c} i \\ \ end {array} \ right) = 0 $$
Se você pode ler e entender o acima, está tudo pronto.
Visualização
Em muitos casos, você precisará entender os vários tipos de gráficos de visualização para entender a distribuição dos dados e interpretar os resultados da saída do algoritmo.
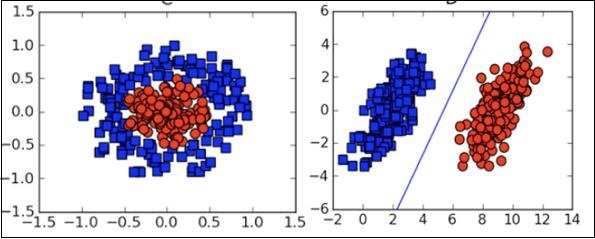
Além dos aspectos teóricos acima do aprendizado de máquina, você precisa de boas habilidades de programação para codificar esses algoritmos.
Então, o que é necessário para implementar o ML? Vamos examinar isso no próximo capítulo.