MATLAB - Integração
A integração lida com dois tipos de problemas essencialmente diferentes.
No primeiro tipo, a derivada de uma função é fornecida e queremos encontrar a função. Portanto, basicamente invertemos o processo de diferenciação. Este processo reverso é conhecido como antidiferenciação, ou encontrar a função primitiva, ou encontrar umindefinite integral.
O segundo tipo de problema envolve somar um número muito grande de quantidades muito pequenas e, então, estabelecer um limite conforme o tamanho das quantidades se aproxima de zero, enquanto o número de termos tende ao infinito. Este processo leva à definição dodefinite integral.
Integrais definidos são usados para encontrar área, volume, centro de gravidade, momento de inércia, trabalho realizado por uma força e em inúmeras outras aplicações.
Encontrando Integral Indefinido Usando MATLAB
Por definição, se a derivada de uma função f (x) é f '(x), então dizemos que uma integral indefinida de f' (x) em relação a x é f (x). Por exemplo, como a derivada (em relação a x) de x 2 é 2x, podemos dizer que uma integral indefinida de 2x é x 2 .
Em símbolos -
f'(x2) = 2x, Portanto,
∫ 2xdx = x2.
A integral indefinida não é única, porque a derivada de x 2 + c, para qualquer valor de uma constante c, também será 2x.
Isso é expresso em símbolos como -
∫ 2xdx = x2 + c.
Onde, c é chamado de 'constante arbitrária'.
O MATLAB fornece um intcomando para calcular a integral de uma expressão. Para derivar uma expressão para a integral indefinida de uma função, escrevemos -
int(f);Por exemplo, do nosso exemplo anterior -
syms x
int(2*x)O MATLAB executa a instrução acima e retorna o seguinte resultado -
ans =
x^2Exemplo 1
Neste exemplo, vamos encontrar a integral de algumas expressões comumente usadas. Crie um arquivo de script e digite o seguinte código nele -
syms x n
int(sym(x^n))
f = 'sin(n*t)'
int(sym(f))
syms a t
int(a*cos(pi*t))
int(a^x)Quando você executa o arquivo, ele exibe o seguinte resultado -
ans =
piecewise([n == -1, log(x)], [n ~= -1, x^(n + 1)/(n + 1)])
f =
sin(n*t)
ans =
-cos(n*t)/n
ans =
(a*sin(pi*t))/pi
ans =
a^x/log(a)Exemplo 2
Crie um arquivo de script e digite o seguinte código nele -
syms x n
int(cos(x))
int(exp(x))
int(log(x))
int(x^-1)
int(x^5*cos(5*x))
pretty(int(x^5*cos(5*x)))
int(x^-5)
int(sec(x)^2)
pretty(int(1 - 10*x + 9 * x^2))
int((3 + 5*x -6*x^2 - 7*x^3)/2*x^2)
pretty(int((3 + 5*x -6*x^2 - 7*x^3)/2*x^2))Observe que o pretty função retorna uma expressão em um formato mais legível.
Quando você executa o arquivo, ele exibe o seguinte resultado -
ans =
sin(x)
ans =
exp(x)
ans =
x*(log(x) - 1)
ans =
log(x)
ans =
(24*cos(5*x))/3125 + (24*x*sin(5*x))/625 - (12*x^2*cos(5*x))/125 + (x^4*cos(5*x))/5 - (4*x^3*sin(5*x))/25 + (x^5*sin(5*x))/5
2 4
24 cos(5 x) 24 x sin(5 x) 12 x cos(5 x) x cos(5 x)
----------- + ------------- - -------------- + ------------
3125 625 125 5
3 5
4 x sin(5 x) x sin(5 x)
------------- + -----------
25 5
ans =
-1/(4*x^4)
ans =
tan(x)
2
x (3 x - 5 x + 1)
ans =
- (7*x^6)/12 - (3*x^5)/5 + (5*x^4)/8 + x^3/2
6 5 4 3
7 x 3 x 5 x x
- ---- - ---- + ---- + --
12 5 8 2Encontrando Integral Definido Usando MATLAB
Por definição, integral definida é basicamente o limite de uma soma. Usamos integrais definidas para encontrar áreas como a área entre uma curva e o eixo xe a área entre duas curvas. Integrais definidos também podem ser usados em outras situações, onde a quantidade necessária pode ser expressa como o limite de uma soma.
o int A função pode ser usada para integração definida, passando os limites sobre os quais você deseja calcular a integral.
Calcular
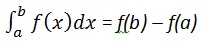
nós escrevemos,
int(x, a, b)Por exemplo, para calcular o valor de

int(x, 4, 9)O MATLAB executa a instrução acima e retorna o seguinte resultado -
ans =
65/2A seguir está o equivalente do Octave do cálculo acima -
pkg load symbolic
symbols
x = sym("x");
f = x;
c = [1, 0];
integral = polyint(c);
a = polyval(integral, 9) - polyval(integral, 4);
display('Area: '), disp(double(a));O Octave executa o código e retorna o seguinte resultado -
Area:
32.500Uma solução alternativa pode ser dada usando a função quad () fornecida pelo Octave como segue -
pkg load symbolic
symbols
f = inline("x");
[a, ierror, nfneval] = quad(f, 4, 9);
display('Area: '), disp(double(a));O Octave executa o código e retorna o seguinte resultado -
Area:
32.500Exemplo 1
Vamos calcular a área delimitada entre o eixo xe a curva y = x 3 −2x + 5 e as ordenadas x = 1 e x = 2.
A área necessária é fornecida por -
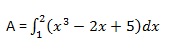
Crie um arquivo de script e digite o seguinte código -
f = x^3 - 2*x +5;
a = int(f, 1, 2)
display('Area: '), disp(double(a));Quando você executa o arquivo, ele exibe o seguinte resultado -
a =
23/4
Area:
5.7500A seguir está o equivalente do Octave do cálculo acima -
pkg load symbolic
symbols
x = sym("x");
f = x^3 - 2*x +5;
c = [1, 0, -2, 5];
integral = polyint(c);
a = polyval(integral, 2) - polyval(integral, 1);
display('Area: '), disp(double(a));O Octave executa o código e retorna o seguinte resultado -
Area:
5.7500Uma solução alternativa pode ser dada usando a função quad () fornecida pelo Octave como segue -
pkg load symbolic
symbols
x = sym("x");
f = inline("x^3 - 2*x +5");
[a, ierror, nfneval] = quad(f, 1, 2);
display('Area: '), disp(double(a));O Octave executa o código e retorna o seguinte resultado -
Area:
5.7500Exemplo 2
Encontre a área sob a curva: f (x) = x 2 cos (x) para −4 ≤ x ≤ 9.
Crie um arquivo de script e escreva o seguinte código -
f = x^2*cos(x);
ezplot(f, [-4,9])
a = int(f, -4, 9)
disp('Area: '), disp(double(a));Quando você executa o arquivo, o MATLAB traça o gráfico -
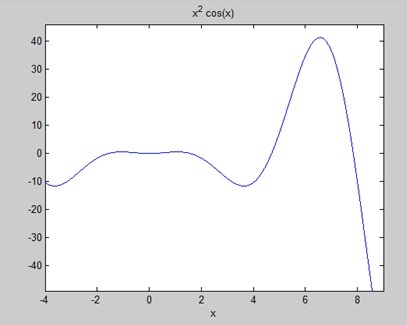
O resultado é dado abaixo -
a =
8*cos(4) + 18*cos(9) + 14*sin(4) + 79*sin(9)
Area:
0.3326A seguir está o equivalente do Octave do cálculo acima -
pkg load symbolic
symbols
x = sym("x");
f = inline("x^2*cos(x)");
ezplot(f, [-4,9])
print -deps graph.eps
[a, ierror, nfneval] = quad(f, -4, 9);
display('Area: '), disp(double(a));