MATLAB - Guia Rápido

MATLAB (matrix Laboratory) é uma linguagem de programação de alto nível de quarta geração e ambiente interativo para computação numérica, visualização e programação.

MATLAB é desenvolvido pela MathWorks.

Permite manipulações de matrizes; plotagem de funções e dados; implementação de algoritmos; criação de interfaces de usuário; interface com programas escritos em outras linguagens, incluindo C, C ++, Java e FORTRAN; analisar dados; desenvolver algoritmos; e criar modelos e aplicativos.

Possui vários comandos embutidos e funções matemáticas que o ajudam em cálculos matemáticos, geração de gráficos e execução de métodos numéricos.

O Poder da Matemática Computacional do MATLAB

O MATLAB é usado em todas as facetas da matemática computacional. A seguir estão alguns cálculos matemáticos comumente usados, onde é mais comumente usado -

Lidando com matrizes e matrizes
Plotagem e gráficos 2-D e 3-D
Álgebra Linear
Equações Algébricas
Funções não lineares
Statistics
Análise de dados
Cálculo e equações diferenciais
Cálculos Numéricos
Integration
Transforms
Ajuste de curva
Várias outras funções especiais

Características do MATLAB

A seguir estão os recursos básicos do MATLAB -

É uma linguagem de alto nível para computação numérica, visualização e desenvolvimento de aplicativos.
Ele também fornece um ambiente interativo para exploração iterativa, design e solução de problemas.
Ele fornece uma vasta biblioteca de funções matemáticas para álgebra linear, estatística, análise de Fourier, filtragem, otimização, integração numérica e solução de equações diferenciais ordinárias.
Ele fornece gráficos integrados para visualizar dados e ferramentas para criar plotagens personalizadas.
A interface de programação do MATLAB oferece ferramentas de desenvolvimento para melhorar a capacidade de manutenção da qualidade do código e maximizar o desempenho.
Ele fornece ferramentas para construir aplicativos com interfaces gráficas personalizadas.
Ele fornece funções para integrar algoritmos baseados em MATLAB com aplicativos e linguagens externas, como C, Java, .NET e Microsoft Excel.

Usos do MATLAB

O MATLAB é amplamente utilizado como ferramenta computacional na ciência e engenharia, abrangendo os campos da física, química, matemática e todos os ramos da engenharia. É usado em uma variedade de aplicações, incluindo -

Processamento de Sinal e Comunicações
Processamento de imagem e vídeo
Sistemas de controle
Teste e Medição
Finanças Computacionais
Biologia Computacional

Configuração de ambiente local

Configurar o ambiente MATLAB é questão de poucos cliques. O instalador pode ser baixado aqui .

MathWorks fornece o produto licenciado, uma versão de teste e uma versão de estudante também. Você precisa se logar no site e aguardar um pouco a aprovação deles.

Depois de baixar o instalador, o software pode ser instalado com alguns cliques.

Compreendendo o ambiente MATLAB

O IDE de desenvolvimento MATLAB pode ser iniciado a partir do ícone criado na área de trabalho. A janela principal de trabalho do MATLAB é chamada de área de trabalho. Quando o MATLAB é iniciado, a área de trabalho aparece em seu layout padrão -

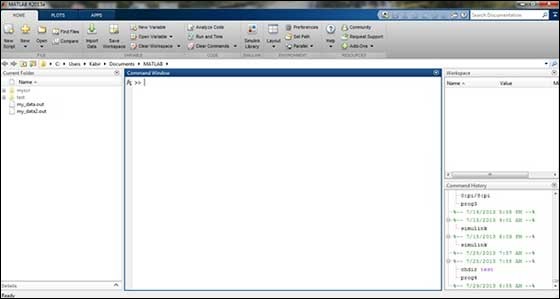
A área de trabalho possui os seguintes painéis -

Current Folder - Este painel permite que você acesse as pastas e arquivos do projeto.

Command Window- Esta é a área principal onde os comandos podem ser inseridos na linha de comando. É indicado pelo prompt de comando (>>).

Workspace - A área de trabalho mostra todas as variáveis criadas e / ou importadas de arquivos.

Command History - Este painel mostra ou retorna comandos que são inseridos na linha de comando.

Configurar GNU Octave

Se você deseja usar o Octave em sua máquina (Linux, BSD, OS X ou Windows), faça o download da versão mais recente em Baixe o GNU Octave . Você pode verificar as instruções de instalação fornecidas para sua máquina.

O ambiente MATLAB se comporta como uma calculadora supercomplexa. Você pode inserir comandos no >> prompt de comando.

MATLAB é um ambiente interpretado. Em outras palavras, você dá um comando e o MATLAB o executa imediatamente.

Prática Prática

Digite uma expressão válida, por exemplo,

5 + 5

E pressione ENTER

Ao clicar no botão Executar ou digitar Ctrl + E, o MATLAB o executa imediatamente e o resultado retornado é -

ans = 10

Vamos pegar mais alguns exemplos -

3 ^ 2	       % 3 raised to the power of 2

Ao clicar no botão Executar ou digitar Ctrl + E, o MATLAB o executa imediatamente e o resultado retornado é -

ans = 9

Outro exemplo,

sin(pi /2)	  % sine of angle 90^o

Ao clicar no botão Executar ou digitar Ctrl + E, o MATLAB o executa imediatamente e o resultado retornado é -

ans = 1

Outro exemplo,

7/0		      % Divide by zero

Ao clicar no botão Executar ou digitar Ctrl + E, o MATLAB o executa imediatamente e o resultado retornado é -

ans = Inf
warning: division by zero

Outro exemplo,

732 * 20.3

Ao clicar no botão Executar ou digitar Ctrl + E, o MATLAB o executa imediatamente e o resultado retornado é -

ans =  1.4860e+04

O MATLAB fornece algumas expressões especiais para alguns símbolos matemáticos, como pi para π, Inf para ∞, i (e j) para √-1 etc. Nan significa 'não é um número'.

Uso do ponto e vírgula (;) no MATLAB

Ponto-e-vírgula (;) indica o fim da declaração. No entanto, se você deseja suprimir e ocultar a saída do MATLAB para uma expressão, adicione um ponto-e-vírgula após a expressão.

Por exemplo,

x = 3;
y = x + 5

Ao clicar no botão Executar ou digitar Ctrl + E, o MATLAB o executa imediatamente e o resultado retornado é -

y =  8

Adicionando comentários

O símbolo de porcentagem (%) é usado para indicar uma linha de comentário. Por exemplo,

x = 9	     % assign the value 9 to x

Você também pode escrever um bloco de comentários usando os operadores de bloco de comentários% {e%}.

O editor MATLAB inclui ferramentas e itens de menu de contexto para ajudá-lo a adicionar, remover ou alterar o formato dos comentários.

Operadores e caracteres especiais comumente usados

O MATLAB suporta os seguintes operadores e caracteres especiais comumente usados -

Operador	Objetivo
+	Mais; operador de adição.
-	Menos; operador de subtração.
*	Operador de multiplicação escalar e matricial.
.*	Operador de multiplicação de matriz.
^	Operador de exponenciação escalar e matricial.
.^	Operador de exponenciação de matriz.
\	Operador de divisão à esquerda.
/	Operador de divisão à direita.
.\	Operador de divisão à esquerda da matriz.
./	Operador de divisão à direita do array.
:	Cólon; gera elementos regularmente espaçados e representa uma linha ou coluna inteira.
( )	Parênteses; inclui argumentos de função e índices de matriz; substitui a precedência.
[ ]	Suportes; inclui elementos da matriz.
.	Ponto decimal.
…	Elipse; operador de continuação de linha
,	Vírgula; separa instruções e elementos em uma linha
;	Ponto e vírgula; separa colunas e suprime a exibição.
%	Sinal de porcentagem; designa um comentário e especifica a formatação.
_	Cite o sinal e transponha o operador.
._	Operador de transposição não conjugado.
=	Operador de atribuição.

Variáveis e constantes especiais

O MATLAB suporta as seguintes variáveis e constantes especiais -

Nome	Significado
ans	Resposta mais recente.
eps	Exatidão da precisão de ponto flutuante.
i,j	A unidade imaginária √-1.
Inf	Infinidade.
NaN	Resultado numérico indefinido (não é um número).
pi	O número π

Nomeando Variáveis

Os nomes das variáveis consistem em uma letra seguida por qualquer número de letras, dígitos ou sublinhados.

MATLAB é case-sensitive.

Os nomes das variáveis podem ter qualquer comprimento, no entanto, o MATLAB usa apenas os primeiros N caracteres, onde N é dado pela função namelengthmax.

Salvando Seu Trabalho

o save comando é usado para salvar todas as variáveis na área de trabalho, como um arquivo com extensão .mat, no diretório atual.

Por exemplo,

save myfile

Você pode recarregar o arquivo a qualquer momento mais tarde usando o load comando.

load myfile

No ambiente MATLAB, cada variável é um array ou matriz.

Você pode atribuir variáveis de uma maneira simples. Por exemplo,

x = 3	       % defining x and initializing it with a value

O MATLAB executará a instrução acima e retornará o seguinte resultado -

x = 3

Ele cria uma matriz 1 por 1 denominada x e armazena o valor 3 em seu elemento. Vamos verificar outro exemplo,

x = sqrt(16) 	% defining x and initializing it with an expression

O MATLAB executará a instrução acima e retornará o seguinte resultado -

x = 4

Observe que -

Depois que uma variável é inserida no sistema, você pode consultá-la mais tarde.
As variáveis devem ter valores antes de serem usadas.
Quando uma expressão retorna um resultado que não está atribuído a nenhuma variável, o sistema o atribui a uma variável chamada ans, que pode ser usada posteriormente.

Por exemplo,

sqrt(78)

O MATLAB executará a instrução acima e retornará o seguinte resultado -

ans =  8.8318

Você pode usar esta variável ans -

sqrt(78);
9876/ans

O MATLAB executará a instrução acima e retornará o seguinte resultado -

ans =  1118.2

Vejamos outro exemplo -

x = 7 * 8;
y = x * 7.89

O MATLAB executará a instrução acima e retornará o seguinte resultado -

y =  441.84

Múltiplas atribuições

Você pode ter várias atribuições na mesma linha. Por exemplo,

a = 2; b = 7; c = a * b

O MATLAB executará a instrução acima e retornará o seguinte resultado -

c = 14

Esqueci as variáveis!

o who comando exibe todos os nomes de variáveis que você usou.

who

O MATLAB executará a instrução acima e retornará o seguinte resultado -

Your variables are:
a    ans  b    c

o whos comando exibe um pouco mais sobre as variáveis -

Variáveis atualmente na memória
Tipo de cada variável
Memória alocada para cada variável
Se são variáveis complexas ou não

whos

O MATLAB executará a instrução acima e retornará o seguinte resultado -

Attr Name        Size        Bytes      Class
==== ====        ====        ====       ===== 
   a             1x1           8        double
   ans           1x70         757        cell
   b             1x1           8        double
   c             1x1           8        double

Total is 73 elements using 781 bytes

o clear comando exclui todas (ou as variáveis especificadas) da memória.

clear x     % it will delete x, won't display anything
clear       % it will delete all variables in the workspace
            %  peacefully and unobtrusively

Longas atribuições

Atribuições longas podem ser estendidas para outra linha usando reticências (...). Por exemplo,

initial_velocity = 0;
acceleration = 9.8;
time = 20;
final_velocity = initial_velocity + acceleration * time

O MATLAB executará a instrução acima e retornará o seguinte resultado -

final_velocity = 196

O formato Comando

Por padrão, o MATLAB exibe números com quatro valores de casas decimais. Isso é conhecido comoshort format.

No entanto, se quiser mais precisão, você precisa usar o format comando.

o format long comando exibe 16 dígitos após o decimal.

Por exemplo -

format long
x = 7 + 10/3 + 5 ^ 1.2

O MATLAB irá executar a instrução acima e retornar o seguinte resultado -

x = 17.2319816406394

Outro exemplo,

format short
x = 7 + 10/3 + 5 ^ 1.2

O MATLAB executará a instrução acima e retornará o seguinte resultado -

x = 17.232

o format bankcomando arredonda os números para duas casas decimais. Por exemplo,

format bank
daily_wage = 177.45;
weekly_wage = daily_wage * 6

O MATLAB executará a instrução acima e retornará o seguinte resultado -

weekly_wage = 1064.70

O MATLAB exibe números grandes usando notação exponencial.

o format short e comando permite exibir em forma exponencial com quatro casas decimais mais o expoente.

Por exemplo,

format short e
4.678 * 4.9

O MATLAB executará a instrução acima e retornará o seguinte resultado -

ans = 2.2922e+01

o format long ecomando permite exibir em forma exponencial com quatro casas decimais mais o expoente. Por exemplo,

format long e
x = pi

O MATLAB executará a instrução acima e retornará o seguinte resultado -

x = 3.141592653589793e+00

o format ratcomando fornece a expressão racional mais próxima resultante de um cálculo. Por exemplo,

format rat
4.678 * 4.9

O MATLAB executará a instrução acima e retornará o seguinte resultado -

ans = 34177/1491

Criação de vetores

Um vetor é uma matriz unidimensional de números. O MATLAB permite a criação de dois tipos de vetores -

Vetores de linha
Vetores coluna

Row vectors são criados colocando o conjunto de elementos entre colchetes, usando espaço ou vírgula para delimitar os elementos.

Por exemplo,

r = [7 8 9 10 11]

O MATLAB executará a instrução acima e retornará o seguinte resultado -

r =

   7    8    9   10   11

Outro exemplo,

r = [7 8 9 10 11];
t = [2, 3, 4, 5, 6];
res = r + t

O MATLAB executará a instrução acima e retornará o seguinte resultado -

res =

         9         11         13         15         17

Column vectors são criados colocando o conjunto de elementos entre colchetes, usando ponto e vírgula (;) para delimitar os elementos.

c = [7;  8;  9;  10; 11]

O MATLAB executará a instrução acima e retornará o seguinte resultado -

Criação de matrizes

Uma matriz é uma matriz bidimensional de números.

No MATLAB, uma matriz é criada inserindo cada linha como uma sequência de espaço ou elementos separados por vírgula, e o final de uma linha é demarcado por um ponto e vírgula. Por exemplo, vamos criar uma matriz 3 por 3 como -

m = [1 2 3; 4 5 6; 7 8 9]

O MATLAB executará a instrução acima e retornará o seguinte resultado -

m =
       1              2              3       
       4              5              6       
       7              8              9

MATLAB é um programa interativo para computação numérica e visualização de dados. Você pode inserir um comando digitando-o no prompt do MATLAB '>>' noCommand Window.

Nesta seção, forneceremos listas de comandos gerais do MATLAB comumente usados.

Comandos para gerenciar uma sessão

O MATLAB fornece vários comandos para gerenciar uma sessão. A tabela a seguir fornece todos esses comandos -

Comando	Objetivo
clc	Limpa a janela de comando.
Claro	Remove variáveis da memória.
existir	Verifica a existência de arquivo ou variável.
global	Declara as variáveis como globais.
Socorro	Procura um tópico de ajuda.
olhe para	Pesquisa entradas de ajuda para uma palavra-chave.
Sair	Pára o MATLAB.
quem	Lista as variáveis atuais.
quem é	Lista as variáveis atuais (tela longa).

Comandos para trabalhar com o sistema

O MATLAB fornece vários comandos úteis para trabalhar com o sistema, como salvar o trabalho atual na área de trabalho como um arquivo e carregar o arquivo posteriormente.

Ele também fornece vários comandos para outras atividades relacionadas ao sistema, como exibição de data, listagem de arquivos no diretório, exibição do diretório atual, etc.

A tabela a seguir exibe alguns comandos relacionados ao sistema comumente usados -

Comando	Objetivo
CD	Muda o diretório atual.
encontro	Exibe a data atual.
excluir	Exclui um arquivo.
diário	Liga / desliga a gravação do arquivo do diário.
dir	Lista todos os arquivos no diretório atual.
carga	Carrega variáveis de espaço de trabalho de um arquivo.
caminho	Exibe o caminho de pesquisa.
pwd	Exibe o diretório atual.
Salve 	Salva variáveis do espaço de trabalho em um arquivo.
tipo	Exibe o conteúdo de um arquivo.
o que	Lista todos os arquivos MATLAB no diretório atual.
wklread	Lê o arquivo de planilha .wk1.

Comandos de entrada e saída

O MATLAB fornece os seguintes comandos relacionados de entrada e saída -

Comando	Objetivo
disp	Exibe o conteúdo de uma matriz ou string.
fscanf	Leia os dados formatados de um arquivo.
formato	Controla o formato de exibição da tela.
fprintf	Executa gravações formatadas na tela ou arquivo.
entrada	Exibe prompts e espera por entrada.
;	Suprime a impressão da tela.

o fscanf e fprintfos comandos se comportam como funções C scanf e printf. Eles suportam os seguintes códigos de formato -

Código de Formato	Objetivo
%s	Formate como uma string.
%d	Formate como um inteiro.
%f	Formate como um valor de ponto flutuante.
%e	Formate como um valor de ponto flutuante em notação científica.
%g	Formato na forma mais compacta:% f ou% e.
\n	Insira uma nova linha na string de saída.
\t	Insira uma guia na string de saída.

A função de formato tem os seguintes formatos usados para exibição numérica -

Função de Formato	Exibir até
formato curto	Quatro dígitos decimais (padrão).
formato longo	16 dígitos decimais.
formato curto e	Cinco dígitos mais expoente.
formato longo e	16 dígitos mais expoentes.
banco de formato	Dois dígitos decimais.
formato +	Positivo, negativo ou zero.
formatar rato	Aproximação racional.
formato compacto	Suprime alguns avanços de linha.
formato solto	Redefine para o modo de exibição menos compacto.

Comandos de vetor, matriz e matriz

A tabela a seguir mostra vários comandos usados para trabalhar com matrizes, matrizes e vetores -

Comando	Objetivo
gato	Concatena matrizes.
encontrar	Encontra índices de elementos diferentes de zero.
comprimento	Calcula o número de elementos.
linspace	Cria vetores espaçados regularmente.
logspace	Cria vetor espaçado logaritmicamente.
max	Retorna o maior elemento.
min	Retorna o menor elemento.
aguilhão	Produto de cada coluna.
remodelar	Altera o tamanho.
Tamanho	Calcula o tamanho da matriz.
ordenar	Classifica cada coluna.
soma	Soma cada coluna.
olho	Cria uma matriz de identidade.
uns	Cria uma série de unidades.
zeros	Cria uma matriz de zeros.
Cruz	Calcula produtos cruzados da matriz.
ponto	Calcula produtos de ponto da matriz.
det	Calcula o determinante de uma matriz.
inv	Calcula o inverso de uma matriz.
pinv	Calcula o pseudoinverso de uma matriz.
classificação	Calcula a classificação de uma matriz.
rref	Calcula a forma escalonada de linha reduzida.
célula	Cria matriz de células.
celldisp	Exibe a matriz de células.
lote de células	Exibe uma representação gráfica da matriz de células.
num2cell	Converte matriz numérica em matriz de células.
lidar	Combina listas de entrada e saída.
iscell	Identifica a matriz de células.

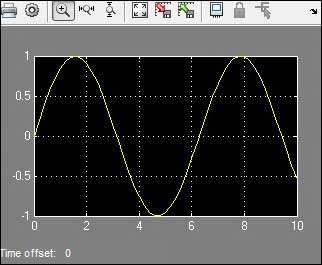
Comandos de plotagem

O MATLAB fornece vários comandos para plotar gráficos. A tabela a seguir mostra alguns dos comandos comumente usados para plotagem -

Comando	Objetivo
eixo	Define os limites do eixo.
fplot	Plotagem inteligente de funções.
rede	Exibe linhas de grade.
enredo	Gera o gráfico xy.
impressão	Imprime plotagem ou salva plotagem em um arquivo.
título	Coloca o texto no topo do gráfico.
xlabel	Adiciona rótulo de texto ao eixo x.
Ylabel	Adiciona rótulo de texto ao eixo y.
eixos	Cria objetos de eixos.
Fechar	Fecha o gráfico atual.
feche tudo	Fecha todos os lotes.
figura	Abre uma nova janela de figura.
gtext	Habilita o posicionamento do rótulo com o mouse.
aguarde	Congela o gráfico atual.
lenda	Posicionamento da legenda com o mouse.
refrescar	Redesenha a janela da figura atual.
conjunto	Especifica propriedades de objetos, como eixos.
subtrama	Cria gráficos em subjanelas.
texto	Coloca string na figura.
Barra	Cria gráfico de barras.
loglog	Cria um gráfico log-log.
polar	Cria um gráfico polar.
semilogx	Cria um gráfico semilog. (abscissa logarítmica).
semilogia	Cria um gráfico semilog. (ordenada logarítmica).
escadas	Cria o gráfico de escadas.
haste	Cria um gráfico de haste.

Até agora, usamos o ambiente MATLAB como calculadora. No entanto, MATLAB também é uma linguagem de programação poderosa, bem como um ambiente computacional interativo.

Nos capítulos anteriores, você aprendeu como inserir comandos no prompt de comando do MATLAB. O MATLAB também permite que você escreva uma série de comandos em um arquivo e execute o arquivo como uma unidade completa, como escrever uma função e chamá-la.

The M Files

O MATLAB permite escrever dois tipos de arquivos de programa -

Scripts - arquivos de script são arquivos de programa com .m extension. Nestes arquivos, você escreve uma série de comandos, que deseja executar juntos. Scripts não aceitam entradas e não retornam nenhuma saída. Eles operam em dados no espaço de trabalho.
Functions - arquivos de funções também são arquivos de programa com .m extension. As funções podem aceitar entradas e retornar saídas. Variáveis internas são locais para a função.

Você pode usar o editor MATLAB ou qualquer outro editor de texto para criar seu .marquivos. Nesta seção, discutiremos os arquivos de script. Um arquivo de script contém várias linhas sequenciais de comandos MATLAB e chamadas de função. Você pode executar um script digitando seu nome na linha de comando.

Criação e execução de arquivo de script

Para criar arquivos de script, você precisa usar um editor de texto. Você pode abrir o editor MATLAB de duas maneiras -

Usando o prompt de comando
Usando o IDE

Se você estiver usando o prompt de comando, digite editno prompt de comando. Isso abrirá o editor. Você pode digitar diretamenteedit e o nome do arquivo (com extensão .m)

edit 
Or
edit <filename>

O comando acima criará o arquivo no diretório padrão do MATLAB. Se você deseja armazenar todos os arquivos de programa em uma pasta específica, deverá fornecer o caminho completo.

Vamos criar uma pasta chamada progs. Digite os seguintes comandos no prompt de comando (>>) -

mkdir progs    % create directory progs under default directory
chdir progs    % changing the current directory to progs
edit  prog1.m  % creating an m file named prog1.m

Se você estiver criando o arquivo pela primeira vez, o MATLAB solicitará que você confirme. Clique em Sim.

Alternativamente, se você estiver usando o IDE, escolha NOVO -> Script. Isso também abre o editor e cria um arquivo denominado Sem título. Você pode nomear e salvar o arquivo após digitar o código.

Digite o seguinte código no editor -

NoOfStudents = 6000;
TeachingStaff = 150;
NonTeachingStaff = 20;
Total = NoOfStudents + TeachingStaff ...
   + NonTeachingStaff;
disp(Total);

Depois de criar e salvar o arquivo, você pode executá-lo de duas maneiras -

Clicar no Run botão na janela do editor ou
Basta digitar o nome do arquivo (sem extensão) no prompt de comando: >> prog1

O prompt da janela de comando exibe o resultado -

Exemplo

Crie um arquivo de script e digite o seguinte código -

a = 5; b = 7;
c = a + b
d = c + sin(b)
e = 5 * d
f = exp(-d)

Quando o código acima é compilado e executado, ele produz o seguinte resultado -

c =  12
d =  12.657
e =  63.285
f =    3.1852e-06

O MATLAB não requer nenhuma declaração de tipo ou declarações de dimensão. Sempre que o MATLAB encontra um novo nome de variável, ele cria a variável e aloca o espaço de memória apropriado.

Se a variável já existe, o MATLAB substitui o conteúdo original por um novo conteúdo e aloca novo espaço de armazenamento, quando necessário.

Por exemplo,

Total = 42

A declaração acima cria uma matriz 1 por 1 chamada 'Total' e armazena o valor 42 nela.

Tipos de dados disponíveis no MATLAB

O MATLAB fornece 15 tipos de dados fundamentais. Cada tipo de dados armazena dados que estão na forma de uma matriz ou array. O tamanho desta matriz ou array é no mínimo 0 por 0 e isso pode crescer até uma matriz ou array de qualquer tamanho.

A tabela a seguir mostra os tipos de dados mais comumente usados no MATLAB -

Sr. Não.	Tipo de dados e descrição
1	int8 Inteiro assinado de 8 bits
2	uint8 Inteiro sem sinal de 8 bits
3	int16 Inteiro assinado de 16 bits
4	uint16 Inteiro não assinado de 16 bits
5	int32 Inteiro assinado de 32 bits
6	uint32 Inteiro sem sinal de 32 bits
7	int64 Inteiro assinado de 64 bits
8	uint64 Inteiro não assinado de 64 bits
9	single dados numéricos de precisão única
10	double dados numéricos de dupla precisão
11	logical valores lógicos de 1 ou 0 representam verdadeiro e falso, respectivamente
12	char dados de caracteres (strings são armazenadas como vetores de caracteres)
13	cell array matriz de células indexadas, cada uma capaz de armazenar uma matriz de diferentes dimensões e tipos de dados
14	structure Estruturas semelhantes a C, cada estrutura tendo campos nomeados capazes de armazenar uma matriz de uma dimensão e tipo de dados diferente
15	function handle ponteiro para uma função
16	user classes objetos construídos a partir de uma classe definida pelo usuário
17	java classes objetos construídos a partir de uma classe Java

Exemplo

Crie um arquivo de script com o seguinte código -

str = 'Hello World!'
n = 2345
d = double(n)
un = uint32(789.50)
rn = 5678.92347
c = int32(rn)

Quando o código acima é compilado e executado, ele produz o seguinte resultado -

str = Hello World!
n =  2345
d =  2345
un = 790
rn = 5678.9
c =  5679

Conversão de Tipo de Dados

O MATLAB fornece várias funções para conversão de um valor de um tipo de dados para outro. A tabela a seguir mostra as funções de conversão de tipo de dados -

Função	Objetivo
Caracteres	Converter para matriz de caracteres (string)
int2str	Converter dados inteiros em string
mat2str	Converter matriz em string
num2str	Converter número em string
str2double	Converter string em valor de precisão dupla
str2num	Converter string em número
native2unicode	Converter bytes numéricos em caracteres Unicode
unicode2native	Converter caracteres Unicode em bytes numéricos
base2dec	Converte a sequência de números de base N em número decimal
bin2dec	Converter string de número binário em número decimal
dec2base	Converter decimal em número de base N na string
dec2bin	Converter decimal em número binário na string
dec2hex	Converter decimal em número hexadecimal na string
hex2dec	Converter string de número hexadecimal em número decimal
hex2num	Converter string de número hexadecimal em número de precisão dupla
num2hex	Converta singles e duplos em strings hexadecimais IEEE
cell2mat	Converter matriz de células em matriz numérica
cell2struct	Converter matriz de células em matriz de estrutura
cellstr	Crie uma matriz de células de strings a partir da matriz de caracteres
mat2cell	Converter array em array de células com células de tamanhos potencialmente diferentes
num2cell	Converta matriz em matriz de células com células de tamanho consistente
struct2cell	Converter estrutura em matriz de células

Determinação de tipos de dados

O MATLAB fornece várias funções para identificar o tipo de dados de uma variável.

A tabela a seguir fornece as funções para determinar o tipo de dados de uma variável -

Função	Objetivo
é	Detectar estado
é um	Determine se a entrada é um objeto da classe especificada
iscell	Determine se a entrada é uma matriz de células
iscellstr	Determine se a entrada é uma matriz de células de strings
ischar	Determine se o item é uma matriz de caracteres
Isfield	Determine se a entrada é um campo de matriz de estrutura
flutuar	Determine se a entrada é uma matriz de ponto flutuante
ishghandle	True para manipuladores de objeto de Handle Graphics
isinteger	Determine se a entrada é uma matriz de inteiros
isjava	Determine se a entrada é um objeto Java
islogical	Determine se a entrada é uma matriz lógica
isnumeric	Determine se a entrada é uma matriz numérica
isobjeto	Determine se a entrada é um objeto MATLAB
é real	Verifique se a entrada é uma matriz real
isscalar	Determine se a entrada é escalar
isstr	Determine se a entrada é uma matriz de caracteres
isstruct	Determine se a entrada é um array de estrutura
isvetor	Determine se a entrada é um vetor
classe	Determine a classe do objeto
atributos válidos	Verifique a validade da matriz
quem é	Listar variáveis na área de trabalho, com tamanhos e tipos

Exemplo

Crie um arquivo de script com o seguinte código -

x = 3
isinteger(x)
isfloat(x)
isvector(x)
isscalar(x)
isnumeric(x)
 
x = 23.54
isinteger(x)
isfloat(x)
isvector(x)
isscalar(x)
isnumeric(x)
 
x = [1 2 3]
isinteger(x)
isfloat(x)
isvector(x)
isscalar(x)
 
x = 'Hello'
isinteger(x)
isfloat(x)
isvector(x)
isscalar(x)
isnumeric(x)

Quando você executa o arquivo, ele produz o seguinte resultado -

x = 3
ans = 0
ans = 1
ans = 1
ans = 1
ans = 1
x = 23.540
ans = 0
ans = 1
ans = 1
ans = 1
ans = 1
x =

          1          2          3

ans = 0
ans = 1
ans = 1
ans = 0
x = Hello
ans = 0
ans = 0
ans = 1
ans = 0
ans = 0

Um operador é um símbolo que informa ao compilador para executar manipulações matemáticas ou lógicas específicas. O MATLAB é projetado para operar principalmente em matrizes e arrays inteiros. Portanto, os operadores no MATLAB trabalham com dados escalares e não escalares. O MATLAB permite os seguintes tipos de operações elementares -

Operadores aritméticos
Operadores Relacionais
Operadores lógicos
Operações bit a bit
Operações de conjunto

Operadores aritméticos

O MATLAB permite dois tipos diferentes de operações aritméticas -

Operações aritméticas de matriz
Operações aritméticas de matriz

As operações aritméticas de matriz são as mesmas definidas na álgebra linear. As operações de array são executadas elemento por elemento, em array unidimensional e multidimensional.

Os operadores de matriz e operadores de matriz são diferenciados pelo símbolo de ponto (.). No entanto, como a operação de adição e subtração é a mesma para matrizes e arrays, o operador é o mesmo para ambos os casos. A tabela a seguir fornece uma breve descrição dos operadores -

Mostrar exemplos

Sr. Não.	Operador e descrição
1	+ Adição ou adição unária. A + B adiciona os valores armazenados nas variáveis A e B. A e B devem ter o mesmo tamanho, a menos que um seja escalar. Um escalar pode ser adicionado a uma matriz de qualquer tamanho.
2	- Subtração ou menos unário. AB subtrai o valor de B de A. A e B devem ter o mesmo tamanho, a menos que um seja escalar. Um escalar pode ser subtraído de uma matriz de qualquer tamanho.
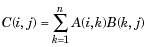
3	* Multiplicação da matriz. C = A * B é o produto algébrico linear das matrizes A e B. Mais precisamente, Para A e B não escalares, o número de colunas de A deve ser igual ao número de linhas de B. Um escalar pode multiplicar uma matriz de qualquer tamanho.
4	.* Multiplicação de matriz. A. * B é o produto elemento por elemento das matrizes A e B. A e B devem ter o mesmo tamanho, a menos que um deles seja escalar.
5	/ Corte ou divisão à direita da matriz. B / A é aproximadamente igual a B * inv (A). Mais precisamente, B / A = (A '\ B') '.
6	./ Array divisão certa. A./B é a matriz com os elementos A (i, j) / B (i, j). A e B devem ter o mesmo tamanho, a menos que um deles seja escalar.
7	\ Barra invertida ou divisão à esquerda da matriz. Se A é uma matriz quadrada, A \ B é aproximadamente o mesmo que inv (A) * B, exceto que é calculado de uma maneira diferente. Se A é um N-a-n matriz e B é um vector de coluna com n componentes, ou uma matriz com vários de tais colunas, então X = A \ B é a solução para a equação AX = B . Uma mensagem de aviso é exibida se A estiver mal dimensionado ou quase singular.
8	.\ Array deixou a divisão. A. \ B é a matriz com os elementos B (i, j) / A (i, j). A e B devem ter o mesmo tamanho, a menos que um deles seja escalar.
9	^ Poder da matriz. X ^ p é X elevado à potência p, se p for um escalar. Se p for um inteiro, a potência é calculada por quadratura repetida. Se o número inteiro for negativo, X será invertido primeiro. Para outros valores de p, o cálculo envolve autovalores e autovetores, de modo que se [V, D] = eig (X), então X ^ p = V * D. ^ p / V.
10	.^ Poder do array. A. ^ B é a matriz com os elementos A (i, j) à potência B (i, j). A e B devem ter o mesmo tamanho, a menos que um deles seja escalar.
11	' Transposição de matriz. A 'é a transposta algébrica linear de A. Para matrizes complexas, esta é a transposta conjugada complexa.
12	.' Transposição de matriz. UMA.' é a transposta da matriz de A. Para matrizes complexas, isso não envolve conjugação.

Operadores Relacionais

Os operadores relacionais também podem trabalhar com dados escalares e não escalares. Operadores relacionais para matrizes realizam comparações elemento por elemento entre duas matrizes e retornam uma matriz lógica do mesmo tamanho, com elementos definidos como 1 lógico (verdadeiro) onde a relação é verdadeira e elementos definidos como 0 lógico (falso) onde é não.

A tabela a seguir mostra os operadores relacionais disponíveis no MATLAB -

Mostrar exemplos

Sr. Não.	Operador e descrição
1	< Menor que
2	<= Menos que ou igual a
3	> Maior que
4	>= Melhor que ou igual a
5	== Igual a
6	~= Diferente de

Operadores lógicos

O MATLAB oferece dois tipos de operadores lógicos e funções -

Por elemento - esses operadores operam em elementos correspondentes de matrizes lógicas.
Curto-circuito - Esses operadores operam em expressões escalares e lógicas.

Operadores lógicos elemento a elemento operam elemento por elemento em matrizes lógicas. Os símbolos &, | e ~ são os operadores lógicos de matriz AND, OR e NOT.

Operadores lógicos de curto-circuito permitem curto-circuito em operações lógicas. Os símbolos && e || são os operadores lógicos de curto-circuito AND e OR.

Mostrar exemplos

Operações bit a bit

Operadores bit a bit trabalham em bits e executam operações bit a bit. As tabelas de verdade para &, | e ^ são as seguintes -

p	q	p & q	p \| q	p ^ q
0	0	0	0	0
0	1	0	1	1
1	1	1	1	0
1	0	0	1	1

Suponha que A = 60; e B = 13; Agora, em formato binário, eles serão os seguintes -

A = 0011 1100

B = 0000 1101

-----------------

A&B = 0000 1100

A | B = 0011 1101

A ^ B = 0011 0001

~ A = 1100 0011

O MATLAB fornece várias funções para operações bit a bit, como operações 'bit a bit e', 'bit a bit ou' e 'não bit a bit', operação de deslocamento, etc.

A tabela a seguir mostra as operações bit a bit comumente usadas -

Mostrar exemplos

Função	Objetivo
bitand (a, b)	E bit a bit de inteiros a e b
bitcmp (a)	Complemento bit-a-bit de um
bitget (a, pos)	Obtém o bit na posição especificada pos , na matriz de inteiros a
bitor (a, b)	OR bit a bit de inteiros a e b
bitset (a, pos)	Defina a broca na posição específica pos de um
bitshift (a, k)	Retorna a deslocado para a esquerda por k bits, equivalente a multiplicar por 2 ^k . Os valores negativos de k correspondem ao deslocamento dos bits à direita ou à divisão por 2 ^{\| k \|}e arredondamento para o número inteiro mais próximo para o infinito negativo. Quaisquer bits de estouro são truncados.
bitxor (a, b)	XOR bit a bit de inteiros a e b
swapbytes	Troca de ordem de byte

Operações de conjunto

O MATLAB fornece várias funções para operações de conjunto, como união, interseção e teste para associação de conjunto, etc.

A tabela a seguir mostra algumas operações de conjunto comumente usadas -

Mostrar exemplos

Sr. Não.	Descrição da função
1	intersect(A,B) Defina a interseção de duas matrizes; retorna os valores comuns a A e B. Os valores retornados estão em ordem de classificação.
2	intersect(A,B,'rows') Trata cada linha de A e cada linha de B como entidades únicas e retorna as linhas comuns a A e B. As linhas da matriz retornada estão em ordem de classificação.
3	ismember(A,B) Retorna uma matriz do mesmo tamanho de A, contendo 1 (verdadeiro) onde os elementos de A são encontrados em B. Em outro lugar, retorna 0 (falso).
4	ismember(A,B,'rows') Trata cada linha de A e cada linha de B como entidades únicas e retorna um vetor contendo 1 (verdadeiro), onde as linhas da matriz A também são linhas de B. Em outro lugar, ele retorna 0 (falso).
5	issorted(A) Retorna 1 lógico (verdadeiro) se os elementos de A estão em ordem de classificação e 0 lógico (falso) caso contrário. A entrada A pode ser um vetor ou uma matriz de sequências de células N por 1 ou 1 por N.A is considered to be sorted if A e a saída de sort (A) são iguais.
6	issorted(A, 'rows') Retorna 1 lógico (verdadeiro) se as linhas da matriz bidimensional A estão em ordem de classificação e 0 lógico (falso) caso contrário. Matrix A is considered to be sorted if A e a saída de sortrows (A) são iguais.
7	setdiff(A,B) Define a diferença de dois arrays; retorna os valores em A que não estão em B. Os valores na matriz retornada estão em ordem de classificação.
8	setdiff(A,B,'rows') Trata cada linha de A e cada linha de B como entidades únicas e retorna as linhas de A que não estão em B. As linhas da matriz retornada estão em ordem de classificação. A opção 'linhas' não oferece suporte a matrizes de células.
9	setxor Define OR exclusivo de duas matrizes
10	union Define a união de duas matrizes
11	unique Valores únicos na matriz

As estruturas de tomada de decisão requerem que o programador especifique uma ou mais condições a serem avaliadas ou testadas pelo programa, junto com uma instrução ou instruções a serem executadas se a condição for determinada como verdadeira e, opcionalmente, outras instruções a serem executadas se condição é determinada como falsa.

A seguir está a forma geral de uma estrutura típica de tomada de decisão encontrada na maioria das linguagens de programação -

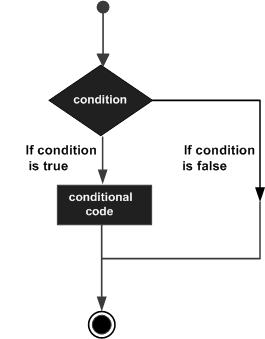
O MATLAB fornece os seguintes tipos de declarações de tomada de decisão. Clique nos links a seguir para verificar seus detalhes -

Sr. Não.	Declaração e descrição
1	if ... end statement A if ... end statement consiste em uma expressão booleana seguida por uma ou mais instruções.
2	if ... else ... end statement A if statement pode ser seguido por um opcional else statement, que é executado quando a expressão booleana é falsa.
3	If ... elseif ... elseif ... else ... instruções finais A if declaração pode ser seguida por um (ou mais) opcional elseif... e um else declaração, que é muito útil para testar várias condições.
4	declarações if aninhadas Você pode usar um if ou elseif declaração dentro de outra if ou elseif afirmações).
5	declaração switch UMA switch instrução permite que uma variável seja testada quanto à igualdade em relação a uma lista de valores.
6	instruções switch aninhadas Você pode usar um switch declaração dentro de outra switch afirmações).

Pode haver uma situação em que você precise executar um bloco de código várias vezes. Em geral, as instruções são executadas sequencialmente. A primeira instrução em uma função é executada primeiro, seguida pela segunda e assim por diante.

As linguagens de programação fornecem várias estruturas de controle que permitem caminhos de execução mais complicados.

Uma instrução de loop nos permite executar uma instrução ou grupo de instruções várias vezes e a seguir está a forma geral de uma instrução de loop na maioria das linguagens de programação -

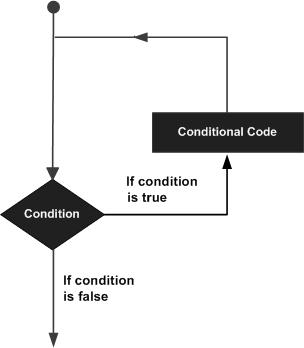
O MATLAB fornece os seguintes tipos de loops para lidar com os requisitos de loop. Clique nos links a seguir para verificar seus detalhes -

Sr. Não.	Tipo de Loop e Descrição
1	loop while Repete uma declaração ou grupo de declarações enquanto uma determinada condição for verdadeira. Ele testa a condição antes de executar o corpo do loop.
2	para loop Executa uma sequência de instruções várias vezes e abrevia o código que gerencia a variável de loop.
3	loops aninhados Você pode usar um ou mais loops dentro de qualquer outro loop.

Declarações de controle de loop

As instruções de controle de loop alteram a execução de sua sequência normal. Quando a execução deixa um escopo, todos os objetos automáticos que foram criados nesse escopo são destruídos.

O MATLAB suporta as seguintes instruções de controle. Clique nos links a seguir para verificar seus detalhes.

Sr. Não.	Declaração de controle e descrição
1	declaração de quebra Termina o loop instrução e transfere a execução para a instrução imediatamente após o loop.
2	continuar declaração Faz com que o loop pule o restante de seu corpo e teste novamente sua condição imediatamente antes de reiterar.

Um vetor é uma matriz unidimensional de números. O MATLAB permite a criação de dois tipos de vetores -

Vetores de linha
Vetores coluna

Vetores de linha

Row vectors são criados colocando o conjunto de elementos entre colchetes, usando espaço ou vírgula para delimitar os elementos.

r = [7 8 9 10 11]

O MATLAB executará a instrução acima e retornará o seguinte resultado -

r =

   7    8    9   10   11

Vetores de coluna

Column vectors são criados colocando o conjunto de elementos entre colchetes, usando ponto e vírgula para delimitar os elementos.

c = [7;  8;  9;  10; 11]

O MATLAB executará a instrução acima e retornará o seguinte resultado -

Referenciando os Elementos de um Vetor

Você pode fazer referência a um ou mais elementos de um vetor de várias maneiras. O i ^ésimo componente de um vetor v é referido como v (i). Por exemplo -

v = [ 1; 2; 3; 4; 5; 6];	% creating a column vector of 6 elements
v(3)

O MATLAB executará a instrução acima e retornará o seguinte resultado -

ans =  3

Quando você faz referência a um vetor com dois pontos, como v (:), todos os componentes do vetor são listados.

v = [ 1; 2; 3; 4; 5; 6];	% creating a column vector of 6 elements
v(:)

O MATLAB executará a instrução acima e retornará o seguinte resultado -

O MATLAB permite que você selecione uma gama de elementos de um vetor.

Por exemplo, vamos criar um vetor de linha rv de 9 elementos, então faremos referência aos elementos 3 a 7 escrevendorv(3:7)e crie um novo vetor denominado sub_rv .

rv = [1 2 3 4 5 6 7 8 9];
sub_rv = rv(3:7)

O MATLAB executará a instrução acima e retornará o seguinte resultado -

sub_rv =

   3   4   5   6   7

Operações de vetor

Nesta seção, vamos discutir as seguintes operações vetoriais -

Adição e subtração de vetores
Multiplicação escalar de vetores
Transposição de um vetor
Incluindo Vetores
Magnitude de um vetor
Produto interno vetorial
Vetores com Elementos Uniformemente Espaçados

Uma matriz é uma matriz bidimensional de números.

No MATLAB, você cria uma matriz inserindo elementos em cada linha como vírgulas ou números delimitados por espaço e usando ponto-e-vírgula para marcar o final de cada linha.

Por exemplo, vamos criar uma matriz 4 por 5 a -

a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8]

O MATLAB executará a instrução acima e retornará o seguinte resultado -

a =
      1     2     3     4     5
      2     3     4     5     6
      3     4     5     6     7
      4     5     6     7     8

Referenciando os Elementos de uma Matriz

Para fazer referência a um elemento na ^enésima linha ^enésima coluna, de uma matriz mx , escrevemos -

mx(m, n);

Por exemplo, para se referir ao elemento na 2 ^ª linha e 5 ^ª coluna, da matriz de um , como criado na última seção, digite -

a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8];
a(2,5)

O MATLAB executará a instrução acima e retornará o seguinte resultado -

ans =  6

Para fazer referência a todos os elementos na m- ^ésima coluna, digitamos A (:, m).

Vamos criar um vetor coluna v, a partir dos elementos da ^4ª linha da matriz a -

a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8];
v = a(:,4)

O MATLAB executará a instrução acima e retornará o seguinte resultado -

Você também pode selecionar os elementos na m ^th a n ^th colunas, para este write nós -

a(:,m:n)

Vamos criar uma matriz menor tomando os elementos da segunda e terceira colunas -

a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8];
a(:, 2:3)

O MATLAB executará a instrução acima e retornará o seguinte resultado -

Da mesma forma, você pode criar uma submatriz tomando uma subparte de uma matriz.

a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8];
a(:, 2:3)

O MATLAB executará a instrução acima e retornará o seguinte resultado -

Da mesma forma, você pode criar uma submatriz tomando uma subparte de uma matriz.

Por exemplo, vamos criar uma submatriz sa tomando a subparte interna de a -

3     4     5     
4     5     6

Para fazer isso, escreva -

a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8];
sa = a(2:3,2:4)

O MATLAB executará a instrução acima e retornará o seguinte resultado -

sa =
      3     4     5
      4     5     6

Excluindo uma linha ou coluna em uma matriz

Você pode excluir uma linha ou coluna inteira de uma matriz atribuindo um conjunto vazio de colchetes [] a essa linha ou coluna. Basicamente, [] denota uma matriz vazia.

Por exemplo, vamos deletar a quarta linha de um -

a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8];
a( 4 , : ) = []

O MATLAB executará a instrução acima e retornará o seguinte resultado -

a =
      1     2     3     4     5
      2     3     4     5     6
      3     4     5     6     7

A seguir, vamos deletar a quinta coluna de um -

a = [ 1 2 3 4 5; 2 3 4 5 6; 3 4 5 6 7; 4 5 6 7 8];
a(: , 5)=[]

O MATLAB executará a instrução acima e retornará o seguinte resultado -

a =
      1     2     3     4
      2     3     4     5
      3     4     5     6
      4     5     6     7

Exemplo

Neste exemplo, vamos criar uma matriz 3 por 3 m, então copiaremos a segunda e a terceira linhas desta matriz duas vezes para criar uma matriz 4 por 3.

Crie um arquivo de script com o seguinte código -

a = [ 1 2 3 ; 4 5 6; 7 8 9];
new_mat = a([2,3,2,3],:)

Quando você executa o arquivo, ele exibe o seguinte resultado -

new_mat =
      4     5     6
      7     8     9
      4     5     6
      7     8     9

Operações Matrix

Nesta seção, vamos discutir as seguintes operações de matriz básicas e comumente usadas -

Adição e subtração de matrizes
Divisão de Matrizes
Operações escalares de matrizes
Transpor uma matriz
Matrizes de concatenação
Multiplicação da matriz
Determinante de uma Matriz
Inverso de uma Matriz

Todas as variáveis de todos os tipos de dados no MATLAB são matrizes multidimensionais. Um vetor é uma matriz unidimensional e uma matriz é uma matriz bidimensional.

Já discutimos vetores e matrizes. Neste capítulo, discutiremos matrizes multidimensionais. No entanto, antes disso, vamos discutir alguns tipos especiais de arrays.

Matrizes especiais em MATLAB

Nesta seção, discutiremos algumas funções que criam alguns arrays especiais. Para todas essas funções, um único argumento cria uma matriz quadrada, os argumentos duplos criam uma matriz retangular.

o zeros() função cria uma matriz de todos os zeros -

Por exemplo -

zeros(5)

O MATLAB executará a instrução acima e retornará o seguinte resultado -

ans =
      0     0     0     0     0
      0     0     0     0     0
      0     0     0     0     0
      0     0     0     0     0
      0     0     0     0     0

o ones() função cria uma matriz de todos -

Por exemplo -

ones(4,3)

O MATLAB executará a instrução acima e retornará o seguinte resultado -

ans =
      1     1     1
      1     1     1
      1     1     1
      1     1     1

o eye() função cria uma matriz de identidade.

Por exemplo -

eye(4)

O MATLAB executará a instrução acima e retornará o seguinte resultado -

ans =
      1     0     0     0
      0     1     0     0
      0     0     1     0
      0     0     0     1

o rand() função cria uma matriz de números aleatórios uniformemente distribuídos em (0,1) -

Por exemplo -

rand(3, 5)

O MATLAB executará a instrução acima e retornará o seguinte resultado -

ans =
   0.8147    0.9134    0.2785    0.9649    0.9572
   0.9058    0.6324    0.5469    0.1576    0.4854
   0.1270    0.0975    0.9575    0.9706    0.8003

Um quadrado mágico

UMA magic square é um quadrado que produz a mesma soma, quando seus elementos são somados em linha, coluna ou diagonalmente.

o magic()função cria uma matriz quadrada mágica. É necessário um argumento singular que fornece o tamanho do quadrado. O argumento deve ser um escalar maior ou igual a 3.

magic(4)

O MATLAB executará a instrução acima e retornará o seguinte resultado -

ans =
   16     2     3    13
   5    11    10     8
   9     7     6    12
   4    14    15     1

Matrizes multidimensionais

Uma matriz com mais de duas dimensões é chamada de matriz multidimensional no MATLAB. Matrizes multidimensionais no MATLAB são uma extensão da matriz bidimensional normal.

Geralmente, para gerar uma matriz multidimensional, primeiro criamos uma matriz bidimensional e a estendemos.

Por exemplo, vamos criar um array bidimensional a.

a = [7 9 5; 6 1 9; 4 3 2]

O MATLAB executará a instrução acima e retornará o seguinte resultado -

a =
   7     9     5
   6     1     9
   4     3     2

A matriz a é uma matriz de 3 por 3; podemos adicionar uma terceira dimensão a a , fornecendo valores como -

a(:, :, 2)= [ 1 2 3; 4 5 6; 7 8 9]

O MATLAB executará a instrução acima e retornará o seguinte resultado -

a =

ans(:,:,1) =

   0   0   0
   0   0   0
   0   0   0

ans(:,:,2) =

   1   2   3
   4   5   6
   7   8   9

Também podemos criar arrays multidimensionais usando as funções uns (), zeros () ou rand ().

Por exemplo,

b = rand(4,3,2)

O MATLAB executará a instrução acima e retornará o seguinte resultado -

b(:,:,1) =
   0.0344    0.7952    0.6463
   0.4387    0.1869    0.7094
   0.3816    0.4898    0.7547
   0.7655    0.4456    0.2760

b(:,:,2) =
   0.6797    0.4984    0.2238
   0.6551    0.9597    0.7513
   0.1626    0.3404    0.2551
   0.1190    0.5853    0.5060

Também podemos usar o cat()função para construir arrays multidimensionais. Ele concatena uma lista de matrizes ao longo de uma dimensão especificada -

A sintaxe para a função cat () é -

B = cat(dim, A1, A2...)

Onde,

B é a nova matriz criada
A1 , A2 , ... são as matrizes a serem concatenadas
dim é a dimensão ao longo da qual concatenar as matrizes

Exemplo

Crie um arquivo de script e digite o seguinte código nele -

a = [9 8 7; 6 5 4; 3 2 1];
b = [1 2 3; 4 5 6; 7 8 9];
c = cat(3, a, b, [ 2 3 1; 4 7 8; 3 9 0])

Quando você executa o arquivo, ele exibe -

c(:,:,1) =
      9     8     7
      6     5     4
      3     2     1
c(:,:,2) =
      1     2     3
      4     5     6
      7     8     9
c(:,:,3) =
      2     3     1
      4     7     8
      3     9     0

Funções de matriz

O MATLAB fornece as seguintes funções para classificar, girar, permutar, remodelar ou mudar o conteúdo da matriz.

Função	Objetivo
comprimento	Comprimento do vetor ou maior dimensão da matriz
ndims	Número de dimensões da matriz
numel	Número de elementos da matriz
Tamanho	Dimensões da matriz
iscolumn	Determina se a entrada é um vetor de coluna
está vazia	Determina se a matriz está vazia
ismatriz	Determina se a entrada é uma matriz
Isrow	Determina se a entrada é um vetor linha
isscalar	Determina se a entrada é escalar
isvetor	Determina se a entrada é um vetor
blkdiag	Constrói matriz diagonal de bloco a partir de argumentos de entrada
circshift	Muda a matriz circularmente
transpor	Transposição de conjugado complexo
diag	Matrizes diagonais e diagonais da matriz
flipdim	Inverte a matriz ao longo da dimensão especificada
fliplr	Inverte a matriz da esquerda para a direita
flipud	Inverte a matriz de cima para baixo
ipermute	Inversa dimensões de permuta de matriz ND
permutar	Reorganiza as dimensões da matriz ND
repmat	Replicações e matriz de blocos
remodelar	Remodela a matriz
rot90	Roda a matriz 90 graus
shiftdim	Dimensões de deslocamento
ordenado	Determina se os elementos do conjunto estão em ordem de classificação
ordenar	Classifica os elementos da matriz em ordem crescente ou decrescente
sortrows	Classifica as linhas em ordem crescente
aperto	Remove dimensões singleton
transpor	Transpor
vetorizar	Vectoriza a expressão

Exemplos

Os exemplos a seguir ilustram algumas das funções mencionadas acima.

Length, Dimension and Number of elements −

Crie um arquivo de script e digite o seguinte código nele -

x = [7.1, 3.4, 7.2, 28/4, 3.6, 17, 9.4, 8.9];
length(x)      % length of x vector
y = rand(3, 4, 5, 2);
ndims(y)       % no of dimensions in array y
s = ['Zara', 'Nuha', 'Shamim', 'Riz', 'Shadab'];
numel(s)       % no of elements in s

Quando você executa o arquivo, ele exibe o seguinte resultado -

ans =  8
ans =  4
ans =  23

Circular Shifting of the Array Elements −

Crie um arquivo de script e digite o seguinte código nele -

a = [1 2 3; 4 5 6; 7 8 9]  % the original array a
b = circshift(a,1)         %  circular shift first dimension values down by 1.
c = circshift(a,[1 -1])    % circular shift first dimension values % down by 1 
                           % and second dimension values to the left % by 1.

Quando você executa o arquivo, ele exibe o seguinte resultado -

a =
   1     2     3
   4     5     6
   7     8     9

b =
   7     8     9
   1     2     3
   4     5     6

c =
   8     9     7
   2     3     1
   5     6     4

Classificando matrizes

Crie um arquivo de script e digite o seguinte código nele -

v = [ 23 45 12 9 5 0 19 17]  % horizontal vector
sort(v)                      % sorting v
m = [2 6 4; 5 3 9; 2 0 1]    % two dimensional array
sort(m, 1)                   % sorting m along the row
sort(m, 2)                   % sorting m along the column

Quando você executa o arquivo, ele exibe o seguinte resultado -

v =
   23    45    12     9     5     0    19    17
ans =
   0     5     9    12    17    19    23    45
m =
   2     6     4
   5     3     9
   2     0     1
ans =
   2     0     1
   2     3     4
   5     6     9
ans =
   2     4     6
   3     5     9
   0     1     2

Matriz de Células

Matrizes de células são matrizes de células indexadas em que cada célula pode armazenar uma matriz de dimensões e tipos de dados diferentes.

o cellfunção é usada para criar uma matriz de células. A sintaxe para a função da célula é -

C = cell(dim)
C = cell(dim1,...,dimN)
D = cell(obj)

Onde,

C é a matriz de células;
dim é um inteiro escalar ou vetor de inteiros que especifica as dimensões da matriz de células C;
dim1, ..., dimN são inteiros escalares que especificam as dimensões de C;
obj é um dos seguintes -
- Array ou objeto Java
- Matriz .NET do tipo System.String ou System.Object

Exemplo

Crie um arquivo de script e digite o seguinte código nele -

c = cell(2, 5);
c = {'Red', 'Blue', 'Green', 'Yellow', 'White'; 1 2 3 4 5}

Quando você executa o arquivo, ele exibe o seguinte resultado -

c = 
{
   [1,1] = Red
   [2,1] =  1
   [1,2] = Blue
   [2,2] =  2
   [1,3] = Green
   [2,3] =  3
   [1,4] = Yellow
   [2,4] =  4
   [1,5] = White
   [2,5] =  5
}

Acessando dados em matrizes de células

Existem duas maneiras de se referir aos elementos de uma matriz de células -

Fechando os índices no primeiro colchete (), para se referir a conjuntos de células
Colocando os índices entre colchetes {}, para se referir aos dados dentro das células individuais

Quando você coloca os índices no primeiro colchete, eles se referem ao conjunto de células.

Os índices de matriz de células entre parênteses suaves referem-se a conjuntos de células.

Por exemplo -

c = {'Red', 'Blue', 'Green', 'Yellow', 'White'; 1 2 3 4 5};
c(1:2,1:2)

O MATLAB executará a instrução acima e retornará o seguinte resultado -

ans = 
{
   [1,1] = Red
   [2,1] =  1
   [1,2] = Blue
   [2,2] =  2
}

Você também pode acessar o conteúdo das células indexando com chaves.

Por exemplo -

c = {'Red', 'Blue', 'Green', 'Yellow', 'White'; 1 2 3 4 5};
c{1, 2:4}

O MATLAB executará a instrução acima e retornará o seguinte resultado -

ans = Blue
ans = Green
ans = Yellow

o colon(:)é um dos operadores mais úteis do MATLAB. É usado para criar vetores, matrizes de subscrito especify for iterations.

Se você deseja criar um vetor linha, contendo inteiros de 1 a 10, você escreve -

1:10

O MATLAB executa a instrução e retorna um vetor linha contendo os inteiros de 1 a 10 -

ans =                                                                           
                                                                                
   1    2    3    4    5    6    7    8    9   10

Se você deseja especificar um valor de incremento diferente de um, por exemplo -

100: -5: 50

O MATLAB executa a instrução e retorna o seguinte resultado -

ans =
   100    95    90    85    80    75    70    65    60    55    50

Vejamos outro exemplo -

0:pi/8:pi

O MATLAB executa a instrução e retorna o seguinte resultado -

ans =
   Columns 1 through 7
      0    0.3927    0.7854    1.1781    1.5708    1.9635    2.3562
   Columns 8 through 9
      2.7489    3.1416

Você pode usar o operador de dois pontos para criar um vetor de índices para selecionar linhas, colunas ou elementos de matrizes.

A tabela a seguir descreve seu uso para este propósito (vamos ter uma matriz A) -

Formato	Objetivo
A(:,j)	é a jª coluna de A.
A(i,:)	é a iésima linha de A.
A(:,:)	é a matriz bidimensional equivalente. Para matrizes, é igual a A.
A(j:k)	é A (j), A (j + 1), ..., A (k).
A(:,j:k)	é A (:, j), A (:, j + 1), ..., A (:, k).
A(:,:,k)	é a k ^ésima página da matriz tridimensional A.
A(i,j,k,:)	é um vetor em uma matriz quadridimensional A. O vetor inclui A (i, j, k, 1), A (i, j, k, 2), A (i, j, k, 3) e assim por diante.
A(:)	são todos os elementos de A, considerados como uma única coluna. No lado esquerdo de uma instrução de atribuição, A (:) preenche A, preservando sua forma anterior. Nesse caso, o lado direito deve conter o mesmo número de elementos que A.

Exemplo

Crie um arquivo de script e digite o seguinte código nele -

A = [1 2 3 4; 4 5 6 7; 7 8 9 10]
A(:,2)      % second column of A
A(:,2:3)    % second and third column of A
A(2:3,2:3)  % second and third rows and second and third columns

Quando você executa o arquivo, ele exibe o seguinte resultado -

A =
      1     2     3     4
      4     5     6     7
      7     8     9    10

ans =
      2
      5
      8

ans =
      2     3
      5     6
      8     9

ans =
      5     6
      8     9

O MATLAB suporta várias classes numéricas que incluem inteiros com sinal e sem sinal e números de ponto flutuante de precisão simples e dupla. Por padrão, o MATLAB armazena todos os valores numéricos como números de ponto flutuante de precisão dupla.

Você pode escolher armazenar qualquer número ou matriz de números como inteiros ou como números de precisão simples.

Todos os tipos numéricos suportam operações básicas de array e operações matemáticas.

Conversão para vários tipos de dados numéricos

O MATLAB fornece as seguintes funções para converter em vários tipos de dados numéricos -

Função	Objetivo
em dobro	Converte em número de precisão dupla
solteiro	Converte em número de precisão simples
int8	Converte em inteiro assinado de 8 bits
int16	Converte em inteiro assinado de 16 bits
int32	Converte em inteiro assinado de 32 bits
int64	Converte em inteiro assinado de 64 bits
uint8	Converte em inteiro sem sinal de 8 bits
uint16	Converte em inteiro não assinado de 16 bits
uint32	Converte em inteiro sem sinal de 32 bits
uint64	Converte em inteiro sem sinal de 64 bits

Exemplo

Crie um arquivo de script e digite o seguinte código -

x = single([5.32 3.47 6.28]) .* 7.5
x = double([5.32 3.47 6.28]) .* 7.5
x = int8([5.32 3.47 6.28]) .* 7.5
x = int16([5.32 3.47 6.28]) .* 7.5
x = int32([5.32 3.47 6.28]) .* 7.5
x = int64([5.32 3.47 6.28]) .* 7.5

Quando você executa o arquivo, ele mostra o seguinte resultado -

x =

   39.900   26.025   47.100

x =

   39.900   26.025   47.100

x =

   38  23  45

x =

   38  23  45

x =

   38  23  45

x =

   38  23  45

Exemplo

Vamos estender o exemplo anterior um pouco mais. Crie um arquivo de script e digite o seguinte código -

x = int32([5.32 3.47 6.28]) .* 7.5
x = int64([5.32 3.47 6.28]) .* 7.5
x = num2cell(x)

Quando você executa o arquivo, ele mostra o seguinte resultado -

x =

   38  23  45

x =

   38  23  45

x = 
{
   [1,1] = 38
   [1,2] = 23
   [1,3] = 45
}

Inteiros menores e maiores

As funções intmax() e intmin() retorna os valores máximo e mínimo que podem ser representados com todos os tipos de números inteiros.

Ambas as funções usam o tipo de dados inteiro como argumento, por exemplo, intmax (int8) ou intmin (int64) e retornam os valores máximo e mínimo que você pode representar com o tipo de dados inteiro.

Exemplo

O exemplo a seguir ilustra como obter o menor e o maior valor de inteiros. Crie um arquivo de script e escreva o seguinte código nele -

% displaying the smallest and largest signed integer data
str = 'The range for int8 is:\n\t%d to %d ';
sprintf(str, intmin('int8'), intmax('int8'))
str = 'The range for int16 is:\n\t%d to %d ';
sprintf(str, intmin('int16'), intmax('int16'))
str = 'The range for int32 is:\n\t%d to %d ';
sprintf(str, intmin('int32'), intmax('int32'))
str = 'The range for int64 is:\n\t%d to %d ';
sprintf(str, intmin('int64'), intmax('int64'))
 
% displaying the smallest and largest unsigned integer data
str = 'The range for uint8 is:\n\t%d to %d ';
sprintf(str, intmin('uint8'), intmax('uint8'))
str = 'The range for uint16 is:\n\t%d to %d ';
sprintf(str, intmin('uint16'), intmax('uint16'))
str = 'The range for uint32 is:\n\t%d to %d ';
sprintf(str, intmin('uint32'), intmax('uint32'))
str = 'The range for uint64 is:\n\t%d to %d ';
sprintf(str, intmin('uint64'), intmax('uint64'))

Quando você executa o arquivo, ele mostra o seguinte resultado -

ans = The range for int8 is:
	-128 to 127 
ans = The range for int16 is:
	-32768 to 32767 
ans = The range for int32 is:
	-2147483648 to 2147483647 
ans = The range for int64 is:
	0 to 0 
ans = The range for uint8 is:
	0 to 255 
ans = The range for uint16 is:
	0 to 65535 
ans = The range for uint32 is:
	0 to -1 
ans = The range for uint64 is:
	0 to 18446744073709551616

Números de ponto flutuante menores e maiores

As funções realmax() e realmin() retorna os valores máximo e mínimo que podem ser representados com números de ponto flutuante.

Ambas as funções, quando chamadas com o argumento 'único', retornam os valores máximo e mínimo que você pode representar com o tipo de dados de precisão simples e quando chamadas com o argumento 'duplo', retornam os valores máximo e mínimo que você pode representar com o tipo de dados de precisão dupla.

Exemplo

O exemplo a seguir ilustra como obter os menores e maiores números de ponto flutuante. Crie um arquivo de script e escreva o seguinte código nele -

% displaying the smallest and largest single-precision 
% floating point number
str = 'The range for single is:\n\t%g to %g and\n\t %g to  %g';
sprintf(str, -realmax('single'), -realmin('single'), ...
   realmin('single'), realmax('single'))

% displaying the smallest and largest double-precision 
% floating point number
str = 'The range for double is:\n\t%g to %g and\n\t %g to  %g';
sprintf(str, -realmax('double'), -realmin('double'), ...
   realmin('double'), realmax('double'))

Quando você executa o arquivo, ele exibe o seguinte resultado -

ans = The range for single is:                                                  
        -3.40282e+38 to -1.17549e-38 and                                        
         1.17549e-38 to  3.40282e+38                                            
ans = The range for double is:                                                  
        -1.79769e+308 to -2.22507e-308 and                                      
         2.22507e-308 to  1.79769e+308

Criar uma string de caracteres é bastante simples no MATLAB. Na verdade, já o usamos muitas vezes. Por exemplo, você digita o seguinte no prompt de comando -

my_string = 'Tutorials Point'

O MATLAB executará a instrução acima e retornará o seguinte resultado -

my_string = Tutorials Point

O MATLAB considera todas as variáveis como arrays e as strings são consideradas arrays de caracteres. Vamos usar owhos comando para verificar a variável criada acima -

whos

O MATLAB executará a instrução acima e retornará o seguinte resultado -

Name           Size            Bytes  Class    Attributes
my_string      1x16               32  char

Curiosamente, você pode usar funções de conversão numérica como uint8 ou uint16para converter os caracteres da string em seus códigos numéricos. ochar função converte o vetor inteiro de volta em caracteres -

Exemplo

Crie um arquivo de script e digite o seguinte código nele -

my_string = 'Tutorial''s Point';
str_ascii = uint8(my_string)        % 8-bit ascii values
str_back_to_char= char(str_ascii)  
str_16bit = uint16(my_string)       % 16-bit ascii values
str_back_to_char = char(str_16bit)

Quando você executa o arquivo, ele exibe o seguinte resultado -

str_ascii =

   84  117  116  111  114  105   97  108   39  115   32   80  111  105  110  116

str_back_to_char = Tutorial's Point
str_16bit =

   84  117  116  111  114  105   97  108   39  115   32   80  111  105  110  116

str_back_to_char = Tutorial's Point

Matriz Retangular de Caracteres

As strings que discutimos até agora são matrizes de caracteres unidimensionais; no entanto, precisamos armazenar mais do que isso. Precisamos armazenar mais dados textuais dimensionais em nosso programa. Isso é obtido através da criação de matrizes de caracteres retangulares.

A maneira mais simples de criar uma matriz de caracteres retangular é concatenando duas ou mais matrizes de caracteres unidimensionais, vertical ou horizontalmente, conforme necessário.

Você pode combinar strings verticalmente de uma das seguintes maneiras -

Usando o operador de concatenação MATLAB []e separando cada linha com um ponto e vírgula (;). Observe que neste método cada linha deve conter o mesmo número de caracteres. Para strings com comprimentos diferentes, você deve preencher com caracteres de espaço conforme necessário.
Usando o charfunção. Se as strings forem de comprimentos diferentes, char preenche as strings mais curtas com espaços em branco à direita para que cada linha tenha o mesmo número de caracteres.

Exemplo

Crie um arquivo de script e digite o seguinte código nele -

doc_profile = ['Zara Ali                             '; ...
               'Sr. Surgeon                          '; ...
               'R N Tagore Cardiology Research Center']
doc_profile = char('Zara Ali', 'Sr. Surgeon', ...
                  'RN Tagore Cardiology Research Center')

Quando você executa o arquivo, ele exibe o seguinte resultado -

doc_profile =
Zara Ali                             
Sr. Surgeon                          
R N Tagore Cardiology Research Center
doc_profile =
Zara Ali                            
Sr. Surgeon                         
RN Tagore Cardiology Research Center

Você pode combinar strings horizontalmente de uma das seguintes maneiras -

Usando o operador de concatenação MATLAB, []e separar as strings de entrada com uma vírgula ou um espaço. Este método preserva todos os espaços finais nas matrizes de entrada.
Usando a função de concatenação de string, strcat. Este método remove espaços à direita nas entradas.

Exemplo

Crie um arquivo de script e digite o seguinte código nele -

name =     'Zara Ali                             ';
position = 'Sr. Surgeon                          '; 
worksAt =  'R N Tagore Cardiology Research Center';
profile = [name ', ' position ', ' worksAt]
profile = strcat(name, ', ', position, ', ', worksAt)

Quando você executa o arquivo, ele exibe o seguinte resultado -

profile = Zara Ali      , Sr. Surgeon      , R N Tagore Cardiology Research Center
profile = Zara Ali,Sr. Surgeon,R N Tagore Cardiology Research Center

Combinando Strings em uma Matriz Celular

De nossa discussão anterior, está claro que combinar strings com comprimentos diferentes pode ser uma dor, já que todas as strings no array têm que ter o mesmo comprimento. Usamos espaços em branco no final das strings para equalizar seu comprimento.

No entanto, uma maneira mais eficiente de combinar as strings é converter a matriz resultante em uma matriz de células.

A matriz de células do MATLAB pode conter diferentes tamanhos e tipos de dados em uma matriz. Matrizes de células fornecem uma maneira mais flexível de armazenar strings de comprimento variável.

o cellstr função converte uma matriz de caracteres em uma matriz de células de strings.

Exemplo

Crie um arquivo de script e digite o seguinte código nele -

name =     'Zara Ali                             ';
position = 'Sr. Surgeon                          '; 
worksAt =  'R N Tagore Cardiology Research Center';
profile = char(name, position, worksAt);
profile = cellstr(profile);
disp(profile)

Quando você executa o arquivo, ele exibe o seguinte resultado -

{                                                                               
   [1,1] = Zara Ali                                                              
   [2,1] = Sr. Surgeon                                                           
   [3,1] = R N Tagore Cardiology Research Center                                 
}

Funções de string no MATLAB

O MATLAB fornece várias funções de string criando, combinando, analisando, comparando e manipulando strings.

A tabela a seguir fornece uma breve descrição das funções de string no MATLAB -

Função	Objetivo
Funções para armazenar texto em matrizes de caracteres, combinar matrizes de caracteres, etc.
espaços em branco	Crie uma sequência de caracteres em branco
cellstr	Crie uma matriz de células de strings a partir da matriz de caracteres
Caracteres	Converter para matriz de caracteres (string)
iscellstr	Determine se a entrada é uma matriz de células de strings
ischar	Determine se o item é uma matriz de caracteres
sprintf	Formatar dados em string
strcat	Concatenar strings horizontalmente
strjoin	Junte strings na matriz de células em uma única string
Funções para identificar partes de strings, localizar e substituir substrings
ischar	Determine se o item é uma matriz de caracteres
isletter	Elementos da matriz que são letras alfabéticas
isspace	Elementos de matriz que são caracteres de espaço
isstrprop	Determine se a string pertence à categoria especificada
sscanf	Leia os dados formatados da string
strfind	Encontre uma string dentro de outra
strrep	Encontrar e substituir substring
strsplit	Dividir string no delimitador especificado
Strtok	Partes selecionadas da corda
validatestring	Verifique a validade da string de texto
Symvar	Determine variáveis simbólicas na expressão
regexp	Corresponder à expressão regular (diferencia maiúsculas de minúsculas)
regexpi	Corresponder à expressão regular (não diferencia maiúsculas de minúsculas)
regexprep	Substitua a string usando uma expressão regular
regexptranslate	Traduzir string em expressão regular
Funções para comparação de strings
strcmp	Compare strings (diferencia maiúsculas de minúsculas)
strcmpi	Compare strings (não diferencia maiúsculas de minúsculas)
strncmp	Compare os primeiros n caracteres de strings (diferencia maiúsculas de minúsculas)
strncmpi	Compare os primeiros n caracteres de strings (não diferencia maiúsculas de minúsculas)
Funções para alterar a string para maiúsculas ou minúsculas, criando ou removendo espaços em branco
esvaziar	Retire os espaços em branco à direita do final da string
strtrim	Remova o espaço em branco à esquerda e à direita da string
mais baixo	Converter string em minúsculas
superior	Converter string em maiúsculas
strjust	Justificar matriz de caracteres

Exemplos

Os exemplos a seguir ilustram algumas das funções de string mencionadas acima -

Formatando Strings

Crie um arquivo de script e digite o seguinte código nele -

A = pi*1000*ones(1,5);
sprintf(' %f \n %.2f \n %+.2f \n %12.2f \n %012.2f \n', A)

Quando você executa o arquivo, ele exibe o seguinte resultado -

ans =  3141.592654 
   3141.59 
   +3141.59 
      3141.59 
   000003141.59

Unindo Strings

Crie um arquivo de script e digite o seguinte código nele -

%cell array of strings
str_array = {'red','blue','green', 'yellow', 'orange'};

% Join strings in cell array into single string
str1 = strjoin(str_array, "-")
str2 = strjoin(str_array, ",")

Quando você executa o arquivo, ele exibe o seguinte resultado -

str1 = red-blue-green-yellow-orange
str2 = red,blue,green,yellow,orange

Localizando e Substituindo Strings

Crie um arquivo de script e digite o seguinte código nele -

students = {'Zara Ali', 'Neha Bhatnagar', ...
            'Monica Malik', 'Madhu Gautam', ...
            'Madhu Sharma', 'Bhawna Sharma',...
            'Nuha Ali', 'Reva Dutta', ...
            'Sunaina Ali', 'Sofia Kabir'};
 
% The strrep function searches and replaces sub-string.
new_student = strrep(students(8), 'Reva', 'Poulomi')
% Display first names
first_names = strtok(students)

Quando você executa o arquivo, ele exibe o seguinte resultado -

new_student = 
{
   [1,1] = Poulomi Dutta
}
first_names = 
{
   [1,1] = Zara
   [1,2] = Neha
   [1,3] = Monica
   [1,4] = Madhu
   [1,5] = Madhu
   [1,6] = Bhawna
   [1,7] = Nuha
   [1,8] = Reva
   [1,9] = Sunaina
   [1,10] = Sofia
}

Comparando Strings

Crie um arquivo de script e digite o seguinte código nele -

str1 = 'This is test'
str2 = 'This is text'
if (strcmp(str1, str2))
   sprintf('%s and %s are equal', str1, str2)
else
   sprintf('%s and %s are not equal', str1, str2)
end

Quando você executa o arquivo, ele exibe o seguinte resultado -

str1 = This is test
str2 = This is text
ans = This is test and This is text are not equal

Uma função é um grupo de instruções que, juntas, executam uma tarefa. No MATLAB, as funções são definidas em arquivos separados. O nome do arquivo e da função deve ser o mesmo.

As funções operam em variáveis dentro de seu próprio espaço de trabalho, que também é chamado de local workspace, separado do espaço de trabalho que você acessa no prompt de comando do MATLAB, que é chamado de base workspace.

As funções podem aceitar mais de um argumento de entrada e podem retornar mais de um argumento de saída.

A sintaxe de uma declaração de função é -

function [out1,out2, ..., outN] = myfun(in1,in2,in3, ..., inN)

Exemplo

A seguinte função chamada mymax deve ser escrita em um arquivo chamado mymax.m . Leva cinco números como argumento e retorna o máximo dos números.

Crie um arquivo de função, denominado mymax.m, e digite o seguinte código nele -

function max = mymax(n1, n2, n3, n4, n5)

%This function calculates the maximum of the
% five numbers given as input
max =  n1;
if(n2 > max)
   max = n2;
end
if(n3 > max)
   max = n3;
end
if(n4 > max)
   max = n4;
end
if(n5 > max)
   max = n5;
end

A primeira linha de uma função começa com a palavra-chave function. Fornece o nome da função e a ordem dos argumentos. Em nosso exemplo, a função mymax tem cinco argumentos de entrada e um argumento de saída.

As linhas de comentário que vêm logo após a instrução da função fornecem o texto de ajuda. Essas linhas são impressas quando você digita -

help mymax

O MATLAB executará a instrução acima e retornará o seguinte resultado -

This function calculates the maximum of the
   five numbers given as input

Você pode chamar a função como -

mymax(34, 78, 89, 23, 11)

O MATLAB executará a instrução acima e retornará o seguinte resultado -

ans = 89

Funções anônimas

Uma função anônima é como uma função embutida em linguagens de programação tradicionais, definida em uma única instrução MATLAB. Consiste em uma única expressão MATLAB e qualquer número de argumentos de entrada e saída.

Você pode definir uma função anônima diretamente na linha de comando do MATLAB ou em uma função ou script.

Desta forma, você pode criar funções simples sem ter que criar um arquivo para elas.

A sintaxe para criar uma função anônima a partir de uma expressão é

f = @(arglist)expression

Exemplo

Neste exemplo, escreveremos uma função anônima chamada potência, que receberá dois números como entrada e retornará o primeiro número elevado à potência do segundo número.

Crie um arquivo de script e digite o seguinte código nele -

power = @(x, n) x.^n;
result1 = power(7, 3)
result2 = power(49, 0.5)
result3 = power(10, -10)
result4 = power (4.5, 1.5)

Quando você executa o arquivo, ele exibe -

result1 =  343
result2 =  7
result3 =  1.0000e-10
result4 =  9.5459

Primária e Subfunções

Qualquer função diferente de uma função anônima deve ser definida em um arquivo. Cada arquivo de função contém uma função primária necessária que aparece primeiro e qualquer número de subfunções opcionais que vêm depois da função primária e são usadas por ela.

As funções primárias podem ser chamadas de fora do arquivo que as define, seja da linha de comando ou de outras funções, mas as subfunções não podem ser chamadas da linha de comando ou de outras funções, fora do arquivo de função.

As subfunções são visíveis apenas para a função primária e outras subfunções dentro do arquivo de função que as define.

Exemplo

Vamos escrever uma função chamada quadrática que calcularia as raízes de uma equação quadrática. A função teria três entradas, o coeficiente quadrático, o coeficiente linear e o termo constante. Ele devolveria as raízes.

O arquivo de função quadratic.m conterá a função primária quadrática e o disco de subfunção , que calcula o discriminante.

Crie um arquivo de função quadratic.m e digite o seguinte código nele -

function [x1,x2] = quadratic(a,b,c)

%this function returns the roots of 
% a quadratic equation.
% It takes 3 input arguments
% which are the co-efficients of x2, x and the 
%constant term
% It returns the roots
d = disc(a,b,c); 
x1 = (-b + d) / (2*a);
x2 = (-b - d) / (2*a);
end   % end of quadratic

function dis = disc(a,b,c) 
%function calculates the discriminant
dis = sqrt(b^2 - 4*a*c);
end   % end of sub-function

Você pode chamar a função acima no prompt de comando como -

quadratic(2,4,-4)

O MATLAB executará a instrução acima e retornará o seguinte resultado -

ans = 0.7321

Funções Aninhadas

Você pode definir funções dentro do corpo de outra função. Elas são chamadas de funções aninhadas. Uma função aninhada contém qualquer um ou todos os componentes de qualquer outra função.

As funções aninhadas são definidas dentro do escopo de outra função e compartilham o acesso ao espaço de trabalho da função contida.

Uma função aninhada segue a seguinte sintaxe -

function x = A(p1, p2)
...
B(p2)
   function y = B(p3)
   ...
   end
...
end

Exemplo

Vamos reescrever a função quadrática , do exemplo anterior, entretanto, desta vez a função de disco será uma função aninhada.

Crie um arquivo de função quadratic2.m e digite o seguinte código nele -

function [x1,x2] = quadratic2(a,b,c)
function disc  % nested function
d = sqrt(b^2 - 4*a*c);
end   % end of function disc

disc;
x1 = (-b + d) / (2*a);
x2 = (-b - d) / (2*a);
end   % end of function quadratic2

Você pode chamar a função acima no prompt de comando como -

quadratic2(2,4,-4)

O MATLAB executará a instrução acima e retornará o seguinte resultado -

ans =  0.73205

Funções Privadas

Uma função privada é uma função primária que é visível apenas para um grupo limitado de outras funções. Se você não quiser expor a implementação de uma (s) função (ões), pode criá-las como funções privadas.

As funções privadas residem em subfolders com o nome especial private.

Eles são visíveis apenas para funções na pasta pai.

Exemplo

Vamos reescrever a função quadrática . Desta vez, porém, a função de disco que calcula o discriminante será uma função privada.

Crie uma subpasta chamada private no diretório de trabalho. Armazene o seguinte arquivo de função disc.m nele -

function dis = disc(a,b,c) 
%function calculates the discriminant
dis = sqrt(b^2 - 4*a*c);
end      % end of sub-function

Crie uma função quadratic3.m em seu diretório de trabalho e digite o seguinte código nela -

function [x1,x2] = quadratic3(a,b,c)

%this function returns the roots of 
% a quadratic equation.
% It takes 3 input arguments
% which are the co-efficient of x2, x and the 
%constant term
% It returns the roots
d = disc(a,b,c); 

x1 = (-b + d) / (2*a);
x2 = (-b - d) / (2*a);
end      % end of quadratic3

Você pode chamar a função acima no prompt de comando como -

quadratic3(2,4,-4)

O MATLAB executará a instrução acima e retornará o seguinte resultado -

ans =  0.73205

Variáveis globais

Variáveis globais podem ser compartilhadas por mais de uma função. Para isso, você precisa declarar a variável como global em todas as funções.

Se você deseja acessar essa variável a partir do espaço de trabalho básico, declare a variável na linha de comando.

A declaração global deve ocorrer antes que a variável seja realmente usada em uma função. É uma boa prática usar letras maiúsculas nos nomes das variáveis globais para distingui-las de outras variáveis.

Exemplo

Vamos criar um arquivo de função denominado average.m e digitar o seguinte código nele -

function avg = average(nums)
global TOTAL
avg = sum(nums)/TOTAL;
end

Crie um arquivo de script e digite o seguinte código nele -

global TOTAL;
TOTAL = 10;
n = [34, 45, 25, 45, 33, 19, 40, 34, 38, 42];
av = average(n)

Quando você executa o arquivo, ele exibe o seguinte resultado -

av =  35.500

Importar dados no MATLAB significa carregar dados de um arquivo externo. oimportdatafunção permite carregar vários arquivos de dados de diferentes formatos. Possui os seguintes cinco formulários -

Sr. Não.	Descrição da função
1	A = importdata(filename) Carrega dados na matriz A do arquivo indicado por nome de arquivo .
2	A = importdata('-pastespecial') Carrega dados da área de transferência do sistema em vez de um arquivo.
3	A = importdata(___, delimiterIn) Interpreta delimiterIn como o separador de coluna no arquivo ASCII, nome do arquivo ou dados da área de transferência. Você pode usar delimiterIn com qualquer um dos argumentos de entrada nas sintaxes acima.
4	A = importdata(___, delimiterIn, headerlinesIn) Carrega dados de um arquivo ASCII, nome do arquivo ou área de transferência, lendo dados numéricos a partir de headerlinesIn + 1 .
5	[A, delimiterOut, headerlinesOut] = importdata(___) Retorna o caractere delimitador detectado para o arquivo ASCII de entrada em delimiterOut e o número detectado de linhas de cabeçalho em headerlinesOut , usando qualquer um dos argumentos de entrada nas sintaxes anteriores.

Por padrão, o Octave não tem suporte para a função importdata () , então você terá que pesquisar e instalar este pacote para que os exemplos a seguir funcionem com sua instalação do Octave.

Exemplo 1

Vamos carregar e exibir um arquivo de imagem. Crie um arquivo de script e digite o seguinte código nele -

filename = 'smile.jpg';
A = importdata(filename);
image(A);

Quando você executa o arquivo, o MATLAB exibe o arquivo de imagem. No entanto, você deve armazená-lo no diretório atual.

Exemplo 2

Neste exemplo, importamos um arquivo de texto e especificamos Delimitador e Cabeçalho da Coluna. Vamos criar um arquivo ASCII delimitado por espaço com cabeçalhos de coluna, chamado Weeklydata.txt .

Nosso arquivo de texto Weeklydata.txt se parece com isto -

SunDay  MonDay  TuesDay  WednesDay  ThursDay  FriDay  SaturDay
95.01   76.21   61.54    40.57       55.79    70.28   81.53
73.11   45.65   79.19    93.55       75.29    69.87   74.68
60.68   41.85   92.18    91.69       81.32    90.38   74.51
48.60   82.14   73.82    41.03       0.99     67.22   93.18
89.13   44.47   57.63    89.36       13.89    19.88   46.60

Crie um arquivo de script e digite o seguinte código nele -

filename = 'weeklydata.txt';
delimiterIn = ' ';
headerlinesIn = 1;
A = importdata(filename,delimiterIn,headerlinesIn);

% View data
for k = [1:7]
   disp(A.colheaders{1, k})
   disp(A.data(:, k))
   disp(' ')
end

Quando você executa o arquivo, ele exibe o seguinte resultado -

Exemplo 3

Neste exemplo, vamos importar dados da área de transferência.

Copie as seguintes linhas para a área de transferência -

Mathematics is simple

Crie um arquivo de script e digite o seguinte código -

A = importdata('-pastespecial')

Quando você executa o arquivo, ele exibe o seguinte resultado -

A = 
   'Mathematics is simple'

E / S de arquivo de baixo nível

A função importdata é uma função de alto nível. As funções de E / S de arquivo de baixo nível no MATLAB permitem o máximo controle sobre a leitura ou gravação de dados em um arquivo. No entanto, essas funções precisam de informações mais detalhadas sobre o arquivo para funcionar de maneira eficiente.

O MATLAB fornece as seguintes funções para operações de leitura e gravação no nível de byte ou caractere -

Função	Descrição
fclose	Feche um ou todos os arquivos abertos
feof	Teste de fim de arquivo
Ferror	Informações sobre erros de E / S de arquivo
fgetl	Leia a linha do arquivo, removendo caracteres de nova linha
fgets	Leia a linha do arquivo, mantendo os caracteres de nova linha
fopen	Abra o arquivo ou obtenha informações sobre os arquivos abertos
fprintf	Grave dados em arquivo de texto
fread	Leia os dados do arquivo binário
Frewind	Mova o indicador de posição do arquivo para o início do arquivo aberto
fscanf	Leia os dados do arquivo de texto
fseek	Mover para a posição especificada no arquivo
ftell	Posição no arquivo aberto
fwrite	Grave dados em arquivo binário

Importar arquivos de dados de texto com E / S de baixo nível

O MATLAB fornece as seguintes funções para importação de baixo nível de arquivos de dados de texto -

o fscanf função lê dados formatados em um texto ou arquivo ASCII.
o fgetl e fgets funções lêem uma linha de um arquivo por vez, onde um caractere de nova linha separa cada linha.
o fread função lê um fluxo de dados no nível de byte ou bit.

Exemplo

Temos um arquivo de dados de texto 'myfile.txt' salvo em nosso diretório de trabalho. O arquivo armazena dados de precipitação por três meses; Junho, julho e agosto para o ano de 2012.

Os dados em myfile.txt contêm conjuntos repetidos de medições de tempo, mês e precipitação em cinco locais. Os dados do cabeçalho armazenam o número de meses M; então temos M conjuntos de medidas.

O arquivo se parece com este -

Rainfall Data
Months: June, July, August
 
M = 3
12:00:00
June-2012
17.21  28.52  39.78  16.55 23.67
19.15  0.35   17.57  NaN   12.01
17.92  28.49  17.40  17.06 11.09
9.59   9.33   NaN    0.31  0.23 
10.46  13.17  NaN    14.89 19.33
20.97  19.50  17.65  14.45 14.00
18.23  10.34  17.95  16.46 19.34
09:10:02
July-2012
12.76  16.94  14.38  11.86 16.89
20.46  23.17  NaN    24.89 19.33
30.97  49.50  47.65  24.45 34.00
18.23  30.34  27.95  16.46 19.34
30.46  33.17  NaN    34.89  29.33
30.97  49.50  47.65  24.45 34.00
28.67  30.34  27.95  36.46 29.34
15:03:40
August-2012
17.09  16.55  19.59  17.25 19.22
17.54  11.45  13.48  22.55 24.01
NaN    21.19  25.85  25.05 27.21
26.79  24.98  12.23  16.99 18.67
17.54  11.45  13.48  22.55 24.01
NaN    21.19  25.85  25.05 27.21
26.79  24.98  12.23  16.99 18.67

Vamos importar dados deste arquivo e exibir esses dados. Execute as seguintes etapas -

Abra o arquivo com fopen função e obter o identificador do arquivo.
Descreva os dados no arquivo com format specifiers, tal como '%s'para uma string,'%d'para um número inteiro, ou'%f'para um número de ponto flutuante.
Para pular caracteres literais no arquivo, inclua-os na descrição do formato. Para pular um campo de dados, use um asterisco ('*') no especificador.

Por exemplo, para ler os cabeçalhos e retornar o valor único para M, escrevemos -
```
M = fscanf(fid, '%*s %*s\n%*s %*s %*s %*s\nM=%d\n\n', 1);
```
Por padrão, fscanflê os dados de acordo com a nossa descrição de formato até não encontrar nenhuma correspondência para os dados ou chegar ao final do arquivo. Aqui, usaremos o loop for para ler 3 conjuntos de dados e, a cada vez, ele lerá 7 linhas e 5 colunas.
Criaremos uma estrutura chamada mydata na área de trabalho para armazenar os dados lidos do arquivo. Essa estrutura tem três campos - time , month e raindata array.

Crie um arquivo de script e digite o seguinte código nele -

filename = '/data/myfile.txt';
rows = 7;
cols = 5;
 
% open the file
fid = fopen(filename);
 
% read the file headers, find M (number of months)
M = fscanf(fid, '%*s %*s\n%*s %*s %*s %*s\nM=%d\n\n', 1);
 
% read each set of measurements
for n = 1:M
   mydata(n).time = fscanf(fid, '%s', 1);
   mydata(n).month = fscanf(fid, '%s', 1);
 
   % fscanf fills the array in column order,
   % so transpose the results
   mydata(n).raindata  = ...
      fscanf(fid, '%f', [rows, cols]);
end
for n = 1:M
   disp(mydata(n).time), disp(mydata(n).month)
   disp(mydata(n).raindata)
end
 
% close the file
fclose(fid);

Quando você executa o arquivo, ele exibe o seguinte resultado -

12:00:00
June-2012
   17.2100   17.5700   11.0900   13.1700   14.4500
   28.5200       NaN    9.5900       NaN   14.0000
   39.7800   12.0100    9.3300   14.8900   18.2300
   16.5500   17.9200       NaN   19.3300   10.3400
   23.6700   28.4900    0.3100   20.9700   17.9500
   19.1500   17.4000    0.2300   19.5000   16.4600
   0.3500   17.0600   10.4600   17.6500   19.3400

09:10:02
July-2012
   12.7600       NaN   34.0000   33.1700   24.4500
   16.9400   24.8900   18.2300       NaN   34.0000
   14.3800   19.3300   30.3400   34.8900   28.6700
   11.8600   30.9700   27.9500   29.3300   30.3400
   16.8900   49.5000   16.4600   30.9700   27.9500
   20.4600   47.6500   19.3400   49.5000   36.4600
   23.1700   24.4500   30.4600   47.6500   29.3400

15:03:40
August-2012
   17.0900   13.4800   27.2100   11.4500   25.0500
   16.5500   22.5500   26.7900   13.4800   27.2100
   19.5900   24.0100   24.9800   22.5500   26.7900
   17.2500       NaN   12.2300   24.0100   24.9800
   19.2200   21.1900   16.9900       NaN   12.2300
   17.5400   25.8500   18.6700   21.1900   16.9900
   11.4500   25.0500   17.5400   25.8500   18.6700

A exportação (ou saída) de dados em MATLAB significa escrever em arquivos. O MATLAB permite que você use seus dados em outro aplicativo que lê arquivos ASCII. Para isso, o MATLAB oferece várias opções de exportação de dados.

Você pode criar os seguintes tipos de arquivos -

Arquivo de dados ASCII retangular e delimitado de uma matriz.
Arquivo de diário (ou registro) de pressionamentos de tecla e a saída de texto resultante.
Arquivo ASCII especializado usando funções de baixo nível, como fprintf.
Arquivo MEX para acessar sua rotina C / C ++ ou Fortran que grava em um formato de arquivo de texto específico.

Além disso, você também pode exportar dados para planilhas.

Existem duas maneiras de exportar uma matriz numérica como um arquivo de dados ASCII delimitado -

Usando o save função e especificando o -ascii qualificador
Usando o dlmwrite função

A sintaxe para usar a função salvar é -

save my_data.out num_array -ascii

onde my_data.out é o arquivo de dados ASCII delimitado criado, num_array é uma matriz numérica e−ascii é o especificador.

Sintaxe para usar o dlmwrite função é -

dlmwrite('my_data.out', num_array, 'dlm_char')

onde, my_data.out é o arquivo de dados ASCII delimitado criado, num_array é uma matriz numérica e dlm_char é o caractere delimitador.

Exemplo

O exemplo a seguir demonstra o conceito. Crie um arquivo de script e digite o seguinte código -

num_array = [ 1 2 3 4 ; 4 5 6 7; 7 8 9 0];
save array_data1.out num_array -ascii;
type array_data1.out
dlmwrite('array_data2.out', num_array, ' ');
type array_data2.out

Quando você executa o arquivo, ele exibe o seguinte resultado -

1.0000000e+00   2.0000000e+00   3.0000000e+00   4.0000000e+00
   4.0000000e+00   5.0000000e+00   6.0000000e+00   7.0000000e+00
   7.0000000e+00   8.0000000e+00   9.0000000e+00   0.0000000e+00

1 2 3 4
4 5 6 7
7 8 9 0

Observe que o comando save -ascii e a função dlmwrite não funcionam com matrizes de células como entrada. Para criar um arquivo ASCII delimitado a partir do conteúdo de uma matriz de células, você pode

Ou converta a matriz de células em uma matriz usando o cell2mat função
Ou exporte a matriz de células usando funções de E / S de arquivo de baixo nível.

Se você usar o save para gravar uma matriz de caracteres em um arquivo ASCII, ela grava o equivalente em ASCII dos caracteres no arquivo.

Por exemplo, vamos escrever a palavra 'olá' em um arquivo -

h = 'hello';
save textdata.out h -ascii
type textdata.out

O MATLAB executa as instruções acima e exibe o seguinte resultado. que são os caracteres da string 'hello' no formato ASCII de 8 dígitos.

1.0400000e+02   1.0100000e+02   1.0800000e+02   1.0800000e+02   1.1100000e+02

Escrevendo em arquivos de diário

Arquivos de diário são registros de atividades de sua sessão do MATLAB. A função de diário cria uma cópia exata de sua sessão em um arquivo de disco, excluindo gráficos.

Para ligar a função de diário, digite -

diary

Opcionalmente, você pode fornecer o nome do arquivo de log, por exemplo -

diary logdata.out

Para desligar a função de diário -

diary off

Você pode abrir o arquivo do diário em um editor de texto.

Exportando dados para arquivos de dados de texto com E / S de baixo nível

Até agora, exportamos matrizes numéricas. No entanto, você pode precisar criar outros arquivos de texto, incluindo combinações de dados numéricos e de caracteres, arquivos de saída não retangulares ou arquivos com esquemas de codificação não ASCII. Para esses fins, o MATLAB fornece o baixo nívelfprintf função.

Como nas atividades de arquivo de E / S de baixo nível, antes de exportar, você precisa abrir ou criar um arquivo com o fopenfunção e obter o identificador do arquivo. Por padrão, fopen abre um arquivo para acesso somente leitura. Você deve especificar a permissão para escrever ou acrescentar, como 'w' ou 'a'.

Depois de processar o arquivo, você precisa fechá-lo com fclose(fid) função.

O exemplo a seguir demonstra o conceito -

Exemplo

Crie um arquivo de script e digite o seguinte código nele -

% create a matrix y, with two rows
x = 0:10:100;
y = [x; log(x)];
 
% open a file for writing
fid = fopen('logtable.txt', 'w');
 
% Table Header
fprintf(fid, 'Log     Function\n\n');
 
% print values in column order
% two values appear on each row of the file
fprintf(fid, '%f    %f\n', y);
fclose(fid);

% display the file created
type logtable.txt

Quando você executa o arquivo, ele exibe o seguinte resultado -

Log         Function

0.000000    -Inf
10.000000    2.302585
20.000000    2.995732
30.000000    3.401197
40.000000    3.688879
50.000000    3.912023
60.000000    4.094345
70.000000    4.248495
80.000000    4.382027
90.000000    4.499810
100.000000    4.605170

Para traçar o gráfico de uma função, você precisa seguir os seguintes passos -

Definir x, especificando o range of values para a variável x, para o qual a função deve ser traçada
Defina a função, y = f(x)
Ligar para plot comando, como plot(x, y)

O exemplo a seguir demonstraria o conceito. Deixe-nos representar graficamente a função simplesy = x para o intervalo de valores para x de 0 a 100, com um incremento de 5.

Crie um arquivo de script e digite o seguinte código -

x = [0:5:100];
y = x;
plot(x, y)

Quando você executa o arquivo, o MATLAB exibe o seguinte gráfico -

Tomemos mais um exemplo para plotar a função y = x ² . Neste exemplo, desenharemos dois gráficos com a mesma função, mas no segundo momento, reduziremos o valor do incremento. Observe que, à medida que diminuímos o incremento, o gráfico se torna mais uniforme.

Crie um arquivo de script e digite o seguinte código -

x = [1 2 3 4 5 6 7 8 9 10];
x = [-100:20:100];
y = x.^2;
plot(x, y)

Quando você executa o arquivo, o MATLAB exibe o seguinte gráfico -

Altere um pouco o arquivo de código, reduza o incremento para 5 -

x = [-100:5:100];
y = x.^2;
plot(x, y)

MATLAB desenha um gráfico mais suave -

Adicionando título, rótulos, linhas de grade e escala no gráfico

O MATLAB permite adicionar títulos, rótulos ao longo dos eixos xey, linhas de grade e também ajustar os eixos para enfeitar o gráfico.

o xlabel e ylabel comandos geram rótulos ao longo do eixo xe do eixo y.
o title comando permite que você coloque um título no gráfico.
o grid on comando permite que você coloque as linhas de grade no gráfico.
o axis equal comando permite gerar o gráfico com os mesmos fatores de escala e os espaços em ambos os eixos.
o axis square comando gera um gráfico quadrado.

Exemplo

Crie um arquivo de script e digite o seguinte código -

x = [0:0.01:10];
y = sin(x);
plot(x, y), xlabel('x'), ylabel('Sin(x)'), title('Sin(x) Graph'),
grid on, axis equal

O MATLAB gera o seguinte gráfico -

Desenho de múltiplas funções no mesmo gráfico

Você pode desenhar vários gráficos no mesmo gráfico. O exemplo a seguir demonstra o conceito -

Exemplo

Crie um arquivo de script e digite o seguinte código -

x = [0 : 0.01: 10];
y = sin(x);
g = cos(x);
plot(x, y, x, g, '.-'), legend('Sin(x)', 'Cos(x)')

O MATLAB gera o seguinte gráfico -

Definição de cores no gráfico

O MATLAB oferece oito opções básicas de cores para desenhar gráficos. A tabela a seguir mostra as cores e seus códigos -

Código	Cor
W	Branco
k	Preto
b	Azul
r	Vermelho
c	Ciano
g	Verde
m	Magenta
y	Amarelo

Exemplo

Vamos desenhar o gráfico de dois polinômios

f (x) = 3x ⁴ + 2x ³ + 7x ² + 2x + 9 e
g (x) = 5x ³ + 9x + 2

Crie um arquivo de script e digite o seguinte código -

x = [-10 : 0.01: 10];
y = 3*x.^4 + 2 * x.^3 + 7 * x.^2 + 2 * x + 9;
g = 5 * x.^3 + 9 * x + 2;
plot(x, y, 'r', x, g, 'g')

Quando você executa o arquivo, o MATLAB gera o seguinte gráfico -

Configurando escalas de eixo

o axiscomando permite que você defina as escalas do eixo. Você pode fornecer valores mínimos e máximos para os eixos xey usando o comando de eixo da seguinte maneira -

axis ( [xmin xmax ymin ymax] )

O exemplo a seguir mostra isso -

Exemplo

Crie um arquivo de script e digite o seguinte código -

x = [0 : 0.01: 10];
y = exp(-x).* sin(2*x + 3);
plot(x, y), axis([0 10 -1 1])

Quando você executa o arquivo, o MATLAB gera o seguinte gráfico -

Gerando subtramas

Quando você cria uma matriz de plotagens na mesma figura, cada uma dessas plotagens é chamada de subtrama. osubplot comando é usado para criar subtramas.

A sintaxe do comando é -

subplot(m, n, p)

onde, m e n são o número de linhas e colunas da matriz do gráfico e p especifica onde colocar um gráfico particular.

Cada plotagem criada com o comando subplot pode ter suas próprias características. O exemplo a seguir demonstra o conceito -

Exemplo

Vamos gerar dois gráficos -

y = e ^−1,5x sen (10x)

y = e ^−2x sen (10x)

Crie um arquivo de script e digite o seguinte código -

x = [0:0.01:5];
y = exp(-1.5*x).*sin(10*x);
subplot(1,2,1)
plot(x,y), xlabel('x'),ylabel('exp(–1.5x)*sin(10x)'),axis([0 5 -1 1])
y = exp(-2*x).*sin(10*x);
subplot(1,2,2)
plot(x,y),xlabel('x'),ylabel('exp(–2x)*sin(10x)'),axis([0 5 -1 1])

Quando você executa o arquivo, o MATLAB gera o seguinte gráfico -

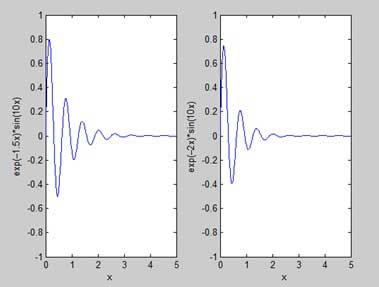
Este capítulo continuará explorando os recursos de plotagem e gráficos do MATLAB. Vamos discutir -

Desenho de gráficos de barras
Desenho de contornos
Gráficos tridimensionais

Desenho de gráficos de barras

o barcomando desenha um gráfico de barras bidimensional. Tomemos um exemplo para demonstrar a ideia.

Exemplo

Vamos ter uma sala de aula imaginária com 10 alunos. Sabemos que a porcentagem de notas obtidas por esses alunos são 75, 58, 90, 87, 50, 85, 92, 75, 60 e 95. Faremos o gráfico de barras para esses dados.

Crie um arquivo de script e digite o seguinte código -

x = [1:10];
y = [75, 58, 90, 87, 50, 85, 92, 75, 60, 95];
bar(x,y), xlabel('Student'),ylabel('Score'),
title('First Sem:')
print -deps graph.eps

Quando você executa o arquivo, o MATLAB exibe o seguinte gráfico de barras -

Desenho de Contornos

Uma linha de contorno de uma função de duas variáveis é uma curva ao longo da qual a função tem um valor constante. Linhas de contorno são usadas para criar mapas de contorno unindo pontos de elevação igual acima de um determinado nível, como o nível médio do mar.

O MATLAB fornece um contour função para desenhar mapas de contorno.

Exemplo

Vamos gerar um mapa de contorno que mostra as linhas de contorno para uma dada função g = f (x, y). Esta função possui duas variáveis. Portanto, teremos que gerar duas variáveis independentes, ou seja, dois conjuntos de dados x e y. Isso é feito chamando omeshgrid comando.

o meshgrid comando é usado para gerar uma matriz de elementos que fornecem o intervalo sobre xey junto com a especificação de incremento em cada caso.

Deixe-nos plotar nossa função g = f (x, y), onde −5 ≤ x ≤ 5, −3 ≤ y ≤ 3. Vamos tomar um incremento de 0,1 para ambos os valores. As variáveis são definidas como -

[x,y] = meshgrid(–5:0.1:5, –3:0.1:3);

Por último, precisamos atribuir a função. Deixe nossa função ser: x ² + y ²

Crie um arquivo de script e digite o seguinte código -

[x,y] = meshgrid(-5:0.1:5,-3:0.1:3);   %independent variables
g = x.^2 + y.^2;                       % our function
contour(x,y,g)                         % call the contour function
print -deps graph.eps

Quando você executa o arquivo, o MATLAB exibe o seguinte mapa de contorno -

Vamos modificar o código um pouco para enfeitar o mapa

[x,y] = meshgrid(-5:0.1:5,-3:0.1:3);   %independent variables
g = x.^2 + y.^2;                       % our function
[C, h] = contour(x,y,g);               % call the contour function
set(h,'ShowText','on','TextStep',get(h,'LevelStep')*2)
print -deps graph.eps

Quando você executa o arquivo, o MATLAB exibe o seguinte mapa de contorno -

Gráficos tridimensionais

Os gráficos tridimensionais basicamente exibem uma superfície definida por uma função em duas variáveis, g = f (x, y).

Como antes, para definir g, primeiro criamos um conjunto de pontos (x, y) sobre o domínio da função usando o meshgridcomando. Em seguida, atribuímos a própria função. Finalmente, usamos osurf comando para criar uma plotagem de superfície.

O exemplo a seguir demonstra o conceito -

Exemplo

Vamos criar um mapa de superfície 3D para a função g = xe ^{- (x ² + y ² )}

Crie um arquivo de script e digite o seguinte código -

[x,y] = meshgrid(-2:.2:2);
g = x .* exp(-x.^2 - y.^2);
surf(x, y, g)
print -deps graph.eps

Quando você executa o arquivo, o MATLAB exibe o seguinte mapa 3-D -

Você também pode usar o meshcomando para gerar uma superfície tridimensional. No entanto, osurf comando exibe as linhas de conexão e as faces da superfície em cores, enquanto o mesh comando cria uma superfície wireframe com linhas coloridas conectando os pontos de definição.

Até agora, vimos que todos os exemplos funcionam no MATLAB assim como no GNU, alternativamente chamado de Octave. Mas para resolver as equações algébricas básicas, tanto o MATLAB quanto o Octave são um pouco diferentes, então tentaremos cobrir o MATLAB e o Octave em seções separadas.

Também discutiremos a fatoração e a simplificação de expressões algébricas.

Resolvendo Equações Algébricas Básicas no MATLAB

o solvefunção é usada para resolver equações algébricas. Em sua forma mais simples, a função solve leva a equação entre aspas como um argumento.

Por exemplo, vamos resolver para x na equação x-5 = 0

solve('x-5=0')

O MATLAB executará a instrução acima e retornará o seguinte resultado -

ans =
   5

Você também pode chamar a função resolver como -

y = solve('x-5 = 0')

O MATLAB executará a instrução acima e retornará o seguinte resultado -

y =
   5

Você pode até não incluir o lado direito da equação -

solve('x-5')

O MATLAB executará a instrução acima e retornará o seguinte resultado -

ans =
   5

Se a equação envolver vários símbolos, o MATLAB por padrão assume que você está resolvendo para x, no entanto, a função de resolução tem outra forma -

solve(equation, variable)

onde, você também pode mencionar a variável.

Por exemplo, vamos resolver a equação v - u - 3t ² = 0, para v. Neste caso, devemos escrever -

solve('v-u-3*t^2=0', 'v')

O MATLAB executará a instrução acima e retornará o seguinte resultado -

ans =
   3*t^2 + u

Resolvendo Equações Algébricas Básicas em Oitava

o roots função é usada para resolver equações algébricas no Octave e você pode escrever os exemplos acima da seguinte maneira -

Por exemplo, vamos resolver para x na equação x-5 = 0

roots([1, -5])

O Octave irá executar a instrução acima e retornar o seguinte resultado -

ans = 5

Você também pode chamar a função resolver como -

y = roots([1, -5])

O Octave irá executar a instrução acima e retornar o seguinte resultado -

y = 5

Resolvendo Equações Quadráticas no MATLAB

o solvefunção também pode resolver equações de ordem superior. Geralmente é usado para resolver equações quadráticas. A função retorna as raízes da equação em uma matriz.

O exemplo a seguir resolve a equação quadrática x ² -7x +12 = 0. Crie um arquivo de script e digite o seguinte código -

eq = 'x^2 -7*x + 12 = 0';
s = solve(eq);
disp('The first root is: '), disp(s(1));
disp('The second root is: '), disp(s(2));

Quando você executa o arquivo, ele exibe o seguinte resultado -

The first root is: 
   3
The second root is: 
   4

Resolvendo Equações Quadráticas em Oitava

O exemplo a seguir resolve a equação quadrática x ² -7x +12 = 0 na oitava. Crie um arquivo de script e digite o seguinte código -

s = roots([1, -7, 12]);

disp('The first root is: '), disp(s(1));
disp('The second root is: '), disp(s(2));

Quando você executa o arquivo, ele exibe o seguinte resultado -

The first root is: 
   4
The second root is: 
   3

Resolvendo Equações de Ordem Superior no MATLAB

o solvefunção também pode resolver equações de ordem superior. Por exemplo, vamos resolver uma equação cúbica como (x-3) ² (x-7) = 0

solve('(x-3)^2*(x-7)=0')

O MATLAB executará a instrução acima e retornará o seguinte resultado -

No caso de equações de ordem superior, as raízes são longas, contendo muitos termos. Você pode obter o valor numérico dessas raízes convertendo-as para o dobro. O exemplo a seguir resolve a equação de quarta ordem x ⁴ - 7x ³ + 3x ² - 5x + 9 = 0.

Crie um arquivo de script e digite o seguinte código -

eq = 'x^4 - 7*x^3 + 3*x^2 - 5*x + 9 = 0';
s = solve(eq);
disp('The first root is: '), disp(s(1));
disp('The second root is: '), disp(s(2));
disp('The third root is: '), disp(s(3));
disp('The fourth root is: '), disp(s(4));

% converting the roots to double type
disp('Numeric value of first root'), disp(double(s(1)));
disp('Numeric value of second root'), disp(double(s(2)));
disp('Numeric value of third root'), disp(double(s(3)));
disp('Numeric value of fourth root'), disp(double(s(4)));

Quando você executa o arquivo, ele retorna o seguinte resultado -

The first root is: 
6.630396332390718431485053218985
 The second root is: 
1.0597804633025896291682772499885
 The third root is: 
- 0.34508839784665403032666523448675 - 1.0778362954630176596831109269793*i
 The fourth root is: 
- 0.34508839784665403032666523448675 + 1.0778362954630176596831109269793*i
Numeric value of first root
   6.6304
Numeric value of second root
   1.0598
Numeric value of third root
   -0.3451 - 1.0778i
Numeric value of fourth root
   -0.3451 + 1.0778i

Observe que as duas últimas raízes são números complexos.

Resolvendo Equações de Ordem Superior em Oitava

O exemplo a seguir resolve a equação de quarta ordem x ⁴ - 7x ³ + 3x ² - 5x + 9 = 0.

Crie um arquivo de script e digite o seguinte código -

v = [1, -7,  3, -5, 9];
s = roots(v);

% converting the roots to double type
disp('Numeric value of first root'), disp(double(s(1)));
disp('Numeric value of second root'), disp(double(s(2)));
disp('Numeric value of third root'), disp(double(s(3)));
disp('Numeric value of fourth root'), disp(double(s(4)));

Quando você executa o arquivo, ele retorna o seguinte resultado -

Numeric value of first root
 6.6304
Numeric value of second root
-0.34509 + 1.07784i
Numeric value of third root
-0.34509 - 1.07784i
Numeric value of fourth root
 1.0598

Resolvendo Sistema de Equações no MATLAB

o solveA função também pode ser usada para gerar soluções de sistemas de equações envolvendo mais de uma variável. Tomemos um exemplo simples para demonstrar esse uso.

Vamos resolver as equações -

5x + 9y = 5

3x - 6y = 4

Crie um arquivo de script e digite o seguinte código -

s = solve('5*x + 9*y = 5','3*x - 6*y = 4');
s.x
s.y

Quando você executa o arquivo, ele exibe o seguinte resultado -

ans =
   22/19
ans =
   -5/57

Da mesma forma, você pode resolver sistemas lineares maiores. Considere o seguinte conjunto de equações -

x + 3y -2z = 5

3x + 5y + 6z = 7

2x + 4y + 3z = 8

Resolvendo Sistema de Equações em Oitava

Temos uma abordagem um pouco diferente para resolver um sistema de 'n' equações lineares em 'n' incógnitas. Tomemos um exemplo simples para demonstrar esse uso.

Vamos resolver as equações -

5x + 9y = 5

3x - 6y = 4

Tal sistema de equações lineares pode ser escrito como a equação de matriz única Ax = b, onde A é a matriz de coeficientes, b é o vetor coluna contendo o lado direito das equações lineares ex é o vetor coluna representando a solução como mostrado no programa abaixo -

Crie um arquivo de script e digite o seguinte código -

A = [5, 9; 3, -6];
b = [5;4];
A \ b

Quando você executa o arquivo, ele exibe o seguinte resultado -

ans =

   1.157895
  -0.087719

Da mesma forma, você pode resolver sistemas lineares maiores conforme mostrado abaixo -

x + 3y -2z = 5

3x + 5y + 6z = 7

2x + 4y + 3z = 8

Expandindo e coletando equações no MATLAB

o expand e a collectfunção expande e coleta uma equação respectivamente. O exemplo a seguir demonstra os conceitos -

Ao trabalhar com muitas funções simbólicas, você deve declarar que suas variáveis são simbólicas.

Crie um arquivo de script e digite o seguinte código -

syms x   %symbolic variable x
syms y   %symbolic variable x
% expanding equations
expand((x-5)*(x+9))
expand((x+2)*(x-3)*(x-5)*(x+7))
expand(sin(2*x))
expand(cos(x+y))
 
% collecting equations
collect(x^3 *(x-7))
collect(x^4*(x-3)*(x-5))

Quando você executa o arquivo, ele exibe o seguinte resultado -

ans =
   x^2 + 4*x - 45
ans =
   x^4 + x^3 - 43*x^2 + 23*x + 210
ans =
   2*cos(x)*sin(x)
ans =
   cos(x)*cos(y) - sin(x)*sin(y)
ans =
   x^4 - 7*x^3
ans =
   x^6 - 8*x^5 + 15*x^4

Expandindo e coletando equações na oitava

Você precisa ter symbolic pacote, que fornece expand e a collectfunção para expandir e coletar uma equação, respectivamente. O exemplo a seguir demonstra os conceitos -

Quando você trabalha com muitas funções simbólicas, deve declarar que suas variáveis são simbólicas, mas o Octave tem uma abordagem diferente para definir variáveis simbólicas. Observe o uso deSin e Cos, que também são definidos no pacote simbólico.

Crie um arquivo de script e digite o seguinte código -

% first of all load the package, make sure its installed.
pkg load symbolic

% make symbols module available
symbols

% define symbolic variables
x = sym ('x');
y = sym ('y');
z = sym ('z');

% expanding equations
expand((x-5)*(x+9))
expand((x+2)*(x-3)*(x-5)*(x+7))
expand(Sin(2*x))
expand(Cos(x+y))
 
% collecting equations
collect(x^3 *(x-7), z)
collect(x^4*(x-3)*(x-5), z)

Quando você executa o arquivo, ele exibe o seguinte resultado -

ans =

-45.0+x^2+(4.0)*x
ans =

210.0+x^4-(43.0)*x^2+x^3+(23.0)*x
ans =

sin((2.0)*x)
ans =

cos(y+x)
ans =

x^(3.0)*(-7.0+x)
ans =

(-3.0+x)*x^(4.0)*(-5.0+x)

Fatoração e simplificação de expressões algébricas

o factor função fatoriza uma expressão e o simplifyfunção simplifica uma expressão. O exemplo a seguir demonstra o conceito -

Exemplo

Crie um arquivo de script e digite o seguinte código -

syms x
syms y
factor(x^3 - y^3)
factor([x^2-y^2,x^3+y^3])
simplify((x^4-16)/(x^2-4))

Quando você executa o arquivo, ele exibe o seguinte resultado -

ans =
   (x - y)*(x^2 + x*y + y^2)
ans =
   [ (x - y)*(x + y), (x + y)*(x^2 - x*y + y^2)]
ans =
   x^2 + 4

O MATLAB fornece várias maneiras de resolver problemas de cálculo diferencial e integral, resolvendo equações diferenciais de qualquer grau e cálculo de limites. O melhor de tudo é que você pode traçar facilmente os gráficos de funções complexas e verificar máximos, mínimos e outros pontos fixos em um gráfico resolvendo a função original, bem como sua derivada.

Este capítulo tratará de problemas de cálculo. Neste capítulo, discutiremos os conceitos de pré-cálculo, isto é, calcular os limites das funções e verificar as propriedades dos limites.

No próximo capítulo Diferencial , calcularemos a derivada de uma expressão e encontraremos os máximos e mínimos locais em um gráfico. Também discutiremos a resolução de equações diferenciais.

Finalmente, no capítulo Integração , discutiremos o cálculo integral.

Limites de cálculo

MATLAB fornece o limitfunção de cálculo de limites. Em sua forma mais básica, olimit A função recebe a expressão como argumento e encontra o limite da expressão quando a variável independente vai para zero.

Por exemplo, vamos calcular o limite de uma função f (x) = (x ³ + 5) / (x ⁴ + 7), já que x tende a zero.

syms x
limit((x^3 + 5)/(x^4 + 7))

O MATLAB executará a instrução acima e retornará o seguinte resultado -

ans =
   5/7

A função limite cai no reino da computação simbólica; você precisa usar osymsfunção para dizer ao MATLAB quais variáveis simbólicas você está usando. Você também pode calcular o limite de uma função, pois a variável tende a algum número diferente de zero. Para calcular lim _{x-> a} (f (x)), usamos o comando limit com argumentos. O primeiro é a expressão e o segundo é o número, que se aproxima de x , aqui é a .

Por exemplo, vamos calcular o limite de uma função f (x) = (x-3) / (x-1), pois x tende a 1.

limit((x - 3)/(x-1),1)

O MATLAB executará a instrução acima e retornará o seguinte resultado -

ans =
   NaN

Vamos dar outro exemplo,

limit(x^2 + 5, 3)

O MATLAB executará a instrução acima e retornará o seguinte resultado -

ans =
   14

Cálculo de limites usando oitava

A seguir está a versão Octave do exemplo acima usando symbolic pacote, tente executar e comparar o resultado -

pkg load symbolic
symbols

x = sym("x");
subs((x^3+5)/(x^4+7),x,0)

O Octave irá executar a instrução acima e retornar o seguinte resultado -

ans =
   0.7142857142857142857

Verificação das propriedades básicas dos limites

O Teorema Algébrico do Limite fornece algumas propriedades básicas dos limites. Estes são os seguintes -

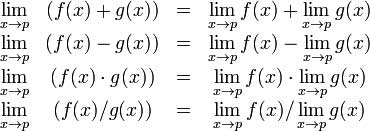
Vamos considerar duas funções -

f (x) = (3x + 5) / (x - 3)
g (x) = x ² + 1.

Vamos calcular os limites das funções como x tende a 5, de ambas as funções e verificar as propriedades básicas dos limites usando essas duas funções e o MATLAB.

Exemplo

Crie um arquivo de script e digite o seguinte código nele -

syms x
f = (3*x + 5)/(x-3);
g = x^2 + 1;
l1 = limit(f, 4)
l2 = limit (g, 4)
lAdd = limit(f + g, 4)
lSub = limit(f - g, 4)
lMult = limit(f*g, 4)
lDiv = limit (f/g, 4)

Quando você executa o arquivo, ele exibe -

l1 =
   17
  
l2 =
   17
  
lAdd =
   34
 
lSub =
   0
  
lMult =
   289
  
lDiv =
   1

Verificação das propriedades básicas dos limites usando oitava

A seguir está a versão Octave do exemplo acima usando symbolic pacote, tente executar e comparar o resultado -

pkg load symbolic
symbols

x = sym("x");
f = (3*x + 5)/(x-3);
g = x^2 + 1;

l1 = subs(f, x, 4)
l2 = subs (g, x, 4)
lAdd = subs (f+g, x, 4)
lSub = subs (f-g, x, 4)
lMult = subs (f*g, x, 4)
lDiv = subs (f/g, x, 4)

O Octave irá executar a instrução acima e retornar o seguinte resultado -

l1 =
   17.0
l2 =
   17.0
lAdd =
   34.0
lSub =
   0.0
lMult =
   289.0
lDiv =
   1.0

Limites do lado esquerdo e direito

Quando uma função tem uma descontinuidade para algum valor particular da variável, o limite não existe naquele ponto. Em outras palavras, os limites de uma função f (x) tem descontinuidade em x = a, quando o valor do limite, conforme x se aproxima de x do lado esquerdo, não é igual ao valor do limite quando x se aproxima do lado direito.

Isso leva ao conceito de limites para canhotos e destros. Um limite para canhotos é definido como o limite quando x -> a, da esquerda, ou seja, x se aproxima de a, para valores de x <a. Um limite para destros é definido como o limite quando x -> a, da direita, ou seja, x se aproxima de a, para valores de x> a. Quando o limite para canhotos e o limite para destros não são iguais, o limite não existe.

Vamos considerar uma função -

f(x) = (x - 3)/|x - 3|

Mostraremos que lim _{x-> 3} f (x) não existe. O MATLAB nos ajuda a estabelecer esse fato de duas maneiras -

Traçando o gráfico da função e mostrando a descontinuidade.
Calculando os limites e mostrando que ambos são diferentes.

Os limites para canhotos e destros são calculados passando as cadeias de caracteres 'esquerda' e 'direita' para o comando limit como último argumento.

Exemplo

Crie um arquivo de script e digite o seguinte código nele -

f = (x - 3)/abs(x-3);
ezplot(f,[-1,5])
l = limit(f,x,3,'left')
r = limit(f,x,3,'right')

Quando você executa o arquivo, o MATLAB desenha o seguinte gráfico

Depois que a seguinte saída for exibida -

l =
   -1
  
r =
   1

MATLAB fornece o diffcomando para calcular derivados simbólicos. Em sua forma mais simples, você passa a função que deseja diferenciar para o comando diff como um argumento.

Por exemplo, vamos calcular a derivada da função f (t) = 3t ² + 2t ^-2

Exemplo

Crie um arquivo de script e digite o seguinte código nele -

syms t
f = 3*t^2 + 2*t^(-2);
diff(f)

Quando o código acima é compilado e executado, ele produz o seguinte resultado -

ans =
6*t - 4/t^3

A seguir está o oitavo equivalente do cálculo acima -

pkg load symbolic
symbols

t = sym("t");
f = 3*t^2 + 2*t^(-2);
differentiate(f,t)

Octave executa o código e retorna o seguinte resultado -

ans =
   -(4.0)*t^(-3.0)+(6.0)*t

Verificação de regras elementares de diferenciação

Vamos enunciar brevemente várias equações ou regras para diferenciação de funções e verificar essas regras. Para este propósito, escreveremos f '(x) para uma derivada de primeira ordem ef "(x) para uma derivada de segunda ordem.

A seguir estão as regras de diferenciação -

Regra 1

Para quaisquer funções feg e quaisquer números reais a e b são a derivada da função -

h(x) = af(x) + bg(x) em relação ax é dado por -

h'(x) = af'(x) + bg'(x)

Regra 2

o sum e subtraction as regras afirmam que se feg são duas funções, f 'e g' são suas derivadas, respectivamente, então,

(f + g)' = f' + g'

(f - g)' = f' - g'

Regra 3

o product regra afirma que se feg são duas funções, f 'e g' são suas derivadas, respectivamente, então,

(f.g)' = f'.g + g'.f

Regra 4

o quotient regra afirma que se feg são duas funções, f 'e g' são suas derivadas, respectivamente, então,

(f/g)' = (f'.g - g'.f)/g²

Regra 5

o polynomial ou regra de poder elementar afirma que, se y = f(x) = xⁿ, então f' = n. x^(n-1)

Um resultado direto desta regra é que a derivada de qualquer constante é zero, ou seja, se y = k, qualquer constante, então

f' = 0

Regra 6

o chain regra afirma que, derivada da função de uma função h(x) = f(g(x)) em relação ax é,

h'(x)= f'(g(x)).g'(x)

Exemplo

Crie um arquivo de script e digite o seguinte código nele -

syms x
syms t

f = (x + 2)*(x^2 + 3)
der1 = diff(f)
f = (t^2 + 3)*(sqrt(t) + t^3)
der2 = diff(f)
f = (x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2)
der3 = diff(f)
f = (2*x^2 + 3*x)/(x^3 + 1)
der4 = diff(f)
f = (x^2 + 1)^17
der5 = diff(f)
f = (t^3 + 3* t^2 + 5*t -9)^(-6)
der6 = diff(f)

Quando você executa o arquivo, o MATLAB exibe o seguinte resultado -

f =
   (x^2 + 3)*(x + 2)
 
   der1 =
   2*x*(x + 2) + x^2 + 3
  
f =
   (t^(1/2) + t^3)*(t^2 + 3)
 
   der2 =
   (t^2 + 3)*(3*t^2 + 1/(2*t^(1/2))) + 2*t*(t^(1/2) + t^3)
  
f =
   (x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2)
  
der3 =
   (2*x - 2)*(3*x^3 - 5*x^2 + 2) - (- 9*x^2 + 10*x)*(x^2 - 2*x + 1)
 
f =
   (2*x^2 + 3*x)/(x^3 + 1)
  
der4 =
   (4*x + 3)/(x^3 + 1) - (3*x^2*(2*x^2 + 3*x))/(x^3 + 1)^2
  
f =
   (x^2 + 1)^17
  
der5 =
   34*x*(x^2 + 1)^16
  
f =
   1/(t^3 + 3*t^2 + 5*t - 9)^6
  
der6 =
   -(6*(3*t^2 + 6*t + 5))/(t^3 + 3*t^2 + 5*t - 9)^7

A seguir está o oitavo equivalente do cálculo acima -

pkg load symbolic
symbols

x = sym("x");
t = sym("t");
f = (x + 2)*(x^2 + 3) 
der1 = differentiate(f,x) 
f = (t^2 + 3)*(t^(1/2) + t^3) 
der2 = differentiate(f,t) 
f = (x^2 - 2*x + 1)*(3*x^3 - 5*x^2 + 2) 
der3 = differentiate(f,x) 
f = (2*x^2 + 3*x)/(x^3 + 1) 
der4 = differentiate(f,x) 
f = (x^2 + 1)^17 
der5 = differentiate(f,x) 
f = (t^3 + 3* t^2 + 5*t -9)^(-6) 
der6 = differentiate(f,t)

Octave executa o código e retorna o seguinte resultado -

f =

(2.0+x)*(3.0+x^(2.0))
der1 =

3.0+x^(2.0)+(2.0)*(2.0+x)*x
f =

(t^(3.0)+sqrt(t))*(3.0+t^(2.0))
der2 =

(2.0)*(t^(3.0)+sqrt(t))*t+((3.0)*t^(2.0)+(0.5)*t^(-0.5))*(3.0+t^(2.0))
f =

(1.0+x^(2.0)-(2.0)*x)*(2.0-(5.0)*x^(2.0)+(3.0)*x^(3.0))
der3 =

(-2.0+(2.0)*x)*(2.0-(5.0)*x^(2.0)+(3.0)*x^(3.0))+((9.0)*x^(2.0)-(10.0)*x)*(1.0+x^(2.0)-(2.0)*x)
f =

(1.0+x^(3.0))^(-1)*((2.0)*x^(2.0)+(3.0)*x)
der4 =

(1.0+x^(3.0))^(-1)*(3.0+(4.0)*x)-(3.0)*(1.0+x^(3.0))^(-2)*x^(2.0)*((2.0)*x^(2.0)+(3.0)*x)
f =

(1.0+x^(2.0))^(17.0)
der5 =

(34.0)*(1.0+x^(2.0))^(16.0)*x
f =

(-9.0+(3.0)*t^(2.0)+t^(3.0)+(5.0)*t)^(-6.0)
der6 =

-(6.0)*(-9.0+(3.0)*t^(2.0)+t^(3.0)+(5.0)*t)^(-7.0)*(5.0+(3.0)*t^(2.0)+(6.0)*t)

Derivados de funções exponenciais, logarítmicas e trigonométricas

A tabela a seguir fornece os derivados de funções exponenciais, logarítmicas e trigonométricas comumente usadas -

Função	Derivado
c^a.x	c ^a.x .ln ca (ln é o logaritmo natural)
e^x	e ^x
ln x	1 / x
ln_cx	1 / x.ln c
x^x	x ^x . (1 + ln x)
sin(x)	cos (x)
cos(x)	-sin (x)
tan(x)	sec ² (x), ou 1 / cos ² (x), ou 1 + tan ² (x)
cot(x)	-csc ² (x), ou -1 / sen ² (x), ou - (1 + cot ² (x))
sec(x)	sec (x) .tan (x)
csc(x)	-csc (x) .cot (x)

Exemplo

Crie um arquivo de script e digite o seguinte código nele -

syms x
y = exp(x)
diff(y)
y = x^9
diff(y)
y = sin(x)
diff(y)
y = tan(x)
diff(y)
y = cos(x)
diff(y)
y = log(x)
diff(y)
y = log10(x)
diff(y)
y = sin(x)^2
diff(y)
y = cos(3*x^2 + 2*x + 1)
diff(y)
y = exp(x)/sin(x)
diff(y)

Quando você executa o arquivo, o MATLAB exibe o seguinte resultado -

y =
   exp(x)
   ans =
   exp(x)

y =
   x^9
   ans =
   9*x^8
  
y =
   sin(x)
   ans =
   cos(x)
  
y =
   tan(x)
   ans =
   tan(x)^2 + 1
 
y =
   cos(x)
   ans =
   -sin(x)
  
y =
   log(x)
   ans =
   1/x
  
y =
   log(x)/log(10)
   ans =
   1/(x*log(10))
 
y =
   sin(x)^2
   ans =
   2*cos(x)*sin(x)
 
y =
   cos(3*x^2 + 2*x + 1)
   ans =
   -sin(3*x^2 + 2*x + 1)*(6*x + 2)
  
y =
   exp(x)/sin(x)
   ans =
   exp(x)/sin(x) - (exp(x)*cos(x))/sin(x)^2

A seguir está o oitavo equivalente do cálculo acima -

pkg load symbolic
symbols

x = sym("x");
y = Exp(x)
differentiate(y,x)

y = x^9
differentiate(y,x)

y = Sin(x)
differentiate(y,x)

y = Tan(x)
differentiate(y,x)

y = Cos(x)
differentiate(y,x)

y = Log(x)
differentiate(y,x)

% symbolic packages does not have this support
%y = Log10(x)
%differentiate(y,x)

y = Sin(x)^2
differentiate(y,x)

y = Cos(3*x^2 + 2*x + 1)
differentiate(y,x)

y = Exp(x)/Sin(x)
differentiate(y,x)

Octave executa o código e retorna o seguinte resultado -

y =

exp(x)
ans =

exp(x)
y =

x^(9.0)
ans =

(9.0)*x^(8.0)
y =

sin(x)
ans =

cos(x)
y =

tan(x)
ans =

1+tan(x)^2
y =

cos(x)
ans =

-sin(x)
y =

log(x)
ans =

x^(-1)
y =

sin(x)^(2.0)
ans =

(2.0)*sin(x)*cos(x)
y =

cos(1.0+(2.0)*x+(3.0)*x^(2.0))
ans =

-(2.0+(6.0)*x)*sin(1.0+(2.0)*x+(3.0)*x^(2.0))
y =

sin(x)^(-1)*exp(x)
ans =

sin(x)^(-1)*exp(x)-sin(x)^(-2)*cos(x)*exp(x)

Computando Derivados de Ordem Superior

Para calcular derivados superiores de uma função f, usamos a sintaxe diff(f,n).

Vamos calcular a segunda derivada da função y = f (x) = x ^{.e -3x}

f = x*exp(-3*x);
diff(f, 2)

O MATLAB executa o código e retorna o seguinte resultado -

ans =
9*x*exp(-3*x) - 6*exp(-3*x)

A seguir está o oitavo equivalente do cálculo acima -

pkg load symbolic
symbols

x = sym("x");
f = x*Exp(-3*x);
differentiate(f, x, 2)

Octave executa o código e retorna o seguinte resultado -

ans =

(9.0)*exp(-(3.0)*x)*x-(6.0)*exp(-(3.0)*x)

Exemplo

Neste exemplo, vamos resolver um problema. Dado que uma funçãoy = f(x) = 3 sin(x) + 7 cos(5x). Teremos que descobrir se a equaçãof" + f = -5cos(2x) permanece verdadeiro.

Crie um arquivo de script e digite o seguinte código nele -

syms x
y = 3*sin(x)+7*cos(5*x);  % defining the function
lhs = diff(y,2)+y;        %evaluting the lhs of the equation
rhs = -5*cos(2*x);        %rhs of the equation
if(isequal(lhs,rhs))
   disp('Yes, the equation holds true');
else
   disp('No, the equation does not hold true');
end
disp('Value of LHS is: '), disp(lhs);

Quando você executa o arquivo, ele exibe o seguinte resultado -

No, the equation does not hold true
Value of LHS is: 
-168*cos(5*x)

A seguir está o oitavo equivalente do cálculo acima -

pkg load symbolic
symbols

x = sym("x");
y = 3*Sin(x)+7*Cos(5*x);           % defining the function
lhs = differentiate(y, x, 2) + y;  %evaluting the lhs of the equation
rhs = -5*Cos(2*x);                 %rhs of the equation

if(lhs == rhs)
   disp('Yes, the equation holds true');
else
   disp('No, the equation does not hold true');
end
disp('Value of LHS is: '), disp(lhs);

Octave executa o código e retorna o seguinte resultado -

No, the equation does not hold true
Value of LHS is: 
-(168.0)*cos((5.0)*x)

Encontrando o Máximo e o Mínimo de uma Curva

Se estivermos procurando pelos máximos e mínimos locais para um gráfico, estamos basicamente procurando pelos pontos mais altos ou mais baixos no gráfico da função em uma localidade particular, ou por uma faixa particular de valores da variável simbólica.

Para uma função y = f (x), os pontos no gráfico onde o gráfico tem inclinação zero são chamados stationary points. Em outras palavras, os pontos estacionários estão onde f '(x) = 0.

Para encontrar os pontos estacionários de uma função que diferenciamos, precisamos definir a derivada igual a zero e resolver a equação.

Exemplo

Vamos encontrar os pontos estacionários da função f (x) = 2x ³ + 3x ² - 12x + 17

Execute as seguintes etapas -

First let us enter the function and plot its graph.

syms x
y = 2*x^3 + 3*x^2 - 12*x + 17;   % defining the function
ezplot(y)

O MATLAB executa o código e retorna o seguinte gráfico -

Aqui está o código equivalente do Octave para o exemplo acima -

pkg load symbolic
symbols

x = sym('x');
y = inline("2*x^3 + 3*x^2 - 12*x + 17");

ezplot(y)
print -deps graph.eps

Our aim is to find some local maxima and minima on the graph, so let us find the local maxima and minima for the interval [-2, 2] on the graph.

syms x
y = 2*x^3 + 3*x^2 - 12*x + 17;   % defining the function
ezplot(y, [-2, 2])

O MATLAB executa o código e retorna o seguinte gráfico -

Aqui está o código equivalente do Octave para o exemplo acima -

pkg load symbolic
symbols

x = sym('x');
y = inline("2*x^3 + 3*x^2 - 12*x + 17");

ezplot(y, [-2, 2])
print -deps graph.eps

Next, let us compute the derivative.

g = diff(y)

O MATLAB executa o código e retorna o seguinte resultado -

g =
   6*x^2 + 6*x - 12

Aqui está o equivalente do Octave do cálculo acima -

pkg load symbolic
symbols

x = sym("x");
y = 2*x^3 + 3*x^2 - 12*x + 17;
g = differentiate(y,x)

Octave executa o código e retorna o seguinte resultado -

g =
   -12.0+(6.0)*x+(6.0)*x^(2.0)

Let us solve the derivative function, g, to get the values where it becomes zero.

s = solve(g)

O MATLAB executa o código e retorna o seguinte resultado -

s =
   1
   -2

A seguir está o oitavo equivalente do cálculo acima -

pkg load symbolic
symbols

x = sym("x");
y = 2*x^3 + 3*x^2 - 12*x + 17;
g = differentiate(y,x)
roots([6, 6, -12])

Octave executa o código e retorna o seguinte resultado -

g =

-12.0+(6.0)*x^(2.0)+(6.0)*x
ans =

  -2
   1

This agrees with our plot. So let us evaluate the function f at the critical points x = 1, -2. Podemos substituir um valor em uma função simbólica usando o subs comando.

subs(y, 1), subs(y, -2)

O MATLAB executa o código e retorna o seguinte resultado -

ans =
   10
ans =
   37

A seguir está o oitavo equivalente do cálculo acima -

pkg load symbolic
symbols

x = sym("x");
y = 2*x^3 + 3*x^2 - 12*x + 17;
g = differentiate(y,x)

roots([6, 6, -12])
subs(y, x, 1), subs(y, x, -2)

ans =
   10.0
ans =
   37.0-4.6734207789940138748E-18*I

Portanto, os valores mínimo e máximo na função f (x) = 2x ³ + 3x ² - 12x + 17, no intervalo [-2,2] são 10 e 37.

Resolvendo Equações Diferenciais

MATLAB fornece o dsolve comando para resolver equações diferenciais simbolicamente.

A forma mais básica do dsolve comando para encontrar a solução para uma única equação é

dsolve('eqn')

onde eqn é uma string de texto usada para inserir a equação.

Ele retorna uma solução simbólica com um conjunto de constantes arbitrárias que o MATLAB rotula C1, C2 e assim por diante.

Você também pode especificar as condições iniciais e de limite para o problema, como uma lista delimitada por vírgulas após a equação como -

dsolve('eqn','cond1', 'cond2',…)

Para o propósito de usar o comando dsolve, derivatives are indicated with a D. Por exemplo, uma equação como f '(t) = -2 * f + custo (t) é inserida como -

'Df = -2*f + cos(t)'

Derivadas mais altas são indicadas seguindo D pela ordem da derivada.

Por exemplo, a equação f "(x) + 2f '(x) = 5sin3x deve ser inserida como -

'D2y + 2Dy = 5*sin(3*x)'

Tomemos um exemplo simples de uma equação diferencial de primeira ordem: y '= 5y.

s = dsolve('Dy = 5*y')

O MATLAB executa o código e retorna o seguinte resultado -

s =
   C2*exp(5*t)

Tomemos outro exemplo de uma equação diferencial de segunda ordem como: y "- y = 0, y (0) = -1, y '(0) = 2.

dsolve('D2y - y = 0','y(0) = -1','Dy(0) = 2')

O MATLAB executa o código e retorna o seguinte resultado -

ans =
   exp(t)/2 - (3*exp(-t))/2

A integração lida com dois tipos de problemas essencialmente diferentes.

No primeiro tipo, a derivada de uma função é fornecida e queremos encontrar a função. Portanto, basicamente invertemos o processo de diferenciação. Este processo reverso é conhecido como antidiferenciação, ou encontrar a função primitiva, ou encontrar umindefinite integral.
O segundo tipo de problema envolve somar um número muito grande de quantidades muito pequenas e, então, estabelecer um limite quando o tamanho das quantidades se aproxima de zero, enquanto o número de termos tende ao infinito. Este processo leva à definição dodefinite integral.

Integrais definidos são usados para encontrar área, volume, centro de gravidade, momento de inércia, trabalho realizado por uma força e em inúmeras outras aplicações.

Encontrando Integral Indefinido Usando MATLAB

Por definição, se a derivada de uma função f (x) é f '(x), então dizemos que uma integral indefinida de f' (x) em relação a x é f (x). Por exemplo, como a derivada (em relação a x) de x ² é 2x, podemos dizer que uma integral indefinida de 2x é x ² .

Em símbolos -

f'(x²) = 2x, Portanto,

∫ 2xdx = x².

Integral indefinido não é único, porque a derivada de x ² + c, para qualquer valor de uma constante c, também será 2x.

Isso é expresso em símbolos como -

∫ 2xdx = x² + c.

Onde, c é chamado de 'constante arbitrária'.

O MATLAB fornece um intcomando para calcular a integral de uma expressão. Para derivar uma expressão para a integral indefinida de uma função, escrevemos -

int(f);

Por exemplo, do nosso exemplo anterior -

syms x 
int(2*x)

O MATLAB executa a instrução acima e retorna o seguinte resultado -

ans =
   x^2

Exemplo 1

Neste exemplo, vamos encontrar a integral de algumas expressões comumente usadas. Crie um arquivo de script e digite o seguinte código nele -

syms x n

int(sym(x^n))
f = 'sin(n*t)'
int(sym(f))
syms a t
int(a*cos(pi*t))
int(a^x)

Quando você executa o arquivo, ele exibe o seguinte resultado -

ans =
   piecewise([n == -1, log(x)], [n ~= -1, x^(n + 1)/(n + 1)])
f =
sin(n*t)
ans =
   -cos(n*t)/n
   ans =
   (a*sin(pi*t))/pi
   ans =
   a^x/log(a)

Exemplo 2

Crie um arquivo de script e digite o seguinte código nele -

syms x n
int(cos(x))
int(exp(x))
int(log(x))
int(x^-1)
int(x^5*cos(5*x))
pretty(int(x^5*cos(5*x)))
int(x^-5)
int(sec(x)^2)
pretty(int(1 - 10*x + 9 * x^2))
int((3 + 5*x -6*x^2 - 7*x^3)/2*x^2)
pretty(int((3 + 5*x -6*x^2 - 7*x^3)/2*x^2))

Observe que o pretty função retorna uma expressão em um formato mais legível.

Quando você executa o arquivo, ele exibe o seguinte resultado -

ans =
   sin(x)
 
ans =
   exp(x)
 
ans =
   x*(log(x) - 1)
 
ans =
   log(x)
 
ans =
(24*cos(5*x))/3125 + (24*x*sin(5*x))/625 - (12*x^2*cos(5*x))/125 + (x^4*cos(5*x))/5 - (4*x^3*sin(5*x))/25 + (x^5*sin(5*x))/5
                                    2             4 
   24 cos(5 x)   24 x sin(5 x)   12 x  cos(5 x)   x  cos(5 x) 
   ----------- + ------------- - -------------- + ------------ 
      3125            625             125              5 
   
        3             5 
 
   4 x  sin(5 x)   x  sin(5 x) 
   ------------- + ----------- 
         25              5
 
ans =
-1/(4*x^4)
 
ans =
tan(x)
        2 
  x (3 x  - 5 x + 1)
 
ans = 
- (7*x^6)/12 - (3*x^5)/5 + (5*x^4)/8 + x^3/2
 
      6      5      4    3 
    7 x    3 x    5 x    x 
  - ---- - ---- + ---- + -- 
     12     5      8     2

Encontrando Integral Definido Usando MATLAB

Por definição, integral definida é basicamente o limite de uma soma. Usamos integrais definidas para encontrar áreas como a área entre uma curva e o eixo xe a área entre duas curvas. Integrais definidos também podem ser usados em outras situações, onde a quantidade necessária pode ser expressa como o limite de uma soma.

o int A função pode ser usada para integração definida passando os limites sobre os quais você deseja calcular a integral.

Calcular

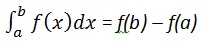
nós escrevemos,

int(x, a, b)

Por exemplo, para calcular o valor de

escrevemos -

int(x, 4, 9)

O MATLAB executa a instrução acima e retorna o seguinte resultado -

ans =
   65/2

A seguir está o oitavo equivalente do cálculo acima -

pkg load symbolic
symbols

x = sym("x");
f = x;
c = [1, 0];
integral = polyint(c);

a = polyval(integral, 9) - polyval(integral, 4);
display('Area: '), disp(double(a));

Octave executa o código e retorna o seguinte resultado -

Area: 

   32.500

Uma solução alternativa pode ser dada usando a função quad () fornecida pelo Octave como segue -

pkg load symbolic
symbols

f = inline("x");
[a, ierror, nfneval] = quad(f, 4, 9);

display('Area: '), disp(double(a));

Octave executa o código e retorna o seguinte resultado -

Area: 
   32.500

Exemplo 1

Vamos calcular a área delimitada entre o eixo xe a curva y = x ³ −2x + 5 e as ordenadas x = 1 e x = 2.

A área necessária é fornecida por -

Crie um arquivo de script e digite o seguinte código -

f = x^3 - 2*x +5;
a = int(f, 1, 2)
display('Area: '), disp(double(a));

Quando você executa o arquivo, ele exibe o seguinte resultado -

a =
23/4
Area: 
   5.7500

A seguir está o oitavo equivalente do cálculo acima -

pkg load symbolic
symbols

x = sym("x");
f = x^3 - 2*x +5;
c = [1, 0, -2, 5];
integral = polyint(c);

a = polyval(integral, 2) - polyval(integral, 1);
display('Area: '), disp(double(a));

Octave executa o código e retorna o seguinte resultado -

Area: 

   5.7500

Uma solução alternativa pode ser dada usando a função quad () fornecida pelo Octave como segue -

pkg load symbolic
symbols

x = sym("x");
f = inline("x^3 - 2*x +5");

[a, ierror, nfneval] = quad(f, 1, 2);
display('Area: '), disp(double(a));

Octave executa o código e retorna o seguinte resultado -

Area: 
   5.7500

Exemplo 2

Encontre a área sob a curva: f (x) = x ² cos (x) para −4 ≤ x ≤ 9.

Crie um arquivo de script e escreva o seguinte código -

f = x^2*cos(x);
ezplot(f, [-4,9])
a = int(f, -4, 9)
disp('Area: '), disp(double(a));

Quando você executa o arquivo, o MATLAB traça o gráfico -

O resultado é dado abaixo -

a = 
8*cos(4) + 18*cos(9) + 14*sin(4) + 79*sin(9)
 
Area: 
   0.3326

A seguir está o oitavo equivalente do cálculo acima -

pkg load symbolic
symbols

x = sym("x");
f = inline("x^2*cos(x)");

ezplot(f, [-4,9])
print -deps graph.eps

[a, ierror, nfneval] = quad(f, -4, 9);
display('Area: '), disp(double(a));

MATLAB representa polinômios como vetores de linha contendo coeficientes ordenados por potências descendentes. Por exemplo, a equação P (x) = x ⁴ + 7x ³ - 5x + 9 pode ser representada como -

p = [1 7 0 -5 9];

Avaliando Polinômios

o polyvalfunção é usada para avaliar um polinômio em um valor especificado. Por exemplo, para avaliar nosso polinômio anteriorp, em x = 4, digite -

p = [1 7 0  -5 9];
polyval(p,4)

O MATLAB executa as instruções acima e retorna o seguinte resultado -

ans = 693

O MATLAB também fornece o polyvalmfunção para avaliar um polinômio de matriz. Um polinômio de matriz é umpolynomial com matrizes como variáveis.

Por exemplo, vamos criar uma matriz quadrada X e avaliar o polinômio p, em X -

p = [1 7 0  -5 9];
X = [1 2 -3 4; 2 -5 6 3; 3 1 0 2; 5 -7 3 8];
polyvalm(p, X)

O MATLAB executa as instruções acima e retorna o seguinte resultado -

ans =
      2307       -1769        -939        4499
      2314       -2376        -249        4695
      2256       -1892        -549        4310
      4570       -4532       -1062        9269

Encontrando as raízes dos polinômios

o rootsfunção calcula as raízes de um polinômio. Por exemplo, para calcular as raízes do nosso polinômio p, digite -

p = [1 7 0  -5 9];
r = roots(p)

O MATLAB executa as instruções acima e retorna o seguinte resultado -

r =
   -6.8661 + 0.0000i
   -1.4247 + 0.0000i
   0.6454 + 0.7095i
   0.6454 - 0.7095i

A função polyé um inverso da função de raízes e retorna aos coeficientes polinomiais. Por exemplo -

p2 = poly(r)

O MATLAB executa as instruções acima e retorna o seguinte resultado -

p2 =

   Columns 1 through 3:

      1.00000 + 0.00000i   7.00000 + 0.00000i   0.00000 + 0.00000i

   Columns 4 and 5:

      -5.00000 - 0.00000i   9.00000 + 0.00000i

Ajuste de curva polinomial

o polyfitfunção encontra os coeficientes de um polinômio que se ajusta a um conjunto de dados no sentido de mínimos quadrados. Se x e y são dois vetores contendo os dados x e y a serem ajustados a um polinômio de n graus, então obtemos o polinômio ajustando os dados escrevendo -

p = polyfit(x,y,n)

Exemplo

Crie um arquivo de script e digite o seguinte código -

x = [1 2 3 4 5 6]; y = [5.5 43.1 128 290.7 498.4 978.67];   %data
p = polyfit(x,y,4)   %get the polynomial

% Compute the values of the polyfit estimate over a finer range, 
% and plot the estimate over the real data values for comparison:
x2 = 1:.1:6;          
y2 = polyval(p,x2);
plot(x,y,'o',x2,y2)
grid on

Quando você executa o arquivo, o MATLAB exibe o seguinte resultado -

p =
   4.1056  -47.9607  222.2598 -362.7453  191.1250

E traça o seguinte gráfico -

O MATLAB fornece comandos para trabalhar com transformações, como as transformações de Laplace e Fourier. As transformações são usadas na ciência e na engenharia como uma ferramenta para simplificar a análise e olhar para os dados de outro ângulo.

Por exemplo, a transformada de Fourier nos permite converter um sinal representado em função do tempo em função da frequência. A transformada de Laplace nos permite converter uma equação diferencial em uma equação algébrica.

MATLAB fornece o laplace, fourier e fft comandos para trabalhar com as transformações de Laplace, Fourier e Fast Fourier.

A transformação de Laplace

A transformada de Laplace de uma função de tempo f (t) é dada pela seguinte integral -

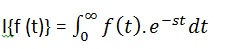
A transformada de Laplace também é denotada como transformada de f (t) em F (s). Você pode ver que esse processo de transformação ou integração converte f (t), uma função da variável simbólica t, em outra função F (s), com outra variável s.

A transformada de Laplace transforma equações diferenciais em algébricas. Para calcular uma transformada de Laplace de uma função f (t), escreva -

laplace(f(t))

Exemplo

Neste exemplo, calcularemos a transformada de Laplace de algumas funções comumente usadas.

Crie um arquivo de script e digite o seguinte código -

syms s t a b w

laplace(a)
laplace(t^2)
laplace(t^9)
laplace(exp(-b*t))
laplace(sin(w*t))
laplace(cos(w*t))

Quando você executa o arquivo, ele exibe o seguinte resultado -

ans =
   1/s^2

ans =
   2/s^3

ans =
   362880/s^10

ans =
   1/(b + s)
  
ans =
   w/(s^2 + w^2)
  
ans =
   s/(s^2 + w^2)

A Transformada Inversa de Laplace

O MATLAB nos permite calcular a transformação inversa de Laplace usando o comando ilaplace.

Por exemplo,

ilaplace(1/s^3)

O MATLAB executará a instrução acima e exibirá o resultado -

ans =
   t^2/2

Exemplo

Crie um arquivo de script e digite o seguinte código -

syms s t a b w

ilaplace(1/s^7)
ilaplace(2/(w+s))
ilaplace(s/(s^2+4))
ilaplace(exp(-b*t))
ilaplace(w/(s^2 + w^2))
ilaplace(s/(s^2 + w^2))

Quando você executa o arquivo, ele exibe o seguinte resultado -

ans =
   t^6/720

ans =
   2*exp(-t*w)

ans =
   cos(2*t)

ans =
   ilaplace(exp(-b*t), t, x)

ans =
   sin(t*w)

ans =
   cos(t*w)

As transformadas de Fourier

As transformadas de Fourier comumente transformam uma função matemática do tempo, f (t), em uma nova função, às vezes denotada por ou F, cujo argumento é frequência com unidades de ciclos / s (hertz) ou radianos por segundo. A nova função é então conhecida como transformada de Fourier e / ou espectro de frequência da função f.

Exemplo

Crie um arquivo de script e digite o seguinte código nele -

syms x 
f = exp(-2*x^2);     %our function
ezplot(f,[-2,2])     % plot of our function
FT = fourier(f)      % Fourier transform

Quando você executa o arquivo, o MATLAB traça o seguinte gráfico -

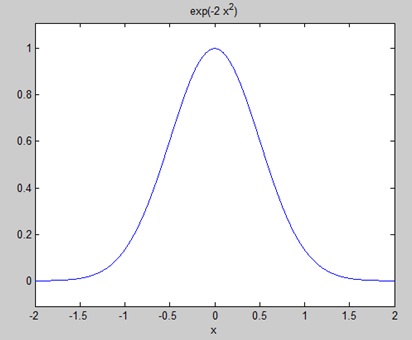
O seguinte resultado é exibido -

FT =
   (2^(1/2)*pi^(1/2)*exp(-w^2/8))/2

Traçando a transformada de Fourier como -

ezplot(FT)

Dá o seguinte gráfico -

Transformadas inversas de Fourier

MATLAB fornece o ifouriercomando para calcular a transformada de Fourier inversa de uma função. Por exemplo,

f = ifourier(-2*exp(-abs(w)))

O MATLAB executará a instrução acima e exibirá o resultado -

f =
   -2/(pi*(x^2 + 1))

GNU Octave é uma linguagem de programação de alto nível como MATLAB e é principalmente compatível com MATLAB. Ele também é usado para cálculos numéricos.

Octave tem as seguintes características comuns com MATLAB -

matrizes são tipos de dados fundamentais
tem suporte integrado para números complexos
tem funções matemáticas e bibliotecas integradas
ele suporta funções definidas pelo usuário

O GNU Octave também é um software livremente redistribuível. Você pode redistribuí-lo e / ou modificá-lo sob os termos da GNU General Public License (GPL), conforme publicada pela Free Software Foundation.

MATLAB vs Octave

A maioria dos programas do MATLAB são executados no Octave, mas alguns dos programas do Octave podem não ser executados no MATLAB porque o Octave permite alguma sintaxe que o MATLAB não permite.

Por exemplo, MATLAB suporta apenas aspas simples, mas Octave suporta aspas simples e duplas para definir strings. Se você está procurando um tutorial sobre o Octave, por favor, siga este tutorial desde o início, que cobre tanto o MATLAB quanto o Octave.

Exemplos Compatíveis

Quase todos os exemplos cobertos neste tutorial são compatíveis com MATLAB e também com Octave. Vamos tentar o seguinte exemplo em MATLAB e Octave que produz o mesmo resultado sem quaisquer alterações de sintaxe -

Este exemplo cria um mapa de superfície 3D para a função g = xe ^{- (x ² + y ² )} . Crie um arquivo de script e digite o seguinte código -

[x,y] = meshgrid(-2:.2:2);
g = x .* exp(-x.^2 - y.^2);
surf(x, y, g)
print -deps graph.eps

Quando você executa o arquivo, o MATLAB exibe o seguinte mapa 3-D -

Exemplos não compatíveis

Embora todas as funcionalidades principais do MATLAB estejam disponíveis no Octave, existem algumas funcionalidades, por exemplo, Cálculo diferencial e de integração, que não correspondem exatamente em ambos os idiomas. Este tutorial tentou fornecer os dois tipos de exemplos em que eles diferiam em sua sintaxe.

Considere o seguinte exemplo em que MATLAB e Octave usam funções diferentes para obter a área de uma curva: f (x) = x ² cos (x) para −4 ≤ x ≤ 9. A seguir está a versão MATLAB do código -

f = x^2*cos(x);
ezplot(f, [-4,9])
a = int(f, -4, 9)
disp('Area: '), disp(double(a));

Quando você executa o arquivo, o MATLAB traça o gráfico -

O seguinte resultado é exibido

a =
8*cos(4) + 18*cos(9) + 14*sin(4) + 79*sin(9)
 
Area: 
   0.3326

Mas para dar área da mesma curva no Octave, você terá que fazer uso de symbolic pacote da seguinte forma -

pkg load symbolic
symbols

x = sym("x");
f = inline("x^2*cos(x)");

ezplot(f, [-4,9])
print -deps graph.eps

[a, ierror, nfneval] = quad(f, -4, 9);
display('Area: '), disp(double(a));

Simulink é um ambiente de simulação e design baseado em modelo para sistemas dinâmicos e embarcados, integrado ao MATLAB. Simulink, também desenvolvido pela MathWorks, é uma ferramenta de linguagem de programação gráfica de fluxo de dados para modelar, simular e analisar sistemas dinâmicos de múltiplos domínios. É basicamente uma ferramenta gráfica de diagramação de blocos com conjunto personalizável de bibliotecas de blocos.

Ele permite que você incorpore algoritmos do MATLAB aos modelos, bem como exporte os resultados da simulação para o MATLAB para análise posterior.

Suporta Simulink -

design de nível de sistema
simulation
geração automática de código
teste e verificação de sistemas embarcados

Existem vários outros produtos complementares fornecidos pela MathWorks e produtos de hardware e software de terceiros que estão disponíveis para uso com o Simulink.

A lista a seguir fornece uma breve descrição de alguns deles -

Stateflow permite o desenvolvimento de máquinas de estado e fluxogramas.
Simulink Coder permite a geração de código-fonte C para implementação em tempo real de sistemas automaticamente.
xPC Target junto com x86-based real-time systems fornecer um ambiente para simular e testar modelos Simulink e Stateflow em tempo real no sistema físico.
Embedded Coder suporta destinos incorporados específicos.
HDL Coder permite gerar automaticamente VHDL e Verilog sintetizáveis.
SimEvents fornece uma biblioteca de blocos de construção gráficos para modelar sistemas de enfileiramento.

O Simulink é capaz de verificação e validação sistemática de modelos por meio de verificação de estilo de modelagem, rastreabilidade de requisitos e análise de cobertura de modelo.

O Simulink Design Verifier permite identificar erros de design e gerar cenários de caso de teste para verificação de modelo.

Usando Simulink

Para abrir o Simulink, digite no espaço de trabalho do MATLAB -

simulink

Simulink abre com o Library Browser. O navegador da biblioteca é usado para construir modelos de simulação.

No painel da janela do lado esquerdo, você encontrará várias bibliotecas categorizadas com base em vários sistemas, clicando em cada uma exibirá os blocos de design no painel da janela à direita.

Modelos de construção

Para criar um novo modelo, clique no Newbotão na barra de ferramentas do navegador da biblioteca. Isso abre uma nova janela de modelo sem título.

Um modelo Simulink é um diagrama de blocos.

Os elementos do modelo são adicionados selecionando os elementos apropriados no Navegador da biblioteca e arrastando-os para a janela Modelo.

Como alternativa, você pode copiar os elementos do modelo e colá-los na janela do modelo.

Exemplos

Arraste e solte itens da biblioteca Simulink para fazer seu projeto.

Para o propósito deste exemplo, dois blocos serão usados para a simulação - A Source (um sinal) e um Sink(um escopo). Um gerador de sinal (a fonte) gera um sinal analógico, que será então visualizado graficamente pelo osciloscópio (o coletor).

Comece arrastando os blocos necessários da biblioteca para a janela do projeto. Em seguida, conecte os blocos, o que pode ser feito arrastando os conectores dos pontos de conexão em um bloco para os de outro.

Vamos arrastar um bloco de 'onda senoidal' para o modelo.