Engenharia de microondas - Dispositivos de microondas

Assim como outros sistemas, os sistemas de micro-ondas consistem em muitos componentes de micro-ondas, principalmente com fonte em uma extremidade e carga na outra, todos conectados com guias de ondas ou cabos coaxiais ou sistemas de linha de transmissão.

A seguir estão as propriedades dos guias de ondas.

• SNR alto
• Baixa atenuação
• Perda de inserção inferior

Funções Waveguide Microondas

Considere um guia de ondas com 4 portas. Se a energia for aplicada a uma porta, ela passa por todas as 3 portas em algumas proporções onde parte dela pode refletir de volta na mesma porta. Este conceito é claramente representado na figura a seguir.

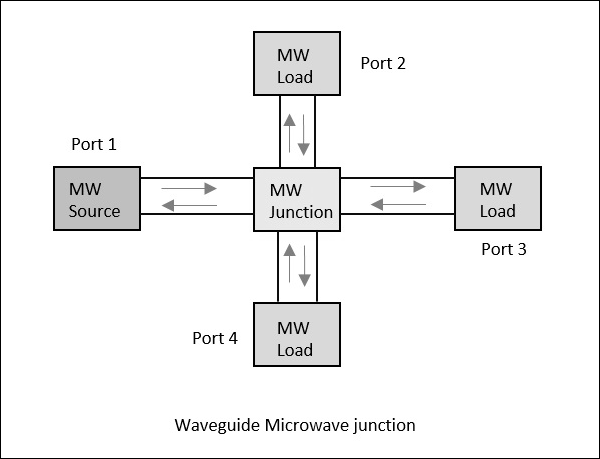
Parâmetros de dispersão

Para uma rede de duas portas, conforme mostrado na figura a seguir, se a energia for aplicada em uma porta, como acabamos de discutir, a maior parte da energia escapa da outra porta, enquanto parte dela reflete de volta para a mesma porta. Na figura a seguir, seV₁ ou V₂ é aplicado, então I₁ ou I₂ corrente flui respectivamente.

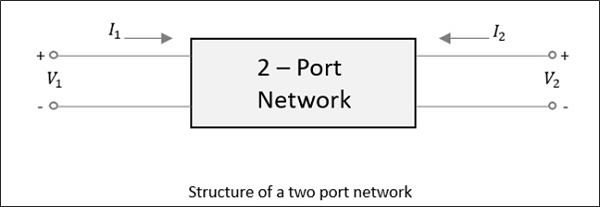
Se a fonte for aplicada à porta oposta, outras duas combinações devem ser consideradas. Portanto, para uma rede de duas portas, 2 × 2 = 4 combinações são prováveis ​​de ocorrer.

As ondas viajantes com potências associadas quando se espalham pelas portas, a junção de microondas pode ser definida por parâmetros S ou Scattering Parameters, que são representados em uma forma de matriz, chamados de "Scattering Matrix"

Matriz de Dispersão

É uma matriz quadrada que fornece todas as combinações de relações de energia entre as várias portas de entrada e saída de uma junção de micro-ondas. Os elementos desta matriz são chamados"Scattering Coefficients" ou "Scattering (S) Parameters".

Considere a seguinte figura.

Aqui, a fonte está conectada através da linha $ i ^ {th} $, enquanto $ a_1 $ é a onda incidente e $ b_1 $ é a onda refletida.

Se uma relação é dada entre $ b_1 $ e $ a_1 $,

$$ b_1 = (reflexo \: \: coeficiente) a_1 = S_ {1i} a_1 $$

Onde

• $ S_ {1i} $ = Coeficiente de reflexão de $ 1 ^ {st} $ linha (onde $ i $ é a porta de entrada e $ 1 $ é a porta de saída)

• $ 1 $ = Reflexo da linha $ 1 ^ {st} $

• $ i $ = Fonte conectada em $ i ^ {th} $ linha

Se a impedância for compatível, a energia será transferida para a carga. Improvável, se a impedância da carga não corresponder à impedância característica. Então, ocorre a reflexão. Isso significa que a reflexão ocorre se

$$ Z_l \ neq Z_o $$

No entanto, se essa incompatibilidade existe para mais de uma porta, por exemplo $ 'n' $ portas, então $ i = 1 $ a $ n $ (uma vez que $ i $ pode ser qualquer linha de $ 1 $ a $ n $).

Portanto, temos

$$ b_1 = S_ {11} a_1 + S_ {12} a_2 + S_ {13} a_3 + ............... + S_ {1n} a_n $$

$$ b_2 = S_ {21} a_1 + S_ {22} a_2 + S_ {23} a_3 + ............... + S_ {2n} a_n $$

$$. $$

$$. $$

$$. $$

$$. $$

$$. $$

$$ b_n = S_ {n1} a_1 + S_ {n2} a_2 + S_ {n3} a_3 + ............... + S_ {nn} a_n $$

Quando tudo isso é mantido em forma de matriz,

$$ \ begin {bmatrix} b_1 \\ b_2 \\ b_3 \\. \\. \\. \\ b_n \ end {bmatrix} = \ begin {bmatrix} S_ {11} & S_ {12} & S_ {13 } & ... & S_ {1n} \\ S_ {21} & S_ {22} & S_ {23} & ... & S_ {2n} \\. &. &. & ... &. \\. &. &. & ... &. \\. &. &. & ... &. \\ S_ {n1} & S_ {n2} & S_ {n3} & ... & S_ {nn} \\ \ end {bmatrix} \ times \ begin {bmatrix} a_1 \\ a_2 \\ a_3 \\. \ \. \\. \\ a_n \ end {bmatrix} $$

Column matrix $ [b] $ Scattering matrix $ [S] $Matrix $ [a] $

A matriz da coluna $ \ left [b \ right] $ corresponde às ondas refletidas ou à saída, enquanto a matriz $ \ left [a \ right] $ corresponde às ondas incidentes ou à entrada. A matriz da coluna de dispersão $ \ left [s \ right] $ que é da ordem de $ n \ vezes n $ contém os coeficientes de reflexão e os coeficientes de transmissão. Portanto,

$$ \ esquerda [b \ direita] = \ esquerda [S \ direita] \ esquerda [a \ direita] $$

Propriedades da [S] Matrix

A matriz de dispersão é indicada como matriz $ [S] $. Existem algumas propriedades padrão para a matriz $ [S] $. Eles são -

• $ [S] $ é sempre uma matriz quadrada de ordem (nxn)

  $ [S] _ {n \ vezes n} $

• $ [S] $ é uma matriz simétrica

  ou seja, $ S_ {ij} = S_ {ji} $

• $ [S] $ é uma matriz unitária

  ou seja, $ [S] [S] ^ * = I $

• A soma dos produtos de cada termo de qualquer linha ou coluna multiplicado pelo conjugado complexo dos termos correspondentes de qualquer outra linha ou coluna é zero. ie,

$$ \ sum_ {i = j} ^ {n} S_ {ik} S_ {ik} ^ {*} = 0 \: para \: k \ neq j $$

$$ (k = 1,2,3, ... \: n) \: e \: (j = 1,2,3, ... \: n) $$

• Se a distância elétrica entre algum porto $ k ^ {th} $ e a junção for $ \ beta _kI_k $, então os coeficientes de $ S_ {ij} $ envolvendo $ k $ serão multiplicados pelo fator $ e ^ {- j \ beta kIk} $

Nos próximos capítulos, daremos uma olhada nos diferentes tipos de junções em T de Microondas.