TensorFlow - Fundamentos matemáticos

É importante entender os conceitos matemáticos necessários para o TensorFlow antes de criar o aplicativo básico no TensorFlow. A matemática é considerada o coração de qualquer algoritmo de aprendizado de máquina. É com a ajuda de conceitos centrais da Matemática, uma solução para um algoritmo específico de aprendizado de máquina é definida.

Vetor

Uma matriz de números, que é contínua ou discreta, é definida como um vetor. Algoritmos de aprendizado de máquina lidam com vetores de comprimento fixo para melhor geração de saída.

Os algoritmos de aprendizado de máquina lidam com dados multidimensionais, de modo que os vetores desempenham um papel crucial.

A representação pictórica do modelo vetorial é mostrada abaixo -

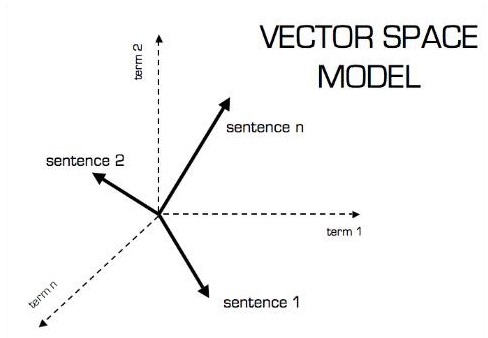
Escalar

O escalar pode ser definido como um vetor unidimensional. Escalares são aqueles que incluem apenas magnitude e nenhuma direção. Com escalares, estamos preocupados apenas com a magnitude.

Exemplos de escalares incluem parâmetros de peso e altura de crianças.

Matriz

Matrix pode ser definida como arrays multidimensionais, que são organizados no formato de linhas e colunas. O tamanho da matriz é definido pelo comprimento da linha e comprimento da coluna. A figura a seguir mostra a representação de qualquer matriz especificada.

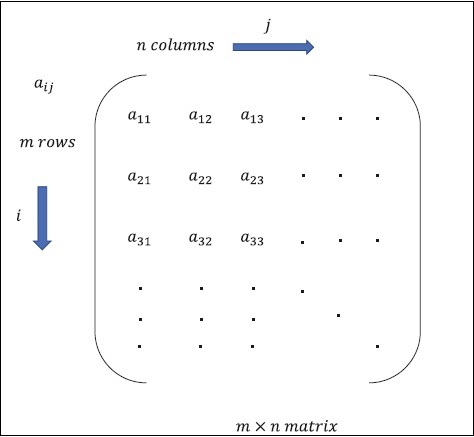
Considere a matriz com “m” linhas e “n” colunas como mencionado acima, a representação da matriz será especificada como “m * n matriz” que definiu o comprimento da matriz também.

Computações Matemáticas

Nesta seção, aprenderemos sobre os diferentes cálculos matemáticos no TensorFlow.

Adição de matrizes

A adição de duas ou mais matrizes é possível se as matrizes forem da mesma dimensão. A adição implica a adição de cada elemento de acordo com a posição dada.

Considere o exemplo a seguir para entender como a adição de matrizes funciona -

$$ Exemplo: A = \ begin {bmatrix} 1 e 2 \\ 3 & 4 \ end {bmatrix} B = \ begin {bmatrix} 5 e 6 \\ 7 & 8 \ end {bmatrix} \: então \: A + B = \ begin {bmatrix} 1 + 5 & 2 + 6 \\ 3 + 7 & 4 + 8 \ end {bmatrix} = \ begin {bmatrix} 6 e 8 \\ 10 & 12 \ end {bmatrix} $$

Subtração de matrizes

A subtração de matrizes opera de maneira semelhante, como a adição de duas matrizes. O usuário pode subtrair duas matrizes, desde que as dimensões sejam iguais.

$$ Exemplo: A- \ begin {bmatrix} 1 e 2 \\ 3 & 4 \ end {bmatrix} B- \ begin {bmatrix} 5 e 6 \\ 7 & 8 \ end {bmatrix} \: então \: AB - \ begin {bmatrix} 1-5 e 2-6 \\ 3-7 & 4-8 \ end {bmatrix} - \ begin {bmatrix} -4 e -4 \\ - 4 e -4 \ end {bmatrix} $$

Multiplicação de matrizes

Para que duas matrizes A m * n e B p * q sejam multiplicáveis, n deve ser igual a p. A matriz resultante é -

C m * q

$$ A = \ begin {bmatrix} 1 e 2 \\ 3 & 4 \ end {bmatrix} B = \ begin {bmatrix} 5 e 6 \\ 7 e 8 \ end {bmatrix} $$

$$ c_ {11} = \ begin {bmatrix} 1 e 2 \ end {bmatrix} \ begin {bmatrix} 5 \\ 7 \ end {bmatrix} = 1 \ times5 + 2 \ times7 = 19 \: c_ {12} = \ begin {bmatrix} 1 e 2 \ end {bmatrix} \ begin {bmatrix} 6 \\ 8 \ end {bmatrix} = 1 \ times6 + 2 \ times8 = 22 $$

$$ c_ {21} = \ begin {bmatrix} 3 & 4 \ end {bmatrix} \ begin {bmatrix} 5 \\ 7 \ end {bmatrix} = 3 \ times5 + 4 \ times7 = 43 \: c_ {22} = \ begin {bmatrix} 3 e 4 \ end {bmatrix} \ begin {bmatrix} 6 \\ 8 \ end {bmatrix} = 3 \ times6 + 4 \ times8 = 50 $$

$$ C = \ begin {bmatrix} c_ {11} & c_ {12} \\ c_ {21} & c_ {22} \ end {bmatrix} = \ begin {bmatrix} 19 e 22 \\ 43 & 50 \ end {bmatrix} $$

Transpor da matriz

A transposta de uma matriz A, m * n é geralmente representada por AT (transposta) n * m e é obtida pela transposição dos vetores coluna como vetores linha.

$$ Exemplo: A = \ begin {bmatrix} 1 & 2 \\ 3 & 4 \ end {bmatrix} \: então \: A ^ {T} \ begin {bmatrix} 1 & 3 \\ 2 & 4 \ end { bmatrix} $$

Produto escalar de vetores

Qualquer vetor de dimensão n pode ser representado como uma matriz v = R ^ n * 1.

$$ v_ {1} = \ begin {bmatrix} v_ {11} \\ v_ {12} \\\ cdot \\\ cdot \\\ cdot \\ v_ {1n} \ end {bmatrix} v_ {2} = \ begin {bmatrix} v_ {21} \\ v_ {22} \\\ cdot \\\ cdot \\\ cdot \\ v_ {2n} \ end {bmatrix} $$

O produto escalar de dois vetores é a soma do produto dos componentes correspondentes - Componentes ao longo da mesma dimensão e podem ser expressos como

$$ v_ {1} \ cdot v_ {2} = v_1 ^ Tv_ {2} = v_2 ^ Tv_ {1} = v_ {11} v_ {21} + v_ {12} v_ {22} + \ cdot \ cdot + v_ {1n} v_ {2n} = \ displaystyle \ sum \ limits_ {k = 1} ^ n v_ {1k} v_ {2k} $$

O exemplo de produto escalar de vetores é mencionado abaixo -

$$ Exemplo: v_ {1} = \ begin {bmatrix} 1 \\ 2 \\ 3 \ end {bmatrix} v_ {2} = \ begin {bmatrix} 3 \\ 5 \\ - 1 \ end {bmatrix} v_ {1} \ cdot v_ {2} = v_1 ^ Tv_ {2} = 1 \ times3 + 2 \ times5-3 \ times1 = 10 $$