Самоорганизующиеся карты функций Кохонена
Предположим, у нас есть какой-то паттерн произвольных размеров, однако они нам нужны в одном или двух измерениях. Тогда процесс сопоставления признаков будет очень полезен для преобразования широкого пространства шаблонов в типичное пространство признаков. Теперь возникает вопрос, почему нам нужна самоорганизующаяся карта функций? Причина в том, что помимо возможности преобразования произвольных размеров в 1-D или 2-D, он также должен иметь возможность сохранять топологию соседей.
Топологии соседей в Kohonen SOM
Могут быть разные топологии, но чаще всего используются следующие две топологии:
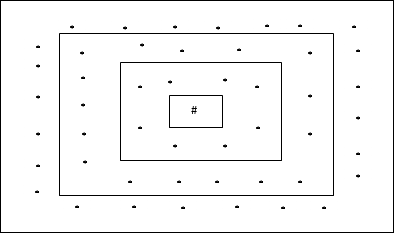
Топология прямоугольной сетки
Эта топология имеет 24 узла в сетке расстояния-2, 16 узлов в сетке расстояния-1 и 8 узлов в сетке расстояния-0, что означает, что разница между каждой прямоугольной сеткой составляет 8 узлов. Победившая единица обозначена #.
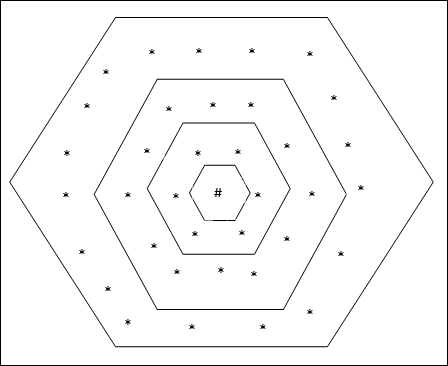
Топология гексагональной сетки
Эта топология имеет 18 узлов в сетке расстояния-2, 12 узлов в сетке расстояния-1 и 6 узлов в сетке расстояния-0, что означает, что разница между каждой прямоугольной сеткой составляет 6 узлов. Победившая единица обозначена #.
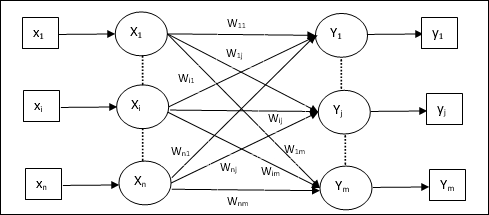
Архитектура
Архитектура KSOM аналогична архитектуре конкурентной сети. С помощью схем соседства, обсужденных ранее, обучение может происходить в расширенной области сети.
Алгоритм обучения
Step 1 - Инициализировать веса, скорость обучения α и топологическая схема окрестности.
Step 2 - Продолжайте шаги 3-9, если условие остановки не выполняется.
Step 3 - Продолжайте шаги 4-6 для каждого входного вектора x.
Step 4 - Вычислить квадрат евклидова расстояния для j = 1 to m
$$ D (j) \: = \: \ displaystyle \ sum \ limits_ {i = 1} ^ n \ displaystyle \ sum \ limits_ {j = 1} ^ m (x_ {i} \: - \: w_ {ij) }) ^ 2 $$
Step 5 - Получить победный отряд J где D(j) минимально.
Step 6 - Рассчитайте новый вес выигрышной единицы по следующей формуле -
$$ w_ {ij} (новый) \: = \: w_ {ij} (старый) \: + \: \ alpha [x_ {i} \: - \: w_ {ij} (старый)] $$
Step 7 - Обновить скорость обучения α следующим соотношением -
$$ \ alpha (t \: + \: 1) \: = \: 0.5 \ alpha t $$
Step 8 - Уменьшить радиус топологической схемы.
Step 9 - Проверьте состояние остановки сети.