Искусственная нейронная сеть - Краткое руководство

Нейронные сети - это параллельные вычислительные устройства, которые, по сути, представляют собой попытку создать компьютерную модель мозга. Основная цель - разработать систему для выполнения различных вычислительных задач быстрее, чем традиционные системы. Эти задачи включают распознавание и классификацию образов, аппроксимацию, оптимизацию и кластеризацию данных.

Что такое искусственная нейронная сеть?

Искусственная нейронная сеть (ИНС) - это эффективная вычислительная система, центральная тема которой заимствована из аналогии с биологическими нейронными сетями. ИНС также называют «искусственными нейронными системами», «системами параллельной распределенной обработки» или «системами коннекционизма». ИНС получает большой набор блоков, которые связаны между собой по некоторому шаблону, чтобы обеспечить связь между блоками. Эти блоки, также называемые узлами или нейронами, представляют собой простые процессоры, которые работают параллельно.

Каждый нейрон связан с другим нейроном через соединение. Каждая ссылка для подключения связана с весом, который содержит информацию о входном сигнале. Это наиболее полезная информация для нейронов при решении конкретной проблемы, поскольку вес обычно возбуждает или подавляет передаваемый сигнал. Каждый нейрон имеет внутреннее состояние, которое называется сигналом активации. Выходные сигналы, которые создаются после объединения входных сигналов и правила активации, могут быть отправлены на другие устройства.

Краткая история ИНС

Историю ИНС можно разделить на следующие три эпохи:

ИНС 1940-1960-х гг.

Вот некоторые ключевые события этой эпохи:

• 1943 - Предполагалось, что концепция нейронной сети началась с работы физиолога Уоррена МакКаллока и математика Уолтера Питтса, когда в 1943 году они смоделировали простую нейронную сеть с использованием электрических цепей, чтобы описать, как могут работать нейроны в мозге. .

• 1949- В книге Дональда Хебба « Организация поведения» утверждается, что повторная активация одного нейрона другим увеличивает его силу каждый раз, когда они используются.

• 1956 - Ассоциативная сеть памяти была представлена ​​Тейлором.

• 1958 - Метод обучения нейронной модели Мак-Каллока и Питтса под названием Perceptron был изобретен Розенблаттом.

• 1960 - Бернард Видроу и Марсиан Хофф разработали модели под названием «АДАЛИН» и «МАДАЛИН».

ИНС в 1960-1980-х гг.

Вот некоторые ключевые события этой эпохи:

• 1961 - Розенблатт предпринял неудачную попытку, но предложил схему «обратного распространения» для многоуровневых сетей.

• 1964 - Тейлор построил схему «победитель получает все» с запретами среди выходных устройств.

• 1969 - Многослойный перцептрон (MLP) был изобретен Мински и Паперт.

• 1971 - У Кохонена развилась ассоциативная память.

• 1976 - Стивен Гроссберг и Гейл Карпентер разработали теорию адаптивного резонанса.

ИНС с 1980-х годов по настоящее время

Вот некоторые ключевые события этой эпохи:

• 1982 - Основным событием стал энергетический подход Хопфилда.

• 1985 - Машина Больцмана была разработана Экли, Хинтоном и Сейновски.

• 1986 - Рамелхарт, Хинтон и Уильямс ввели обобщенное правило дельты.

• 1988 - Коско разработал двоичную ассоциативную память (BAM), а также дал концепцию нечеткой логики в ИНС.

Исторический обзор показывает, что в этой области достигнут значительный прогресс. Появляются микросхемы на основе нейронных сетей, и разрабатываются приложения для решения сложных задач. Несомненно, сегодня переходный период для нейросетевых технологий.

Биологический нейрон

Нервная клетка (нейрон) - это особая биологическая клетка, обрабатывающая информацию. По оценке, существует огромное количество нейронов, примерно 10 ¹¹ с многочисленными взаимосвязями, примерно 10 ¹⁵ .

Схематическая диаграмма

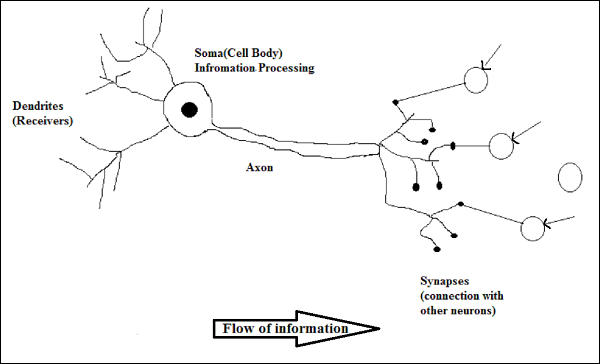
Работа биологического нейрона

Как показано на приведенной выше диаграмме, типичный нейрон состоит из следующих четырех частей, с помощью которых мы можем объяснить его работу:

• Dendrites- Это древовидные ветви, отвечающие за получение информации от других нейронов, с которыми они связаны. В другом смысле можно сказать, что они похожи на уши нейрона.

• Soma - Это тело клетки нейрона и отвечает за обработку информации, полученной от дендритов.

• Axon - Это как кабель, по которому нейроны отправляют информацию.

• Synapses - Это связь между аксоном и дендритами других нейронов.

ANN против BNN

Прежде чем взглянуть на различия между искусственной нейронной сетью (ИНС) и биологической нейронной сетью (BNN), давайте посмотрим на сходства, основанные на терминологии между этими двумя.

Биологическая нейронная сеть (BNN)	Искусственная нейронная сеть (ИНС)
Сома	Узел
Дендриты	Ввод
Синапс	Вес или соединения
Аксон	Вывод

В следующей таблице показано сравнение ИНС и BNN на основе некоторых упомянутых критериев.

Критерии	BNN	ЭНН
Processing	Массивно параллельный, медленный, но лучше, чем ИНС	Массивно параллельные, быстрые, но уступающие BNN
Size	10 11 нейронов и 10 15 взаимосвязей	От 10 2 до 10 4 узлов (в основном зависит от типа приложения и разработчика сети)
Learning	Они могут терпеть двусмысленность	Требуются очень точные, структурированные и отформатированные данные, чтобы допустить двусмысленность
Fault tolerance	Производительность ухудшается даже при частичном повреждении	Он обладает высокой производительностью и, следовательно, может быть отказоустойчивым.
Storage capacity	Хранит информацию в синапсе	Сохраняет информацию в постоянных ячейках памяти

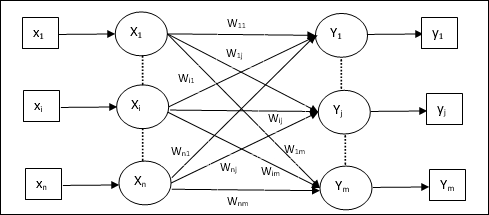
Модель искусственной нейронной сети

На следующей диаграмме представлена ​​общая модель ИНС с последующей ее обработкой.

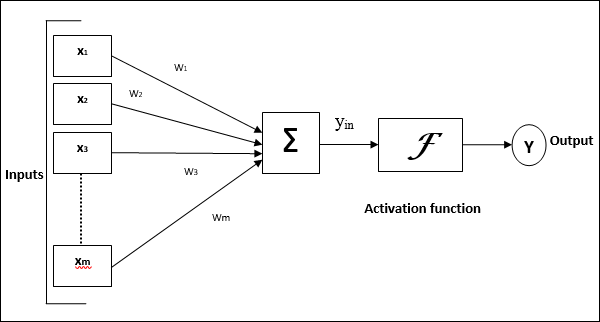
Для приведенной выше общей модели искусственной нейронной сети чистый вход можно рассчитать следующим образом:

$$ y_ {in} \: = \: x_ {1} .w_ {1} \: + \: x_ {2} .w_ {2} \: + \: x_ {3} .w_ {3} \: \ dotso \: x_ {m} .w_ {m} $$

т.е. чистый ввод $ y_ {in} \: = \: \ sum_i ^ m \: x_ {i} .w_ {i} $

Выход можно рассчитать, применив функцию активации к входу сети.

$$ Y \: = \: F (y_ {in}) $$

Выход = функция (чистый вход рассчитан)

Обработка ИНС зависит от следующих трех строительных блоков:

• Топология сети
• Регулировка веса или обучение
• Функции активации

В этой главе мы подробно обсудим эти три строительных блока ИНС.

Топология сети

Топология сети - это расположение сети вместе с ее узлами и соединительными линиями. По топологии ИНС можно разделить на следующие виды:

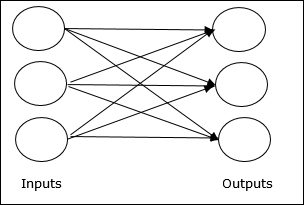
Прямая связь

Это непериодическая сеть, имеющая блоки обработки / узлы на уровнях, и все узлы на уровне связаны с узлами предыдущих уровней. Связь имеет разный вес. Отсутствие обратной связи означает, что сигнал может течь только в одном направлении, от входа к выходу. Его можно разделить на следующие два типа:

• Single layer feedforward network- Концепция состоит в том, что ИНС прямого распространения имеет только один взвешенный уровень. Другими словами, мы можем сказать, что входной слой полностью связан с выходным слоем.

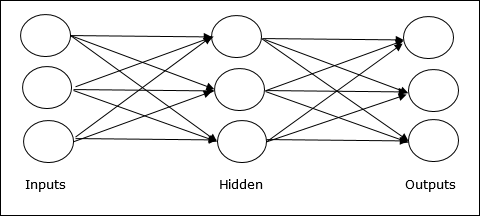
• Multilayer feedforward network- Концепция состоит в том, что ИНС прямого распространения имеет более одного взвешенного уровня. Поскольку эта сеть имеет один или несколько слоев между входным и выходным слоями, она называется скрытыми слоями.

Сеть обратной связи

Как следует из названия, сеть обратной связи имеет пути обратной связи, что означает, что сигнал может течь в обоих направлениях с использованием петель. Это делает его нелинейной динамической системой, которая постоянно изменяется, пока не достигнет состояния равновесия. Его можно разделить на следующие типы -

• Recurrent networks- Это сети обратной связи с замкнутыми контурами. Ниже приведены два типа повторяющихся сетей.

• Fully recurrent network - Это простейшая архитектура нейронной сети, потому что все узлы подключены ко всем остальным узлам, и каждый узел работает как на входе, так и на выходе.

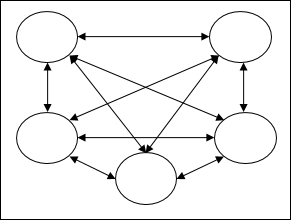
• Jordan network - Это сеть с замкнутым контуром, в которой выход снова будет поступать на вход в качестве обратной связи, как показано на следующей диаграмме.

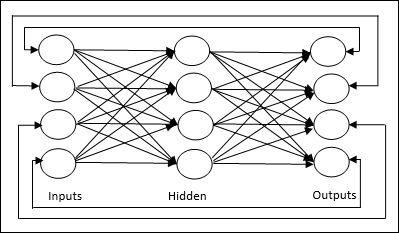
Регулировка веса или обучение

Обучение в искусственной нейронной сети - это метод изменения весов связей между нейронами указанной сети. Обучение в ИНС можно разделить на три категории: обучение с учителем, обучение без учителя и обучение с подкреплением.

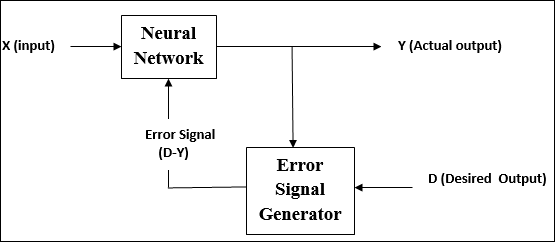
Контролируемое обучение

Как следует из названия, этот тип обучения проводится под руководством учителя. Этот процесс обучения зависим.

Во время обучения ИНС при обучении с учителем входной вектор представляется сети, которая дает выходной вектор. Этот выходной вектор сравнивается с желаемым выходным вектором. Сигнал ошибки генерируется, если есть разница между фактическим выходным сигналом и желаемым выходным вектором. На основе этого сигнала ошибки веса корректируются до тех пор, пока фактический выход не совпадет с желаемым выходом.

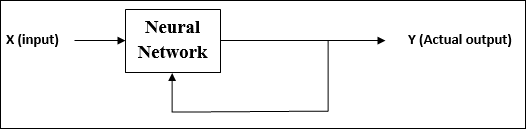
Неконтролируемое обучение

Как следует из названия, этот тип обучения осуществляется без присмотра учителя. Этот процесс обучения независим.

Во время обучения ИНС в условиях обучения без учителя входные векторы одного типа объединяются в кластеры. Когда применяется новый шаблон ввода, нейронная сеть выдает выходной ответ, указывающий класс, к которому принадлежит шаблон ввода.

Из среды нет обратной связи относительно того, каким должен быть желаемый результат, и является ли он правильным или неправильным. Следовательно, в этом типе обучения сама сеть должна обнаруживать закономерности и особенности входных данных и соотношение входных данных с выходными.

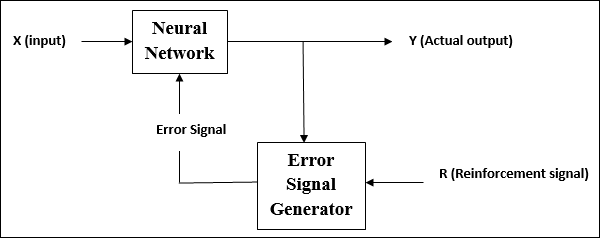
Обучение с подкреплением

Как следует из названия, этот тип обучения используется для усиления или усиления сети через некоторую критическую информацию. Этот процесс обучения похож на обучение с учителем, однако у нас может быть очень мало информации.

Во время обучения сети в рамках обучения с подкреплением сеть получает некоторую обратную связь от окружающей среды. Это делает его несколько похожим на обучение с учителем. Однако полученная здесь обратная связь является оценочной, а не поучительной, что означает, что здесь нет учителя, как при обучении с учителем. После получения обратной связи сеть выполняет корректировку весов, чтобы в будущем получать более точную информацию о критике.

Функции активации

Это может быть определено как дополнительная сила или усилие, приложенное к входу для получения точного выхода. В ИНС мы также можем применять функции активации ко входу, чтобы получить точный результат. Ниже приведены некоторые интересующие функции активации -

Функция линейной активации

Ее также называют функцией идентификации, поскольку она не выполняет редактирование ввода. Это можно определить как -

$$ F (x) \: = \: x $$

Функция активации сигмовидной кишки

Он бывает двух типов:

• Binary sigmoidal function- Эта функция активации выполняет редактирование ввода от 0 до 1. Это положительный характер. Он всегда ограничен, что означает, что его выход не может быть меньше 0 и больше 1. Он также строго возрастает по своей природе, что означает, что чем больше вход выше, тем выходом. Его можно определить как

  $$ F (x) \: = \: sigm (x) \: = \: \ frac {1} {1 \: + \: exp (-x)} $$

• Bipolar sigmoidal function- Эта функция активации выполняет редактирование ввода от -1 до 1. Он может быть положительным или отрицательным по своей природе. Он всегда ограничен, что означает, что его выход не может быть меньше -1 и больше 1. Он также строго возрастает по своей природе, как сигмовидная функция. Его можно определить как

  $$ F (x) \: = \: sigm (x) \: = \: \ frac {2} {1 \: + \: exp (-x)} \: - \: 1 \: = \: \ гидроразрыв {1 \: - \: exp (x)} {1 \: + \: exp (x)} $$

Как указывалось ранее, ИНС полностью вдохновлена ​​принципом работы биологической нервной системы, то есть человеческого мозга. Самая впечатляющая характеристика человеческого мозга - это способность к обучению, поэтому ИНС приобретает ту же функцию.

Что такое обучение в ИНС?

По сути, обучение означает вносить изменения в себя и адаптировать их к изменениям в окружающей среде. ИНС - это сложная система или, точнее, мы можем сказать, что это сложная адаптивная система, которая может изменять свою внутреннюю структуру на основе информации, проходящей через нее.

Почему это важно?

Будучи сложной адаптивной системой, обучение в ИНС подразумевает, что блок обработки способен изменять свое поведение ввода / вывода из-за изменения окружающей среды. Важность обучения в ИНС возрастает из-за фиксированной функции активации, а также вектора ввода / вывода при построении конкретной сети. Теперь, чтобы изменить поведение ввода / вывода, нам нужно настроить веса.

Классификация

Его можно определить как процесс обучения различению данных выборок по разным классам путем нахождения общих черт между выборками одних и тех же классов. Например, для обучения ИНС у нас есть несколько обучающих выборок с уникальными функциями, а для ее тестирования у нас есть несколько тестовых образцов с другими уникальными функциями. Классификация - это пример обучения с учителем.

Правила обучения нейронной сети

Мы знаем, что во время обучения ИНС, чтобы изменить поведение ввода / вывода, нам нужно настроить веса. Следовательно, требуется метод, с помощью которого можно изменять веса. Эти методы называются правилами обучения, которые представляют собой просто алгоритмы или уравнения. Ниже приведены некоторые правила обучения нейронной сети.

Правило обучения по-еврейски

Это правило, одно из старейших и простейших, было введено Дональдом Хеббом в его книге «Организация поведения» в 1949 году. Это своего рода обучение без учителя с прямой связью.

Basic Concept - Это правило основано на предложении Хебба, который написал:

«Когда аксон клетки A находится достаточно близко, чтобы возбудить клетку B, и неоднократно или постоянно участвует в ее возбуждении, в одной или обеих клетках происходит некоторый процесс роста или метаболические изменения, так что эффективность A, как одной из клеток, запускающих B , увеличена."

Из приведенного выше постулата мы можем сделать вывод, что связи между двумя нейронами могут быть усилены, если нейроны срабатывают одновременно, и могут ослабнуть, если они срабатывают в разное время.

Mathematical Formulation - Согласно правилу обучения Hebbian, следующая формула увеличивает вес соединения на каждом временном шаге.

$$ \ Delta w_ {ji} (t) \: = \: \ alpha x_ {i} (t) .y_ {j} (t) $$

Здесь $ \ Delta w_ {ji} (t) $ ⁡ = приращение, на которое вес соединения увеличивается на временном шаге t

$ \ alpha $ = положительная и постоянная скорость обучения

$ x_ {i} (t) $ = входное значение от пресинаптического нейрона на временном шаге t

$ y_ {i} (t) $ = выход пресинаптического нейрона на том же временном шаге t

Правило обучения персептрона

Это правило является исправлением ошибок алгоритма контролируемого обучения однослойных сетей прямого распространения с линейной функцией активации, введенного Розенблаттом.

Basic Concept- Поскольку по своей природе контролируется, для вычисления ошибки будет проводиться сравнение между желаемым / целевым выходом и фактическим выходом. Если обнаружено какое-либо различие, необходимо изменить веса соединения.

Mathematical Formulation - Чтобы объяснить его математическую формулировку, предположим, что у нас есть n конечных входных векторов x (n), а также его желаемый / целевой выходной вектор t (n), где n = от 1 до N.

Теперь выход 'y' может быть вычислен, как объяснялось ранее, на основе чистого входа, а функция активации, применяемая к этому чистому входу, может быть выражена следующим образом:

$$ y \: = \: f (y_ {in}) \: = \: \ begin {cases} 1, & y_ {in} \:> \: \ theta \\ 0, & y_ {in} \: \ leqslant \: \ theta \ end {case} $$

где θ порог.

Обновление веса может быть выполнено в следующих двух случаях:

Case I - когда t ≠ y, тогда

$$ w (новый) \: = \: w (старый) \: + \; tx $$

Case II - когда t = y, тогда

Без изменения веса

Правило дельта-обучения (правило Уидроу-Хоффа)

Он был введен Бернардом Видроу и Марсианом Хоффом, также называемый методом наименьших средних квадратов (LMS), чтобы минимизировать ошибку по всем шаблонам обучения. Это своего рода контролируемый алгоритм обучения с функцией непрерывной активации.

Basic Concept- В основе этого правила лежит метод градиентного спуска, который продолжается вечно. Правило дельты обновляет синаптические веса, чтобы минимизировать чистый ввод в выходной блок и целевое значение.

Mathematical Formulation - Для обновления синаптических весов дельта-правило задается следующим образом:

$$ \ Delta w_ {i} \: = \: \ alpha \ :. x_ {i} .e_ {j} $$

Здесь $ \ Delta w_ {i} $ = изменение веса для i- ^го ⁡ шаблона;

$ \ alpha $ = положительная и постоянная скорость обучения;

$ x_ {i} $ = входное значение от пресинаптического нейрона;

$ e_ {j} $ = $ (t \: - \: y_ {in}) $, разница между желаемым / целевым выходом и фактическим выходом ⁡ $ y_ {in} $

Приведенное выше правило дельты действует только для одного выходного устройства.

Обновление веса может быть выполнено в следующих двух случаях:

Case-I - когда t ≠ y, тогда

$$ w (новый) \: = \: w (старый) \: + \: \ Delta w $$

Case-II - когда t = y, тогда

Без изменения веса

Правило соревновательного обучения (победитель получает все)

Он связан с обучением без учителя, в котором выходные узлы пытаются конкурировать друг с другом, чтобы представить входной шаблон. Чтобы понять это правило обучения, мы должны понять конкурентную сеть, которая представлена ​​следующим образом:

Basic Concept of Competitive Network- Эта сеть похожа на однослойную сеть с прямой связью с обратной связью между выходами. Связи между выходами являются тормозными, показаны пунктирными линиями, что означает, что конкуренты никогда не поддерживают себя.

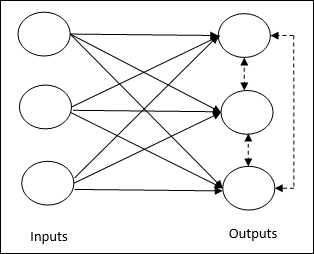
Basic Concept of Competitive Learning Rule- Как было сказано ранее, между выходными узлами будет конкуренция. Следовательно, основная концепция заключается в том, что во время обучения устройство вывода с наибольшей активацией данного шаблона ввода будет объявлено победителем. Это правило также называется принципом «победитель получает все», потому что обновляется только нейрон-победитель, а остальные нейроны остаются неизменными.

Mathematical formulation - Ниже приведены три важных фактора для математической формулировки этого правила обучения.

• Condition to be a winner - Предположим, что если нейрон $ y_ {k} $ ⁡ хочет стать победителем, тогда будет следующее условие -

  $$ y_ {k} \: = \: \ begin {cases} 1 & if \: v_ {k} \:> \: v_ {j} \: for \: all \: j, \: j \: \ neq \: k \\ 0 и иначе \ end {case} $$

Это означает, что если какой-либо нейрон, скажем, $ y_ {k} $ ⁡, хочет выиграть, то его индуцированное локальное поле (выход блока суммирования), скажем $ v_ {k} $, должно быть самым большим среди всех других нейронов. в сети.

• Condition of sum total of weight - Другим ограничением правила конкурентного обучения является то, что сумма весов конкретного выходного нейрона будет равна 1. Например, если мы рассмотрим нейрон k тогда -

  $$ \ displaystyle \ sum \ limits_ {j} w_ {kj} \: = \: 1 \: \: \: \: \: \: \: \: \: для \: all \: k $$

• Change of weight for winner- Если нейрон не реагирует на входной шаблон, то в этом нейроне не происходит обучения. Однако, если побеждает конкретный нейрон, соответствующие веса корректируются следующим образом

  $$ \ Delta w_ {kj} \: = \: \ begin {cases} - \ alpha (x_ {j} \: - \: w_ {kj}), & if \: нейрон \: k \: победит \\ 0, & if \: нейрон \: k \: loss \ end {cases} $$

Здесь $ \ alpha $ - скорость обучения.

Это ясно показывает, что мы отдаем предпочтение победившему нейрону, регулируя его вес, и если происходит потеря нейрона, нам не нужно беспокоиться о корректировке его веса.

Правило обучения Outstar

Это правило, введенное Гроссбергом, касается обучения с учителем, поскольку желаемые результаты известны. Это также называется обучением Гроссберга.

Basic Concept- Это правило применяется к нейронам, расположенным в слой. Он специально разработан для получения желаемого результатаd слоя p нейроны.

Mathematical Formulation - Корректировки веса в этом правиле рассчитываются следующим образом

$$ \ Delta w_ {j} \: = \: \ alpha \ :( d \: - \: w_ {j}) $$

Вот d - желаемый выход нейрона, а $ \ alpha $ - скорость обучения.

Как следует из названия, supervised learningпроходит под присмотром учителя. Этот процесс обучения зависим. Во время обучения ИНС в условиях контролируемого обучения входной вектор представляется сети, которая создает выходной вектор. Этот выходной вектор сравнивается с желаемым / целевым выходным вектором. Сигнал ошибки генерируется, если есть разница между фактическим выходным сигналом и желаемым / целевым вектором выходного сигнала. На основе этого сигнала ошибки веса будут корректироваться до тех пор, пока фактический выход не совпадет с желаемым выходом.

Перцептрон

Перцептрон, разработанный Фрэнком Розенблаттом с использованием модели Маккаллоха и Питтса, является основным операционным блоком искусственных нейронных сетей. Он использует правила контролируемого обучения и может классифицировать данные на два класса.

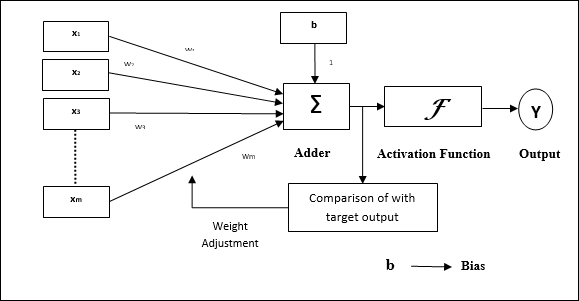
Рабочие характеристики перцептрона: он состоит из одного нейрона с произвольным числом входов и регулируемых весов, но выход нейрона равен 1 или 0 в зависимости от порога. Он также состоит из смещения, вес которого всегда равен 1. На следующем рисунке схематически показан перцептрон.

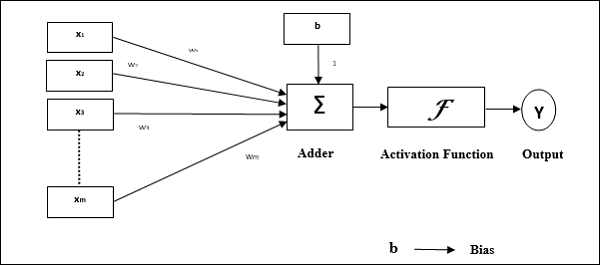
Таким образом, перцептрон имеет следующие три основных элемента:

• Links - У него будет набор соединительных звеньев, который имеет вес, включая смещение, всегда имеющее вес 1.

• Adder - Добавляет ввод после того, как они умножаются на их соответствующие веса.

• Activation function- Это ограничивает выход нейрона. Самая основная функция активации - это ступенчатая функция Хевисайда, имеющая два возможных выхода. Эта функция возвращает 1, если вход положительный, и 0 для любого отрицательного входа.

Алгоритм обучения

Сеть персептрона может быть обучена как для одного выходного устройства, так и для нескольких выходных устройств.

Алгоритм обучения для одного выходного устройства

Step 1 - Инициализируйте следующее, чтобы начать обучение -

• Weights
• Bias
• Скорость обучения $ \ alpha $

Для упрощения вычислений и простоты веса и смещения должны быть установлены равными 0, а скорость обучения должна быть установлена ​​равной 1.

Step 2 - Продолжайте шаги 3-8, если условие остановки не выполняется.

Step 3 - Продолжайте шаги 4-6 для каждого вектора тренировки. x.

Step 4 - Активируйте каждый входной блок следующим образом -

$$ x_ {i} \: = \: s_ {i} \ :( i \: = \: 1 \: to \: n) $$

Step 5 - Теперь получите чистый ввод со следующим соотношением -

$$ y_ {in} \: = \: b \: + \: \ displaystyle \ sum \ limits_ {i} ^ n x_ {i}. \: w_ {i} $$

Вот ‘b’ предвзятость и ‘n’ - общее количество входных нейронов.

Step 6 - Примените следующую функцию активации, чтобы получить окончательный результат.

$$ f (y_ {in}) \: = \: \ begin {cases} 1 & if \: y_ {in} \:> \: \ theta \\ 0 & if \: - \ theta \: \ leqslant \ : y_ {in} \: \ leqslant \: \ theta \\ - 1 & if \: y_ {in} \: <\: - \ theta \ end {cases} $$

Step 7 - Отрегулируйте вес и наклон следующим образом -

Case 1 - если y ≠ t тогда,

$$ w_ {i} (новый) \: = \: w_ {i} (старый) \: + \: \ alpha \: tx_ {i} $$

$$ b (новый) \: = \: b (старый) \: + \: \ alpha t $$

Case 2 - если y = t тогда,

$$ w_ {i} (новый) \: = \: w_ {i} (старый) $$

$$ b (новый) \: = \: b (старый) $$

Вот ‘y’ фактический выход и ‘t’ желаемый / целевой результат.

Step 8 - Проверка состояния остановки, которая может произойти, если вес не изменится.

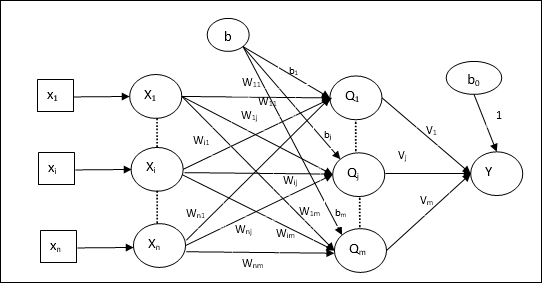
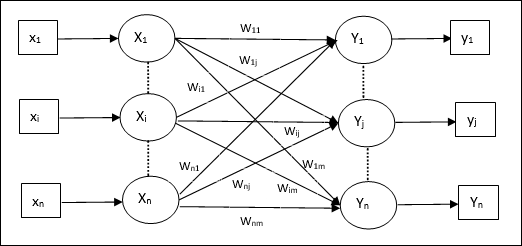
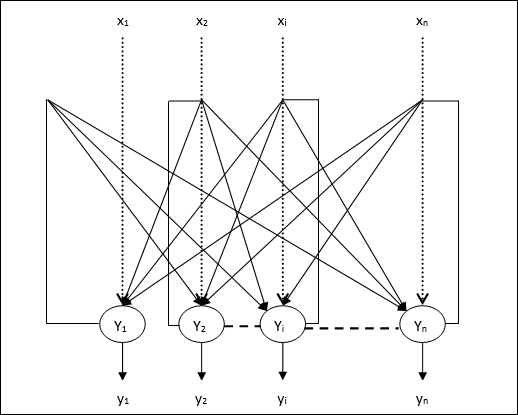
Алгоритм обучения для нескольких модулей вывода

Следующая диаграмма представляет собой архитектуру персептрона для нескольких выходных классов.

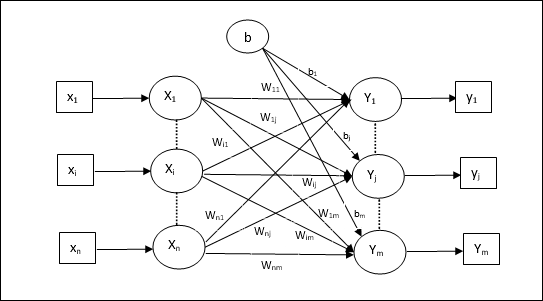
Step 1 - Инициализируйте следующее, чтобы начать обучение -

• Weights
• Bias
• Скорость обучения $ \ alpha $

Для упрощения вычислений и простоты веса и смещения должны быть установлены равными 0, а скорость обучения должна быть установлена ​​равной 1.

Step 2 - Продолжайте шаги 3-8, если условие остановки не выполняется.

Step 3 - Продолжайте шаги 4-6 для каждого вектора тренировки. x.

Step 4 - Активируйте каждый входной блок следующим образом -

$$ x_ {i} \: = \: s_ {i} \ :( i \: = \: 1 \: to \: n) $$

Step 5 - Получите чистый ввод со следующим соотношением -

$$ y_ {in} \: = \: b \: + \: \ displaystyle \ sum \ limits_ {i} ^ n x_ {i} \: w_ {ij} $$

Вот ‘b’ предвзятость и ‘n’ - общее количество входных нейронов.

Step 6 - Примените следующую функцию активации, чтобы получить окончательный результат для каждого выходного устройства. j = 1 to m -

$$ f (y_ {in}) \: = \: \ begin {cases} 1 & if \: y_ {inj} \:> \: \ theta \\ 0 & if \: - \ theta \: \ leqslant \ : y_ {inj} \: \ leqslant \: \ theta \\ - 1 & if \: y_ {inj} \: <\: - \ theta \ end {cases} $$

Step 7 - Отрегулируйте вес и наклон для x = 1 to n и j = 1 to m следующим образом -

Case 1 - если y_j ≠ t_j тогда,

$$ w_ {ij} (новый) \: = \: w_ {ij} (старый) \: + \: \ alpha \: t_ {j} x_ {i} $$

$$ b_ {j} (новый) \: = \: b_ {j} (старый) \: + \: \ alpha t_ {j} $$

Case 2 - если y_j = t_j тогда,

$$ w_ {ij} (новый) \: = \: w_ {ij} (старый) $$

$$ b_ {j} (новый) \: = \: b_ {j} (старый) $$

Вот ‘y’ фактический выход и ‘t’ желаемый / целевой результат.

Step 8 - Проверка состояния остановки, которая произойдет, если вес не изменится.

Адаптивный линейный нейрон (Адалин)

Adaline, что означает Adaptive Linear Neuron, представляет собой сеть, состоящую из одного линейного блока. Он был разработан Уидроу и Хоффом в 1960 году. Вот некоторые важные моменты об Адалин:

• Он использует функцию биполярной активации.

• Он использует правило дельты для обучения, чтобы минимизировать среднеквадратическую ошибку (MSE) между фактическим выходом и желаемым / целевым выходом.

• Вес и смещение регулируются.

Архитектура

Базовая структура Adaline аналогична персептрону, имеющему дополнительный контур обратной связи, с помощью которого фактический результат сравнивается с желаемым / целевым выходом. После сравнения на основе алгоритма обучения веса и смещения будут обновлены.

Алгоритм обучения

Step 1 - Инициализируйте следующее, чтобы начать обучение -

• Weights
• Bias
• Скорость обучения $ \ alpha $

Для упрощения вычислений и простоты веса и смещения должны быть установлены равными 0, а скорость обучения должна быть установлена ​​равной 1.

Step 2 - Продолжайте шаги 3-8, если условие остановки не выполняется.

Step 3 - Продолжайте шаги 4-6 для каждой пары биполярных тренировок. s:t.

Step 4 - Активируйте каждый входной блок следующим образом -

$$ x_ {i} \: = \: s_ {i} \ :( i \: = \: 1 \: to \: n) $$

Step 5 - Получите чистый ввод со следующим соотношением -

$$ y_ {in} \: = \: b \: + \: \ displaystyle \ sum \ limits_ {i} ^ n x_ {i} \: w_ {i} $$

Вот ‘b’ предвзятость и ‘n’ - общее количество входных нейронов.

Step 6 - Примените следующую функцию активации, чтобы получить окончательный результат -

$$ f (y_ {in}) \: = \: \ begin {cases} 1 & if \: y_ {in} \: \ geqslant \: 0 \\ - 1 & if \: y_ {in} \: < \: 0 \ end {case} $$

Step 7 - Отрегулируйте вес и наклон следующим образом -

Case 1 - если y ≠ t тогда,

$$ w_ {i} (новый) \: = \: w_ {i} (старый) \: + \: \ alpha (t \: - \: y_ {in}) x_ {i} $$

$$ b (новый) \: = \: b (старый) \: + \: \ alpha (t \: - \: y_ {in}) $$

Case 2 - если y = t тогда,

$$ w_ {i} (новый) \: = \: w_ {i} (старый) $$

$$ b (новый) \: = \: b (старый) $$

Вот ‘y’ фактический выход и ‘t’ желаемый / целевой результат.

$ (t \: - \; y_ {in}) $ - вычисленная ошибка.

Step 8 - Тест на условие остановки, которое произойдет, если вес не изменится или максимальное изменение веса, произошедшее во время тренировки, меньше указанного допуска.

Множественный адаптивный линейный нейрон (Madaline)

Madaline, что расшифровывается как Multiple Adaptive Linear Neuron, представляет собой сеть, состоящую из множества Adaline параллельно. Он будет иметь один выходной блок. Некоторые важные моменты о Мадалин следующие:

• Это похоже на многослойный перцептрон, где Адалин будет действовать как скрытая единица между входом и слоем Мадалин.

• Веса и смещение между входным слоем и слоем Adaline, как мы видим в архитектуре Adaline, можно регулировать.

• Слои Adaline и Madaline имеют фиксированные веса и смещение 1.

• Тренировку можно проводить с помощью правила Дельты.

Архитектура

Архитектура Madaline состоит из “n” нейроны входного слоя, “m”нейроны слоя Adaline и 1 нейрон слоя Madaline. Слой Adaline можно рассматривать как скрытый, поскольку он находится между входным и выходным слоями, то есть слоем Madaline.

Алгоритм обучения

К настоящему моменту мы знаем, что нужно настраивать только веса и смещение между входом и слоем Adaline, а веса и смещение между слоем Adaline и Madaline фиксированы.

Step 1 - Инициализируйте следующее, чтобы начать обучение -

• Weights
• Bias
• Скорость обучения $ \ alpha $

Для упрощения вычислений и простоты веса и смещения должны быть установлены равными 0, а скорость обучения должна быть установлена ​​равной 1.

Step 2 - Продолжайте шаги 3-8, если условие остановки не выполняется.

Step 3 - Продолжайте шаги 4-6 для каждой пары биполярных тренировок. s:t.

Step 4 - Активируйте каждый входной блок следующим образом -

$$ x_ {i} \: = \: s_ {i} \ :( i \: = \: 1 \: to \: n) $$

Step 5 - Получите чистый ввод на каждом скрытом слое, то есть слое Adaline со следующим соотношением -

$$ Q_ {inj} \: = \: b_ {j} \: + \: \ displaystyle \ sum \ limits_ {i} ^ n x_ {i} \: w_ {ij} \: \: \: j \: = \: 1 \: к \: m $$

Вот ‘b’ предвзятость и ‘n’ - общее количество входных нейронов.

Step 6 - Примените следующую функцию активации, чтобы получить окончательный результат на слоях Adaline и Madaline -

$$ f (x) \: = \: \ begin {cases} 1 & if \: x \: \ geqslant \: 0 \\ - 1 & if \: x \: <\: 0 \ end {cases} $ $

Вывод в скрытом (Adaline) блоке

$$ Q_ {j} \: = \: f (Q_ {inj}) $$

Окончательный вывод сети

$$ y \: = \: f (y_ {in}) $$

i.e. $ \: \: y_ {inj} \: = \: b_ {0} \: + \: \ sum_ {j = 1} ^ m \: Q_ {j} \: v_ {j} $

Step 7 - Рассчитайте ошибку и отрегулируйте веса следующим образом -

Case 1 - если y ≠ t и t = 1 тогда,

$$ w_ {ij} (новый) \: = \: w_ {ij} (старый) \: + \: \ alpha (1 \: - \: Q_ {inj}) x_ {i} $$

$$ b_ {j} (новый) \: = \: b_ {j} (старый) \: + \: \ alpha (1 \: - \: Q_ {inj}) $$

В этом случае веса будут обновлены Q_j где чистый ввод близок к 0, потому что t = 1.

Case 2 - если y ≠ t и t = -1 тогда,

$$ w_ {ik} (новый) \: = \: w_ {ik} (старый) \: + \: \ alpha (-1 \: - \: Q_ {ink}) x_ {i} $$

$$ b_ {k} (новый) \: = \: b_ {k} (старый) \: + \: \ alpha (-1 \: - \: Q_ {ink}) $$

В этом случае веса будут обновлены Q_k где чистый вход положительный, потому что t = -1.

Вот ‘y’ фактический выход и ‘t’ желаемый / целевой результат.

Case 3 - если y = t тогда

Вес не изменится.

Step 8 - Тест на условие остановки, которое произойдет, если вес не изменится или максимальное изменение веса, произошедшее во время тренировки, меньше указанного допуска.

Нейронные сети обратного распространения

Нейронная сеть обратного распространения (BPN) - это многослойная нейронная сеть, состоящая из входного слоя, по крайней мере, одного скрытого слоя и выходного слоя. Как следует из названия, в этой сети будет происходить обратное распространение. Ошибка, которая рассчитывается на выходном уровне путем сравнения целевого и фактического выходных данных, будет распространяться обратно на входной уровень.

Архитектура

Как показано на схеме, архитектура BPN имеет три взаимосвязанных уровня, на которых установлены веса. Скрытый слой, а также выходной слой также имеют смещение, вес которого всегда равен 1. Как видно из схемы, работа БПН проходит в два этапа. Одна фаза отправляет сигнал от входного слоя к выходному слою, а другая фаза назад передает ошибку от выходного слоя к входному слою.

Алгоритм обучения

Для обучения BPN будет использовать двоичную сигмовидную функцию активации. Обучение BPN будет состоять из трех этапов.

• Phase 1 - Фаза прямой связи

• Phase 2 - Обратное распространение ошибки

• Phase 3 - Обновление весов

Все эти шаги будут заключены в алгоритме следующим образом

Step 1 - Инициализируйте следующее, чтобы начать обучение -

• Weights
• Скорость обучения $ \ alpha $

Для облегчения расчета и простоты возьмите несколько небольших случайных значений.

Step 2 - Продолжайте шаги 3-11, если условие остановки не выполняется.

Step 3 - Продолжайте шаги 4-10 для каждой тренировочной пары.

Фаза 1

Step 4 - Каждый входной блок принимает входной сигнал x_i и отправляет его в скрытый блок для всех i = 1 to n

Step 5 - Рассчитайте чистый ввод в скрытом блоке, используя следующее соотношение -

$$ Q_ {inj} \: = \: b_ {0j} \: + \: \ sum_ {i = 1} ^ n x_ {i} v_ {ij} \: \: \: \: j \: = \ : 1 \: к \: p $$

Вот b_0j это уклон на скрытую единицу, v_ij вес на j единица скрытого слоя, исходящая из i единица входного слоя.

Теперь рассчитайте чистый выпуск, применив следующую функцию активации

$$ Q_ {j} \: = \: f (Q_ {inj}) $$

Отправьте эти выходные сигналы блоков скрытого слоя в блоки выходного слоя.

Step 6 - Рассчитайте чистый ввод в единице выходного слоя, используя следующее соотношение:

$$ y_ {ink} \: = \: b_ {0k} \: + \: \ sum_ {j = 1} ^ p \: Q_ {j} \: w_ {jk} \: \: k \: = \ : 1 \: в \: m $$

Вот b_0k ⁡ - смещение на выходе блока, w_jk вес на k единица выходного слоя из j единица скрытого слоя.

Рассчитайте чистый выпуск, применив следующую функцию активации

$$ y_ {k} \: = \: f (y_ {ink}) $$

Фаза 2

Step 7 - Вычислите член исправления ошибок в соответствии с целевым шаблоном, полученным на каждом выходном блоке, следующим образом:

$$ \ delta_ {k} \: = \ :( t_ {k} \: - \: y_ {k}) f ^ {'} (y_ {ink}) $$

Исходя из этого, обновите вес и смещение следующим образом:

$$ \ Delta v_ {jk} \: = \: \ alpha \ delta_ {k} \: Q_ {ij} $$

$$ \ Delta b_ {0k} \: = \: \ alpha \ delta_ {k} $$

Затем отправьте $ \ delta_ {k} $ обратно на скрытый слой.

Step 8 - Теперь каждый скрытый блок будет суммой его дельта-входов от выходных блоков.

$$ \ delta_ {inj} \: = \: \ displaystyle \ sum \ limits_ {k = 1} ^ m \ delta_ {k} \: w_ {jk} $$

Срок погрешности можно рассчитать следующим образом -

$$ \ delta_ {j} \: = \: \ delta_ {inj} f ^ {'} (Q_ {inj}) $$

Исходя из этого, обновите вес и смещение следующим образом:

$$ \ Delta w_ {ij} \: = \: \ alpha \ delta_ {j} x_ {i} $$

$$ \ Delta b_ {0j} \: = \: \ alpha \ delta_ {j} $$

Фаза 3

Step 9 - Каждый выходной блок (y_kk = 1 to m) обновляет вес и смещение следующим образом -

$$ v_ {jk} (новый) \: = \: v_ {jk} (старый) \: + \: \ Delta v_ {jk} $$

$$ b_ {0k} (новый) \: = \: b_ {0k} (старый) \: + \: \ Delta b_ {0k} $$

Step 10 - Каждый выходной блок (z_jj = 1 to p) обновляет вес и смещение следующим образом -

$$ w_ {ij} (новый) \: = \: w_ {ij} (старый) \: + \: \ Delta w_ {ij} $$

$$ b_ {0j} (новый) \: = \: b_ {0j} (старый) \: + \: \ Delta b_ {0j} $$

Step 11 - Проверьте условие остановки, которое может быть либо количеством достигнутых эпох, либо целевым выходом, совпадающим с фактическим выходом.

Обобщенное правило дельта-обучения

Правило дельты работает только для выходного слоя. С другой стороны, обобщенное правило дельты, также называемоеback-propagation Правило - это способ создания желаемых значений скрытого слоя.

Математическая формулировка

Для функции активации $ y_ {k} \: = \: f (y_ {ink}) $ вывод сетевого входа на скрытом слое, а также на выходном слое может быть задан как

$$ y_ {чернила} \: = \: \ displaystyle \ sum \ limits_i \: z_ {i} w_ {jk} $$

И $ \: \: y_ {inj} \: = \: \ sum_i x_ {i} v_ {ij} $

Теперь ошибка, которую необходимо минимизировать, равна

$$ E \: = \: \ гидроразрыва {1} {2} \ displaystyle \ sum \ limits_ {k} \: [t_ {k} \: - \: y_ {k}] ^ 2 $$

Используя цепное правило, мы имеем

$$ \ frac {\ partial E} {\ partial w_ {jk}} \: = \: \ frac {\ partial} {\ partial w_ {jk}} (\ frac {1} {2} \ displaystyle \ sum \ limit_ {k} \: [t_ {k} \: - \: y_ {k}] ^ 2) $$

$$ = \: \ frac {\ partial} {\ partial w_ {jk}} \ lgroup \ frac {1} {2} [t_ {k} \: - \: t (y_ {ink})] ^ 2 \ rgroup $$

$$ = \: - [t_ {k} \: - \: y_ {k}] \ frac {\ partial} {\ partial w_ {jk}} f (y_ {ink}) $$

$$ = \: - [t_ {k} \: - \: y_ {k}] f (y_ {ink}) \ frac {\ partial} {\ partial w_ {jk}} (y_ {ink}) $$

$$ = \: - [t_ {k} \: - \: y_ {k}] f ^ {'} (y_ {ink}) z_ {j} $$

Теперь скажем $ \ delta_ {k} \: = \: - [t_ {k} \: - \: y_ {k}] f ^ {'} (y_ {ink}) $

Веса на соединениях со скрытым блоком z_j может быть дан -

$$ \ frac {\ partial E} {\ partial v_ {ij}} \: = \: - \ displaystyle \ sum \ limits_ {k} \ delta_ {k} \ frac {\ partial} {\ partial v_ {ij} } \ :( y_ {ink}) $$

Подставив значение $ y_ {ink} $, мы получим следующее

$$ \ delta_ {j} \: = \: - \ displaystyle \ sum \ limits_ {k} \ delta_ {k} w_ {jk} f ^ {'} (z_ {inj}) $$

Обновление веса может быть выполнено следующим образом -

Для блока вывода -

$$ \ Delta w_ {jk} \: = \: - \ alpha \ frac {\ partial E} {\ partial w_ {jk}} $$

$$ = \: \ alpha \: \ delta_ {k} \: z_ {j} $$

Для скрытого блока -

$$ \ Delta v_ {ij} \: = \: - \ alpha \ frac {\ partial E} {\ partial v_ {ij}} $$

$$ = \: \ alpha \: \ delta_ {j} \: x_ {i} $$

Как следует из названия, этот тип обучения осуществляется без присмотра учителя. Этот процесс обучения независим. Во время обучения ИНС в условиях обучения без учителя входные векторы одного типа объединяются в кластеры. Когда применяется новый входной шаблон, нейронная сеть выдает выходной ответ, указывающий класс, к которому принадлежит входной шаблон. В этом случае не будет обратной связи из среды относительно того, каким должен быть желаемый результат и является ли он правильным или неправильным. Следовательно, в этом типе обучения сама сеть должна обнаруживать закономерности, особенности входных данных и отношения между входными данными и выходными.

Сети "победитель получает все"

Эти типы сетей основаны на правиле конкурентного обучения и будут использовать стратегию, при которой в качестве победителя выбирается нейрон с наибольшим суммарным входом. Связи между выходными нейронами показывают конкуренцию между ними, и один из них будет «включен», что означает, что он будет победителем, а другие будут «выключены».

Ниже приведены некоторые сети, основанные на этой простой концепции с использованием обучения без учителя.

Сеть Хэмминга

В большинстве нейронных сетей, использующих обучение без учителя, важно вычислять расстояние и выполнять сравнения. Такой тип сети называется сетью Хэмминга, где для каждого заданного входного вектора она будет сгруппирована в разные группы. Ниже приведены некоторые важные особенности сетей Хэмминга.

• Липпманн начал работать над сетями Хэмминга в 1987 году.

• Это однослойная сеть.

• Входы могут быть либо двоичными {0, 1}, либо биполярными {-1, 1}.

• Веса сети вычисляется по образцовым векторам.

• Это сеть с фиксированным весом, что означает, что веса останутся неизменными даже во время тренировки.

Макс Нетто

Это также сеть с фиксированным весом, которая служит подсетью для выбора узла с наибольшим входом. Все узлы полностью взаимосвязаны, и во всех этих взвешенных взаимосвязях существуют симметричные веса.

Архитектура

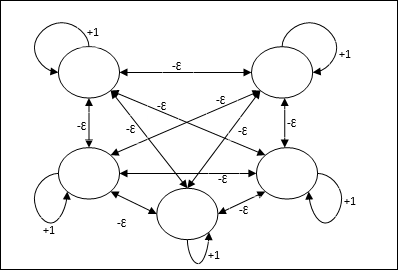
Он использует механизм, который представляет собой итеративный процесс, и каждый узел получает запрещающие входные данные от всех других узлов через соединения. Единственный узел, значение которого является максимальным, будет активным или победителем, а активации всех других узлов будут неактивными. Max Net использует функцию активации идентификатора с $$ f (x) \: = \: \ begin {cases} x & if \: x> 0 \\ 0 & if \: x \ leq 0 \ end {ases} $$

Задача этой сети решается с помощью веса самовозбуждения +1 и величины взаимного торможения, которая задается как [0 <ɛ <$ \ frac {1} {m} $], где “m” - общее количество узлов.

Конкурентное обучение в ИНС

Это связано с неконтролируемым обучением, в котором выходные узлы пытаются конкурировать друг с другом, чтобы представить входной шаблон. Чтобы понять это правило обучения, нам нужно понять конкурентную сеть, которая объясняется следующим образом:

Базовая концепция конкурентной сети

Эта сеть подобна однослойной сети с прямой связью, имеющей обратную связь между выходами. Связи между выходами являются тормозными, что показано пунктирными линиями, что означает, что конкуренты никогда не поддерживают себя.

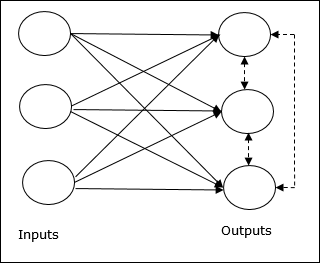
Основная концепция правила соревновательного обучения

Как было сказано ранее, между выходными узлами будет конкуренция, поэтому основная концепция заключается в том, что во время обучения выходной блок, который имеет наибольшую активацию для данного входного шаблона, будет объявлен победителем. Это правило также называется принципом «победитель получает все», потому что обновляется только нейрон-победитель, а остальные нейроны остаются неизменными.

Математическая формулировка

Ниже приведены три важных фактора для математической формулировки этого правила обучения.

• Условие быть победителем

  Предположим, если нейрон y_k хочет быть победителем, тогда будет следующее условие

  $$ y_ {k} \: = \: \ begin {cases} 1 & if \: v_ {k}> v_ {j} \: for \: all \: \: j, \: j \: \ neq \ : k \\ 0 и иначе \ end {case} $$

  Это означает, что если какой-либо нейрон, скажем, y_k хочет выиграть, то его индуцированное локальное поле (выход блока суммирования), скажем v_k, должен быть самым большим среди всех остальных нейронов сети.

• Условие общей суммы веса

  Другим ограничением правила конкурентного обучения является общая сумма весов конкретного выходного нейрона, равная 1. Например, если мы рассмотрим нейрон k тогда

  $$ \ displaystyle \ sum \ limits_ {k} w_ {kj} \: = \: 1 \: \: \: \: для \: all \: \: k $$

• Изменение веса победителя

  Если нейрон не реагирует на входной шаблон, то в этом нейроне не происходит обучения. Однако, если выигрывает конкретный нейрон, соответствующие веса корректируются следующим образом:

  $$ \ Delta w_ {kj} \: = \: \ begin {cases} - \ alpha (x_ {j} \: - \: w_ {kj}), & if \: нейрон \: k \: победит \\ 0 & if \: нейрон \: k \: loss \ end {cases} $$

  Здесь $ \ alpha $ - скорость обучения.

  Это ясно показывает, что мы отдаем предпочтение победившему нейрону, регулируя его вес, и если нейрон потерян, нам не нужно беспокоиться о корректировке его веса.

Алгоритм кластеризации K-средних

K-means - один из самых популярных алгоритмов кластеризации, в котором мы используем концепцию процедуры разделения. Мы начинаем с начального раздела и многократно перемещаем шаблоны из одного кластера в другой, пока не получим удовлетворительный результат.

Алгоритм

Step 1 - Выбрать kточки как начальные центроиды. Инициализироватьk прототипы (w₁,…,w_k), например, мы можем идентифицировать их со случайно выбранными входными векторами -

$$ W_ {j} \: = \: i_ {p}, \: \: \: где \: j \: \ in \ lbrace1, ...., k \ rbrace \: и \: p \: \ в \ lbrace1, ...., n \ rbrace $$

Каждый кластер C_j связан с прототипом w_j.

Step 2 - Повторяйте шаги 3-5, пока E не перестанет уменьшаться или членство в кластере не перестанет меняться.

Step 3 - Для каждого входного вектора i_p где p ∈ {1,…,n}, положить i_p в кластере C_j* с ближайшим прототипом w_j* имея следующее отношение

$$ | i_ {p} \: - \: w_ {j *} | \: \ leq \: | i_ {p} \: - \: w_ {j} |, \: j \: \ in \ lbrace1, ...., k \ rbrace $$

Step 4 - Для каждого кластера C_j, где j ∈ { 1,…,k}, обновите прототип w_j быть центроидом всех выборок в настоящее время C_j , так что

$$ w_ {j} \: = \: \ sum_ {i_ {p} \ in C_ {j}} \ frac {i_ {p}} {| C_ {j} |} $$

Step 5 - Вычислите полную ошибку квантования следующим образом -

$$ E \: = \: \ sum_ {j = 1} ^ k \ sum_ {i_ {p} \ in w_ {j}} | i_ {p} \: - \: w_ {j} | ^ 2 $$

Неокогнитрон

Это многоуровневая сеть с прямой связью, разработанная Фукусимой в 1980-х годах. Эта модель основана на обучении с учителем и используется для распознавания визуальных образов, в основном рукописных символов. По сути, это расширение сети Cognitron, которая также была разработана Фукусимой в 1975 году.

Архитектура

Это иерархическая сеть, состоящая из множества уровней, и на этих уровнях существует локальная схема подключения.

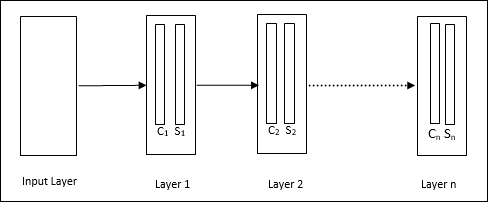
Как мы видели на приведенной выше диаграмме, неокогнитрон разделен на разные связанные слои, и каждый слой имеет две ячейки. Объяснение этих ячеек следующее -

S-Cell - Это называется простой клеткой, которая обучается реагировать на определенный паттерн или группу паттернов.

C-Cell- Это называется сложной ячейкой, которая объединяет вывод S-ячейки и одновременно уменьшает количество единиц в каждом массиве. В другом смысле C-cell вытесняет результат S-cell.

Алгоритм обучения

Обнаружено, что обучение неокогнитрона идет слой за слоем. Веса от входного слоя до первого слоя обучаются и замораживаются. Затем тренируются веса с первого уровня на второй и так далее. Внутренние вычисления между S-ячейкой и Ccell зависят от весов, полученных от предыдущих уровней. Следовательно, мы можем сказать, что алгоритм обучения зависит от вычислений для S-ячейки и C-ячейки.

Расчеты в S-ячейке

S-клетка обладает возбуждающим сигналом, полученным от предыдущего слоя, и обладает тормозными сигналами, полученными в том же слое.

$$ \ theta = \: \ sqrt {\ sum \ sum t_ {i} c_ {i} ^ 2} $$

Вот, t_i фиксированный вес и c_i это выход из C-ячейки.

Масштабированный вход S-ячейки можно рассчитать следующим образом:

$$ x \: = \: \ frac {1 \: + \: e} {1 \: + \: vw_ {0}} \: - \: 1 $$

Здесь $ e \: = \: \ sum_i c_ {i} w_ {i} $

w_i - это вес, скорректированный с C-ячейки на S-ячейку.

w₀ - вес, регулируемый между входом и S-ячейкой.

v это возбуждающий вход от C-клетки.

Активация выходного сигнала:

$$ s \: = \: \ begin {cases} x, & if \: x \ geq 0 \\ 0, & if \: x <0 \ end {cases} $$

Расчеты в C-cell

Чистый вклад C-слоя равен

$$ C \: = \: \ Displaystyle \ сумма \ limits_i s_ {i} x_ {i} $$

Вот, s_i это выход из S-ячейки и x_i - фиксированный вес от S-ячейки до C-ячейки.

Окончательный результат выглядит следующим образом -

$$ C_ {out} \: = \: \ begin {cases} \ frac {C} {a + C}, & if \: C> 0 \\ 0, и иначе \ end {ases} $$

Вот ‘a’ - параметр, который зависит от производительности сети.

Векторное квантование обучения (LVQ), отличное от векторного квантования (VQ) и самоорганизующихся карт Кохонена (KSOM), в основном представляет собой конкурентную сеть, в которой используется контролируемое обучение. Мы можем определить это как процесс классификации паттернов, где каждая единица вывода представляет класс. Поскольку она использует контролируемое обучение, сети будет предоставлен набор обучающих шаблонов с известной классификацией вместе с начальным распределением выходного класса. После завершения процесса обучения LVQ классифицирует входной вектор, назначая его тому же классу, что и выходной блок.

Архитектура

На следующем рисунке показана архитектура LVQ, которая очень похожа на архитектуру KSOM. Как видим, есть“n” количество единиц ввода и “m”количество единиц вывода. Слои полностью соединены между собой, на них есть утяжелители.

Используемые параметры

Ниже приведены параметры, используемые в процессе обучения LVQ, а также в блок-схеме.

• x= обучающий вектор (x ₁ , ..., x _i , ..., x _n )

• T = класс для обучающего вектора x

• w_j = вектор веса для j^th блок вывода

• C_j = класс, связанный с j^th блок вывода

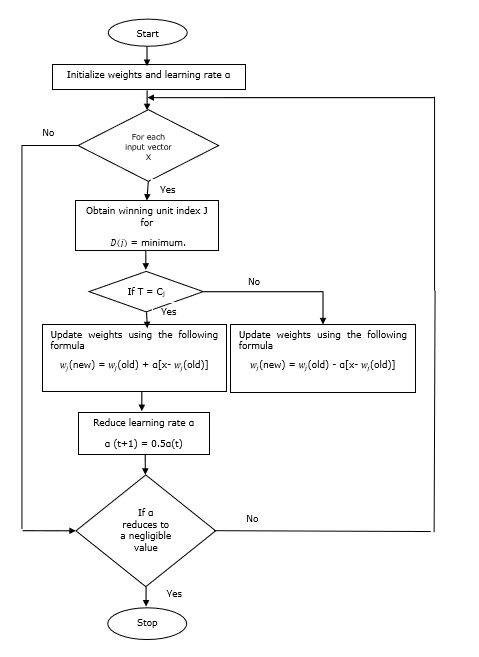
Алгоритм обучения

Step 1 - Инициализировать опорные векторы, что можно сделать следующим образом -

• Step 1(a) - Из заданного набора обучающих векторов возьмите первый «m”(Количество кластеров) обучающих векторов и использовать их как весовые векторы. Остальные векторы можно использовать для обучения.

• Step 1(b) - Назначьте начальный вес и классификацию случайным образом.

• Step 1(c) - Применить метод кластеризации K-средних.

Step 2 - Инициализировать опорный вектор $ \ alpha $

Step 3 - Продолжите с шагов 4-9, если условие остановки этого алгоритма не выполнено.

Step 4 - Выполните шаги 5-6 для каждого входного вектора обучения. x.

Step 5 - Вычислить квадрат евклидова расстояния для j = 1 to m и i = 1 to n

$$ D (j) \: = \: \ displaystyle \ sum \ limits_ {i = 1} ^ n \ displaystyle \ sum \ limits_ {j = 1} ^ m (x_ {i} \: - \: w_ {ij) }) ^ 2 $$

Step 6 - Получить победный отряд J где D(j) минимум.

Step 7 - Вычислите новый вес выигрышной единицы по следующей формуле -

если T = C_j затем $ w_ {j} (новый) \: = \: w_ {j} (старый) \: + \: \ alpha [x \: - \: w_ {j} (старый)] $

если T ≠ C_j затем $ w_ {j} (новый) \: = \: w_ {j} (старый) \: - \: \ alpha [x \: - \: w_ {j} (старый)] $

Step 8 - Уменьшить скорость обучения $ \ alpha $.

Step 9- Проверить состояние остановки. Это может быть следующее -

• Достигнуто максимальное количество эпох.
• Скорость обучения снизилась до незначительного значения.

Схема

Варианты

Три других варианта, а именно LVQ2, LVQ2.1 и LVQ3, были разработаны Кохоненом. Сложность во всех этих трех вариантах из-за концепции, которую выучат победитель, а также занявший второе место отряд, больше, чем в LVQ.

LVQ2

Как обсуждалось, в концепции других вариантов LVQ выше, состояние LVQ2 формируется окном. Это окно будет основано на следующих параметрах -

• x - текущий входной вектор

• y_c - опорный вектор, ближайший к x

• y_r - другой опорный вектор, ближайший к x

• d_c - расстояние от x к y_c

• d_r - расстояние от x к y_r

Входной вектор x падает в окно, если

$$ \ frac {d_ {c}} {d_ {r}} \:> \: 1 \: - \: \ theta \: \: и \: \: \ frac {d_ {r}} {d_ {c }} \:> \: 1 \: + \: \ theta $$

Здесь $ \ theta $ - количество обучающих выборок.

Обновление можно выполнить по следующей формуле -

$ y_ {c} (t \: + \: 1) \: = \: y_ {c} (t) \: + \: \ alpha (t) [x (t) \: - \: y_ {c} (t)] $ (belongs to different class)

$ y_ {r} (t \: + \: 1) \: = \: y_ {r} (t) \: + \: \ alpha (t) [x (t) \: - \: y_ {r} (t)] $ (belongs to same class)

Здесь $ \ alpha $ - скорость обучения.

LVQ2.1

В LVQ2.1 мы возьмем два ближайших вектора, а именно y_c1 и y_c2 и условие для окна следующее -

$$ Min \ begin {bmatrix} \ frac {d_ {c1}} {d_ {c2}}, \ frac {d_ {c2}} {d_ {c1}} \ end {bmatrix} \:> \ :( 1 \ : - \: \ theta) $$

$$ Max \ begin {bmatrix} \ frac {d_ {c1}} {d_ {c2}}, \ frac {d_ {c2}} {d_ {c1}} \ end {bmatrix} \: <\ :( 1 \ : + \: \ theta) $$

Обновление можно выполнить по следующей формуле -

$ y_ {c1} (t \: + \: 1) \: = \: y_ {c1} (t) \: + \: \ alpha (t) [x (t) \: - \: y_ {c1} (t)] $ (belongs to different class)

$ y_ {c2} (t \: + \: 1) \: = \: y_ {c2} (t) \: + \: \ alpha (t) [x (t) \: - \: y_ {c2} (t)] $ (belongs to same class)

Здесь $ \ alpha $ - скорость обучения.

LVQ3

В LVQ3 мы возьмем два ближайших вектора, а именно y_c1 и y_c2 и условие для окна следующее -

$$ Min \ begin {bmatrix} \ frac {d_ {c1}} {d_ {c2}}, \ frac {d_ {c2}} {d_ {c1}} \ end {bmatrix} \:> \ :( 1 \ : - \: \ theta) (1 \: + \: \ theta) $$

Здесь $ \ theta \ приблизительно 0,2 $

Обновление можно выполнить по следующей формуле -

$ y_ {c1} (t \: + \: 1) \: = \: y_ {c1} (t) \: + \: \ beta (t) [x (t) \: - \: y_ {c1} (t)] $ (belongs to different class)

$ y_ {c2} (t \: + \: 1) \: = \: y_ {c2} (t) \: + \: \ beta (t) [x (t) \: - \: y_ {c2} (t)] $ (belongs to same class)

Здесь $ \ beta $ - кратное скорости обучения $ \ alpha $ и $\beta\:=\:m \alpha(t)$ для каждого 0.1 < m < 0.5

Эта сеть была разработана Стивеном Гроссбергом и Гейл Карпентер в 1987 году. Она основана на конкуренции и использует модель обучения без учителя. Сети теории адаптивного резонанса (ART), как следует из названия, всегда открыты для нового обучения (адаптивного) без потери старых паттернов (резонанс). По сути, сеть ART представляет собой векторный классификатор, который принимает входной вектор и классифицирует его по одной из категорий в зависимости от того, какой из сохраненных шаблонов он больше всего напоминает.

Операционный директор

Основную операцию классификации ART можно разделить на следующие этапы:

• Recognition phase- Входной вектор сравнивается с классификацией, представленной в каждом узле выходного слоя. Выход нейрона становится «1», если он лучше всего соответствует применяемой классификации, в противном случае он становится «0».

• Comparison phase- На этом этапе выполняется сравнение входного вектора с вектором слоя сравнения. Условием сброса является то, что степень подобия будет меньше параметра бдительности.

• Search phase- На этом этапе сеть будет искать сброс, а также соответствие, выполненное на вышеуказанных этапах. Следовательно, если не будет сброса и совпадение будет хорошим, то классификация окончена. В противном случае процесс будет повторяться, и для поиска правильного соответствия необходимо будет отправить другой сохраненный шаблон.

ART1

Это тип ART, предназначенный для кластеризации двоичных векторов. Мы можем понять это по архитектуре.

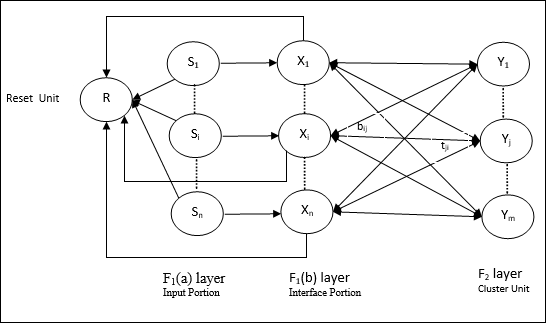
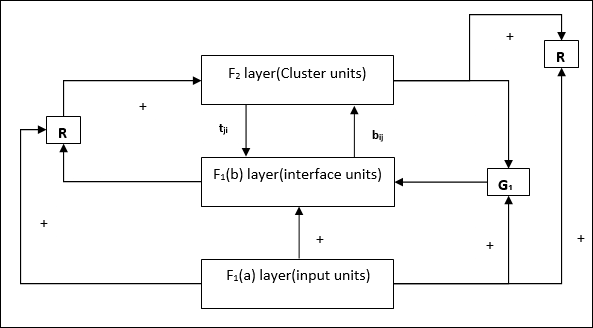
Архитектура ART1

Он состоит из следующих двух блоков -

Computational Unit - Он состоит из следующего -

• Input unit (F₁ layer) - Он также имеет следующие две части -

  • F₁(a) layer (Input portion)- В ART1 в этой части не будет обработки, а будут только входные векторы. Он подключен к слою F ₁ (b) (интерфейсная часть).

  • F₁(b) layer (Interface portion)- Эта часть объединяет сигнал входной части с сигналом слоя F ₂ . Слой F ₁ (b) соединен со слоем F ₂ через снизу вверх грузы.b_ijи слой F ₂ соединен со слоем F ₁ (b) через грузы сверху вниз.t_ji.

• Cluster Unit (F₂ layer)- Это соревновательный слой. Для изучения шаблона ввода выбирается блок, имеющий наибольший чистый входной сигнал. Активация всех остальных кластерных блоков установлена ​​на 0.

• Reset Mechanism- Работа этого механизма основана на сходстве между нисходящим весом и входным вектором. Теперь, если степень этого сходства меньше, чем параметр бдительности, то кластеру не разрешается изучать паттерн, и наступает отдых.

Supplement Unit - На самом деле проблема с механизмом сброса заключается в том, что слой F₂должны быть запрещены при определенных условиях, а также должны быть доступны, когда происходит некоторое обучение. Вот почему два дополнительных блока, а именно,G₁ и G₂ добавляется вместе с блоком сброса, R. Они называютсяgain control units. Эти устройства принимают и отправляют сигналы другим устройствам, присутствующим в сети.‘+’ указывает на возбуждающий сигнал, а ‘−’ указывает на тормозной сигнал.

Используемые параметры

Используются следующие параметры -

• n - Количество компонентов во входном векторе

• m - Максимальное количество кластеров, которые можно сформировать

• b_ij- Вес от слоя F ₁ (b) до слоя F ₂ , то есть веса снизу вверх

• t_ji- Вес от слоя F ₂ до F ₁ (b), то есть веса сверху вниз

• ρ - Параметр бдительности

• ||x|| - Норма вектора x

Алгоритм

Step 1 - Инициализируйте скорость обучения, параметр бдительности и веса следующим образом:

$$ \ alpha \:> \: 1 \: \: и \: \: 0 \: <\ rho \: \ leq \: 1 $$

$$ 0 \: <\: b_ {ij} (0) \: <\: \ frac {\ alpha} {\ alpha \: - \: 1 \: + \: n} \: \: и \: \: t_ {ij} (0) \: = \: 1 $$

Step 2 - Продолжайте шаги 3-9, если условие остановки не выполняется.

Step 3 - Продолжайте шаги 4-6 для каждого обучающего входа.

Step 4- Задайте активации всех блоков F ₁ (a) и F ₁ следующим образом

F₂ = 0 and F₁(a) = input vectors

Step 5- Входной сигнал от F ₁ (а) F ₁ (б) слой должен быть послан , как

$$ s_ {i} \: = \: x_ {i} $$

Step 6- Для каждого заблокированного узла F ₂

$ y_ {j} \: = \: \ sum_i b_ {ij} x_ {i} $ условие y_j ≠ -1

Step 7 - Выполните шаги 8-10, когда сброс верен.

Step 8 - Найти J за y_J ≥ y_j для всех узлов j

Step 9- Снова рассчитайте активацию на F ₁ (b) следующим образом

$$ x_ {i} \: = \: sitJi $$

Step 10 - Теперь, посчитав норму вектора x и вектор s, нам нужно проверить условие сброса следующим образом -

Если ||x||/ ||s|| <параметр бдительности ρ, Затем запретить узел J и переходите к шагу 7

Иначе, если ||x||/ ||s|| ≥ параметр бдительности ρ, затем продолжайте.

Step 11 - Обновление веса узла J можно сделать следующим образом -

$$ b_ {ij} (новый) \: = \: \ frac {\ alpha x_ {i}} {\ alpha \: - \: 1 \: + \: || x ||} $$

$$ t_ {ij} (новый) \: = \: x_ {i} $$

Step 12 - Необходимо проверить условие остановки для алгоритма, и оно может быть следующим:

• Нет никаких изменений в весе.
• Сброс для агрегатов не выполняется.
• Достигнуто максимальное количество эпох.

Предположим, у нас есть какой-то паттерн произвольных размеров, но он нам нужен в одном или двух измерениях. Тогда процесс отображения признаков будет очень полезен для преобразования широкого пространства шаблонов в типичное пространство признаков. Теперь возникает вопрос, почему нам нужна самоорганизующаяся карта функций? Причина в том, что наряду с возможностью преобразования произвольных измерений в 1-D или 2-D, он также должен иметь возможность сохранять топологию соседей.

Топологии соседей в Kohonen SOM

Могут быть разные топологии, но чаще всего используются следующие две топологии:

Топология прямоугольной сетки

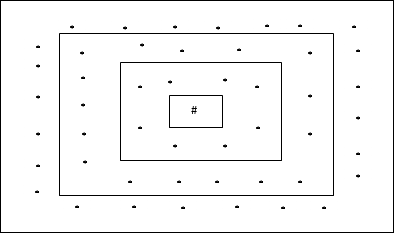
Эта топология имеет 24 узла в сетке расстояния-2, 16 узлов в сетке расстояния-1 и 8 узлов в сетке расстояния-0, что означает, что разница между каждой прямоугольной сеткой составляет 8 узлов. Победившая единица обозначена #.

Топология гексагональной сетки

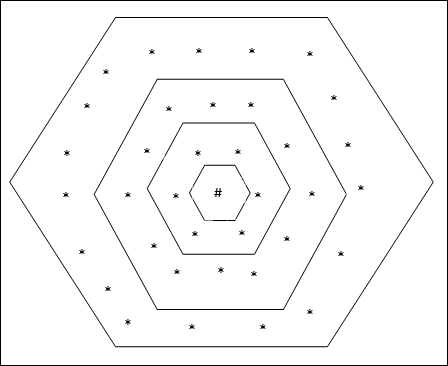
Эта топология имеет 18 узлов в сетке расстояния-2, 12 узлов в сетке расстояния-1 и 6 узлов в сетке расстояния-0, что означает, что разница между каждой прямоугольной сеткой составляет 6 узлов. Выигравшая единица обозначается #.

Архитектура

Архитектура KSOM аналогична архитектуре конкурентной сети. С помощью схем соседства, обсужденных ранее, обучение может происходить в расширенной области сети.

Алгоритм обучения

Step 1 - Инициализировать веса, скорость обучения α и топологическая схема окрестности.

Step 2 - Продолжайте шаги 3-9, если условие остановки не выполняется.

Step 3 - Продолжайте шаги 4-6 для каждого входного вектора x.

Step 4 - Вычислить квадрат евклидова расстояния для j = 1 to m

$$ D (j) \: = \: \ displaystyle \ sum \ limits_ {i = 1} ^ n \ displaystyle \ sum \ limits_ {j = 1} ^ m (x_ {i} \: - \: w_ {ij) }) ^ 2 $$

Step 5 - Получить победный отряд J где D(j) минимум.

Step 6 - Вычислите новый вес выигрышной единицы по следующей формуле -

$$ w_ {ij} (новый) \: = \: w_ {ij} (старый) \: + \: \ alpha [x_ {i} \: - \: w_ {ij} (старый)] $$

Step 7 - Обновить скорость обучения α следующим соотношением -

$$ \ alpha (t \: + \: 1) \: = \: 0.5 \ alpha t $$

Step 8 - Уменьшить радиус топологической схемы.

Step 9 - Проверьте состояние остановки сети.

Эти виды нейронных сетей работают на основе ассоциации шаблонов, что означает, что они могут хранить различные шаблоны, и во время выдачи выходных данных они могут создавать один из сохраненных шаблонов, сопоставляя их с заданным входным шаблоном. Эти типы воспоминаний также называютContent-Addressable Memory(САМ). Ассоциативная память выполняет параллельный поиск с сохраненными шаблонами в виде файлов данных.

Ниже приведены два типа ассоциативных воспоминаний, которые мы можем наблюдать:

• Автоассоциативная память
• Гетеро ассоциативная память

Автоассоциативная память

Это однослойная нейронная сеть, в которой входной обучающий вектор и выходной целевой вектор совпадают. Веса определены таким образом, чтобы сеть сохраняла набор шаблонов.

Архитектура

Как показано на следующем рисунке, архитектура сети автоассоциативной памяти имеет ‘n’ количество входных обучающих векторов и т.п. ‘n’ количество выходных целевых векторов.

Алгоритм обучения

Для обучения эта сеть использует правило обучения Хебба или Дельта.

Step 1 - Обнулить все веса как w_ij = 0 (i = 1 to n, j = 1 to n)

Step 2 - Выполните шаги 3-4 для каждого входного вектора.

Step 3 - Активируйте каждый входной блок следующим образом -

$$ x_ {i} \: = \: s_ {i} \ :( i \: = \: 1 \: to \: n) $$

Step 4 - Активируйте каждый выходной блок следующим образом -

$$ y_ {j} \: = \: s_ {j} \ :( j \: = \: 1 \: to \: n) $$

Step 5 - Отрегулируйте веса следующим образом -

$$ w_ {ij} (новый) \: = \: w_ {ij} (старый) \: + \: x_ {i} y_ {j} $$

Алгоритм тестирования

Step 1 - Установите веса, полученные во время тренировки, по правилу Хебба.

Step 2 - Выполните шаги 3-5 для каждого входного вектора.

Step 3 - Установите активацию входных единиц, равную активации входного вектора.

Step 4 - Рассчитайте чистый ввод для каждой единицы вывода j = 1 to n

$$ y_ {ING} \: = \: \ Displaystyle \ Sum \ limits_ {i = 1} ^ n x_ {i} w_ {ij} $$

Step 5 - Примените следующую функцию активации для расчета выхода

$$ y_ {j} \: = \: f (y_ {inj}) \: = \: \ begin {cases} +1 & if \: y_ {inj} \:> \: 0 \\ - 1 & if \: y_ {inj} \: \ leqslant \: 0 \ end {case} $$

Гетеро ассоциативная память

Подобно сети с автоматической ассоциативной памятью, это также однослойная нейронная сеть. Однако в этой сети входной обучающий вектор и выходные целевые векторы не совпадают. Веса определены таким образом, чтобы сеть сохраняла набор шаблонов. Гетероассоциативная сеть статична по своей природе, следовательно, не будет нелинейных операций и операций с задержкой.

Архитектура

Как показано на следующем рисунке, архитектура сети гетеро ассоциативной памяти имеет ‘n’ количество входных обучающих векторов и ‘m’ количество выходных целевых векторов.

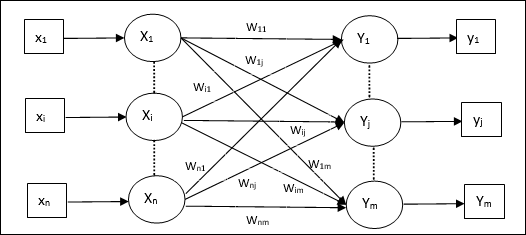
Алгоритм обучения

Для обучения эта сеть использует правило обучения Хебба или Дельта.

Step 1 - Обнулить все веса как w_ij = 0 (i = 1 to n, j = 1 to m)

Step 2 - Выполните шаги 3-4 для каждого входного вектора.

Step 3 - Активируйте каждый входной блок следующим образом -

$$ x_ {i} \: = \: s_ {i} \ :( i \: = \: 1 \: to \: n) $$

Step 4 - Активируйте каждый выходной блок следующим образом -

$$ y_ {j} \: = \: s_ {j} \ :( j \: = \: 1 \: to \: m) $$

Step 5 - Отрегулируйте веса следующим образом -

$$ w_ {ij} (новый) \: = \: w_ {ij} (старый) \: + \: x_ {i} y_ {j} $$

Алгоритм тестирования

Step 1 - Установите веса, полученные во время тренировки, по правилу Хебба.

Step 2 - Выполните шаги 3-5 для каждого входного вектора.

Step 3 - Установите активацию входных единиц, равную активации входного вектора.

Step 4 - Рассчитайте чистый ввод для каждой единицы вывода j = 1 to m;

$$ y_ {ING} \: = \: \ Displaystyle \ Sum \ limits_ {i = 1} ^ n x_ {i} w_ {ij} $$

Step 5 - Примените следующую функцию активации для расчета выхода

$$ y_ {j} \: = \: f (y_ {inj}) \: = \: \ begin {cases} +1 & if \: y_ {inj} \:> \: 0 \\ 0 & if \ : y_ {inj} \: = \: 0 \\ - 1 & if \: y_ {inj} \: <\: 0 \ end {cases} $$

Нейронная сеть Хопфилда была изобретена доктором Джоном Дж. Хопфилдом в 1982 году. Она состоит из одного слоя, который содержит один или несколько полностью связанных рекуррентных нейронов. Сеть Хопфилда обычно используется для задач автоматической ассоциации и оптимизации.

Дискретная сеть Хопфилда

Сеть Хопфилда, которая работает в режиме дискретных линий, или, другими словами, можно сказать, что шаблоны ввода и вывода являются дискретными векторными, которые могут быть либо двоичными (0,1), либо биполярными (+1, -1) по своей природе. Сеть имеет симметричные веса без самоподключений, т. Е.w_ij = w_ji и w_ii = 0.

Архитектура

Ниже приведены некоторые важные моменты, о которых следует помнить о дискретной сети Хопфилда.

• Эта модель состоит из нейронов с одним инвертирующим и одним неинвертирующим выходом.

• Выход каждого нейрона должен быть входом других нейронов, но не входом собственной личности.

• Вес / прочность соединения выражается как w_ij.

• Связи могут быть как возбуждающими, так и тормозящими. Было бы возбуждающе, если бы выход нейрона был таким же, как и вход, в противном случае - тормозящим.

• Гири должны быть симметричными, т.е. w_ij = w_ji

Выход из Y₁ собирается Y₂, Y_i и Y_n иметь вес w₁₂, w_1i и w_1nсоответственно. Точно так же на других дугах есть веса.

Алгоритм обучения

Во время обучения дискретной сети Хопфилда веса будут обновляться. Как мы знаем, у нас могут быть двоичные входные векторы, а также биполярные входные векторы. Следовательно, в обоих случаях обновления веса могут быть выполнены с помощью следующего соотношения

Case 1 - Шаблоны двоичного ввода

Для набора бинарных паттернов s(p), p = 1 to P

Вот, s(p) = s₁(p), s₂(p),..., s_i(p),..., s_n(p)

Матрица веса определяется выражением

$$ w_ {ij} \: = \: \ sum_ {p = 1} ^ P [2s_ {i} (p) - \: 1] [2s_ {j} (p) - \: 1] \: \: \: \: \: для \: i \: \ neq \: j $$

Case 2 - Биполярные входные шаблоны

Для набора бинарных паттернов s(p), p = 1 to P

Вот, s(p) = s₁(p), s₂(p),..., s_i(p),..., s_n(p)

Матрица веса определяется выражением

$$ w_ {ij} \: = \: \ sum_ {p = 1} ^ P [s_ {i} (p)] [s_ {j} (p)] \: \: \: \: \: для \ : i \: \ neq \: j $$

Алгоритм тестирования

Step 1 - Инициализировать веса, полученные из алгоритма обучения с использованием принципа Хеббиана.

Step 2 - Выполните шаги 3–9, если активации сети не консолидированы.

Step 3 - Для каждого входного вектора X, выполните шаги 4-8.

Step 4 - Сделайте начальную активацию сети равной внешнему входному вектору X следующим образом -

$$ y_ {i} \: = \: x_ {i} \: \: \: for \: i \: = \: 1 \: to \: n $$

Step 5 - Для каждого блока Y_i, выполните шаги 6–9.

Step 6 - Рассчитайте чистый ввод сети следующим образом -

$$ y_ {ini} \: = \: x_ {i} \: + \: \ displaystyle \ sum \ limits_ {j} y_ {j} w_ {ji} $$

Step 7 - Для расчета выхода примените активацию к входу сети следующим образом:

$$ y_ {i} \: = \ begin {cases} 1 & if \: y_ {ini} \:> \: \ theta_ {i} \\ y_ {i} & if \: y_ {ini} \: = \: \ theta_ {i} \\ 0 & if \: y_ {ini} \: <\: \ theta_ {i} \ end {cases} $$

Здесь $ \ theta_ {i} $ - порог.

Step 8 - Транслировать этот вывод y_i ко всем остальным единицам.

Step 9 - Протестируйте сеть на предмет соединения.

Оценка энергетической функции

Энергетическая функция определяется как функция, которая является связанной и невозрастающей функцией состояния системы.

Энергетическая функция E_f⁡, ⁡ также называется Lyapunov function определяет устойчивость дискретной сети Хопфилда и характеризуется следующим образом:

$$ E_ {F} \: = \: - \ frac {1} {2} \ displaystyle \ sum \ limits_ {i = 1} ^ n \ displaystyle \ sum \ limits_ {j = 1} ^ n y_ {i} y_ {j} w_ {ij} \: - \: \ displaystyle \ sum \ limits_ {i = 1} ^ n x_ {i} y_ {i} \: + \: \ displaystyle \ sum \ limits_ {i = 1} ^ n \ theta_ {i} y_ {i} $$

Condition - В стабильной сети всякий раз, когда состояние узла изменяется, указанная выше функция энергии будет уменьшаться.

Предположим, когда узел i изменил состояние с $ y_i ^ {(k)} $ на $ y_i ^ {(k \: + \: 1)} $ ⁡ тогда изменение энергии $ \ Delta E_ {f} $ определяется следующим соотношением

$$ \ Delta E_ {f} \: = \: E_ {f} (y_i ^ {(k + 1)}) \: - \: E_ {f} (y_i ^ {(k)}) $$

$$ = \: - \ left (\ begin {array} {c} \ displaystyle \ sum \ limits_ {j = 1} ^ n w_ {ij} y_i ^ {(k)} \: + \: x_ {i} \: - \: \ theta_ {i} \ end {array} \ right) (y_i ^ {(k + 1)} \: - \: y_i ^ {(k)}) $$

$$ = \: - \ :( net_ {i}) \ Delta y_ {i} $$

Здесь $ \ Delta y_ {i} \: = \: y_i ^ {(k \: + \: 1)} \: - \: y_i ^ {(k)} $

Изменение энергии зависит от того факта, что только один блок может обновлять свою активацию за раз.

Непрерывная сеть Хопфилда

По сравнению с дискретной сетью Хопфилда, непрерывная сеть имеет время как непрерывную переменную. Он также используется в автоматических ассоциациях и задачах оптимизации, таких как задача коммивояжера.

Model - Модель или архитектуру можно построить путем добавления электрических компонентов, таких как усилители, которые могут отображать входное напряжение с выходным напряжением с помощью функции активации сигмоида.

Оценка энергетической функции

$$ E_f = \ frac {1} {2} \ displaystyle \ sum \ limits_ {i = 1} ^ n \ sum _ {\ substack {j = 1 \\ j \ ne i}} ^ n y_i y_j w_ {ij} - \ displaystyle \ sum \ limits_ {i = 1} ^ n x_i y_i + \ frac {1} {\ lambda} \ displaystyle \ sum \ limits_ {i = 1} ^ n \ sum _ {\ substack {j = 1 \\ j \ ne i}} ^ n w_ {ij} g_ {ri} \ int_ {0} ^ {y_i} a ^ {- 1} (y) dy $$

Вот λ параметр усиления и g_ri входная проводимость.

Это стохастические процессы обучения, имеющие рекуррентную структуру, и они являются основой ранних методов оптимизации, используемых в ИНС. Машина Больцмана была изобретена Джеффри Хинтоном и Терри Сейновски в 1985 году. Большую ясность можно заметить в словах Хинтона о машине Больцмана.

«Удивительной особенностью этой сети является то, что она использует только локально доступную информацию. Изменение веса зависит только от поведения двух единиц, которые оно соединяет, даже если это изменение оптимизирует глобальную меру »- Ackley, Hinton 1985.

Некоторые важные моменты о машине Больцмана -

• Они используют повторяющуюся структуру.

• Они состоят из стохастических нейронов, которые имеют одно из двух возможных состояний: 1 или 0.

• Некоторые из нейронов в этом состоянии адаптивны (свободное состояние), а некоторые зажаты (замороженное состояние).

• Если применить моделирование отжига к дискретной сети Хопфилда, то получится машина Больцмана.

Цель машины Больцмана

Основная цель машины Больцмана - оптимизировать решение проблемы. Работа машины Больцмана заключается в оптимизации веса и количества, связанных с этой конкретной проблемой.

Архитектура

На следующей диаграмме показана архитектура машины Больцмана. Из диаграммы видно, что это двумерный массив единиц. Здесь веса на взаимосвязи между блоками равны–p где p > 0. Веса самоподключений даютсяb где b > 0.

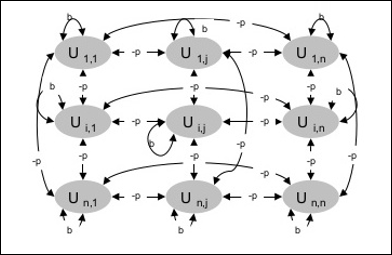
Алгоритм обучения

Поскольку мы знаем, что машины Больцмана имеют фиксированные веса, следовательно, не будет алгоритма обучения, поскольку нам не нужно обновлять веса в сети. Однако для тестирования сети мы должны установить веса, а также найти консенсусную функцию (CF).

Машина Больцмана имеет набор агрегатов U_i и U_j и имеет двунаправленные соединения на них.

• Мы рассматриваем фиксированный вес, скажем w_ij.

• w_ij ≠ 0 если U_i и U_j подключены.

• Также существует симметрия во взвешенном соединении, т. Е. w_ij знак равно w_ji.

• w_ii также существует, т. е. между блоками существует самоподключение.

• Для любого подразделения U_i, его состояние u_i будет либо 1, либо 0.

Основная цель машины Больцмана - максимизировать функцию консенсуса (CF), которая может быть задана следующим соотношением

$$ CF \: = \: \ displaystyle \ sum \ limits_ {i} \ displaystyle \ sum \ limits_ {j \ leqslant i} w_ {ij} u_ {i} u_ {j} $$

Теперь, когда состояние меняется либо с 1 на 0, либо с 0 на 1, изменение консенсуса может быть задано следующим соотношением:

$$ \ Delta CF \: = \ :( 1 \: - \: 2u_ {i}) (w_ {ij} \: + \: \ displaystyle \ sum \ limits_ {j \ neq i} u_ {i} w_ { ij}) $$

Вот u_i текущее состояние U_i.

Вариация коэффициента (1 - 2u_i) задается следующим соотношением -

$$ (1 \: - \: 2u_ {i}) \: = \: \ begin {cases} +1, & U_ {i} \: is \: current \: off \\ - 1, & U_ {i } \: is \: current \: on \ end {cases} $$

Обычно единица U_iне меняет своего состояния, но если это произойдет, то информация будет храниться локально для модуля. С этим изменением также повысится консенсус сети.

Вероятность того, что сеть примет изменение состояния устройства, определяется следующим соотношением:

$$ AF (i, T) \: = \: \ frac {1} {1 \: + \: exp [- \ frac {\ Delta CF (i)} {T}]} $$

Вот, T- управляющий параметр. Он будет уменьшаться, когда CF достигнет максимального значения.

Алгоритм тестирования

Step 1 - Инициализируйте следующее, чтобы начать обучение -

• Веса, представляющие ограничение проблемы
• Контрольный параметр T

Step 2 - Продолжайте шаги 3-8, если условие остановки не выполняется.

Step 3 - Выполните шаги 4-7.

Step 4 - Предположим, что одно из состояний изменило вес и выберите целое число I, J как случайные значения между 1 и n.

Step 5 - Рассчитайте изменение консенсуса следующим образом:

$$ \ Delta CF \: = \ :( 1 \: - \: 2u_ {i}) (w_ {ij} \: + \: \ displaystyle \ sum \ limits_ {j \ neq i} u_ {i} w_ { ij}) $$

Step 6 - Рассчитайте вероятность того, что эта сеть примет изменение состояния

$$ AF (i, T) \: = \: \ frac {1} {1 \: + \: exp [- \ frac {\ Delta CF (i)} {T}]} $$

Step 7 - Примите или отклоните это изменение следующим образом -

Case I - если R < AF, примите изменение.

Case II - если R ≥ AF, отклоните изменение.

Вот, R - случайное число от 0 до 1.

Step 8 - Уменьшите контрольный параметр (температуру) следующим образом -

T(new) = ⁡0.95T(old)

Step 9 - Проверьте условия остановки, которые могут быть следующими:

• Температура достигает заданного значения
• Состояние не меняется за указанное количество итераций.

Нейронная сеть Brain-State-in-a-Box (BSB) - это нелинейная автоассоциативная нейронная сеть, которая может быть расширена до гетероассоциации с двумя или более слоями. Он также похож на сеть Хопфилда. Он был предложен Дж. А. Андерсоном, Дж. У. Сильверстайном, С. А. Ритцем и Р. С. Джонсом в 1977 году.

Некоторые важные моменты, которые следует помнить о сети BSB -

• Это полностью связанная сеть с максимальным количеством узлов в зависимости от размерности. n входного пространства.

• Все нейроны обновляются одновременно.

• Нейроны принимают значения от -1 до +1.

Математические формулировки

Функция узла, используемая в сети BSB, представляет собой функцию линейного изменения, которую можно определить следующим образом:

$$ f (чистая) \: = \: min (1, \: max (-1, \: net)) $$

Эта функция линейного изменения ограничена и непрерывна.

Поскольку мы знаем, что каждый узел изменит свое состояние, это можно сделать с помощью следующего математического соотношения:

$$ x_ {t} (t \: + \: 1) \: = \: f \ left (\ begin {array} {c} \ displaystyle \ sum \ limits_ {j = 1} ^ n w_ {i, j } x_ {j} (t) \ end {array} \ right) $$

Вот, x_i(t) состояние i_th узел во время t.

Вес от i_th узел к j_th узел можно измерить следующим соотношением -

$$ w_ {ij} \: = \: \ frac {1} {P} \ displaystyle \ sum \ limits_ {p = 1} ^ P (v_ {p, i} \: v_ {p, j}) $$

Вот, P - количество биполярных тренировочных паттернов.

Оптимизация - это действие, направленное на то, чтобы сделать что-то, например дизайн, ситуацию, ресурсы и систему, максимально эффективными. Используя сходство между функцией стоимости и функцией энергии, мы можем использовать сильно взаимосвязанные нейроны для решения задач оптимизации. Такой вид нейронной сети представляет собой сеть Хопфилда, которая состоит из одного слоя, содержащего один или несколько полностью связанных рекуррентных нейронов. Это можно использовать для оптимизации.

Что следует помнить при использовании сети Хопфилда для оптимизации -

• Энергетическая функция сети должна быть минимальной.

• Он найдет удовлетворительное решение, а не выберет один из сохраненных шаблонов.

• Качество решения, найденного сетью Хопфилда, существенно зависит от начального состояния сети.

Проблема коммивояжера

Нахождение кратчайшего пути, пройденного продавцом, является одной из вычислительных задач, которую можно оптимизировать с помощью нейронной сети Хопфилда.

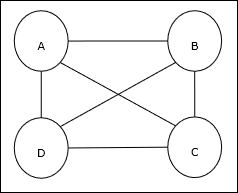
Базовая концепция TSP

Задача коммивояжера (TSP) - это классическая задача оптимизации, в которой продавец должен путешествовать. nгорода, которые связаны друг с другом, что позволяет минимизировать стоимость и пройденное расстояние. Например, продавец должен проехать группу из 4 городов A, B, C, D, и цель состоит в том, чтобы найти самый короткий круговой тур, ABC – D, чтобы минимизировать стоимость, которая также включает стоимость поездки из последний город D к первому городу A.

Матричное представление

Фактически каждый тур по ТСП n-го города можно выразить как n × n матрица, чья i_th строка описывает i_thрасположение города. Эта матрица,M, для 4 городов A, B, C, D можно выразить следующим образом:

$$ M = \ begin {bmatrix} A: & 1 & 0 & 0 & 0 \\ B: & 0 & 1 & 0 & 0 \\ C: & 0 & 0 & 1 & 0 \\ D: & 0 & 0 & 0 & 1 \ end {bmatrix} $$

Решение от Hopfield Network

При рассмотрении решения этой TSP сетью Хопфилда каждый узел в сети соответствует одному элементу в матрице.

Расчет функции энергии

Чтобы быть оптимизированным решением, функция энергии должна быть минимальной. На основе следующих ограничений мы можем вычислить функцию энергии следующим образом:

Ограничение-I

Первое ограничение, на основании которого мы будем вычислять функцию энергии, состоит в том, что один элемент должен быть равен 1 в каждой строке матрицы M а остальные элементы в каждой строке должны равняться 0потому что каждый город может фигурировать только в одной позиции в туре TSP. Это ограничение математически можно записать следующим образом:

$$ \ displaystyle \ sum \ limits_ {j = 1} ^ n M_ {x, j} \: = \: 1 \: для \: x \: \ in \: \ lbrace1, ..., n \ rbrace $ $

Теперь функция энергии, которая должна быть минимизирована на основе вышеуказанного ограничения, будет содержать член, пропорциональный -

$$ \ displaystyle \ sum \ limits_ {x = 1} ^ n \ left (\ begin {array} {c} 1 \: - \: \ displaystyle \ sum \ limits_ {j = 1} ^ n M_ {x, j } \ end {array} \ right) ^ 2 $$

Ограничение-II

Как мы знаем, в TSP один город может находиться в любой позиции тура, следовательно, в каждом столбце матрицы. M, один элемент должен быть равен 1, а другие элементы должны быть равны 0. Это ограничение математически можно записать следующим образом:

$$ \ displaystyle \ sum \ limits_ {x = 1} ^ n M_ {x, j} \: = \: 1 \: для \: j \: \ in \: \ lbrace1, ..., n \ rbrace $ $

Теперь функция энергии, которая должна быть минимизирована на основе вышеуказанного ограничения, будет содержать член, пропорциональный -

$$ \ displaystyle \ sum \ limits_ {j = 1} ^ n \ left (\ begin {array} {c} 1 \: - \: \ displaystyle \ sum \ limits_ {x = 1} ^ n M_ {x, j } \ end {array} \ right) ^ 2 $$

Расчет функции затрат

Предположим, что квадратная матрица (n × n) обозначается C обозначает матрицу затрат TSP для n города, где n > 0. Ниже приведены некоторые параметры при расчете функции стоимости.

• C_{x, y} - Элемент матрицы стоимости обозначает стоимость проезда из города x к y.

• Смежность элементов A и B может быть показана следующим соотношением -

$$ M_ {x, i} \: = \: 1 \: \: и \: \: M_ {y, i \ pm 1} \: = \: 1 $$

Как мы знаем, в Matrix выходное значение каждого узла может быть либо 0, либо 1, поэтому для каждой пары городов A, B мы можем добавить следующие члены к функции энергии:

$$ \ Displaystyle \ сумма \ пределы_ {я = 1} ^ n C_ {x, y} M_ {x, i} (M_ {y, i + 1} \: + \: M_ {y, i-1}) $$

На основе приведенной выше функции стоимости и значения ограничения конечная функция энергии E может быть дано следующим образом -

$$ E \: = \: \ frac {1} {2} \ displaystyle \ sum \ limits_ {i = 1} ^ n \ displaystyle \ sum \ limits_ {x} \ displaystyle \ sum \ limits_ {y \ neq x} C_ {x, y} M_ {x, i} (M_ {y, i + 1} \: + \: M_ {y, i-1}) \: + $$

$$ \: \ begin {bmatrix} \ gamma_ {1} \ displaystyle \ sum \ limits_ {x} \ left (\ begin {array} {c} 1 \: - \: \ displaystyle \ sum \ limits_ {i} M_ {x, i} \ end {array} \ right) ^ 2 \: + \: \ gamma_ {2} \ displaystyle \ sum \ limits_ {i} \ left (\ begin {array} {c} 1 \: - \ : \ displaystyle \ sum \ limits_ {x} M_ {x, i} \ end {array} \ right) ^ 2 \ end {bmatrix} $$

Вот, γ₁ и γ₂ - две константы взвешивания.

Метод повторного градиентного спуска

Градиентный спуск, также известный как наискорейший спуск, представляет собой итерационный алгоритм оптимизации для поиска локального минимума функции. Сводя к минимуму функцию, мы заботимся о том, чтобы минимизировать стоимость или ошибку (вспомните задачу коммивояжера). Он широко используется в глубоком обучении, что полезно в самых разных ситуациях. Здесь следует помнить, что нас интересует локальная оптимизация, а не глобальная.

Основная рабочая идея

Мы можем понять основную рабочую идею градиентного спуска с помощью следующих шагов:

• Во-первых, начните с первоначального предположения о решении.

• Затем возьмите градиент функции в этой точке.

• Позже повторите процесс, двигая решение в отрицательном направлении градиента.

Следуя вышеуказанным шагам, алгоритм в конечном итоге сойдется там, где градиент равен нулю.

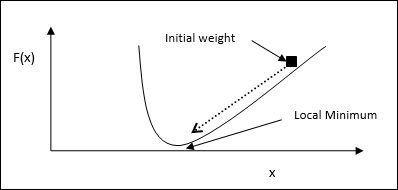
Математическая концепция

Предположим, у нас есть функция f(x)и мы пытаемся найти минимум этой функции. Ниже приведены шаги, чтобы найти минимумf(x).

• Сначала укажите начальное значение $ x_ {0} \: for \: x $

• Теперь возьмем градиент $ \ nabla f $ ⁡ функции, интуитивно понимая, что градиент даст наклон кривой при этом x и его направление будет указывать на увеличение функции, чтобы найти лучшее направление для ее минимизации.

• Теперь измените x следующим образом -

  $$ x_ {n \: + \: 1} \: = \: x_ {n} \: - \: \ theta \ nabla f (x_ {n}) $$

Вот, θ > 0 - скорость обучения (размер шага), заставляющая алгоритм делать небольшие скачки.

Оценка размера шага

На самом деле неправильный размер шага θмогут не достичь конвергенции, поэтому очень важен их тщательный выбор. При выборе размера шага необходимо помнить следующие моменты.

• Не выбирайте слишком большой размер шага, иначе он будет иметь негативное влияние, т.е. он будет расходиться, а не сходиться.

• Не выбирайте слишком маленький размер шага, иначе на схождение уйдет много времени.

Некоторые варианты выбора размера шага -

• Один из вариантов - выбрать фиксированный размер шага.

• Другой вариант - выбирать разный размер шага для каждой итерации.

Имитация отжига

Основная концепция имитационного отжига (SA) основана на отжиге в твердых телах. Если в процессе отжига мы нагреем металл выше температуры плавления и охладим его, то структурные свойства будут зависеть от скорости охлаждения. Можно также сказать, что SA моделирует металлургический процесс отжига.

Использование в ИНС

SA - это стохастический вычислительный метод, вдохновленный аналогией отжига, для аппроксимации глобальной оптимизации заданной функции. Мы можем использовать SA для обучения нейронных сетей с прямой связью.

Алгоритм

Step 1 - Создать случайное решение.

Step 2 - Рассчитайте его стоимость, используя некоторую функцию стоимости.

Step 3 - Создать случайное решение для соседей.

Step 4 - Рассчитайте стоимость нового решения с помощью той же функции стоимости.

Step 5 - Сравните стоимость нового решения со стоимостью старого решения следующим образом:

Если Cost_{New Solution} < Cost_{Old Solution} затем переходите к новому решению.

Step 6 - Проверить условие остановки, которое может быть максимальным числом достигнутых итераций или получить приемлемое решение.

Природа всегда была великим источником вдохновения для всего человечества. Генетические алгоритмы (ГА) - это алгоритмы поиска, основанные на концепциях естественного отбора и генетики. ГА - это подмножество гораздо более крупной ветви вычислений, известной какEvolutionary Computation.

GA был разработан Джоном Холландом и его студентами и коллегами из Мичиганского университета, в первую очередь Дэвидом Э. Голдбергом, и с тех пор с большим успехом опробовали различные задачи оптимизации.

В GA у нас есть пул или совокупность возможных решений данной проблемы. Затем эти решения подвергаются рекомбинации и мутации (как в естественной генетике), производя новых детей, и этот процесс повторяется в разных поколениях. Каждому индивиду (или возможному решению) присваивается значение пригодности (на основе его значения целевой функции), и более приспособленные индивидуумы получают более высокий шанс спариться и дать более «приспособленных» особей. Это соответствует дарвиновской теории «выживания сильнейшего».

Таким образом, мы продолжаем «развивать» лучших людей или решения на протяжении поколений, пока не достигнем критерия остановки.

Генетические алгоритмы достаточно рандомизированы по своей природе, однако они работают намного лучше, чем случайный локальный поиск (в котором мы просто пробуем различные случайные решения, отслеживая лучшие на данный момент), поскольку они также используют историческую информацию.

Преимущества ГА

ГА имеют различные преимущества, которые сделали их чрезвычайно популярными. К ним относятся -

• Не требует какой-либо производной информации (которая может быть недоступна для многих реальных проблем).

• Быстрее и эффективнее по сравнению с традиционными методами.

• Имеет очень хорошие параллельные возможности.

• Оптимизирует как непрерывные, так и дискретные функции, а также многокритериальные задачи.

• Предоставляет список «хороших» решений, а не одно решение.

• Всегда получает ответ на проблему, который со временем становится лучше.

• Полезно, когда пространство поиска очень велико и задействовано большое количество параметров.

Ограничения ГА

Как и любой метод, GA также имеет несколько ограничений. К ним относятся -

• ГА не подходят для всех проблем, особенно для простых задач, по которым доступна производная информация.

• Значение пригодности вычисляется многократно, что для некоторых задач может потребовать больших вычислительных ресурсов.

• Поскольку решение является стохастическим, нет никаких гарантий оптимальности или качества решения.

• Если не реализован должным образом, GA может не прийти к оптимальному решению.

GA - Мотивация

Генетические алгоритмы обладают способностью предоставлять «достаточно хорошее» решение «достаточно быстро». Это делает газ привлекательным для решения задач оптимизации. Причины, по которым необходимы ГА, следующие:

Решение сложных проблем

В информатике существует большой набор проблем, которые NP-Hard. По сути, это означает, что даже самым мощным вычислительным системам требуется очень много времени (даже годы!) Для решения этой проблемы. В таком сценарии ГА оказываются эффективным инструментом для обеспеченияusable near-optimal solutions в короткие сроки.

Неудача градиентных методов

Традиционные методы, основанные на исчислении, работают, начиная со случайной точки и двигаясь в направлении градиента, пока мы не достигнем вершины холма. Этот метод эффективен и очень хорошо работает для однопиковых целевых функций, таких как функция стоимости в линейной регрессии. Однако в большинстве реальных ситуаций у нас есть очень сложная проблема, называемая ландшафтами, состоящими из множества пиков и долин, что приводит к сбою таких методов, поскольку они страдают от присущей им тенденции застревать на локальных оптимумах, как показано на следующем рисунке.

Быстрое получение хорошего решения

Некоторые сложные задачи, такие как задача коммивояжера (TSP), имеют реальные приложения, такие как поиск пути и проектирование СБИС. Теперь представьте, что вы используете свою систему GPS-навигации, и требуется несколько минут (или даже несколько часов), чтобы вычислить «оптимальный» путь от источника до пункта назначения. Задержка в таких реальных приложениях неприемлема, и поэтому требуется «достаточно хорошее» решение, которое доставляется «быстро».

Как использовать GA для решения задач оптимизации?

Мы уже знаем, что оптимизация - это действие, направленное на то, чтобы сделать что-то, например дизайн, ситуацию, ресурсы и систему, максимально эффективными. Процесс оптимизации показан на следующей диаграмме.

Этапы механизма ГА для оптимизации процесса

Ниже приведены этапы использования механизма GA для оптимизации задач.

• Сгенерируйте начальную популяцию случайным образом.

• Выберите исходное решение с наилучшими значениями пригодности.

• Перекомбинируйте выбранные решения, используя операторы мутации и кроссовера.

• Вставьте потомство в популяцию.

• Теперь, если условие остановки выполнено, верните решение с наилучшим значением пригодности. В противном случае перейдите к шагу 2.

Прежде чем изучать области, в которых ИНС широко используется, нам необходимо понять, почему ИНС является предпочтительным выбором приложения.

Почему искусственные нейронные сети?

Нам нужно понять ответ на поставленный выше вопрос на примере человека. В детстве мы учились этому с помощью старших, в том числе родителей или учителей. Позже, путем самообучения или практики, мы продолжаем учиться на протяжении всей жизни. Ученые и исследователи также делают машину интеллектуальной, как и человека, и ИНС играет очень важную роль в этом по следующим причинам:

• С помощью нейронных сетей мы можем найти решение таких задач, для которых алгоритмический метод дорог или не существует.

• Нейронные сети могут учиться на примере, поэтому нам не нужно сильно его программировать.

• Нейронные сети имеют точность и значительно большую скорость, чем обычные.

Области применения

Ниже приведены некоторые из областей, в которых используется ИНС. Это говорит о том, что ИНС использует междисциплинарный подход к разработке и применению.

Распознавание речи

Речь играет важную роль во взаимодействии человека и человека. Поэтому для людей естественно ожидать речевого интерфейса с компьютером. В нынешнюю эпоху для общения с машинами людям по-прежнему нужны сложные языки, которые трудно выучить и использовать. Чтобы облегчить этот коммуникационный барьер, простым решением может быть общение на разговорном языке, понятном машине.

В этой области был достигнут большой прогресс, однако, такие системы все еще сталкиваются с проблемой ограниченного словарного запаса или грамматики, а также с проблемой переобучения системы для разных говорящих в разных условиях. ИНС играет важную роль в этой области. Следующие ИНС были использованы для распознавания речи -

• Многослойные сети

• Многослойные сети с повторяющимися подключениями

• Самоорганизующаяся карта объектов Кохонена

Наиболее полезной сетью для этого является карта самоорганизующихся функций Кохонена, которая вводится в виде коротких сегментов речевого сигнала. Он будет отображать тот же вид фонем, что и выходной массив, что называется методом извлечения признаков. После извлечения признаков с помощью некоторых акустических моделей в качестве внутренней обработки он распознает высказывание.

Распознавание персонажей

Это интересная проблема, которая относится к общей области распознавания образов. Многие нейронные сети были разработаны для автоматического распознавания рукописных символов, букв или цифр. Ниже приведены некоторые ИНС, которые использовались для распознавания символов.

• Многослойные нейронные сети, такие как нейронные сети обратного распространения.
• Neocognitron

Хотя нейронные сети с обратным распространением информации имеют несколько скрытых слоев, схема соединения от одного уровня к другому локализована. Точно так же неокогнитрон также имеет несколько скрытых слоев, и его обучение выполняется слой за слоем для таких приложений.

Заявление о проверке подписи

Подписи - один из наиболее полезных способов авторизации и аутентификации человека в юридических сделках. Техника проверки подписи не основана на видении.

Для этого приложения первый подход состоит в том, чтобы извлечь элемент или, скорее, набор геометрических элементов, представляющий подпись. С помощью этих наборов функций мы должны обучать нейронные сети, используя эффективный алгоритм нейронной сети. Эта обученная нейронная сеть будет классифицировать подпись как подлинную или поддельную на этапе проверки.

Распознавание человеческого лица

Это один из биометрических методов идентификации лица. Это типичная задача из-за характеристики изображений «без лица». Однако, если нейронная сеть хорошо обучена, то ее можно разделить на два класса, а именно изображения с лицами и изображения без лиц.

Во-первых, все входные изображения должны быть предварительно обработаны. Затем необходимо уменьшить размерность этого изображения. И, наконец, его необходимо классифицировать с помощью алгоритма обучения нейронной сети. Следующие нейронные сети используются для целей обучения с предварительно обработанным изображением -

• Полносвязная многослойная нейронная сеть с прямой связью, обученная с помощью алгоритма обратного распространения.

• Для уменьшения размерности используется анализ главных компонентов (PCA).