Цепные соединения в индукторах
Индуктор при включении в цепь может быть последовательным или параллельным. Дайте нам теперь знать, что произойдет с общими значениями тока, напряжения и сопротивления, если они будут подключены последовательно, а также при параллельном подключении.
Индукторы в серии
Давайте посмотрим, что происходит, когда несколько катушек индуктивности соединяются последовательно. Рассмотрим три резистора с разными номиналами, как показано на рисунке ниже.
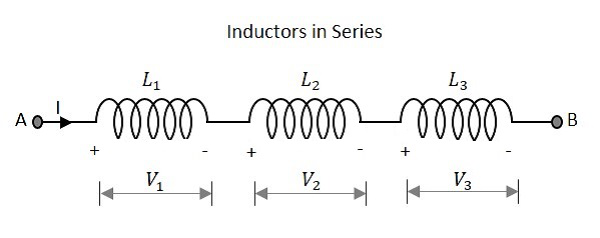
Индуктивность
Полная индуктивность цепи с последовательными индукторами равна сумме индивидуальных индуктивностей. Суммарное значение индуктивности сети, приведенное выше, равно
$$ L_ {T} \: \: = \: \: L_ {1} \: \: + \: \: L_ {2} \: \: + \: \: L_ {3} $$
Где L 1 - это индуктивность 1- го резистора, L 2 - это индуктивность 2- го резистора, а L 3 - индуктивность 3- го резистора в вышеуказанной сети.
вольтаж
Общее напряжение, которое появляется в цепи последовательных катушек индуктивности, складывается из падений напряжения на каждой отдельной индуктивности.
Общее напряжение, которое появляется в цепи
$$ V \: \: = \: \: V_ {1} \: \: + \: \: V_ {2} \: \: + \: \: V_ {3} $$
Где V 1 - это падение напряжения на 1- й катушке индуктивности, V 2 - это падение напряжения на 2- й катушке индуктивности, а V 3 - это падение напряжения на 3- й катушке индуктивности в вышеуказанной сети.
ток
Общее количество тока, протекающего через набор последовательно соединенных катушек индуктивности, одинаково во всех точках сети.
Ток через сеть
$$ I \: \: = \: \: I_ {1} \: \: = \: \: I_ {2} \: \: = \: \: I_ {3} $$
Где I 1 - ток через 1- ю катушку индуктивности, I 2 - это ток через 2- ю катушку индуктивности, а I 3 - это ток через 3- ю катушку индуктивности в вышеупомянутой сети.
Катушки индуктивности параллельно
Давайте посмотрим, что происходит, когда несколько резисторов подключены параллельно. Рассмотрим три резистора с разными номиналами, как показано на рисунке ниже.

Индуктивность
Полная индуктивность цепи с параллельными резисторами рассчитывается иначе, чем при использовании метода последовательной индуктивной сети. Здесь обратное (1 / R) значение индивидуальных индуктивностей складывается с обратной алгебраической суммой, чтобы получить общее значение индуктивности.
Общее значение индуктивности сети составляет
$$ \ frac {1} {L_ {T}} \: \: = \: \: \ frac {1} {L_ {1}} \: \: + \: \: \ frac {1} {L_ { 2}} \: \: + \: \: \ frac {1} {L_ {3}} $$
Где L 1 - это индуктивность 1- го индуктора, L 2 - это индуктивность 2- го индуктора, а L 3 - индуктивность 3- го индуктора в вышеуказанной сети.
Из имеющегося у нас метода вычисления параллельной индуктивности мы можем вывести простое уравнение для параллельной сети с двумя индукторами. это
$$ L_ {T} \: \: = \: \: \ frac {L_ {1} \: \: \ times \: \: L_ {2}} {L_ {1} \: \: + \: \ : L_ {2}} $$
вольтаж
Общее напряжение, которое появляется в сети параллельных индукторов, такое же, как падение напряжения на каждой отдельной индуктивности.
Напряжение, которое появляется в цепи
$$ V \: \: = \: \: V_ {1} \: \: = \: \: V_ {2} \: \: = \: \: V_ {3} $$
Где V 1 - это падение напряжения на 1- й катушке индуктивности, V 2 - это падение напряжения на 2- й катушке индуктивности, а V 3 - это падение напряжения на 3- й катушке индуктивности в вышеуказанной сети. Следовательно, напряжение одинаково во всех точках параллельной сети индукторов.
ток
Общая величина тока, поступающего в параллельную индуктивную сеть, представляет собой сумму всех отдельных токов, протекающих во всех параллельных ветвях. Величина индуктивности каждой ветви определяет величину тока, протекающего через нее.
Общий ток через сеть составляет
$$ I \: \: = \: \: I_ {1} \: \: + \: \: I_ {2} \: \: + \: \: I_ {3} $$
Где I 1 - ток через 1- ю катушку индуктивности, I 2 - это ток через 2- ю катушку индуктивности, а I 3 - это ток через 3- ю катушку индуктивности в вышеупомянутой сети.
Следовательно, сумма отдельных токов в разных ветвях дает общий ток в параллельной сети.
Индуктивное реактивное сопротивление
Индуктивное реактивное сопротивление - это сопротивление, предлагаемое индуктором потоку переменного тока, или просто переменного тока. Катушка индуктивности имеет свойство сопротивляться изменению потока тока и, следовательно, проявляет некоторую оппозицию, которую можно назватьreactance, так как частота входного тока также должна учитываться вместе с сопротивлением, которое он предлагает.
Индикация - XL
Единицы - Ohms
Символ - Ω
В чисто индуктивной цепи ток IL lagsприложенное напряжение на 90 °. Индуктивное реактивное сопротивление рассчитывается по формуле
$$ X_ {L} \: \: = \: \: 2 \ pi fL $$
Где f - частота сигнала. Следовательно, индуктивное реактивное сопротивление зависит от частоты и индуктивности.