Структуры данных - асимптотический анализ

Асимптотический анализ алгоритма относится к определению математических границ / рамок его производительности во время выполнения. Используя асимптотический анализ, мы можем очень хорошо сделать вывод о наилучшем, среднем и наихудшем сценариях алгоритма.

Асимптотический анализ - это входная граница, т. Е. Если нет входных данных для алгоритма, считается, что он работает в постоянное время. Все остальные факторы, кроме «входа», считаются постоянными.

Асимптотический анализ относится к вычислению времени выполнения любой операции в математических единицах вычисления. Например, время выполнения одной операции вычисляется как f (n), а для другой операции оно может быть вычислено как g (n ² ). Это означает, что время работы первой операции будет линейно увеличиваться с увеличениемn и время выполнения второй операции будет экспоненциально увеличиваться, когда nувеличивается. Точно так же время выполнения обеих операций будет примерно одинаковым, еслиn значительно мала.

Обычно время, необходимое алгоритму, подпадает под три типа:

Best Case - Минимальное время, необходимое для выполнения программы.
Average Case - Среднее время, необходимое для выполнения программы.
Worst Case - Максимальное время, необходимое для выполнения программы.

Асимптотические обозначения

Ниже приведены обычно используемые асимптотические обозначения для вычисления временной сложности алгоритма.

Ο Обозначение
Ω Обозначение
θ Обозначение

Нотация Big Oh, Ο

Обозначение Ο (n) - это формальный способ выразить верхнюю границу времени работы алгоритма. Он измеряет временную сложность наихудшего случая или максимальное время, которое может потребоваться для выполнения алгоритма.

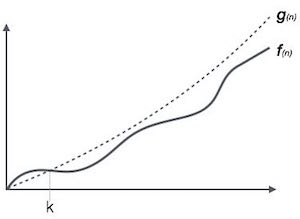
Например, для функции f(n)

Ο(f(n)) = { g(n) : there exists c > 0 and n₀ such that f(n) ≤ c.g(n) for all n > n₀. }

Омега-обозначение, Ω

Обозначение Ω (n) - это формальный способ выразить нижнюю границу времени работы алгоритма. Он измеряет наилучшую временную сложность случая или наилучшее время, которое может занять алгоритм.

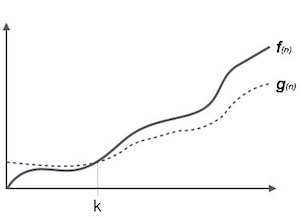
Например, для функции f(n)

Ω(f(n)) ≥ { g(n) : there exists c > 0 and n₀ such that g(n) ≤ c.f(n) for all n > n₀. }

Обозначение тета, θ

Обозначение θ (n) - это формальный способ выразить как нижнюю, так и верхнюю границу времени работы алгоритма. Он представлен следующим образом -

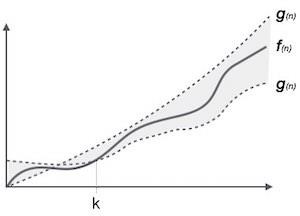
θ(f(n)) = { g(n) if and only if g(n) =  Ο(f(n)) and g(n) = Ω(f(n)) for all n > n₀. }

Общие асимптотические обозначения

Ниже приводится список некоторых распространенных асимптотических обозначений -

постоянный	-	Ο (1)
логарифмический	-	Ο (журнал n)
линейный	-	Ο (п)
п войти п	-	Ο (п войти п)
квадратичный	-	Ο (п ² )
кубический	-	Ο (п ³ )
многочлен	-	п ⁽¹⁾
экспоненциальный	-	2 ^{Ο (п)}