Структуры данных кучи

Куча - это особый случай сбалансированной структуры данных двоичного дерева, в которой ключ корневого узла сравнивается со своими дочерними элементами и размещается соответствующим образом. Еслиα имеет дочерний узел β тогда -

ключ (α) ≥ ключ (β)

Поскольку значение parent больше, чем значение child, это свойство генерирует Max Heap. Исходя из этого критерия, куча может быть двух типов:

For Input → 35 33 42 10 14 19 27 44 26 31

Min-Heap - Если значение корневого узла меньше или равно любому из его дочерних узлов.

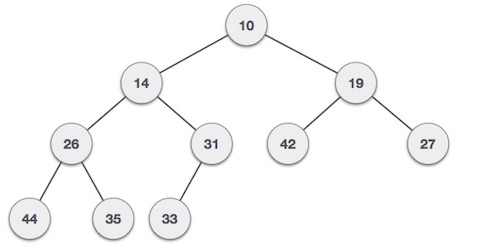
Max-Heap - Если значение корневого узла больше или равно любому из его дочерних узлов.

Оба дерева построены с использованием одних и тех же входных данных и порядка поступления.

Алгоритм построения максимальной кучи

Мы будем использовать тот же пример, чтобы продемонстрировать, как создается Max Heap. Процедура создания Min Heap аналогична, но мы используем минимальные значения вместо максимальных значений.

Мы собираемся получить алгоритм для максимальной кучи, вставляя по одному элементу за раз. В любой момент куча должна сохранять свое свойство. Во время вставки мы также предполагаем, что вставляем узел в уже сложенное дерево.

Step 1 − Create a new node at the end of heap.
Step 2 − Assign new value to the node.
Step 3 − Compare the value of this child node with its parent.
Step 4 − If value of parent is less than child, then swap them.
Step 5 − Repeat step 3 & 4 until Heap property holds.

Note - В алгоритме построения Min Heap мы ожидаем, что значение родительского узла будет меньше, чем значение дочернего узла.

Давайте разберемся с построением Max Heap с помощью анимированной иллюстрации. Мы рассматриваем ту же входную выборку, которую использовали ранее.

Максимальный алгоритм удаления кучи

Давайте выведем алгоритм удаления из максимальной кучи. Удаление в максимальной (или минимальной) куче всегда происходит в корне, чтобы удалить максимальное (или минимальное) значение.

Step 1 − Remove root node.
Step 2 − Move the last element of last level to root.
Step 3 − Compare the value of this child node with its parent.
Step 4 − If value of parent is less than child, then swap them.
Step 5 − Repeat step 3 & 4 until Heap property holds.