Глубокое обучение с Keras - Краткое руководство

В последние дни глубокое обучение стало модным словом в области искусственного интеллекта (ИИ). В течение многих лет мы использовали машинное обучение (ML) для передачи интеллекта машинам. В последние дни глубокое обучение стало более популярным из-за его превосходства в прогнозировании по сравнению с традиционными методами машинного обучения.

Глубокое обучение по сути означает обучение искусственной нейронной сети (ИНС) с огромным объемом данных. При глубоком обучении сеть обучается сама по себе, и поэтому для обучения требуются огромные данные. В то время как традиционное машинное обучение - это, по сути, набор алгоритмов, которые анализируют данные и учатся на них. Затем они использовали это обучение для принятия разумных решений.

Теперь, когда речь идет о Керасе, это высокоуровневый API нейронных сетей, который работает поверх TensorFlow - сквозной платформы машинного обучения с открытым исходным кодом. Используя Keras, вы легко определяете сложные архитектуры ИНС для экспериментов с вашими большими данными. Keras также поддерживает графический процессор, который становится необходимым для обработки огромного количества данных и разработки моделей машинного обучения.

В этом руководстве вы узнаете, как использовать Keras для построения глубоких нейронных сетей. Мы рассмотрим практические примеры для обучения. Проблема заключается в распознавании рукописных цифр с помощью нейронной сети, обученной с помощью глубокого обучения.

Чтобы вас больше заинтересовало глубокое обучение, ниже приведен снимок экрана с тенденциями Google в области глубокого обучения.

Как видно из диаграммы, интерес к глубокому обучению неуклонно растет в последние несколько лет. Существует множество областей, таких как компьютерное зрение, обработка естественного языка, распознавание речи, биоинформатика, разработка лекарств и т. Д., Где глубокое обучение было успешно применено. Это руководство поможет вам быстро приступить к глубокому обучению.

Так что продолжайте читать!

Как сказано во введении, глубокое обучение - это процесс обучения искусственной нейронной сети с огромным объемом данных. После обучения сеть сможет давать нам прогнозы на основе невидимых данных. Прежде чем я продолжу объяснять, что такое глубокое обучение, давайте быстро рассмотрим некоторые термины, используемые при обучении нейронной сети.

Нейронные сети

Идея искусственной нейронной сети возникла из нейронных сетей в нашем мозгу. Типичная нейронная сеть состоит из трех слоев - входного, выходного и скрытого, как показано на рисунке ниже.

Это также называется shallowнейронная сеть, так как содержит только один скрытый слой. Вы добавляете больше скрытых слоев в вышеупомянутую архитектуру, чтобы создать более сложную архитектуру.

Глубокие сети

На следующей диаграмме показана глубокая сеть, состоящая из четырех скрытых слоев, входного слоя и выходного слоя.

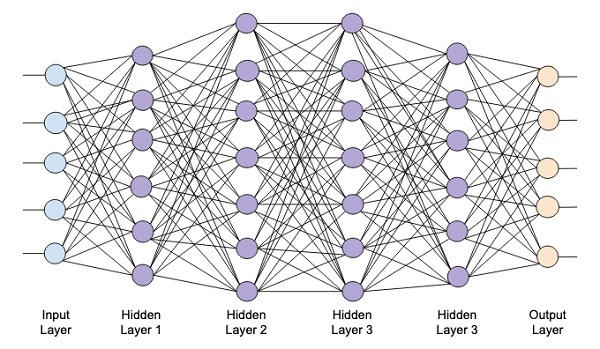
По мере добавления к сети количества скрытых слоев ее обучение становится более сложным с точки зрения требуемых ресурсов и времени, необходимого для полного обучения сети.

Сетевое обучение

После определения сетевой архитектуры вы обучаете ее делать определенные виды прогнозов. Обучение сети - это процесс определения правильных весов для каждого звена в сети. Во время обучения данные перетекают от входных к выходным слоям через различные скрытые слои. Поскольку данные всегда движутся в одном направлении от входа к выходу, мы называем эту сеть прямой сетью, а распространение данных - прямым распространением.

Функция активации

На каждом уровне мы вычисляем взвешенную сумму входов и передаем ее в функцию активации. Функция активации привносит в сеть нелинейность. Это просто математическая функция, дискретизирующая вывод. Некоторые из наиболее часто используемых функций активации - сигмовидная, гиперболическая, касательная (tanh), ReLU и Softmax.

Обратное распространение

Обратное распространение - это алгоритм контролируемого обучения. При обратном распространении ошибки распространяются в обратном направлении от выходного уровня к входному. Для данной функции ошибок мы вычисляем градиент функции ошибок относительно весов, присвоенных каждому соединению. Расчет градиента выполняется в обратном направлении по сети. Градиент последнего слоя весов вычисляется первым, а градиент первого слоя весов вычисляется последним.

На каждом слое частичные вычисления градиента повторно используются при вычислении градиента для предыдущего слоя. Это называется градиентным спуском.

В этом учебном пособии, основанном на проектах, вы определите глубокую нейронную сеть с прямой связью и обучите ее методам обратного распространения ошибки и градиентного спуска. К счастью, Keras предоставляет всем нам высокоуровневые API для определения сетевой архитектуры и обучения ее с помощью градиентного спуска. Далее вы узнаете, как это сделать в Керасе.

Система распознавания рукописных цифр

В этом мини-проекте вы будете применять методы, описанные ранее. Вы создадите нейронную сеть с глубоким обучением, которая будет обучена распознавать рукописные цифры. В любом проекте машинного обучения первая проблема - это сбор данных. В частности, для сетей глубокого обучения вам нужны огромные данные. К счастью, для проблемы, которую мы пытаемся решить, кто-то уже создал набор данных для обучения. Это называется mnist, который доступен как часть библиотек Keras. Набор данных состоит из нескольких изображений рукописных цифр размером 28x28 пикселей. Вы обучите свою модель основной части этого набора данных, а остальные данные будут использоваться для проверки вашей обученной модели.

Описание Проекта

В mnistнабор данных состоит из 70000 изображений рукописных цифр. Здесь для справки воспроизведены несколько образцов изображений.

Каждое изображение имеет размер 28 x 28 пикселей, что в сумме составляет 768 пикселей с различными уровнями шкалы серого. Большинство пикселей имеют тенденцию к черному оттенку, в то время как лишь некоторые из них имеют тенденцию к белому. Мы поместим распределение этих пикселей в массив или вектор. Например, распределение пикселей для типичного изображения цифр 4 и 5 показано на рисунке ниже.

Каждое изображение имеет размер 28 x 28 пикселей, что в сумме составляет 768 пикселей с различными уровнями шкалы серого. Большинство пикселей имеют тенденцию к черному оттенку, в то время как лишь некоторые из них имеют тенденцию к белому. Мы поместим распределение этих пикселей в массив или вектор. Например, распределение пикселей для типичного изображения цифр 4 и 5 показано на рисунке ниже.

Ясно, что вы можете видеть, что распределение пикселей (особенно тех, которые имеют тенденцию к белому тону) различаются, это отличает цифры, которые они представляют. Мы передадим это распределение 784 пикселей в нашу сеть в качестве входных данных. Выходные данные сети будут состоять из 10 категорий, представляющих цифру от 0 до 9.

Наша сеть будет состоять из 4 слоев - одного входного, одного выходного и двух скрытых слоев. Каждый скрытый слой будет содержать 512 узлов. Каждый слой полностью связан со следующим слоем. Когда мы обучаем сеть, мы будем вычислять веса для каждого соединения. Мы обучаем сеть, применяя обратное распространение и градиентный спуск, которые мы обсуждали ранее.

На этом фоне давайте приступим к созданию проекта.

Настройка проекта

Мы будем использовать Jupyter через Anacondaнавигатор для нашего проекта. Поскольку в нашем проекте используются TensorFlow и Keras, вам нужно будет установить их в программе установки Anaconda. Чтобы установить Tensorflow, выполните следующую команду в окне консоли:

>conda install -c anaconda tensorflow

Чтобы установить Keras, используйте следующую команду -

>conda install -c anaconda keras

Теперь вы готовы запустить Jupyter.

Запуск Jupyter

Когда вы запустите навигатор Anaconda, вы увидите следующий начальный экран.

Нажмите ‘Jupyter’чтобы запустить это. На экране отобразятся существующие проекты, если таковые имеются, на вашем диске.

Запуск нового проекта

Запустите новый проект Python 3 в Anaconda, выбрав следующий параметр меню -

File | New Notebook | Python 3

Снимок экрана выбора меню показан для вашего быстрого ознакомления -

На вашем экране появится новый пустой проект, как показано ниже -

Измените название проекта на DeepLearningDigitRecognition нажав и отредактировав имя по умолчанию “UntitledXX”.

Сначала мы импортируем различные библиотеки, необходимые для кода в нашем проекте.

Обработка массивов и построение графиков

Как правило, мы используем numpy для обработки массивов и matplotlibдля черчения. Эти библиотеки импортируются в наш проект с использованием следующихimport заявления

import numpy as np
import matplotlib
import matplotlib.pyplot as plot

Подавление предупреждений

Поскольку и Tensorflow, и Keras продолжают пересматривать, если вы не синхронизируете их соответствующие версии в проекте, во время выполнения вы увидите множество предупреждающих ошибок. Поскольку они отвлекают ваше внимание от обучения, мы будем подавлять все предупреждения в этом проекте. Это делается с помощью следующих строк кода -

# silent all warnings
import os
os.environ['TF_CPP_MIN_LOG_LEVEL']='3'
import warnings
warnings.filterwarnings('ignore')
from tensorflow.python.util import deprecation
deprecation._PRINT_DEPRECATION_WARNINGS = False

Керас

Мы используем библиотеки Keras для импорта набора данных. Мы будем использоватьmnistнабор данных для рукописных цифр. Мы импортируем необходимый пакет, используя следующую инструкцию

from keras.datasets import mnist

Мы будем определять нашу нейронную сеть глубокого обучения с помощью пакетов Keras. Мы импортируемSequential, Dense, Dropout а также Activationпакеты для определения сетевой архитектуры. Мы используемload_modelпакет для сохранения и извлечения нашей модели. Мы также используемnp_utilsдля нескольких утилит, которые нам нужны в нашем проекте. Этот импорт выполняется с помощью следующих программных операторов -

from keras.models import Sequential, load_model
from keras.layers.core import Dense, Dropout, Activation
from keras.utils import np_utils

Когда вы запустите этот код, вы увидите сообщение на консоли, в котором говорится, что Keras использует TensorFlow на бэкэнде. Скриншот на этом этапе показан здесь -

Теперь, когда у нас есть весь импорт, необходимый для нашего проекта, мы приступим к определению архитектуры нашей сети глубокого обучения.

Наша модель нейронной сети будет состоять из линейного стека слоев. Чтобы определить такую ​​модель, мы называемSequential функция -

model = Sequential()

Входной слой

Мы определяем входной уровень, который является первым уровнем в нашей сети, используя следующий оператор программы:

model.add(Dense(512, input_shape=(784,)))

Это создает слой с 512 узлами (нейронами) с 784 входными узлами. Это изображено на рисунке ниже -

Обратите внимание, что все входные узлы полностью подключены к уровню 1, то есть каждый входной узел подключен ко всем 512 узлам уровня 1.

Затем нам нужно добавить функцию активации для вывода уровня 1. Мы будем использовать ReLU в качестве нашей активации. Функция активации добавляется с помощью следующего программного оператора -

model.add(Activation('relu'))

Затем мы добавляем Dropout 20%, используя приведенную ниже инструкцию. Отбрасывание - это метод, используемый для предотвращения переобучения модели.

model.add(Dropout(0.2))

На этом этапе наш входной слой полностью определен. Далее мы добавим скрытый слой.

Скрытый слой

Наш скрытый слой будет состоять из 512 узлов. Вход в скрытый слой поступает из нашего ранее определенного входного слоя. Все узлы полностью подключены, как и в предыдущем случае. Вывод скрытого слоя перейдет к следующему слою в сети, который будет нашим последним и выходным слоем. Мы будем использовать ту же активацию ReLU, что и для предыдущего слоя, с пропуском 20%. Код для добавления этого слоя приведен здесь -

model.add(Dense(512))
model.add(Activation('relu'))
model.add(Dropout(0.2))

Сеть на этом этапе можно визуализировать следующим образом -

Затем мы добавим в нашу сеть последний слой, который является выходным слоем. Обратите внимание, что вы можете добавить любое количество скрытых слоев, используя код, аналогичный тому, который вы использовали здесь. Добавление большего количества слоев сделало бы сеть сложной для обучения; тем не менее, дает определенное преимущество в виде лучших результатов во многих случаях, хотя и не во всех.

Выходной слой

Выходной слой состоит всего из 10 узлов, так как мы хотим классифицировать данные изображения по 10 различным цифрам. Мы добавляем этот слой, используя следующую инструкцию -

model.add(Dense(10))

Поскольку мы хотим разделить вывод на 10 отдельных единиц, мы используем активацию softmax. В случае ReLU вывод двоичный. Мы добавляем активацию, используя следующий оператор -

model.add(Activation('softmax'))

На этом этапе нашу сеть можно визуализировать, как показано на диаграмме ниже -

На данный момент наша сетевая модель полностью определена в программном обеспечении. Запустите ячейку кода, и если ошибок нет, вы получите подтверждающее сообщение на экране, как показано на скриншоте ниже -

Далее нам нужно скомпилировать модель.

Компиляция выполняется с использованием одного вызова метода, называемого compile.

model.compile(loss='categorical_crossentropy', metrics=['accuracy'], optimizer='adam')

В compileМетод требует нескольких параметров. Параметр потерь указывается иметь тип'categorical_crossentropy'. Параметр метрики установлен на'accuracy' и, наконец, мы используем adamоптимизатор для обучения сети. Результат на этом этапе показан ниже -

Теперь мы готовы передать данные в нашу сеть.

Загрузка данных

Как было сказано ранее, мы будем использовать mnistнабор данных предоставлен Керасом. Когда мы загружаем данные в нашу систему, мы разделим их на обучающие и тестовые данные. Данные загружаются путем вызоваload_data метод следующим образом -

(X_train, y_train), (X_test, y_test) = mnist.load_data()

Результат на этом этапе выглядит следующим образом -

Теперь мы изучим структуру загруженного набора данных.

Предоставляемые нам данные представляют собой графические изображения размером 28 x 28 пикселей, каждое из которых содержит одну цифру от 0 до 9. Мы отобразим первые десять изображений на консоли. Код для этого приведен ниже -

# printing first 10 images
for i in range(10):

plot.subplot(3,5,i+1)
plot.tight_layout()
plot.imshow(X_train[i], cmap='gray', interpolation='none')
plot.title("Digit: {}".format(y_train[i]))
plot.xticks([])
plot.yticks([])

В итеративном цикле из 10 отсчетов мы создаем подзаголовок на каждой итерации и показываем изображение из X_trainвектор в нем. Назовем каждое изображение из соответствующегоy_trainвектор. Обратите внимание, чтоy_train вектор содержит фактические значения для соответствующего изображения в X_trainвектор. Мы удаляем маркировку осей x и y, вызывая два методаxticks а также yticksс нулевым аргументом. Когда вы запустите код, вы увидите следующий результат -

Далее мы подготовим данные для подачи их в нашу сеть.

Прежде чем передавать данные в нашу сеть, они должны быть преобразованы в формат, необходимый для сети. Это называется подготовкой данных для сети. Обычно он состоит из преобразования многомерного ввода в одномерный вектор и нормализации точек данных.

Изменение формы входного вектора

Изображения в нашем наборе данных состоят из 28 x 28 пикселей. Его нужно преобразовать в одномерный вектор размером 28 * 28 = 784 для подачи его в нашу сеть. Мы делаем это, вызываяreshape метод на векторе.

X_train = X_train.reshape(60000, 784)
X_test = X_test.reshape(10000, 784)

Теперь наш обучающий вектор будет состоять из 60000 точек данных, каждая из которых состоит из одномерного вектора размером 784. Точно так же наш тестовый вектор будет состоять из 10000 точек данных одномерного вектора размера 784.

Нормализация данных

Данные, которые содержит входной вектор, в настоящее время имеют дискретное значение от 0 до 255 - уровни серой шкалы. Нормализация этих значений пикселей между 0 и 1 помогает ускорить обучение. Поскольку мы собираемся использовать стохастический градиентный спуск, нормализация данных также поможет снизить вероятность застревания в локальных оптимумах.

Чтобы нормализовать данные, мы представляем их как тип с плавающей запятой и делим на 255, как показано в следующем фрагменте кода:

X_train = X_train.astype('float32')
X_test = X_test.astype('float32')
X_train /= 255
X_test /= 255

Давайте теперь посмотрим, как выглядят нормализованные данные.

Изучение нормализованных данных

Чтобы просмотреть нормализованные данные, мы вызовем функцию гистограммы, как показано здесь -

plot.hist(X_train[0])
plot.title("Digit: {}".format(y_train[0]))

Здесь мы строим гистограмму первого элемента X_trainвектор. Мы также печатаем цифру, представленную этой точкой данных. Результат выполнения вышеуказанного кода показан здесь -

Вы заметите плотную плотность точек со значением, близким к нулю. Это черные точки на изображении, которые, очевидно, составляют основную часть изображения. Остальные точки серой шкалы, близкие к белому, представляют цифру. Вы можете проверить распределение пикселей для другой цифры. Приведенный ниже код печатает гистограмму цифры с индексом 2 в наборе обучающих данных.

plot.hist(X_train[2])
plot.title("Digit: {}".format(y_train[2])

Результат выполнения вышеуказанного кода показан ниже -

Сравнивая два приведенных выше рисунка, вы заметите, что распределение белых пикселей на двух изображениях отличается, что указывает на представление другой цифры - «5» и «4» на двух приведенных выше изображениях.

Затем мы рассмотрим распределение данных в нашем полном наборе обучающих данных.

Изучение распределения данных

Прежде чем обучать нашу модель машинного обучения на нашем наборе данных, мы должны знать распределение уникальных цифр в нашем наборе данных. Наши изображения представляют собой 10 различных цифр в диапазоне от 0 до 9. Мы хотели бы знать количество цифр 0, 1 и т. Д. В нашем наборе данных. Мы можем получить эту информацию, используяunique метод Numpy.

Используйте следующую команду, чтобы напечатать количество уникальных значений и количество вхождений каждого из них.

print(np.unique(y_train, return_counts=True))

Когда вы запустите указанную выше команду, вы увидите следующий вывод -

(array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9], dtype=uint8), array([5923, 6742, 5958, 6131, 5842, 5421, 5918, 6265, 5851, 5949]))

Он показывает, что существует 10 различных значений - от 0 до 9. Имеется 5923 появления цифры 0, 6742 появления цифры 1 и т. Д. Снимок экрана вывода показан здесь -

На последнем этапе подготовки данных нам нужно закодировать наши данные.

Кодирование данных

В нашем наборе данных есть десять категорий. Таким образом, мы будем кодировать наш вывод в этих десяти категориях, используя однократное кодирование. Мы используем метод to_categorial утилит Numpy для выполнения кодирования. После кодирования выходных данных каждая точка данных будет преобразована в одномерный вектор размера 10. Например, цифра 5 теперь будет представлена ​​как [0,0,0,0,0,1,0,0,0 , 0].

Закодируйте данные, используя следующий фрагмент кода -

n_classes = 10
Y_train = np_utils.to_categorical(y_train, n_classes)

Вы можете проверить результат кодирования, распечатав первые 5 элементов категоризированного вектора Y_train.

Используйте следующий код для печати первых 5 векторов -

for i in range(5):
   print (Y_train[i])

Вы увидите следующий вывод -

[0. 0. 0. 0. 0. 1. 0. 0. 0. 0.]
[1. 0. 0. 0. 0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 1. 0. 0. 0. 0. 0.]
[0. 1. 0. 0. 0. 0. 0. 0. 0. 0.]
[0. 0. 0. 0. 0. 0. 0. 0. 0. 1.]

Первый элемент представляет собой цифру 5, второй - цифру 0 и так далее.

Наконец, вам также придется классифицировать тестовые данные, что делается с помощью следующего оператора:

Y_test = np_utils.to_categorical(y_test, n_classes)

На этом этапе ваши данные полностью подготовлены для передачи в сеть.

Далее идет самая важная часть - обучение нашей сетевой модели.

Обучение модели выполняется одним вызовом метода под названием fit, который принимает несколько параметров, как показано в приведенном ниже коде:

history = model.fit(X_train, Y_train,
   batch_size=128, epochs=20,
   verbose=2,
   validation_data=(X_test, Y_test)))

Первые два параметра метода подгонки определяют функции и выходные данные обучающего набора данных.

В epochsустановлено на 20; мы предполагаем, что обучение сойдется максимум за 20 эпох - итераций. Обученная модель проверяется на тестовых данных, как указано в последнем параметре.

Частичный вывод выполнения вышеуказанной команды показан здесь -

Train on 60000 samples, validate on 10000 samples
Epoch 1/20
- 9s - loss: 0.2488 - acc: 0.9252 - val_loss: 0.1059 - val_acc: 0.9665
Epoch 2/20
- 9s - loss: 0.1004 - acc: 0.9688 - val_loss: 0.0850 - val_acc: 0.9715
Epoch 3/20
- 9s - loss: 0.0723 - acc: 0.9773 - val_loss: 0.0717 - val_acc: 0.9765
Epoch 4/20
- 9s - loss: 0.0532 - acc: 0.9826 - val_loss: 0.0665 - val_acc: 0.9795
Epoch 5/20
- 9s - loss: 0.0457 - acc: 0.9856 - val_loss: 0.0695 - val_acc: 0.9792

Снимок экрана вывода приведен ниже для вашего быстрого ознакомления -

Теперь, когда модель обучена на наших обучающих данных, мы оценим ее производительность.

Чтобы оценить производительность модели, мы вызываем evaluate метод следующим образом -

loss_and_metrics = model.evaluate(X_test, Y_test, verbose=2)

Чтобы оценить производительность модели, мы вызываем evaluate метод следующим образом -

loss_and_metrics = model.evaluate(X_test, Y_test, verbose=2)

Мы напечатаем потерю и точность, используя следующие два утверждения:

print("Test Loss", loss_and_metrics[0])
print("Test Accuracy", loss_and_metrics[1])

Когда вы запустите вышеуказанные операторы, вы увидите следующий результат -

Test Loss 0.08041584826191042
Test Accuracy 0.9837

Это показывает точность теста 98%, что должно быть приемлемо для нас. Для нас это означает, что в 2% случаев рукописные цифры не будут правильно классифицированы. Мы также построим метрики точности и потерь, чтобы увидеть, как модель работает с тестовыми данными.

Построение метрик точности

Мы используем записанные historyво время нашего обучения, чтобы получить график показателей точности. Следующий код будет отображать точность для каждой эпохи. Мы выбираем точность обучающих данных («acc») и точность данных проверки («val_acc») для построения графика.

plot.subplot(2,1,1)
plot.plot(history.history['acc'])
plot.plot(history.history['val_acc'])
plot.title('model accuracy')
plot.ylabel('accuracy')
plot.xlabel('epoch')
plot.legend(['train', 'test'], loc='lower right')

Выходной график показан ниже -

Как вы можете видеть на диаграмме, точность быстро возрастает в первые две эпохи, указывая на то, что сеть быстро обучается. После этого кривая сглаживается, указывая на то, что для дальнейшего обучения модели требуется не слишком много эпох. Обычно, если точность обучающих данных («acc») продолжает улучшаться, а точность данных проверки («val_acc») ухудшается, вы сталкиваетесь с переобучением. Это означает, что модель начинает запоминать данные.

Мы также построим метрики потерь, чтобы проверить производительность нашей модели.

Построение метрики убытков

Опять же, мы наносим потери как на обучающие («потеря»), так и на тестовые («val_loss») данные. Это делается с помощью следующего кода -

plot.subplot(2,1,2)
plot.plot(history.history['loss'])
plot.plot(history.history['val_loss'])
plot.title('model loss')
plot.ylabel('loss')
plot.xlabel('epoch')
plot.legend(['train', 'test'], loc='upper right')

Вывод этого кода показан ниже -

Как вы можете видеть на диаграмме, потери в обучающей выборке быстро уменьшаются в течение первых двух эпох. Для тестового набора потери не уменьшаются с той же скоростью, что и для обучающего набора, но остаются практически неизменными для нескольких эпох. Это означает, что наша модель хорошо обобщается на невидимые данные.

Теперь мы будем использовать нашу обученную модель для прогнозирования цифр в наших тестовых данных.

Предсказать цифры в невидимых данных очень легко. Вам просто нужно позвонить вpredict_classes метод model передав его в вектор, состоящий из ваших неизвестных точек данных.

predictions = model.predict_classes(X_test)

Вызов метода возвращает прогнозы в векторе, который можно проверить на предмет 0 и 1 относительно фактических значений. Это делается с помощью следующих двух операторов -

correct_predictions = np.nonzero(predictions == y_test)[0]
incorrect_predictions = np.nonzero(predictions != y_test)[0]

Наконец, мы напечатаем количество правильных и неправильных прогнозов, используя следующие два программного оператора:

print(len(correct_predictions)," classified correctly")
print(len(incorrect_predictions)," classified incorrectly")

Когда вы запустите код, вы получите следующий результат -

9837 classified correctly
163 classified incorrectly

Теперь, когда вы успешно обучили модель, мы сохраним ее для использования в будущем.

Мы сохраним обученную модель на нашем локальном диске в папке моделей в нашем текущем рабочем каталоге. Чтобы сохранить модель, запустите следующий код -

directory = "./models/"
name = 'handwrittendigitrecognition.h5'
path = os.path.join(save_dir, name)
model.save(path)
print('Saved trained model at %s ' % path)

Результат после запуска кода показан ниже -

Теперь, когда вы сохранили обученную модель, вы можете использовать ее позже для обработки неизвестных данных.

Чтобы предсказать невидимые данные, вам сначала нужно загрузить обученную модель в память. Это делается с помощью следующей команды -

model = load_model ('./models/handwrittendigitrecognition.h5')

Обратите внимание, что мы просто загружаем файл .h5 в память. Это устанавливает всю нейронную сеть в памяти вместе с весами, назначенными каждому слою.

Теперь, чтобы делать свои прогнозы на невидимых данных, загрузите данные, пусть это будет один или несколько элементов, в память. Предварительно обработайте данные, чтобы они соответствовали входным требованиям нашей модели, как то, что вы делали с данными обучения и тестирования выше. После предварительной обработки загрузите его в свою сеть. Модель выдаст свой прогноз.

Keras предоставляет API высокого уровня для создания глубокой нейронной сети. В этом руководстве вы научились создавать глубокую нейронную сеть, которая была обучена обнаружению цифр в рукописном тексте. Для этого была создана многоуровневая сеть. Keras позволяет вам определять функцию активации по вашему выбору на каждом уровне. Используя градиентный спуск, сеть обучалась на обучающих данных. Точность обученной сети в предсказании невидимых данных была проверена на тестовых данных. Вы научились строить метрики точности и погрешности. После того, как сеть полностью обучена, вы сохранили модель сети для будущего использования.