Электронные схемы - формирование линейных волн

Сигнал также можно назвать Wave. Каждая волна имеет определенную форму, когда она представлена ​​на графике. Эта форма может быть разных типов, таких как синусоидальная, квадратная, треугольная и т. Д., Которые меняются в зависимости от периода времени, или они могут иметь некоторые случайные формы без учета периода времени.

Типы формирования волны

Есть два основных типа формирования волн. Они -

• Формирование линейной волны
• Нелинейное формирование волны

Формирование линейной волны

Линейные элементы, такие как резисторы, конденсаторы и катушки индуктивности, используются для формирования сигнала при таком линейном формировании волны. Входной сигнал синусоидальной волны имеет выходной сигнал синусоидальной формы, и поэтому несинусоидальные входы чаще используются для понимания линейного формирования волны.

Filtering представляет собой процесс ослабления нежелательного сигнала или воспроизведения выбранных частей частотных составляющих конкретного сигнала.

Фильтры

Если в процессе формирования сигнала некоторые части сигнала кажутся нежелательными, их можно отсечь с помощью схемы фильтра. A Filter is a circuit that can remove unwanted portions of a signal at its input. Процесс уменьшения силы сигнала также называютAttenuation.

У нас есть несколько компонентов, которые помогают нам в методах фильтрации.

• А Capacitor имеет свойство allow AC и чтобы block DC

• An Inductor имеет свойство allow DC но blocks AC.

Используя эти свойства, эти два компонента особенно используются для блокировки или разрешения AC или же DC. Фильтры могут быть разработаны в зависимости от этих свойств.

У нас есть четыре основных типа фильтров -

• Фильтр низких частот
• Фильтр высоких частот
• Полосовой фильтр
• Полосовой стоп-фильтр

Давайте теперь обсудим эти типы фильтров подробно.

Фильтр низких частот

Схема фильтра, которая допускает набор частот ниже указанного значения, может быть названа Low pass filter. Этот фильтр пропускает нижние частоты. Принципиальная схема фильтра нижних частот с использованием RC и RL показана ниже.

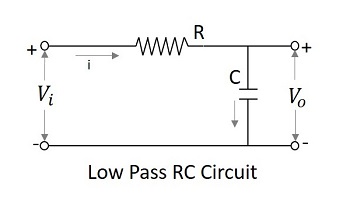
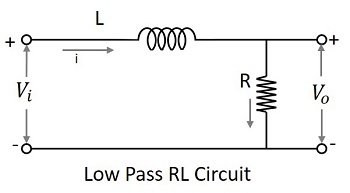
Конденсаторный фильтр или RC фильтр и индуктивный фильтр или фильтр RL оба действуют как фильтры нижних частот.

• The RC filter- Поскольку конденсатор подключен к шунту, переменный ток, который он допускает, заземляется. Это пропускает все высокочастотные компоненты, в то время как на выходе остается постоянный ток.

• The RL filter- Поскольку катушка индуктивности включена последовательно, на выходе допускается постоянный ток. Индуктор блокирует переменный ток, недопустимый на выходе.

Символ фильтра низких частот (ФНЧ) приведен ниже.

Частотный отклик

Частотная характеристика практического фильтра показана ниже, а частотная характеристика идеального фильтра нижних частот, когда не учитываются практические аспекты электронных компонентов, будет следующей.

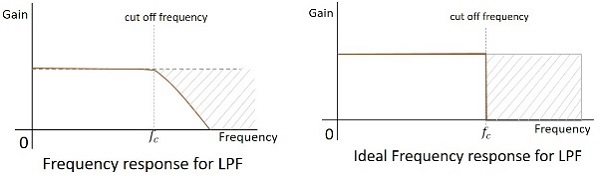
Частота среза для любого фильтра - это критическая частота $ f_ {c} $, для которой фильтр предназначен для ослабления (отсечения) сигнала. Идеальный фильтр имеет идеальную отсечку, тогда как практический имеет несколько ограничений.

Фильтр RLC

Зная о фильтрах RC и RL, можно подумать, что было бы неплохо добавить эти две цепи, чтобы получить лучший отклик. На следующем рисунке показано, как выглядит схема RLC.

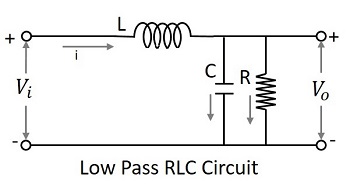
Сигнал на входе проходит через индуктор, который блокирует переменный ток и допускает постоянный ток. Теперь этот выход снова проходит через конденсатор в шунте, который заземляет оставшуюся составляющую переменного тока, если таковая имеется, присутствует в сигнале, позволяя постоянному току на выходе. Таким образом, мы имеем на выходе чистый DC. Это лучшая схема нижних частот, чем они оба.

Фильтр высоких частот

Схема фильтра, которая допускает набор частот, которые above a specified value можно назвать High pass filter. Этот фильтр пропускает более высокие частоты. Принципиальная схема фильтра высоких частот с использованием RC и RL показана ниже.

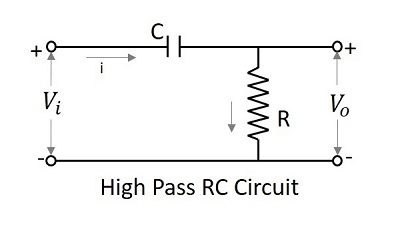
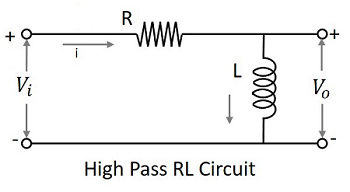
Конденсаторный фильтр или RC фильтр и фильтр индуктивности или RL оба фильтра действуют как фильтры высоких частот.

RC фильтр

Поскольку конденсатор включен последовательно, он блокирует компоненты постоянного тока и позволяет компонентам переменного тока выводиться на выход. Следовательно, высокочастотные составляющие появляются на выходе через резистор.

Фильтр RL

Поскольку катушка индуктивности помещена в шунт, допускается заземление постоянного тока. Оставшаяся составляющая переменного тока появляется на выходе. Символ фильтра высоких частот (HPF) приведен ниже.

Частотный отклик

Частотная характеристика практического фильтра показана здесь ниже, а частотная характеристика идеального HPF, когда практические аспекты электронных компонентов не принимаются во внимание, будет следующей.

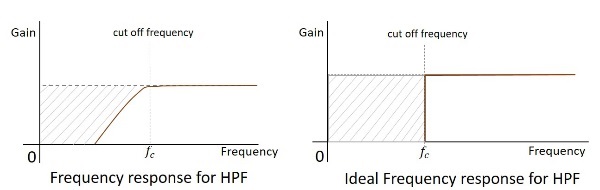
Частота среза для любого фильтра - это критическая частота $ f_ {c} $, для которой фильтр предназначен для ослабления (отсечения) сигнала. Идеальный фильтр имеет идеальную отсечку, тогда как практический имеет несколько ограничений.

Фильтр RLC

Зная о фильтрах RC и RL, можно подумать, что было бы неплохо добавить эти две цепи, чтобы получить лучший отклик. На следующем рисунке показано, как выглядит схема RLC.

Сигнал на входе проходит через конденсатор, который блокирует постоянный ток и пропускает переменный ток. Теперь этот выход снова проходит через катушку индуктивности в шунте, который заземляет оставшуюся составляющую постоянного тока, если таковая имеется, присутствует в сигнале, позволяя перем. Таким образом, мы имеем на выходе чистый переменный ток. Это лучшая схема верхних частот, чем они оба.

Полосовой фильтр

Схема фильтра, которая допускает набор частот, которые between two specified values можно назвать Band pass filter. Этот фильтр пропускает полосу частот.

Поскольку нам нужно исключить несколько низких и высоких частот, чтобы выбрать набор указанных частот, нам нужно каскадировать HPF и LPF, чтобы получить BPF. Это легко понять даже по кривым частотных характеристик.

Принципиальная схема полосового фильтра показана ниже.

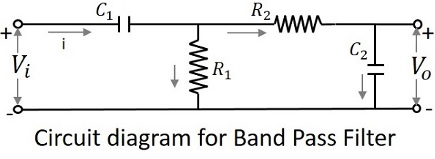
Вышеупомянутая схема также может быть построена с использованием схем RL или схем RLC. Вышеупомянутая схема RC выбрана для простоты понимания.

Символ полосового фильтра (BPF) приведен ниже.

Частотный отклик

Частотная характеристика практического фильтра показана здесь ниже, а частотная характеристика идеального BPF, когда практические соображения электронных компонентов не принимаются во внимание, будет следующей.

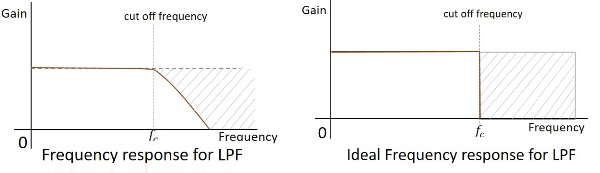
Частота среза для любого фильтра - это критическая частота $ f_ {c} $, для которой фильтр предназначен для ослабления (отсечения) сигнала. Идеальный фильтр имеет идеальную отсечку, тогда как практический имеет несколько ограничений.

Полосовой стоп-фильтр

Схема фильтра, которая блокирует или ослабляет набор частот, которые between two specified values можно назвать Band Stop filter. Этот фильтр отклоняет полосу частот и, следовательно, также может называтьсяBand Reject Filter.

Поскольку нам нужно исключить несколько низких и высоких частот, чтобы выбрать набор указанных частот, нам нужно каскадировать LPF и HPF, чтобы получить BSF. Это легко понять даже по кривым частотных характеристик.

Принципиальная схема полосового заградительного фильтра показана ниже.

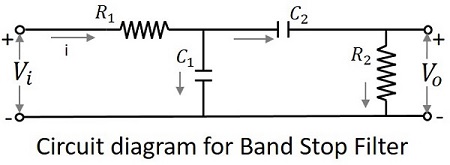
Вышеупомянутая схема также может быть построена с использованием схем RL или схем RLC. Вышеупомянутая схема RC выбрана для простоты понимания.

Символ полосового заградительного фильтра (BSF) приведен ниже.

Частотный отклик

Частотная характеристика практического фильтра показана ниже, а частотная характеристика идеального BSF, когда не учитываются практические аспекты электронных компонентов, будет следующей.

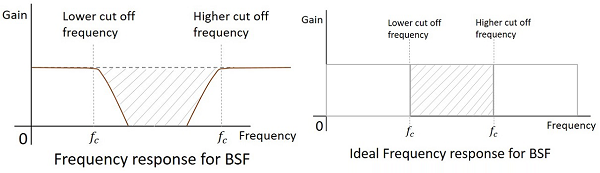
Частота среза для любого фильтра - это критическая частота $ f_ {c} $, для которой фильтр предназначен для ослабления (отсечения) сигнала. Идеальный фильтр имеет идеальную отсечку, тогда как практический имеет несколько ограничений.