Электронные схемы - сигналы
А Signalможет пониматься как «представление, которое дает некоторую информацию о данных, имеющихся в источнике, из которого они созданы». Обычно это время меняется. Следовательно, сигнал может бытьsource of energy which transmits some information. Это легко представить в виде графика.
Примеры
- Будильник подает сигнал, что пора.
- Свисток плиты подтверждает, что еда приготовлена.
- Красный свет сигнализирует об опасности.
- Светофор указывает на ваше движение.
- Звонит телефон, сигнализируя о том, что вам звонят.
Сигнал может быть любого типа, который передает некоторую информацию. Этот сигнал, создаваемый электронным оборудованием, называетсяElectronic Signal или же Electrical Signal. Обычно это временные варианты.
Типы сигналов
Сигналы можно разделить на аналоговые или цифровые, в зависимости от их характеристик. Аналоговые и цифровые сигналы можно дополнительно классифицировать, как показано на следующем рисунке.
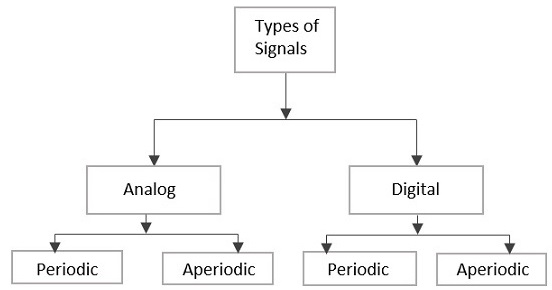
Аналоговый сигнал
Непрерывный изменяющийся во времени сигнал, который представляет собой изменяющуюся во времени величину, можно назвать Analog Signal. Этот сигнал продолжает изменяться во времени в соответствии с мгновенными значениями представляющей его величины.
Цифровой сигнал
Сигнал, который discrete в природе или который non-continuous по форме можно назвать Digital signal. Этот сигнал имеет отдельные значения, обозначенные отдельно, которые не основаны на предыдущих значениях, как если бы они были получены в этот конкретный момент времени.
Периодический сигнал и апериодический сигнал
Любой аналоговый или цифровой сигнал, который повторяет свой образец в течение определенного периода времени, называется Periodic Signal. Этот сигнал имеет повторяющуюся структуру, и его легко предположить или рассчитать.
Любой аналоговый или цифровой сигнал, который не повторяет свой образец в течение определенного периода времени, называется Aperiodic Signal. Этот сигнал имеет свой образец продолжения, но образец не повторяется, и его не так легко предположить или рассчитать.
Сигналы и обозначения
Среди Periodic Signals, наиболее часто используемыми сигналами являются синусоидальная волна, косинусная волна, треугольная форма волны, прямоугольная волна, прямоугольная волна, зубчатая волна, импульсная волна или последовательность импульсов и т. д. давайте взглянем на эти формы волны.
Сигнал шага устройства
Сигнал единичного шага имеет значение от одной единицы от источника до одной единицы по оси X. В основном это используется как тестовый сигнал. Изображение сигнала единичного шага показано ниже.
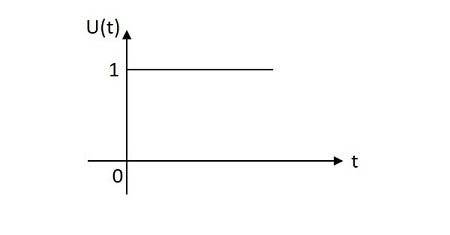
Функция единичного шага обозначается $ u \ left (t \ right) $. Это определяется как -
$$ u \ left (t \ right) = \ left \ {\ begin {matrix} 1 & t \ geq 0 \\ 0 & t <0 \ end {matrix} \ right. $$
Импульсный сигнал блока
Единичный импульсный сигнал имеет значение в одну единицу в своем источнике. Его площадь составляет одну единицу. Изображение единичного импульсного сигнала показано ниже.
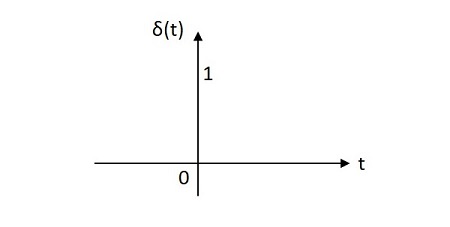
Единичная импульсная функция обозначается ẟ(t). Он определяется как
$$ \ delta \ left (t \ right) = \ left \ {\ begin {matrix} \ infty \: \: if \: \: t = 0 \\ 0 \: \: if \: \: t \ neq 0 \ end {matrix} \ right. $$
$$ \ int _ {- \ infty} ^ {\ infty} \ delta \ left (t \ right) d \ left (t \ right) = 1 $$
$$ \ int _ {- \ infty} ^ {t} \ delta \ left (t \ right) d \ left (t \ right) = u \ left (t \ right) $$
$$ \ delta \ left (t \ right) = \ frac {du \ left (t \ right)} {d \ left (t \ right)} $$
Сигнал линейного изменения агрегата
Значение единичного линейного сигнала возрастает по экспоненте от источника. Изображение сигнала линейного изменения агрегата показано ниже.
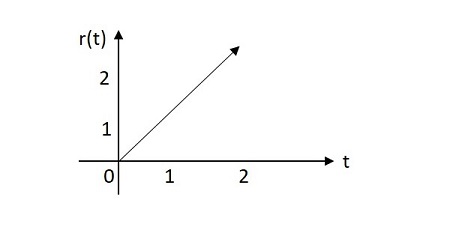
Единичная функция линейного изменения обозначается как u(t). Это определяется как -
$$ \ int_ {0} ^ {t} u \ left (t \ right) d \ left (t \ right) = \ int_ {0} ^ {t} 1 dt = t = r \ left (t \ right) $$
$$ u \ left (t \ right) = \ frac {dr \ left (t \ right)} {dt} $$
Единичный параболический сигнал
Единичный параболический сигнал имеет свое значение, изменяющееся, как парабола в его начале. Изображение единичного параболического сигнала показано ниже.
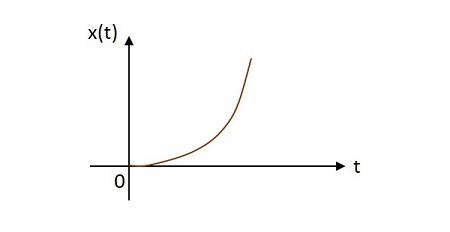
Единичная параболическая функция обозначается $ u \ left (t \ right) $. Это определяется как -
$$ \ int_ {0} ^ {t} \ int_ {0} ^ {t} u \ left (t \ right) dtdt = \ int_ {0} ^ {t} r \ left (t \ right) dt = \ int_ {0} ^ {t} t.dt = \ frac {t ^ {2}} {2} dt = x \ left (t \ right) $$
$$ r \ left (t \ right) = \ frac {dx \ left (t \ right)} {dt} $$
$$ u \ left (t \ right) = \ frac {d ^ {2} x \ left (t \ right)} {dt ^ {2}} $$
Сигнум Функция
Значение функции Signum равномерно распределено как в положительной, так и в отрицательной плоскости от ее источника. Изображение функции Signum показано ниже.
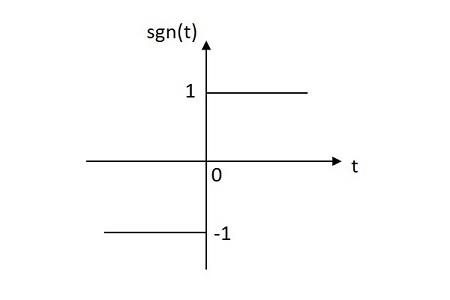
Функция Signum обозначается sgn(t). Он определяется как
$$ sgn \ left (t \ right) = \ left \ {\ begin {matrix} 1 \: \: для \: \: t \ geq 0 \\ - 1 \: \: для \: \: t <0 \ end {matrix} \ right. $$
$$ sign \ left (t \ right) = 2u \ left (t \ right) -1 $$
Экспоненциальный сигнал
Экспоненциальный сигнал имеет значение, экспоненциально изменяющееся от источника. Экспоненциальная функция имеет вид -
$$ x \ left (t \ right) = e ^ {\ alpha t} $$
Форму экспоненты можно определить с помощью $ \ alpha $. Эту функцию можно понять в 3 случаях
Case 1 -
Если $ \ alpha = 0 \ rightarrow x \ left (t \ right) = e ^ {0} = 1 $
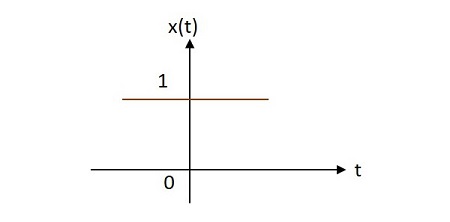
Case 2 -
Если $ \ alpha <0 $, то $ x \ left (t \ right) = e ^ {\ alpha t} $, где $ \ alpha $ отрицательно. Эта форма называетсяdecaying exponential.
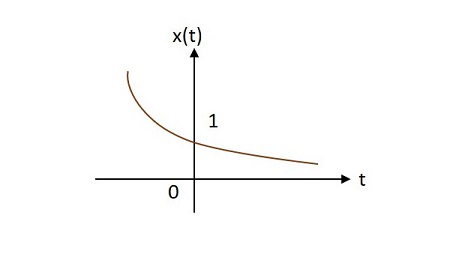
Case 3 -
Если $ \ alpha> 0 $, то $ x \ left (t \ right) = e ^ {\ alpha t} $, где $ \ alpha $ положительно. Эта форма называетсяraising exponential.
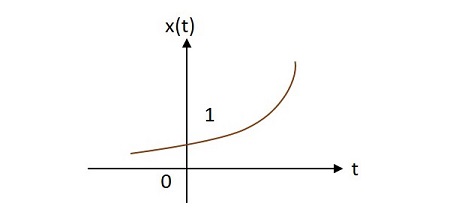
Прямоугольный сигнал
Прямоугольный сигнал имеет свое значение, распределенное в прямоугольной форме как в положительной, так и в отрицательной плоскостях от его источника. Изображение прямоугольного сигнала показано ниже.
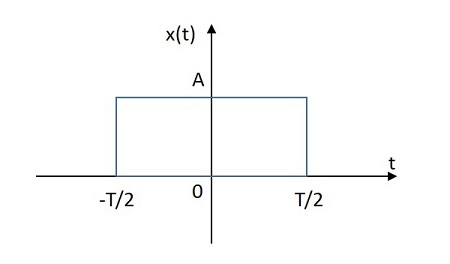
Прямоугольная функция обозначается $ x \ left (t \ right) $. Он определяется как
$$ x \ left (t \ right) = A \: rect \ left [\ frac {t} {T} \ right] $$
Треугольный сигнал
Прямоугольный сигнал имеет свое значение, распределенное в треугольной форме как в положительной, так и в отрицательной плоскостях от его источника. Изображение треугольного сигнала показано ниже.
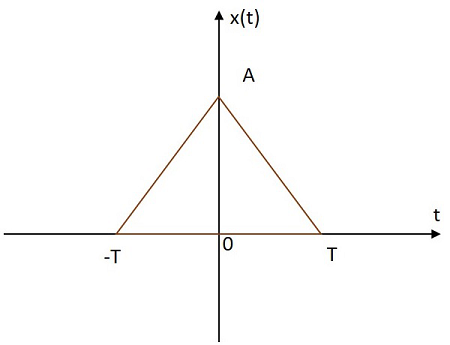
Треугольная функция обозначается $ x \ left (t \ right) $. Он определяется как
$$ x \ left (t \ right) = A \ left [1- \ frac {\ left | t \ right |} {T} \ right] $$
Синусоидальный сигнал
Синусоидальный сигнал имеет значение, синусоидально изменяющееся от его источника. Изображение синусоидального сигнала показано ниже.
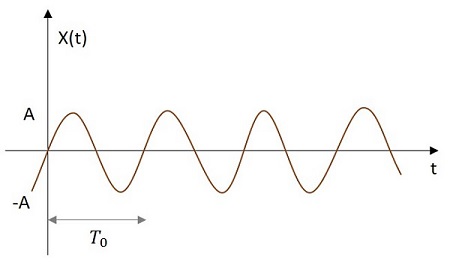
Синусоидальная функция обозначается x (t). Это определяется как -
$$ x \ left (t \ right) = A \ cos \ left (w_ {0} t \ pm \ phi \ right) $$
или же
$$ x \ left (t \ right) = грех \ left (w_ {0} t \ pm \ phi \ right) $$
Где $ T_ {0} = \ frac {2 \ pi} {w_ {0}} $
Функция Sinc
Сигнал Sinc имеет значение, изменяющееся в соответствии с определенным соотношением, как в приведенном ниже уравнении. Он имеет максимальное значение в начале координат и продолжает уменьшаться по мере удаления. Изображение сигнала функции Sinc показано ниже.
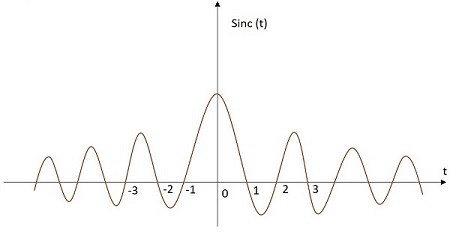
Функция Sinc обозначается через sinc(t). Это определяется как -
$$ sinc \ left (t \ right) = \ frac {sin \ left (\ pi t \ right)} {\ pi t} $$
Итак, это различные сигналы, с которыми мы чаще всего сталкиваемся в области электроники и связи. Каждый сигнал можно определить в математическом уравнении, чтобы упростить анализ сигнала.
Как упоминалось ранее, каждый сигнал имеет определенную форму волны. Формирование волны может изменить содержание сигнала. В любом случае, решение о том, изменять ли волну для какой-либо конкретной схемы, должен принимать инженер-проектировщик. Но для изменения формы волны существует несколько методов, которые будут обсуждаться в следующих разделах.