Машинное обучение с Python - Краткое руководство
Мы живем в «эпоху данных», которая обогащается более высокой вычислительной мощностью и большим объемом ресурсов хранения. Эти данные или информация увеличиваются день ото дня, но настоящая проблема состоит в том, чтобы разобраться во всех данных. Компании и организации пытаются справиться с этим, создавая интеллектуальные системы, используя концепции и методологии Data Science, Data Mining и Machine Learning. Среди них машинное обучение - самая захватывающая область информатики. Было бы неправильно, если бы мы назовем машинное обучение приложением и наукой об алгоритмах, которые придают смысл данным.
Что такое машинное обучение?
Машинное обучение (ML) - это область информатики, с помощью которой компьютерные системы могут обеспечивать понимание данных во многом так же, как это делают люди.
Проще говоря, ML - это тип искусственного интеллекта, который извлекает закономерности из необработанных данных с помощью алгоритма или метода. Основная цель ML - позволить компьютерным системам учиться на собственном опыте без явного программирования или вмешательства человека.
Потребность в машинном обучении
В настоящий момент люди являются наиболее умными и продвинутыми видами на Земле, потому что они могут думать, оценивать и решать сложные проблемы. С другой стороны, ИИ все еще находится на начальной стадии и не превзошел человеческий интеллект во многих аспектах. Тогда возникает вопрос: зачем заставлять машину учиться? Наиболее подходящая причина для этого - «принимать решения на основе данных с эффективностью и масштабом».
В последнее время организации вкладывают значительные средства в новые технологии, такие как искусственный интеллект, машинное обучение и глубокое обучение, чтобы получать ключевую информацию из данных для выполнения нескольких реальных задач и решения проблем. Мы можем назвать это решениями, основанными на данных, которые принимаются машинами, в частности, для автоматизации процесса. Эти решения, основанные на данных, могут использоваться вместо использования логики программирования в задачах, которые не могут быть запрограммированы изначально. Дело в том, что мы не можем обойтись без человеческого интеллекта, но другой аспект заключается в том, что всем нам необходимо решать реальные проблемы с эффективностью в огромных масштабах. Вот почему возникает потребность в машинном обучении.
Почему и когда заставлять машины учиться?
Мы уже обсуждали необходимость машинного обучения, но возникает другой вопрос: в каких сценариях мы должны заставить машину учиться? Может быть несколько обстоятельств, когда нам нужны машины для принятия решений на основе данных с эффективностью и в большом масштабе. Ниже приведены некоторые из таких обстоятельств, при которых заставить машины учиться было бы более эффективно:
Недостаток человеческого опыта
Самый первый сценарий, в котором мы хотим, чтобы машина училась и принимала решения на основе данных, может быть областью, в которой отсутствует человеческий опыт. Примерами могут быть навигации по неизвестным территориям или пространственным планетам.
Динамические сценарии
Есть несколько сценариев, которые по своей природе динамичны, т.е. они постоянно меняются. В случае этих сценариев и поведения мы хотим, чтобы машина училась и принимала решения на основе данных. Некоторыми примерами могут быть подключение к сети и доступность инфраструктуры в организации.
Сложность перевода опыта в вычислительные задачи
Могут быть различные области, в которых люди имеют свой опыт; однако они не могут воплотить этот опыт в вычислительных задачах. В таких обстоятельствах нам нужно машинное обучение. Примерами могут быть области распознавания речи, когнитивные задачи и т. Д.
Модель машинного обучения
Прежде чем обсуждать модель машинного обучения, мы должны понять следующее формальное определение машинного обучения, данное профессором Митчеллом:
«Считается, что компьютерная программа учится на опыте E в отношении некоторого класса задач T и показателя производительности P, если ее производительность при выполнении задач в T, измеренная с помощью P, улучшается с опытом E.»
Приведенное выше определение в основном сосредоточено на трех параметрах, а также на основных компонентах любого алгоритма обучения, а именно на задаче (T), производительности (P) и опыте (E). В этом контексте мы можем упростить это определение как -
ML - это область ИИ, состоящая из алгоритмов обучения, которые:
Улучшите их производительность (P)
При выполнении некоторой задачи (T)
Со временем с опытом (E)
Основываясь на вышеизложенном, следующая диаграмма представляет модель машинного обучения -

Давайте теперь обсудим их подробнее -
Задача (T)
С точки зрения проблемы, мы можем определить задачу T как реальную проблему, которую необходимо решить. Проблема может быть чем угодно, например, найти лучшую цену на дом в определенном месте или найти лучшую маркетинговую стратегию и т. Д. С другой стороны, если мы говорим о машинном обучении, определение задачи другое, потому что трудно решить задачи на основе машинного обучения с помощью традиционный подход к программированию.
Задача T называется задачей на основе машинного обучения, если она основана на процессе, и система должна следовать для работы с точками данных. Примеры задач на основе ML: Классификация, Регрессия, Структурированная аннотация, Кластеризация, Транскрипция и т. Д.
Опыт (E)
Как следует из названия, это знания, полученные из точек данных, предоставленных алгоритму или модели. После предоставления набора данных модель будет запускаться итеративно и изучать некоторый внутренний шаблон. Приобретенное таким образом обучение называется опытом (E). Проводя аналогию с человеческим обучением, мы можем думать об этой ситуации как о том, что человек учится или приобретает некоторый опыт с помощью различных атрибутов, таких как ситуация, отношения и т.д. Опыт, полученный с помощью нашей модели или алгоритма ML, будет использован для решения задачи T.
Производительность (P)
Алгоритм машинного обучения должен выполнять задачу и получать опыт с течением времени. Мера, которая показывает, работает ли алгоритм ML в соответствии с ожиданиями, - это его производительность (P). P - это, по сути, количественный показатель, который показывает, как модель выполняет задачу, T, используя свой опыт, E. Существует множество показателей, которые помогают понять производительность ML, например, оценка точности, оценка F1, матрица путаницы, точность, отзыв , чувствительность и т. д.
Проблемы в обучении машин
Хотя машинное обучение стремительно развивается, добиваясь значительных успехов в области кибербезопасности и автономных автомобилей, этому сегменту ИИ в целом еще предстоит пройти долгий путь. Причина в том, что ML не смог преодолеть ряд проблем. Проблемы, с которыми в настоящее время сталкивается ML:
Quality of data- Наличие качественных данных для алгоритмов машинного обучения - одна из самых больших проблем. Использование некачественных данных приводит к проблемам, связанным с предварительной обработкой данных и извлечением признаков.
Time-Consuming task - Еще одна проблема, с которой сталкиваются модели машинного обучения, - это расход времени, особенно на сбор данных, извлечение функций и поиск.
Lack of specialist persons - Поскольку технология машинного обучения все еще находится на начальной стадии, наличие экспертных ресурсов - сложная задача.
No clear objective for formulating business problems - Отсутствие четкой цели и четко определенной цели для бизнес-проблем - еще одна ключевая проблема для машинного обучения, поскольку эта технология еще не настолько развита.
Issue of overfitting & underfitting - Если модель переоснащается или не подходит, она не может быть хорошо представлена для проблемы.
Curse of dimensionality- Еще одна проблема, с которой сталкивается модель ML, - это слишком много характеристик точек данных. Это может стать настоящей помехой.
Difficulty in deployment - Сложность модели машинного обучения затрудняет развертывание в реальной жизни.
Применение машинного обучения
Машинное обучение - самая быстрорастущая технология, и, по мнению исследователей, мы живем в золотой год AI и ML. Он используется для решения многих реальных сложных проблем, которые не могут быть решены с помощью традиционного подхода. Ниже приведены некоторые реальные приложения ML.
Анализ эмоций
Анализ настроений
Обнаружение и предотвращение ошибок
Прогноз погоды и предсказание
Анализ и прогноз фондового рынка
Синтез речи
Распознавание речи
Сегментация клиентов
Распознавание объекта
Обнаружение мошенничества
Предотвращение мошенничества
Рекомендация товаров покупателю в интернет-магазинах.
Введение в Python
Python - популярный объектно-ориентированный язык программирования, обладающий возможностями языка программирования высокого уровня. Его простой в изучении синтаксис и переносимость делают его популярным в наши дни. Следующие факты дают нам введение в Python -
Python был разработан Гвидо ван Россумом в Stichting Mathematisch Centrum в Нидерландах.
Он был написан как преемник языка программирования под названием «ABC».
Его первая версия была выпущена в 1991 году.
Название Python было выбрано Гвидо ван Россумом из телешоу «Летающий цирк Монти Пайтона».
Это язык программирования с открытым исходным кодом, что означает, что мы можем бесплатно загрузить его и использовать для разработки программ. Его можно скачать с www.python.org .
Язык программирования Python обладает функциями как Java, так и C. Он имеет элегантный код «C» и, с другой стороны, классы и объекты, такие как Java, для объектно-ориентированного программирования.
Это интерпретируемый язык, что означает, что исходный код программы Python сначала будет преобразован в байт-код, а затем выполнен виртуальной машиной Python.
Сильные и слабые стороны Python
У каждого языка программирования есть свои сильные и слабые стороны, как и у Python.
Сильные стороны
Согласно исследованиям и опросам, Python является пятым по важности языком, а также самым популярным языком для машинного обучения и обработки данных. Это из-за следующих сильных сторон Python:
Easy to learn and understand- Синтаксис Python более простой; следовательно, выучить и понять язык относительно легко даже для новичков.
Multi-purpose language - Python - это многоцелевой язык программирования, поскольку он поддерживает структурное программирование, объектно-ориентированное программирование, а также функциональное программирование.
Huge number of modules- Python имеет огромное количество модулей, охватывающих все аспекты программирования. Эти модули легко доступны для использования, что делает Python расширяемым языком.
Support of open source community- Как язык программирования с открытым исходным кодом, Python поддерживается очень большим сообществом разработчиков. Благодаря этому ошибки легко исправляются сообществом Python. Эта характеристика делает Python очень надежным и адаптивным.
Scalability - Python - это масштабируемый язык программирования, поскольку он обеспечивает улучшенную структуру для поддержки больших программ, чем сценарии оболочки.
Слабость
Хотя Python - популярный и мощный язык программирования, у него есть собственная слабость - низкая скорость выполнения.
Скорость выполнения Python медленная по сравнению с компилируемыми языками, потому что Python является интерпретируемым языком. Это может быть основной областью улучшения для сообщества Python.
Установка Python
Для работы в Python мы должны сначала установить его. Вы можете выполнить установку Python любым из следующих двух способов:
Индивидуальная установка Python
Использование предварительно упакованного дистрибутива Python - Anaconda
Давайте обсудим каждый из них подробно.
Индивидуальная установка Python
Если вы хотите установить Python на свой компьютер, то вам необходимо загрузить только двоичный код, применимый для вашей платформы. Дистрибутив Python доступен для платформ Windows, Linux и Mac.
Ниже приводится краткий обзор установки Python на вышеупомянутых платформах.
On Unix and Linux platform
С помощью следующих шагов мы можем установить Python на платформу Unix и Linux -
Сначала перейдите к https://www.python.org/downloads/.
Затем щелкните ссылку, чтобы загрузить заархивированный исходный код, доступный для Unix / Linux.
Теперь загрузите и извлеките файлы.
Затем мы можем отредактировать файл Modules / Setup, если мы хотим настроить некоторые параметры.
Далее напишите команду run ./configure script
make
сделать установку
On Windows platform
С помощью следующих шагов мы можем установить Python на платформу Windows -
Сначала перейдите к https://www.python.org/downloads/.
Затем щелкните ссылку на файл python-XYZ.msi установщика Windows. Здесь XYZ - это версия, которую мы хотим установить.
Теперь мы должны запустить загруженный файл. Это приведет нас к мастеру установки Python, которым легко пользоваться. Теперь примите настройки по умолчанию и дождитесь завершения установки.
On Macintosh platform
Для Mac OS X, Homebrew, для установки Python 3 рекомендуется отличный и простой в использовании установщик пакетов. Если у вас нет Homebrew, вы можете установить его с помощью следующей команды -
$ ruby -e "$(curl -fsSL
https://raw.githubusercontent.com/Homebrew/install/master/install)"Его можно обновить с помощью команды ниже -
$ brew updateТеперь, чтобы установить Python3 в вашу систему, нам нужно выполнить следующую команду -
$ brew install python3Использование предварительно упакованного распространения Python: Anaconda
Anaconda - это пакетная компиляция Python, в которой есть все библиотеки, широко используемые в Data Science. Мы можем выполнить следующие шаги, чтобы настроить среду Python с помощью Anaconda:
Step1- Во-первых, нам нужно скачать необходимый установочный пакет из дистрибутива Anaconda. Ссылка на то же самоеhttps://www.anaconda.com/distribution/. Вы можете выбрать ОС Windows, Mac или Linux в соответствии с вашими требованиями.
Step2- Затем выберите версию Python, которую вы хотите установить на свой компьютер. Последняя версия Python - 3.7. Там вы получите варианты как для 64-битной, так и для 32-битной графической установки.
Step3- После выбора ОС и версии Python он загрузит установщик Anaconda на ваш компьютер. Теперь дважды щелкните файл, и программа установки установит пакет Anaconda.
Step4 - Чтобы проверить, установлен он или нет, откройте командную строку и введите Python следующим образом:

Вы также можете проверить это в подробной видео-лекции на сайтеhttps://www.tutorialspoint.com/python_essentials_online_training/getting_started_with_anaconda.asp.
Почему Python для науки о данных?
Python - пятый по важности язык, а также самый популярный язык для машинного обучения и анализа данных. Ниже перечислены особенности Python, которые делают его предпочтительным языком для науки о данных.
Обширный набор пакетов
Python имеет обширный и мощный набор пакетов, готовых к использованию в различных областях. Он также имеет такие пакеты, как numpy, scipy, pandas, scikit-learn и т. Д., Которые необходимы для машинного обучения и науки о данных.
Легкое прототипирование
Еще одна важная особенность Python, которая делает его предпочтительным языком для науки о данных, - это простое и быстрое прототипирование. Эта функция полезна для разработки нового алгоритма.
Функция совместной работы
Область науки о данных в основном требует хорошего сотрудничества, и Python предоставляет множество полезных инструментов, которые делают это чрезвычайно важным.
Один язык для многих доменов
Типичный проект в области науки о данных включает в себя различные области, такие как извлечение данных, манипулирование данными, анализ данных, извлечение функций, моделирование, оценка, развертывание и обновление решения. Поскольку Python является многоцелевым языком, он позволяет специалистам по обработке данных обращаться ко всем этим доменам с общей платформы.
Компоненты экосистемы Python ML
В этом разделе давайте обсудим некоторые основные библиотеки Data Science, которые составляют компоненты экосистемы машинного обучения Python. Эти полезные компоненты делают Python важным языком для науки о данных. Хотя таких компонентов много, давайте обсудим здесь некоторые из важных компонентов экосистемы Python -
Блокнот Jupyter
Блокноты Jupyter в основном предоставляют интерактивную вычислительную среду для разработки приложений Data Science на базе Python. Ранее они назывались ноутбуками ipython. Ниже приведены некоторые особенности записных книжек Jupyter, которые делают его одним из лучших компонентов экосистемы Python ML.
Блокноты Jupyter могут иллюстрировать процесс анализа шаг за шагом, упорядочивая такие вещи, как код, изображения, текст, вывод и т. Д., Поэтапно.
Это помогает специалисту по обработке данных документировать мыслительный процесс при разработке процесса анализа.
Так же результат можно зафиксировать как часть записной книжки.
С помощью записных книжек jupyter мы также можем поделиться своей работой с коллегами.
Установка и выполнение
Если вы используете дистрибутив Anaconda, вам не нужно устанавливать jupyter notebook отдельно, поскольку он уже установлен вместе с ним. Вам просто нужно перейти в Anaconda Prompt и ввести следующую команду -
C:\>jupyter notebookПосле нажатия Enter будет запущен сервер ноутбука на localhost: 8888 вашего компьютера. Это показано на следующем снимке экрана -

Теперь, после нажатия на вкладку «Новая», вы получите список опций. Выберите Python 3, и вы перейдете в новую записную книжку, чтобы начать в ней работать. Вы увидите это на следующих скриншотах -


С другой стороны, если вы используете стандартный дистрибутив Python, то блокнот jupyter можно установить с помощью популярного установщика пакетов Python, pip.
pip install jupyterТипы ячеек в Jupyter Notebook
Ниже приведены три типа ячеек в записной книжке jupyter:
Code cells- Как следует из названия, мы можем использовать эти ячейки для написания кода. После написания кода / содержимого он отправит его ядру, которое связано с записной книжкой.
Markdown cells- Мы можем использовать эти ячейки для обозначения вычислительного процесса. Они могут содержать такие вещи, как текст, изображения, латексные уравнения, HTML-теги и т. Д.
Raw cells- Написанный в них текст отображается как есть. Эти ячейки в основном используются для добавления текста, который мы не хотим преобразовывать с помощью механизма автоматического преобразования jupyter notebook.
Для более подробного изучения ноутбука jupyter перейдите по ссылкеhttps://www.tutorialspoint.com/jupyter/index.htm.
NumPy
Это еще один полезный компонент, который делает Python одним из любимых языков Data Science. Это в основном означает числовой Python и состоит из объектов многомерного массива. Используя NumPy, мы можем выполнять следующие важные операции:
Математические и логические операции над массивами.
Преобразование Фурье
Операции, связанные с линейной алгеброй.
Мы также можем рассматривать NumPy как замену MatLab, потому что NumPy в основном используется вместе с Scipy (научный Python) и Mat-plotlib (библиотека построения графиков).
Installation and Execution
Если вы используете дистрибутив Anaconda, вам не нужно устанавливать NumPy отдельно, поскольку он уже установлен вместе с ним. Вам просто нужно импортировать пакет в свой скрипт Python, выполнив следующие действия:
import numpy as npС другой стороны, если вы используете стандартный дистрибутив Python, NumPy можно установить с помощью популярного установщика пакетов Python, pip.
pip install NumPyДля более детального изучения NumPy вы можете перейти по ссылкеhttps://www.tutorialspoint.com/numpy/index.htm.
Панды
Это еще одна полезная библиотека Python, которая делает Python одним из любимых языков Data Science. Pandas в основном используется для обработки данных, обработки и анализа. Он был разработан Уэсом МакКинни в 2008 году. С помощью Pandas при обработке данных мы можем выполнить следующие пять шагов:
Load
Prepare
Manipulate
Model
Analyze
Представление данных в пандах
Полное представление данных в Pandas выполняется с помощью следующих трех структур данных:
Series- По сути, это одномерный массив ndarray с меткой оси, что означает, что он похож на простой массив с однородными данными. Например, следующая серия представляет собой набор целых чисел 1,5,10,15,24,25…
| 1 | 5 | 10 | 15 | 24 | 25 | 28 | 36 | 40 | 89 |
Data frame- Это наиболее полезная структура данных, которая используется практически для всех видов представления данных и манипуляций с ними в пандах. По сути, это двухмерная структура данных, которая может содержать разнородные данные. Как правило, табличные данные представлены с помощью фреймов данных. Например, в следующей таблице показаны данные об учениках, у которых есть имена и номера, возраст и пол.
имя |
Номер рулона |
Возраст |
Пол |
|---|---|---|---|
Аарав |
1 |
15 |
мужчина |
Harshit |
2 |
14 |
мужчина |
Каника |
3 |
16 |
женский |
Mayank |
4 |
15 |
мужчина |
Panel- Это трехмерная структура данных, содержащая разнородные данные. Представить панель в графическом виде очень сложно, но ее можно проиллюстрировать как контейнер DataFrame.
В следующей таблице приведены размеры и описание вышеупомянутых структур данных, используемых в Pandas.
Структура данных |
Размер |
Описание |
|---|---|---|
Серии |
1-D |
Неизменяемый размер, однородные одномерные данные |
DataFrames |
2-D |
Изменяемый размер, гетерогенные данные в табличной форме |
Панель |
3-D |
Массив изменяемого размера, контейнер DataFrame. |
Мы можем понять эти структуры данных, поскольку структура данных более высокого измерения является контейнером структуры данных более низкого измерения.
Установка и выполнение
Если вы используете дистрибутив Anaconda, вам не нужно устанавливать Pandas отдельно, поскольку он уже установлен вместе с ним. Вам просто нужно импортировать пакет в свой скрипт Python, выполнив следующие действия:
import pandas as pdС другой стороны, если вы используете стандартный дистрибутив Python, Pandas можно установить с помощью популярного установщика пакетов python, pip.
pip install PandasПосле установки Pandas вы можете импортировать его в свой скрипт Python, как описано выше.
пример
Ниже приведен пример создания серии из ndarray с использованием Pandas -
In [1]: import pandas as pd
In [2]: import numpy as np
In [3]: data = np.array(['g','a','u','r','a','v'])
In [4]: s = pd.Series(data)
In [5]: print (s)
0 g
1 a
2 u
3 r
4 a
5 v
dtype: objectДля более детального изучения Pandas вы можете перейти по ссылке https://www.tutorialspoint.com/python_pandas/index.htm.
Scikit-Learn
Еще одна полезная и самая важная библиотека Python для науки о данных и машинного обучения на Python - это Scikit-learn. Ниже приведены некоторые особенности Scikit-learn, которые делают его таким полезным:
Он построен на NumPy, SciPy и Matplotlib.
Это открытый исходный код, и его можно повторно использовать по лицензии BSD.
Он доступен каждому и может использоваться повторно в различных контекстах.
С его помощью можно реализовать широкий спектр алгоритмов машинного обучения, охватывающих основные области машинного обучения, такие как классификация, кластеризация, регрессия, уменьшение размерности, выбор модели и т. Д.
Установка и выполнение
Если вы используете дистрибутив Anaconda, вам не нужно устанавливать Scikit-learn отдельно, поскольку он уже установлен вместе с ним. Вам просто нужно использовать этот пакет в своем скрипте Python. Например, с помощью следующей строки скрипта мы импортируем набор данных о пациентах с раком груди изScikit-learn -
from sklearn.datasets import load_breast_cancerС другой стороны, если вы используете стандартный дистрибутив Python и у вас есть NumPy и SciPy, то Scikit-learn можно установить с помощью популярного установщика пакетов Python, pip.
pip install -U scikit-learnПосле установки Scikit-learn вы можете использовать его в своем скрипте Python, как вы это делали выше.
Существуют различные алгоритмы, техники и методы машинного обучения, которые можно использовать для построения моделей для решения реальных проблем с использованием данных. В этой главе мы собираемся обсудить такие разные виды методов.
Различные типы методов
Ниже приведены различные методы машинного обучения, основанные на некоторых широких категориях:
На основе наблюдения человека
В процессе обучения некоторые методы, основанные на контроле человека, следующие:
Supervised Learning
Алгоритмы или методы контролируемого обучения являются наиболее часто используемыми алгоритмами машинного обучения. Этот метод или алгоритм обучения берет образец данных, то есть обучающие данные, и связанный с ним вывод, то есть метки или ответы с каждой выборкой данных во время процесса обучения.
Основная цель алгоритмов контролируемого обучения - изучить связь между выборками входных данных и соответствующими выходными данными после выполнения нескольких экземпляров обучающих данных.
Например, у нас есть
x: входные переменные и
Y: выходная переменная
Теперь примените алгоритм для изучения функции сопоставления от входа к выходу следующим образом:
Y = f (x)
Теперь основная цель - так аппроксимировать функцию отображения, чтобы даже при наличии новых входных данных (x) мы могли легко предсказать выходную переменную (Y) для этих новых входных данных.
Это называется контролируемым, потому что весь процесс обучения можно представить себе так, как будто он находится под наблюдением учителя или супервизора. Примеры контролируемых алгоритмов машинного обучения:Decision tree, Random Forest, KNN, Logistic Regression и т.п.
Основываясь на задачах машинного обучения, алгоритмы контролируемого обучения можно разделить на следующие два широких класса:
Classification
Regression
Classification
Ключевой целью задач на основе классификации является прогнозирование категориальных выходных меток или ответов для заданных входных данных. Результат будет основан на том, что модель узнала на этапе обучения. Как мы знаем, категориальные выходные ответы означают неупорядоченные и дискретные значения, следовательно, каждый выходной ответ будет принадлежать определенному классу или категории. Мы также подробно обсудим классификацию и связанные с ней алгоритмы в следующих главах.
Regression
Ключевой целью задач на основе регрессии является прогнозирование выходных меток или ответов, которые являются продолжением числовых значений для заданных входных данных. Результат будет основан на том, что модель узнала на этапе обучения. По сути, регрессионные модели используют функции входных данных (независимые переменные) и соответствующие им непрерывные числовые выходные значения (зависимые или выходные переменные) для изучения конкретной связи между входами и соответствующими выходными данными. Мы также подробно обсудим регрессию и связанные с ней алгоритмы в следующих главах.
Неконтролируемое обучение
Как следует из названия, он противоположен контролируемым методам или алгоритмам машинного обучения, что означает, что в алгоритмах неконтролируемого машинного обучения у нас нет руководителя, который мог бы предоставить какие-либо рекомендации. Алгоритмы неконтролируемого обучения удобны в сценарии, в котором у нас нет свободы, как в алгоритмах контролируемого обучения, иметь предварительно помеченные данные обучения, и мы хотим извлечь полезный шаблон из входных данных.
Например, это можно понять так -
Предположим, у нас есть -
x: Input variables, тогда не будет соответствующей выходной переменной, и алгоритмам потребуется обнаруживать интересную закономерность в данных для обучения.
Примеры алгоритмов машинного обучения без учителя включают кластеризацию K-средних, K-nearest neighbors и т.п.
Основываясь на задачах машинного обучения, алгоритмы неконтролируемого обучения можно разделить на следующие широкие классы:
Clustering
Association
Снижение размерности
Clustering
Методы кластеризации - один из самых полезных методов машинного обучения без учителя. Эти алгоритмы используются для поиска сходства, а также шаблонов отношений между выборками данных, а затем группируют эти выборки в группы, имеющие сходство на основе характеристик. Реальный пример кластеризации - это группировка клиентов по их покупательскому поведению.
Association
Еще один полезный метод машинного обучения без учителя - это Associationкоторый используется для анализа большого набора данных, чтобы найти закономерности, которые дополнительно представляют интересные отношения между различными элементами. Его также называютAssociation Rule Mining или же Market basket analysis который в основном используется для анализа моделей покупок клиентов.
Dimensionality Reduction
Этот метод машинного обучения без учителя используется для уменьшения количества переменных характеристик для каждой выборки данных путем выбора набора основных или репрезентативных функций. Здесь возникает вопрос, а зачем нам уменьшать размерность? Причина кроется в проблеме сложности пространства функций, которая возникает, когда мы начинаем анализировать и извлекать миллионы функций из выборок данных. Эта проблема обычно относится к «проклятию размерности». PCA (анализ главных компонентов), K-ближайших соседей и дискриминантный анализ - некоторые из популярных алгоритмов для этой цели.
Anomaly Detection
Этот метод машинного обучения без учителя используется для обнаружения редких событий или наблюдений, которые обычно не происходят. Используя полученные знания, методы обнаружения аномалий смогут различать аномальные и нормальные точки данных. Некоторые из неконтролируемых алгоритмов, таких как кластеризация, KNN могут обнаруживать аномалии на основе данных и их функций.
Полу-контролируемое обучение
Такие алгоритмы или методы не являются ни полностью контролируемыми, ни полностью неконтролируемыми. По сути, они находятся между двумя методами обучения - контролируемым и неконтролируемым обучением. Эти виды алгоритмов обычно используют небольшой контролируемый обучающий компонент, т.е. небольшой объем предварительно помеченных аннотированных данных и большой неконтролируемый обучающий компонент, то есть множество немаркированных данных для обучения. Мы можем использовать любой из следующих подходов для реализации методов полууправляемого обучения:
Первый и простой подход - построить контролируемую модель на основе небольшого количества помеченных и аннотированных данных, а затем построить неконтролируемую модель, применив ее к большим объемам немаркированных данных, чтобы получить больше помеченных выборок. Теперь натренируйте на них модель и повторите процесс.
- , p> Второй подход требует дополнительных усилий. В этом подходе мы можем сначала использовать неконтролируемые методы для кластеризации похожих выборок данных, аннотировать эти группы, а затем использовать комбинацию этой информации для обучения модели.
Обучение с подкреплением
Эти методы отличаются от ранее изученных и также используются очень редко. В алгоритмах такого типа обучения будет агент, которого мы хотим обучать в течение определенного периода времени, чтобы он мог взаимодействовать с определенной средой. Агент будет следовать набору стратегий для взаимодействия с окружающей средой, а затем после наблюдения за окружающей средой он будет предпринимать действия в отношении текущего состояния среды. Ниже приведены основные этапы методов обучения с подкреплением.
Step1 - Во-первых, нам нужно подготовить агента с некоторым начальным набором стратегий.
Step2 - Затем понаблюдайте за окружающей средой и ее текущим состоянием.
Step3 - Затем выберите оптимальную политику в отношении текущего состояния среды и выполните важные действия.
Step4 - Теперь агент может получить соответствующее вознаграждение или штраф в соответствии с действием, предпринятым им на предыдущем шаге.
Step5 - Теперь мы можем обновлять стратегии, если это необходимо.
Step6 - Наконец, повторите шаги 2–5, пока агент не научится и не примет оптимальную политику.
Задачи, подходящие для машинного обучения
На следующей диаграмме показано, какой тип задачи подходит для различных проблем машинного обучения.

На основе способности к обучению
В процессе обучения следующие методы основаны на способности к обучению:
Batch Learning
Во многих случаях у нас есть сквозные системы машинного обучения, в которых нам нужно обучить модель за один раз, используя все доступные данные обучения. Такой метод обучения или алгоритм называетсяBatch or Offline learning. Это называется пакетным или автономным обучением, потому что это однократная процедура, и модель будет обучаться с данными одним пакетом. Ниже приведены основные этапы методов пакетного обучения.
Step1 - Во-первых, нам нужно собрать все данные для обучения, чтобы начать обучение модели.
Step2 - Теперь начните обучение модели, предоставив все данные обучения за один раз.
Step3 - Затем прекратите обучение / тренировочный процесс, как только вы получите удовлетворительные результаты / производительность.
Step4- Наконец, разверните эту обученную модель в производстве. Здесь он предсказывает вывод для новой выборки данных.
Онлайн обучение
Это полностью противоположно пакетным или автономным методам обучения. В этих методах обучения обучающие данные поступают в алгоритм несколькими инкрементными пакетами, называемыми мини-пакетами. Ниже приведены основные этапы методов онлайн-обучения.
Step1 - Во-первых, нам нужно собрать все обучающие данные для начала обучения модели.
Step2 - Теперь начните обучение модели, предоставив алгоритму мини-пакет обучающих данных.
Step3 - Затем нам нужно предоставить алгоритму мини-пакеты обучающих данных с несколькими приращениями.
Step4 - Поскольку он не остановится, как пакетное обучение, поэтому после предоставления всех обучающих данных в мини-пакетах предоставьте ему также новые образцы данных.
Step5 - Наконец, он будет продолжать обучение в течение определенного периода времени на основе новых выборок данных.
На основе обобщающего подхода
В процессе обучения следующие методы основаны на обобщающих подходах:
Обучение на основе экземпляров
Метод обучения на основе экземпляров - один из полезных методов построения моделей машинного обучения путем обобщения на основе входных данных. Это противоположно ранее изученным методам обучения в том, что этот вид обучения включает системы машинного обучения, а также методы, которые используют сами точки исходных данных для получения результатов для более новых образцов данных без построения явной модели на данных обучения.
Проще говоря, обучение на основе экземпляров в основном начинается с просмотра точек входных данных, а затем, используя метрику сходства, оно обобщает и предсказывает новые точки данных.
Обучение на основе модели
В методах обучения на основе моделей итеративный процесс выполняется на моделях машинного обучения, которые построены на основе различных параметров модели, называемых гиперпараметрами, и в которых входные данные используются для извлечения функций. В этом обучении гиперпараметры оптимизируются на основе различных методов проверки модели. Вот почему мы можем сказать, что методы обучения на основе моделей используют более традиционный подход машинного обучения к обобщению.
Предположим, что если вы хотите начать проект машинного обучения, то что в первую очередь и самое важное вам потребуется? Это данные, которые нам нужно загрузить для запуска любого проекта ML. Что касается данных, наиболее распространенным форматом данных для проектов машинного обучения является CSV (значения, разделенные запятыми).
По сути, CSV - это простой формат файла, который используется для хранения табличных данных (числа и текста), таких как электронная таблица, в виде обычного текста. В Python мы можем загружать данные CSV различными способами, но перед загрузкой данных CSV мы должны позаботиться о некоторых соображениях.
Учет при загрузке данных CSV
Формат данных CSV является наиболее распространенным форматом для данных ML, но мы должны позаботиться о следующих основных соображениях при загрузке его в наши проекты ML:
Заголовок файла
В файлах данных CSV заголовок содержит информацию для каждого поля. Мы должны использовать один и тот же разделитель для файла заголовка и для файла данных, потому что именно файл заголовка определяет, как следует интерпретировать поля данных.
Ниже приведены два случая, связанных с заголовком файла CSV, которые необходимо учитывать:
Case-I: When Data file is having a file header - Он автоматически назначит имена каждому столбцу данных, если файл данных имеет заголовок.
Case-II: When Data file is not having a file header - Нам нужно присвоить имена каждому столбцу данных вручную, если файл данных не имеет заголовка.
В обоих случаях нам необходимо явно указать, будет ли наш CSV-файл содержать заголовок или нет.
Комментарии
Комментарии в любом файле данных имеют значение. В файле данных CSV комментарии обозначаются решеткой (#) в начале строки. Нам необходимо учитывать комментарии при загрузке данных CSV в проекты ML, потому что, если у нас есть комментарии в файле, нам может потребоваться указать, в зависимости от метода, который мы выбираем для загрузки, следует ли ожидать этих комментариев или нет.
Разделитель
В файлах данных CSV стандартным разделителем является запятая (,). Роль разделителя заключается в разделении значений в полях. Важно учитывать роль разделителя при загрузке файла CSV в проекты ML, потому что мы также можем использовать другой разделитель, такой как табуляция или пробел. Но в случае использования разделителя, отличного от стандартного, мы должны указать его явно.
Цитаты
В файлах данных CSV двойные кавычки («») являются символом кавычек по умолчанию. Важно учитывать роль кавычек при загрузке файла CSV в проекты ML, потому что мы также можем использовать другие символы кавычек, кроме двойных кавычек. Но в случае использования символа кавычки, отличного от стандартного, мы должны указать его явно.
Способы загрузки файла данных CSV
При работе с проектами машинного обучения важнейшая задача - правильно загрузить в него данные. Наиболее распространенным форматом данных для проектов машинного обучения является CSV, он бывает разных видов и имеет разные сложности для анализа. В этом разделе мы собираемся обсудить три распространенных подхода в Python для загрузки файла данных CSV:
Загрузить CSV с помощью стандартной библиотеки Python
Первый и наиболее часто используемый подход для загрузки файла данных CSV - это использование стандартной библиотеки Python, которая предоставляет нам множество встроенных модулей, а именно модуль csv и функцию reader (). Ниже приведен пример загрузки файла данных CSV с его помощью:
пример
В этом примере мы используем набор данных цветка ириса, который можно загрузить в наш локальный каталог. После загрузки файла данных мы можем преобразовать его в массив NumPy и использовать для проектов ML. Ниже приведен сценарий Python для загрузки файла данных CSV.
Во-первых, нам нужно импортировать модуль csv, предоставляемый стандартной библиотекой Python, следующим образом:
import csvДалее нам нужно импортировать модуль Numpy для преобразования загруженных данных в массив NumPy.
import numpy as npТеперь укажите полный путь к файлу, хранящемуся в нашем локальном каталоге, с файлом данных CSV -
path = r"c:\iris.csv"Затем используйте функцию csv.reader () для чтения данных из файла CSV -
with open(path,'r') as f:
reader = csv.reader(f,delimiter = ',')
headers = next(reader)
data = list(reader)
data = np.array(data).astype(float)Мы можем распечатать имена заголовков с помощью следующей строки скрипта -
print(headers)Следующая строка скрипта напечатает форму данных, то есть количество строк и столбцов в файле -
print(data.shape)Следующая строка скрипта даст первые три строки файла данных -
print(data[:3])Output
['sepal_length', 'sepal_width', 'petal_length', 'petal_width']
(150, 4)
[ [5.1 3.5 1.4 0.2]
[4.9 3. 1.4 0.2]
[4.7 3.2 1.3 0.2]]Загрузить CSV с помощью NumPy
Другой подход к загрузке файла данных CSV - это функция NumPy и numpy.loadtxt (). Ниже приведен пример загрузки файла данных CSV с его помощью:
пример
В этом примере мы используем набор данных индейцев пима, содержащий данные о пациентах с диабетом. Этот набор данных представляет собой числовой набор данных без заголовка. Его также можно загрузить в наш локальный каталог. После загрузки файла данных мы можем преобразовать его в массив NumPy и использовать для проектов ML. Ниже приведен сценарий Python для загрузки файла данных CSV.
from numpy import loadtxt
path = r"C:\pima-indians-diabetes.csv"
datapath= open(path, 'r')
data = loadtxt(datapath, delimiter=",")
print(data.shape)
print(data[:3])Вывод
(768, 9)
[ [ 6. 148. 72. 35. 0. 33.6 0.627 50. 1.]
[ 1. 85. 66. 29. 0. 26.6 0.351 31. 0.]
[ 8. 183. 64. 0. 0. 23.3 0.672 32. 1.]]Загрузить CSV с помощью Pandas
Другой подход к загрузке файла данных CSV - использование функции Pandas и pandas.read_csv (). Это очень гибкая функция, которая возвращает pandas.DataFrame, который можно сразу использовать для построения графика. Ниже приведен пример загрузки файла данных CSV с его помощью:
пример
Здесь мы будем реализовывать два сценария Python, первый - с набором данных Iris с заголовками, а другой - с использованием набора данных индейцев пима, который представляет собой числовой набор данных без заголовка. Оба набора данных можно загрузить в локальный каталог.
Script-1
Ниже приведен сценарий Python для загрузки файла данных CSV с использованием Pandas в наборе данных Iris.
from pandas import read_csv
path = r"C:\iris.csv"
data = read_csv(path)
print(data.shape)
print(data[:3])
Output:
(150, 4)
sepal_length sepal_width petal_length petal_width
0 5.1 3.5 1.4 0.2
1 4.9 3.0 1.4 0.2
2 4.7 3.2 1.3 0.2Script-2
Ниже приведен скрипт Python для загрузки файла данных CSV, а также предоставления имен заголовков с использованием Pandas в наборе данных Pima Indians Diabetes.
from pandas import read_csv
path = r"C:\pima-indians-diabetes.csv"
headernames = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=headernames)
print(data.shape)
print(data[:3])Output
(768, 9)
preg plas pres skin test mass pedi age class
0 6 148 72 35 0 33.6 0.627 50 1
1 1 85 66 29 0 26.6 0.351 31 0
2 8 183 64 0 0 23.3 0.672 32 1Разницу между тремя использованными выше подходами к загрузке файла данных CSV можно легко понять с помощью приведенных примеров.
Введение
При работе с проектами машинного обучения мы обычно игнорируем две наиболее важные части, которые называются mathematics и data. Это потому, что мы знаем, что машинное обучение - это подход, основанный на данных, и наша модель машинного обучения будет давать только такие хорошие или плохие результаты, как и данные, которые мы ей предоставили.
В предыдущей главе мы обсуждали, как мы можем загрузить данные CSV в наш проект машинного обучения, но было бы хорошо понять данные перед их загрузкой. Мы можем понимать данные двумя способами: с помощью статистики и с помощью визуализации.
В этой главе с помощью следующих рецептов Python мы собираемся понять данные машинного обучения со статистикой.
Просмотр необработанных данных
Самый первый рецепт - посмотреть на ваши необработанные данные. Важно смотреть на необработанные данные, потому что понимание, которое мы получим после просмотра необработанных данных, повысит наши шансы на лучшую предварительную обработку, а также обработку данных для проектов машинного обучения.
Ниже приведен сценарий Python, реализованный с использованием функции head () фрейма данных Pandas в наборе данных о диабете индейцев пима, чтобы просмотреть первые 50 строк, чтобы лучше понять это.
пример
from pandas import read_csv
path = r"C:\pima-indians-diabetes.csv"
headernames = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=headernames)
print(data.head(50))Вывод
preg plas pres skin test mass pedi age class
0 6 148 72 35 0 33.6 0.627 50 1
1 1 85 66 29 0 26.6 0.351 31 0
2 8 183 64 0 0 23.3 0.672 32 1
3 1 89 66 23 94 28.1 0.167 21 0
4 0 137 40 35 168 43.1 2.288 33 1
5 5 116 74 0 0 25.6 0.201 30 0
6 3 78 50 32 88 31.0 0.248 26 1
7 10 115 0 0 0 35.3 0.134 29 0
8 2 197 70 45 543 30.5 0.158 53 1
9 8 125 96 0 0 0.0 0.232 54 1
10 4 110 92 0 0 37.6 0.191 30 0
11 10 168 74 0 0 38.0 0.537 34 1
12 10 139 80 0 0 27.1 1.441 57 0
13 1 189 60 23 846 30.1 0.398 59 1
14 5 166 72 19 175 25.8 0.587 51 1
15 7 100 0 0 0 30.0 0.484 32 1
16 0 118 84 47 230 45.8 0.551 31 1
17 7 107 74 0 0 29.6 0.254 31 1
18 1 103 30 38 83 43.3 0.183 33 0
19 1 115 70 30 96 34.6 0.529 32 1
20 3 126 88 41 235 39.3 0.704 27 0
21 8 99 84 0 0 35.4 0.388 50 0
22 7 196 90 0 0 39.8 0.451 41 1
23 9 119 80 35 0 29.0 0.263 29 1
24 11 143 94 33 146 36.6 0.254 51 1
25 10 125 70 26 115 31.1 0.205 41 1
26 7 147 76 0 0 39.4 0.257 43 1
27 1 97 66 15 140 23.2 0.487 22 0
28 13 145 82 19 110 22.2 0.245 57 0
29 5 117 92 0 0 34.1 0.337 38 0
30 5 109 75 26 0 36.0 0.546 60 0
31 3 158 76 36 245 31.6 0.851 28 1
32 3 88 58 11 54 24.8 0.267 22 0
33 6 92 92 0 0 19.9 0.188 28 0
34 10 122 78 31 0 27.6 0.512 45 0
35 4 103 60 33 192 24.0 0.966 33 0
36 11 138 76 0 0 33.2 0.420 35 0
37 9 102 76 37 0 32.9 0.665 46 1
38 2 90 68 42 0 38.2 0.503 27 1
39 4 111 72 47 207 37.1 1.390 56 1
40 3 180 64 25 70 34.0 0.271 26 0
41 7 133 84 0 0 40.2 0.696 37 0
42 7 106 92 18 0 22.7 0.235 48 0
43 9 171 110 24 240 45.4 0.721 54 1
44 7 159 64 0 0 27.4 0.294 40 0
45 0 180 66 39 0 42.0 1.893 25 1
46 1 146 56 0 0 29.7 0.564 29 0
47 2 71 70 27 0 28.0 0.586 22 0
48 7 103 66 32 0 39.1 0.344 31 1
49 7 105 0 0 0 0.0 0.305 24 0Из приведенного выше вывода видно, что в первом столбце указан номер строки, который может быть очень полезен для ссылки на конкретное наблюдение.
Проверка размеров данных
Всегда полезно знать, сколько данных в виде строк и столбцов у нас есть для нашего проекта ML. Причины -
Предположим, что если у нас слишком много строк и столбцов, то на запуск алгоритма и обучение модели потребуется много времени.
Предположим, что если у нас будет слишком мало строк и столбцов, у нас не будет достаточно данных для хорошего обучения модели.
Ниже приведен сценарий Python, реализованный путем печати свойства формы во фрейме данных Pandas. Мы собираемся реализовать его на наборе данных iris, чтобы получить в нем общее количество строк и столбцов.
пример
from pandas import read_csv
path = r"C:\iris.csv"
data = read_csv(path)
print(data.shape)Вывод
(150, 4)Из выходных данных легко заметить, что набор данных iris, который мы собираемся использовать, имеет 150 строк и 4 столбца.
Получение типа данных каждого атрибута
Еще одна хорошая практика - знать тип данных каждого атрибута. Причина в том, что в соответствии с требованиями иногда нам может потребоваться преобразовать один тип данных в другой. Например, нам может потребоваться преобразовать строку в числа с плавающей запятой или int для представления категориальных или порядковых значений. Мы можем иметь представление о типе данных атрибута, глядя на необработанные данные, но другой способ - использовать свойство dtypes Pandas DataFrame. С помощью свойства dtypes мы можем категоризировать каждый тип данных атрибутов. Это можно понять с помощью следующего скрипта Python -
пример
from pandas import read_csv
path = r"C:\iris.csv"
data = read_csv(path)
print(data.dtypes)Вывод
sepal_length float64
sepal_width float64
petal_length float64
petal_width float64
dtype: objectИз вышеприведенного вывода мы можем легко получить типы данных каждого атрибута.
Статистическая сводка данных
Мы обсудили рецепт Python для получения формы, то есть количества строк и столбцов данных, но много раз нам нужно просматривать сводки на основе этой формы данных. Это можно сделать с помощью функции describe () в Pandas DataFrame, которая дополнительно предоставляет следующие 8 статистических свойств каждого и каждого атрибута данных:
Count
Mean
Среднеквадратичное отклонение
Минимальное значение
Максимальное значение
25%
Медиана, т.е. 50%
75%
пример
from pandas import read_csv
from pandas import set_option
path = r"C:\pima-indians-diabetes.csv"
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=names)
set_option('display.width', 100)
set_option('precision', 2)
print(data.shape)
print(data.describe())Вывод
(768, 9)
preg plas pres skin test mass pedi age class
count 768.00 768.00 768.00 768.00 768.00 768.00 768.00 768.00 768.00
mean 3.85 120.89 69.11 20.54 79.80 31.99 0.47 33.24 0.35
std 3.37 31.97 19.36 15.95 115.24 7.88 0.33 11.76 0.48
min 0.00 0.00 0.00 0.00 0.00 0.00 0.08 21.00 0.00
25% 1.00 99.00 62.00 0.00 0.00 27.30 0.24 24.00 0.00
50% 3.00 117.00 72.00 23.00 30.50 32.00 0.37 29.00 0.00
75% 6.00 140.25 80.00 32.00 127.25 36.60 0.63 41.00 1.00
max 17.00 199.00 122.00 99.00 846.00 67.10 2.42 81.00 1.00Из вышеприведенного вывода мы можем наблюдать статистическую сводку данных набора данных Pima Indian Diabetes вместе с формой данных.
Анализ распределения классов
Статистика распределения классов полезна в задачах классификации, где нам нужно знать баланс значений классов. Важно знать распределение значений классов, потому что, если у нас очень несбалансированное распределение классов, то есть один класс имеет намного больше наблюдений, чем другой класс, тогда ему может потребоваться особая обработка на этапе подготовки данных нашего проекта ML. Мы можем легко получить распределение классов в Python с помощью Pandas DataFrame.
пример
from pandas import read_csv
path = r"C:\pima-indians-diabetes.csv"
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=names)
count_class = data.groupby('class').size()
print(count_class)Вывод
Class
0 500
1 268
dtype: int64Из приведенного выше вывода ясно видно, что количество наблюдений с классом 0 почти вдвое превышает количество наблюдений с классом 1.
Обзор корреляции между атрибутами
Связь между двумя переменными называется корреляцией. В статистике наиболее распространенным методом вычисления корреляции является коэффициент корреляции Пирсона. Он может иметь три следующих значения:
Coefficient value = 1 - представляет собой полную positive корреляция между переменными.
Coefficient value = -1 - представляет собой полную negative корреляция между переменными.
Coefficient value = 0 - Он представляет no корреляция вообще между переменными.
Для нас всегда полезно просматривать попарные корреляции атрибутов в нашем наборе данных, прежде чем использовать его в проекте машинного обучения, потому что некоторые алгоритмы машинного обучения, такие как линейная регрессия и логистическая регрессия, будут плохо работать, если у нас есть сильно коррелированные атрибуты. В Python мы можем легко вычислить корреляционную матрицу атрибутов набора данных с помощью функции corr () в Pandas DataFrame.
пример
from pandas import read_csv
from pandas import set_option
path = r"C:\pima-indians-diabetes.csv"
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=names)
set_option('display.width', 100)
set_option('precision', 2)
correlations = data.corr(method='pearson')
print(correlations)Вывод
preg plas pres skin test mass pedi age class
preg 1.00 0.13 0.14 -0.08 -0.07 0.02 -0.03 0.54 0.22
plas 0.13 1.00 0.15 0.06 0.33 0.22 0.14 0.26 0.47
pres 0.14 0.15 1.00 0.21 0.09 0.28 0.04 0.24 0.07
skin -0.08 0.06 0.21 1.00 0.44 0.39 0.18 -0.11 0.07
test -0.07 0.33 0.09 0.44 1.00 0.20 0.19 -0.04 0.13
mass 0.02 0.22 0.28 0.39 0.20 1.00 0.14 0.04 0.29
pedi -0.03 0.14 0.04 0.18 0.19 0.14 1.00 0.03 0.17
age 0.54 0.26 0.24 -0.11 -0.04 0.04 0.03 1.00 0.24
class 0.22 0.47 0.07 0.07 0.13 0.29 0.17 0.24 1.00Матрица в приведенных выше выходных данных дает корреляцию между всеми парами атрибутов в наборе данных.
Анализ перекоса распределения атрибутов
Асимметрия может быть определена как распределение, которое предполагается гауссовым, но выглядит искаженным или смещенным в том или ином направлении, либо влево, либо вправо. Проверка асимметрии атрибутов является одной из важных задач по следующим причинам:
Наличие асимметрии данных требует корректировки на этапе подготовки данных, чтобы мы могли получить большую точность от нашей модели.
Большинство алгоритмов машинного обучения предполагает, что данные имеют гауссовское распределение, то есть нормальное или криволинейное.
В Python мы можем легко вычислить перекос каждого атрибута, используя функцию skew () в Pandas DataFrame.
пример
from pandas import read_csv
path = r"C:\pima-indians-diabetes.csv"
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=names)
print(data.skew())Вывод
preg 0.90
plas 0.17
pres -1.84
skin 0.11
test 2.27
mass -0.43
pedi 1.92
age 1.13
class 0.64
dtype: float64Из вышеприведенного вывода можно наблюдать положительный или отрицательный перекос. Если значение ближе к нулю, то перекос меньше.
Введение
В предыдущей главе мы обсудили важность данных для алгоритмов машинного обучения, а также некоторые рецепты Python для понимания данных со статистикой. Есть еще один способ, называемый визуализацией, для понимания данных.
С помощью визуализации данных мы можем увидеть, как данные выглядят и какая корреляция поддерживается атрибутами данных. Это самый быстрый способ узнать, соответствуют ли функции выходным данным. С помощью следующих рецептов Python мы можем понять данные машинного обучения со статистикой.

Одномерные графики: независимое понимание атрибутов
Самый простой тип визуализации - визуализация с одной переменной или «одномерная» визуализация. С помощью одномерной визуализации мы можем понять каждый атрибут нашего набора данных независимо. Ниже приведены некоторые методы в Python для реализации одномерной визуализации.
Гистограммы
Гистограммы группируют данные по ячейкам и являются самым быстрым способом получить представление о распределении каждого атрибута в наборе данных. Ниже приведены некоторые характеристики гистограмм -
Он предоставляет нам подсчет количества наблюдений в каждой ячейке, созданной для визуализации.
По форме бункера мы можем легко наблюдать распределение, т. Е. Является ли оно гауссовым, асимметричным или экспоненциальным.
Гистограммы также помогают нам увидеть возможные выбросы.
пример
Код, показанный ниже, является примером сценария Python, создающего гистограмму атрибутов набора данных Pima Indian Diabetes. Здесь мы будем использовать функцию hist () в Pandas DataFrame для создания гистограмм иmatplotlib для их построения.
from matplotlib import pyplot
from pandas import read_csv
path = r"C:\pima-indians-diabetes.csv"
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=names)
data.hist()
pyplot.show()Вывод
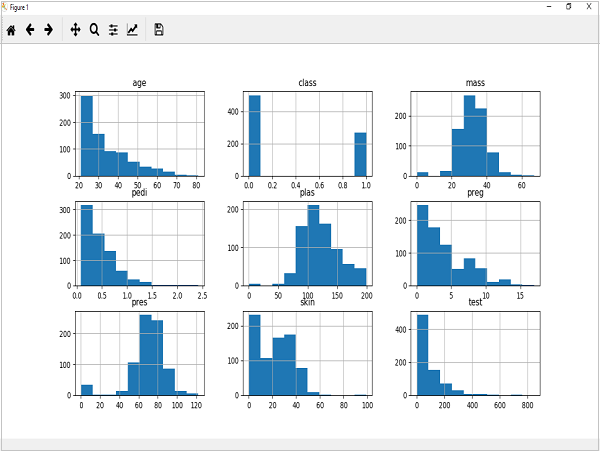
Приведенный выше вывод показывает, что он создал гистограмму для каждого атрибута в наборе данных. Исходя из этого, мы можем наблюдать, что, возможно, возраст, педиатрия и атрибуты теста могут иметь экспоненциальное распределение, тогда как масса и плазма имеют гауссово распределение.
Графики плотности
Еще один быстрый и простой метод получения распределения каждого атрибута - это графики плотности. Это также похоже на гистограмму, но с плавной кривой, проведенной через верх каждой ячейки. Мы можем назвать их абстрактными гистограммами.
пример
В следующем примере скрипт Python сгенерирует графики плотности для распределения атрибутов набора данных Pima Indian Diabetes.
from matplotlib import pyplot
from pandas import read_csv
path = r"C:\pima-indians-diabetes.csv"
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=names)
data.plot(kind='density', subplots=True, layout=(3,3), sharex=False)
pyplot.show()Вывод
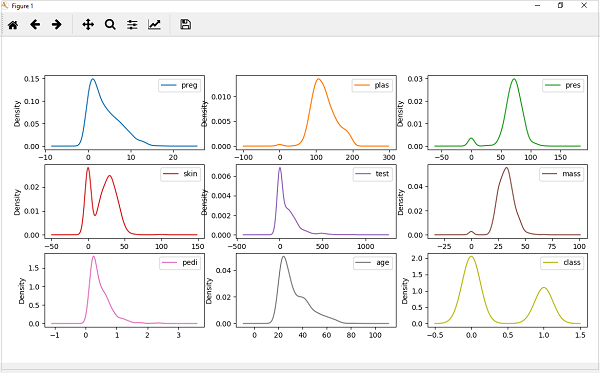
Из вышеприведенного вывода можно легко понять разницу между графиками плотности и гистограммами.
Графики ящиков и усов
Диаграммы ящиков и усов, также называемые кратко ящичками, - еще один полезный метод анализа распределения каждого атрибута. Ниже приведены характеристики этой техники -
Он является одномерным по своей природе и суммирует распределение каждого атрибута.
Он рисует линию для среднего значения, т.е. для медианы.
Он рисует рамку вокруг 25% и 75%.
Он также рисует усы, которые дают нам представление о разбросе данных.
Точки за пределами усов означают выбросы. Значения выбросов будут в 1,5 раза больше, чем размер разброса средних данных.
пример
В следующем примере скрипт Python сгенерирует графики плотности для распределения атрибутов набора данных Pima Indian Diabetes.
from matplotlib import pyplot
from pandas import read_csv
path = r"C:\pima-indians-diabetes.csv"
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=names)
data.plot(kind='box', subplots=True, layout=(3,3), sharex=False,sharey=False)
pyplot.show()Вывод

Из приведенного выше графика распределения атрибутов можно заметить, что возраст, тест и кожа кажутся смещенными в сторону меньших значений.
Многомерные графики: взаимодействие между несколькими переменными
Другой тип визуализации - это многомерная или «многомерная» визуализация. С помощью многомерной визуализации мы можем понять взаимодействие между несколькими атрибутами нашего набора данных. Ниже приведены некоторые методы в Python для реализации многомерной визуализации.
График корреляционной матрицы
Корреляция - это показатель изменений между двумя переменными. В наших предыдущих главах мы обсуждали коэффициенты корреляции Пирсона, а также важность корреляции. Мы можем построить матрицу корреляции, чтобы показать, какая переменная имеет высокую или низкую корреляцию по отношению к другой переменной.
пример
В следующем примере скрипт Python сгенерирует и построит корреляционную матрицу для набора данных Pima Indian Diabetes. Его можно сгенерировать с помощью функции corr () в Pandas DataFrame и построить с помощью pyplot.
from matplotlib import pyplot
from pandas import read_csv
import numpy
Path = r"C:\pima-indians-diabetes.csv"
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(Path, names=names)
correlations = data.corr()
fig = pyplot.figure()
ax = fig.add_subplot(111)
cax = ax.matshow(correlations, vmin=-1, vmax=1)
fig.colorbar(cax)
ticks = numpy.arange(0,9,1)
ax.set_xticks(ticks)
ax.set_yticks(ticks)
ax.set_xticklabels(names)
ax.set_yticklabels(names)
pyplot.show()Вывод

Из вышеприведенного вывода корреляционной матрицы мы можем видеть, что она симметрична, т.е. нижний левый угол совпадает с верхним правым. Также наблюдается, что каждая переменная положительно коррелирует друг с другом.
График матрицы рассеяния
Диаграммы разброса показывают, насколько сильно одна переменная зависит от другой или взаимосвязь между ними, с помощью точек в двух измерениях. Точечные диаграммы очень похожи на линейные графики в том смысле, что они используют горизонтальные и вертикальные оси для построения точек данных.
пример
В следующем примере скрипт Python сгенерирует и построит матрицу разброса для набора данных Pima Indian Diabetes. Его можно сгенерировать с помощью функции scatter_matrix () в Pandas DataFrame и построить с помощью pyplot.
from matplotlib import pyplot
from pandas import read_csv
from pandas.tools.plotting import scatter_matrix
path = r"C:\pima-indians-diabetes.csv"
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=names)
scatter_matrix(data)
pyplot.show()Вывод

Введение
Алгоритмы машинного обучения полностью зависят от данных, потому что это наиболее важный аспект, который делает возможным обучение моделей. С другой стороны, если мы не сможем разобраться в этих данных, прежде чем передать их алгоритмам машинного обучения, машина будет бесполезна. Проще говоря, нам всегда нужно вводить правильные данные, т.е. данные в правильном масштабе, формате и содержащие значимые функции, для проблемы, которую мы хотим, чтобы машина решила.
Это делает подготовку данных наиболее важным шагом в процессе машинного обучения. Подготовку данных можно определить как процедуру, которая делает наш набор данных более подходящим для процесса машинного обучения.
Почему предварительная обработка данных?
После выбора необработанных данных для обучения машинному обучению наиболее важной задачей является предварительная обработка данных. В широком смысле, предварительная обработка данных преобразует выбранные данные в форму, с которой мы можем работать или можем передавать в алгоритмы машинного обучения. Нам всегда нужно предварительно обрабатывать наши данные, чтобы они соответствовали ожиданиям алгоритма машинного обучения.
Методы предварительной обработки данных
У нас есть следующие методы предварительной обработки данных, которые можно применить к набору данных для получения данных для алгоритмов машинного обучения:
Масштабирование
Скорее всего, наш набор данных состоит из атрибутов с разным масштабом, но мы не можем предоставить такие данные для алгоритма машинного обучения, поэтому он требует изменения масштаба. Изменение масштаба данных гарантирует, что атрибуты имеют одинаковый масштаб. Как правило, атрибуты масштабируются в диапазоне от 0 до 1. Алгоритмы ML, такие как градиентный спуск и k-ближайших соседей, требуют масштабированных данных. Мы можем масштабировать данные с помощью класса MinMaxScaler библиотеки Python scikit-learn.
пример
В этом примере мы изменим масштаб данных набора данных диабета индейцев пима, который мы использовали ранее. Сначала будут загружены данные CSV (как это делалось в предыдущих главах), а затем с помощью класса MinMaxScaler они будут масштабированы в диапазоне от 0 до 1.
Первые несколько строк следующего скрипта такие же, как мы писали в предыдущих главах при загрузке данных CSV.
from pandas import read_csv
from numpy import set_printoptions
from sklearn import preprocessing
path = r'C:\pima-indians-diabetes.csv'
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
dataframe = read_csv(path, names=names)
array = dataframe.valuesТеперь мы можем использовать класс MinMaxScaler для изменения масштаба данных в диапазоне от 0 до 1.
data_scaler = preprocessing.MinMaxScaler(feature_range=(0,1))
data_rescaled = data_scaler.fit_transform(array)Мы также можем суммировать данные для вывода по нашему выбору. Здесь мы устанавливаем точность равной 1 и показываем первые 10 строк вывода.
set_printoptions(precision=1)
print ("\nScaled data:\n", data_rescaled[0:10])Вывод
Scaled data:
[[0.4 0.7 0.6 0.4 0. 0.5 0.2 0.5 1. ]
[0.1 0.4 0.5 0.3 0. 0.4 0.1 0.2 0. ]
[0.5 0.9 0.5 0. 0. 0.3 0.3 0.2 1. ]
[0.1 0.4 0.5 0.2 0.1 0.4 0. 0. 0. ]
[0. 0.7 0.3 0.4 0.2 0.6 0.9 0.2 1. ]
[0.3 0.6 0.6 0. 0. 0.4 0.1 0.2 0. ]
[0.2 0.4 0.4 0.3 0.1 0.5 0.1 0.1 1. ]
[0.6 0.6 0. 0. 0. 0.5 0. 0.1 0. ]
[0.1 1. 0.6 0.5 0.6 0.5 0. 0.5 1. ]
[0.5 0.6 0.8 0. 0. 0. 0.1 0.6 1. ]]Из вышеприведенного вывода все данные были масштабированы в диапазоне от 0 до 1.
Нормализация
Еще один полезный метод предварительной обработки данных - нормализация. Это используется для масштабирования каждой строки данных до длины 1. Это в основном полезно в разреженном наборе данных, где у нас много нулей. Мы можем масштабировать данные с помощью класса Normalizer библиотеки Python scikit-learn.
Типы нормализации
В машинном обучении есть два типа методов предварительной обработки нормализации, а именно:
L1 нормализация
Его можно определить как метод нормализации, который изменяет значения набора данных таким образом, чтобы в каждой строке сумма абсолютных значений всегда была до 1. Это также называется наименьшими абсолютными отклонениями.
Example
В этом примере мы используем технику L1 Normalize для нормализации данных набора данных Pima Indians Diabetes, который мы использовали ранее. Сначала будут загружены данные CSV, а затем с помощью класса Normalizer они будут нормализованы.
Первые несколько строк следующего скрипта такие же, как мы писали в предыдущих главах при загрузке данных CSV.
from pandas import read_csv
from numpy import set_printoptions
from sklearn.preprocessing import Normalizer
path = r'C:\pima-indians-diabetes.csv'
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
dataframe = read_csv (path, names=names)
array = dataframe.valuesТеперь мы можем использовать класс Normalizer с L1 для нормализации данных.
Data_normalizer = Normalizer(norm='l1').fit(array)
Data_normalized = Data_normalizer.transform(array)Мы также можем суммировать данные для вывода по нашему выбору. Здесь мы устанавливаем точность равной 2 и показываем первые 3 строки в выводе.
set_printoptions(precision=2)
print ("\nNormalized data:\n", Data_normalized [0:3])Output
Normalized data:
[[0.02 0.43 0.21 0.1 0. 0.1 0. 0.14 0. ]
[0. 0.36 0.28 0.12 0. 0.11 0. 0.13 0. ]
[0.03 0.59 0.21 0. 0. 0.07 0. 0.1 0. ]]L2 нормализация
Его можно определить как метод нормализации, который изменяет значения набора данных таким образом, чтобы в каждой строке сумма квадратов всегда была до 1. Это также называется методом наименьших квадратов.
Example
В этом примере мы используем технику L2 нормализации для нормализации данных набора данных диабета индейцев пима, который мы использовали ранее. Сначала будут загружены данные CSV (как это делалось в предыдущих главах), а затем с помощью класса Normalizer они будут нормализованы.
Первые несколько строк следующего скрипта такие же, как мы писали в предыдущих главах при загрузке данных CSV.
from pandas import read_csv
from numpy import set_printoptions
from sklearn.preprocessing import Normalizer
path = r'C:\pima-indians-diabetes.csv'
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
dataframe = read_csv (path, names=names)
array = dataframe.valuesТеперь мы можем использовать класс Normalizer с L1 для нормализации данных.
Data_normalizer = Normalizer(norm='l2').fit(array)
Data_normalized = Data_normalizer.transform(array)Мы также можем суммировать данные для вывода по нашему выбору. Здесь мы устанавливаем точность равной 2 и показываем первые 3 строки в выводе.
set_printoptions(precision=2)
print ("\nNormalized data:\n", Data_normalized [0:3])Output
Normalized data:
[[0.03 0.83 0.4 0.2 0. 0.19 0. 0.28 0.01]
[0.01 0.72 0.56 0.24 0. 0.22 0. 0.26 0. ]
[0.04 0.92 0.32 0. 0. 0.12 0. 0.16 0.01]]Бинаризация
Как следует из названия, это метод, с помощью которого мы можем сделать наши данные двоичными. Мы можем использовать двоичный порог, чтобы сделать наши данные двоичными. Значения выше этого порогового значения будут преобразованы в 1, а значения ниже этого порога будут преобразованы в 0. Например, если мы выберем пороговое значение = 0,5, тогда значение набора данных выше него станет 1, а ниже этого станет 0. То есть почему мы можем это назватьbinarizing данные или thresholdingданные. Этот метод полезен, когда у нас есть вероятности в нашем наборе данных и мы хотим преобразовать их в четкие значения.
Мы можем преобразовать данные в двоичную форму с помощью класса Binarizer библиотеки Python scikit-learn.
пример
В этом примере мы изменим масштаб данных набора данных диабета индейцев пима, который мы использовали ранее. Сначала будут загружены данные CSV, а затем с помощью класса Binarizer они будут преобразованы в двоичные значения, т.е. 0 и 1 в зависимости от порогового значения. Мы берем 0,5 в качестве порогового значения.
Первые несколько строк следующего скрипта такие же, как мы писали в предыдущих главах при загрузке данных CSV.
from pandas import read_csv
from sklearn.preprocessing import Binarizer
path = r'C:\pima-indians-diabetes.csv'
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
dataframe = read_csv(path, names=names)
array = dataframe.valuesТеперь мы можем использовать класс Binarize для преобразования данных в двоичные значения.
binarizer = Binarizer(threshold=0.5).fit(array)
Data_binarized = binarizer.transform(array)Здесь мы показываем первые 5 строк вывода.
print ("\nBinary data:\n", Data_binarized [0:5])Вывод
Binary data:
[[1. 1. 1. 1. 0. 1. 1. 1. 1.]
[1. 1. 1. 1. 0. 1. 0. 1. 0.]
[1. 1. 1. 0. 0. 1. 1. 1. 1.]
[1. 1. 1. 1. 1. 1. 0. 1. 0.]
[0. 1. 1. 1. 1. 1. 1. 1. 1.]]Стандартизация
Еще один полезный метод предварительной обработки данных, который в основном используется для преобразования атрибутов данных с распределением Гаусса. Он отличает среднее значение и SD (стандартное отклонение) от стандартного распределения Гаусса со средним значением 0 и SD, равным 1. Этот метод полезен в алгоритмах машинного обучения, таких как линейная регрессия, логистическая регрессия, которая предполагает распределение Гаусса во входном наборе данных и дает лучший результат. результаты с измененными данными. Мы можем стандартизировать данные (среднее значение = 0 и SD = 1) с помощью класса StandardScaler библиотеки Python scikit-learn.
пример
В этом примере мы изменим масштаб данных набора данных диабета индейцев пима, который мы использовали ранее. Сначала будут загружены данные CSV, а затем с помощью класса StandardScaler они будут преобразованы в распределение по Гауссу со средним значением = 0 и SD = 1.
Первые несколько строк следующего скрипта такие же, как мы писали в предыдущих главах при загрузке данных CSV.
from sklearn.preprocessing import StandardScaler
from pandas import read_csv
from numpy import set_printoptions
path = r'C:\pima-indians-diabetes.csv'
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
dataframe = read_csv(path, names=names)
array = dataframe.valuesТеперь мы можем использовать класс StandardScaler для изменения масштаба данных.
data_scaler = StandardScaler().fit(array)
data_rescaled = data_scaler.transform(array)Мы также можем суммировать данные для вывода по нашему выбору. Здесь мы устанавливаем точность равной 2 и показываем первые 5 строк вывода.
set_printoptions(precision=2)
print ("\nRescaled data:\n", data_rescaled [0:5])Вывод
Rescaled data:
[[ 0.64 0.85 0.15 0.91 -0.69 0.2 0.47 1.43 1.37]
[-0.84 -1.12 -0.16 0.53 -0.69 -0.68 -0.37 -0.19 -0.73]
[ 1.23 1.94 -0.26 -1.29 -0.69 -1.1 0.6 -0.11 1.37]
[-0.84 -1. -0.16 0.15 0.12 -0.49 -0.92 -1.04 -0.73]
[-1.14 0.5 -1.5 0.91 0.77 1.41 5.48 -0.02 1.37]]Маркировка данных
Мы обсудили важность хороших данных для алгоритмов машинного обучения, а также некоторые методы предварительной обработки данных перед их отправкой в алгоритмы машинного обучения. Еще один аспект в этом отношении - разметка данных. Также очень важно отправлять данные в алгоритмы машинного обучения с правильной маркировкой. Например, в случае проблем с классификацией на данных имеется множество меток в виде слов, чисел и т. Д.
Что такое кодирование меток?
Большинство функций sklearn ожидают, что данные будут иметь числовые метки, а не слова. Следовательно, нам необходимо преобразовать такие метки в числовые. Этот процесс называется кодированием метки. Мы можем выполнить кодирование меток данных с помощью функции LabelEncoder () библиотеки Python scikit-learn.
пример
В следующем примере скрипт Python выполнит кодирование меток.
Сначала импортируйте необходимые библиотеки Python следующим образом:
import numpy as np
from sklearn import preprocessingТеперь нам нужно предоставить метки ввода следующим образом:
input_labels = ['red','black','red','green','black','yellow','white']Следующая строка кода создаст кодировщик меток и обучит его.
encoder = preprocessing.LabelEncoder()
encoder.fit(input_labels)Следующие строки скрипта будут проверять производительность, кодируя случайный упорядоченный список -
test_labels = ['green','red','black']
encoded_values = encoder.transform(test_labels)
print("\nLabels =", test_labels)
print("Encoded values =", list(encoded_values))
encoded_values = [3,0,4,1]
decoded_list = encoder.inverse_transform(encoded_values)Мы можем получить список закодированных значений с помощью следующего скрипта Python -
print("\nEncoded values =", encoded_values)
print("\nDecoded labels =", list(decoded_list))Вывод
Labels = ['green', 'red', 'black']
Encoded values = [1, 2, 0]
Encoded values = [3, 0, 4, 1]
Decoded labels = ['white', 'black', 'yellow', 'green']В предыдущей главе мы подробно рассмотрели, как предварительно обработать и подготовить данные для машинного обучения. В этой главе давайте подробно разберемся с выбором функций данных и различными аспектами, связанными с этим.
Важность выбора характеристик данных
Производительность модели машинного обучения прямо пропорциональна характеристикам данных, используемым для ее обучения. На производительность модели машинного обучения будет оказано негативное влияние, если предоставленные ей функции данных не будут иметь значения. С другой стороны, использование соответствующих функций данных может повысить точность вашей модели машинного обучения, особенно линейной и логистической регрессии.
Теперь возникает вопрос, что такое автоматический выбор функции? Его можно определить как процесс, с помощью которого мы выбираем те характеристики в наших данных, которые наиболее релевантны выходным или прогнозируемым переменным, в которых мы заинтересованы. Это также называется выбором атрибута.
Ниже приведены некоторые из преимуществ автоматического выбора функций перед моделированием данных.
Выполнение выбора функций перед моделированием данных уменьшит переоснащение.
Выполнение выбора функций перед моделированием данных повысит точность модели машинного обучения.
Выполнение выбора функций перед моделированием данных сократит время обучения
Методы выбора функций
Ниже приведены методы автоматического выбора функций, которые мы можем использовать для моделирования данных машинного обучения в Python.
Одномерный выбор
Этот метод выбора характеристик очень полезен при выборе тех характеристик с помощью статистического тестирования, которые имеют наиболее тесную связь с переменными прогноза. Мы можем реализовать метод одномерного выбора функций с помощью SelectKBest0class библиотеки Python scikit-learn.
Example
В этом примере мы будем использовать набор данных диабета индейцев пима, чтобы выбрать 4 атрибута, обладающих лучшими характеристиками, с помощью статистического теста хи-квадрат.
from pandas import read_csv
from numpy import set_printoptions
from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import chi2
path = r'C:\pima-indians-diabetes.csv'
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
dataframe = read_csv(path, names=names)
array = dataframe.valuesДалее мы разделим массив на компоненты ввода и вывода -
X = array[:,0:8]
Y = array[:,8]Следующие строки кода выберут лучшие функции из набора данных -
test = SelectKBest(score_func=chi2, k=4)
fit = test.fit(X,Y)Мы также можем суммировать данные для вывода по нашему выбору. Здесь мы устанавливаем точность равной 2 и показываем 4 атрибута данных с лучшими функциями вместе с лучшим результатом для каждого атрибута -
set_printoptions(precision=2)
print(fit.scores_)
featured_data = fit.transform(X)
print ("\nFeatured data:\n", featured_data[0:4])Output
[ 111.52 1411.89 17.61 53.11 2175.57 127.67 5.39 181.3 ]
Featured data:
[[148. 0. 33.6 50. ]
[ 85. 0. 26.6 31. ]
[183. 0. 23.3 32. ]
[ 89. 94. 28.1 21. ]]Рекурсивное исключение признаков
Как следует из названия, метод выбора функций RFE (рекурсивное исключение признаков) удаляет атрибуты рекурсивно и строит модель с оставшимися атрибутами. Мы можем реализовать технику выбора функций RFE с помощью класса RFE библиотеки Python scikit-learn.
пример
В этом примере мы будем использовать RFE с алгоритмом логистической регрессии, чтобы выбрать 3 лучших атрибута с лучшими характеристиками из набора данных Pima Indians Diabetes до.
from pandas import read_csv
from sklearn.feature_selection import RFE
from sklearn.linear_model import LogisticRegression
path = r'C:\pima-indians-diabetes.csv'
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
dataframe = read_csv(path, names=names)
array = dataframe.valuesЗатем мы разделим массив на его входные и выходные компоненты -
X = array[:,0:8]
Y = array[:,8]Следующие строки кода выберут лучшие функции из набора данных:
model = LogisticRegression()
rfe = RFE(model, 3)
fit = rfe.fit(X, Y)
print("Number of Features: %d")
print("Selected Features: %s")
print("Feature Ranking: %s")Вывод
Number of Features: 3
Selected Features: [ True False False False False True True False]
Feature Ranking: [1 2 3 5 6 1 1 4]Как видно из результатов выше, RFE выбирает preg, mass и pedi в качестве первых трех лучших характеристик. На выходе они отмечены цифрой 1.
Анализ главных компонентов (PCA)
PCA, обычно называемый методом сокращения данных, является очень полезным методом выбора функций, поскольку он использует линейную алгебру для преобразования набора данных в сжатую форму. Мы можем реализовать технику выбора функций PCA с помощью класса PCA библиотеки Python scikit-learn. Мы можем выбрать количество основных компонентов на выходе.
пример
В этом примере мы будем использовать PCA для выбора 3 лучших основных компонентов из набора данных диабета индейцев пима.
from pandas import read_csv
from sklearn.decomposition import PCA
path = r'C:\pima-indians-diabetes.csv'
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
dataframe = read_csv(path, names=names)
array = dataframe.valuesДалее мы разделим массив на компоненты ввода и вывода -
X = array[:,0:8]
Y = array[:,8]Следующие строки кода будут извлекать функции из набора данных -
pca = PCA(n_components=3)
fit = pca.fit(X)
print("Explained Variance: %s") % fit.explained_variance_ratio_
print(fit.components_)Вывод
Explained Variance: [ 0.88854663 0.06159078 0.02579012]
[[ -2.02176587e-03 9.78115765e-02 1.60930503e-02 6.07566861e-02
9.93110844e-01 1.40108085e-02 5.37167919e-04 -3.56474430e-03]
[ 2.26488861e-02 9.72210040e-01 1.41909330e-01 -5.78614699e-02
-9.46266913e-02 4.69729766e-02 8.16804621e-04 1.40168181e-01]
[ -2.24649003e-02 1.43428710e-01 -9.22467192e-01 -3.07013055e-01
2.09773019e-02 -1.32444542e-01 -6.39983017e-04 -1.25454310e-01]]Из вышеприведенных результатов видно, что 3 основных компонента мало похожи на исходные данные.
Важность функции
Как следует из названия, для выбора важных характеристик используется метод важности. Он в основном использует обученный контролируемый классификатор для выбора функций. Мы можем реализовать эту технику выбора функций с помощью класса ExtraTreeClassifier библиотеки Python scikit-learn.
пример
В этом примере мы будем использовать ExtraTreeClassifier для выбора функций из набора данных Pima Indians Diabetes.
from pandas import read_csv
from sklearn.ensemble import ExtraTreesClassifier
path = r'C:\Desktop\pima-indians-diabetes.csv'
names = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
dataframe = read_csv(data, names=names)
array = dataframe.valuesДалее мы разделим массив на компоненты ввода и вывода -
X = array[:,0:8]
Y = array[:,8]Следующие строки кода будут извлекать функции из набора данных -
model = ExtraTreesClassifier()
model.fit(X, Y)
print(model.feature_importances_)Вывод
[ 0.11070069 0.2213717 0.08824115 0.08068703 0.07281761 0.14548537 0.12654214 0.15415431]Из выходных данных мы можем видеть, что есть оценки для каждого атрибута. Чем выше оценка, тем выше важность этого атрибута.
Введение в классификацию
Классификацию можно определить как процесс прогнозирования класса или категории на основе наблюдаемых значений или заданных точек данных. Вывод по категориям может иметь вид «черный» или «белый», «спам» или «без спама».
Математически классификация - это задача аппроксимации функции отображения (f) входных переменных (X) в выходные переменные (Y). В основном это относится к контролируемому машинному обучению, в котором цели также предоставляются вместе с набором входных данных.
Примером проблемы классификации может быть обнаружение спама в электронных письмах. Может быть только две категории вывода: «спам» и «нет спама»; следовательно, это классификация бинарного типа.
Чтобы реализовать эту классификацию, нам сначала нужно обучить классификатор. В этом примере в качестве обучающих данных будут использоваться электронные письма «спам» и «без спама». После успешного обучения классификатора его можно использовать для обнаружения неизвестного адреса электронной почты.
Типы учащихся в классификации
У нас есть два типа учеников в зависимости от задач классификации:
Ленивые ученики
Как следует из названия, такие ученики ждут появления данных тестирования после сохранения данных обучения. Классификация проводится только после получения данных тестирования. Они тратят меньше времени на тренировки, но больше на прогнозы. Примеры ленивых учеников - это K-ближайший сосед и рассуждения на основе случая.
Активные ученики
В отличие от ленивых учеников, активные ученики создают модель классификации, не дожидаясь появления данных тестирования после сохранения данных обучения. Они тратят больше времени на тренировки, но меньше на прогнозы. Примерами активных учеников являются деревья принятия решений, наивный байесовский метод и искусственные нейронные сети (ИНС).
Построение классификатора на Python
Scikit-learn, библиотеку Python для машинного обучения можно использовать для создания классификатора на Python. Шаги для создания классификатора в Python следующие:
Шаг 1. Импорт необходимого пакета Python
Для создания классификатора с использованием scikit-learn нам нужно его импортировать. Мы можем импортировать его, используя следующий скрипт -
import sklearnШаг 2. Импорт набора данных
После импорта необходимого пакета нам понадобится набор данных для построения модели прогнозирования классификации. Мы можем импортировать его из набора данных sklearn или использовать другой в соответствии с нашими требованиями. Мы собираемся использовать диагностическую базу данных рака молочной железы sklearn, штат Висконсин. Мы можем импортировать его с помощью следующего скрипта -
from sklearn.datasets import load_breast_cancerСледующий скрипт загрузит набор данных;
data = load_breast_cancer()Нам также необходимо организовать данные, и это можно сделать с помощью следующих скриптов:
label_names = data['target_names']
labels = data['target']
feature_names = data['feature_names']
features = data['data']Следующая команда напечатает названия ярлыков, «злокачественный» и «доброкачественный» в случае нашей базы данных.
print(label_names)Результатом вышеуказанной команды являются имена меток -
['malignant' 'benign']Эти метки отображаются на двоичные значения 0 и 1. Malignant рак представлен 0 и Benign рак представлен 1.
Имена функций и значения функций этих меток можно увидеть с помощью следующих команд:
print(feature_names[0])Результатом вышеуказанной команды являются имена функций для метки 0, т.е. Malignant рак -
mean radiusТочно так же названия функций для этикетки могут быть произведены следующим образом:
print(feature_names[1])Результатом вышеуказанной команды являются имена функций для метки 1, т.е. Benign рак -
mean textureМы можем распечатать характеристики этих этикеток с помощью следующей команды -
print(features[0])Это даст следующий результат -
[1.799e+01 1.038e+01 1.228e+02 1.001e+03 1.184e-01 2.776e-01 3.001e-01
1.471e-01 2.419e-01 7.871e-02 1.095e+00 9.053e-01 8.589e+00 1.534e+02
6.399e-03 4.904e-02 5.373e-02 1.587e-02 3.003e-02 6.193e-03 2.538e+01
1.733e+01 1.846e+02 2.019e+03 1.622e-01 6.656e-01 7.119e-01 2.654e-01
4.601e-01 1.189e-01]Мы можем распечатать характеристики этих этикеток с помощью следующей команды -
print(features[1])Это даст следующий результат -
[2.057e+01 1.777e+01 1.329e+02 1.326e+03 8.474e-02 7.864e-02 8.690e-02
7.017e-02 1.812e-01 5.667e-02 5.435e-01 7.339e-01 3.398e+00 7.408e+01
5.225e-03 1.308e-02 1.860e-02 1.340e-02 1.389e-02 3.532e-03 2.499e+01
2.341e+01 1.588e+02 1.956e+03 1.238e-01 1.866e-01 2.416e-01 1.860e-01
2.750e-01 8.902e-02]Шаг 3. Организация данных в наборы для обучения и тестирования
Поскольку нам нужно протестировать нашу модель на невидимых данных, мы разделим наш набор данных на две части: обучающий набор и тестовый набор. Мы можем использовать функцию train_test_split () пакета python sklearn для разделения данных на наборы. Следующая команда импортирует функцию -
from sklearn.model_selection import train_test_splitТеперь следующая команда разделит данные на данные обучения и тестирования. В этом примере мы используем 40 процентов данных для целей тестирования и 60 процентов данных для целей обучения -
train, test, train_labels, test_labels = train_test_split(features,labels,test_size = 0.40, random_state = 42)Шаг 4 - Оценка модели
После разделения данных на обучение и тестирование нам нужно построить модель. Для этого мы будем использовать алгоритм Наивного Байеса. Следующие команды импортируют модуль GaussianNB -
from sklearn.naive_bayes import GaussianNBТеперь инициализируйте модель следующим образом -
gnb = GaussianNB()Затем с помощью следующей команды мы можем обучить модель -
model = gnb.fit(train, train_labels)Теперь для оценки нам нужно сделать прогнозы. Это можно сделать с помощью функции predic () следующим образом:
preds = gnb.predict(test)
print(preds)Это даст следующий результат -
[1 0 0 1 1 0 0 0 1 1 1 0 1 0 1 0 1 1 1 0 1 1 0 1 1 1 1 1 1 0 1 1 1 1 1 1 0
1 0 1 1 0 1 1 1 1 1 1 1 1 0 0 1 1 1 1 1 0 0 1 1 0 0 1 1 1 0 0 1 1 0 0 1 0
1 1 1 1 1 1 0 1 1 0 0 0 0 0 1 1 1 1 1 1 1 1 0 0 1 0 0 1 0 0 1 1 1 0 1 1 0
1 1 0 0 0 1 1 1 0 0 1 1 0 1 0 0 1 1 0 0 0 1 1 1 0 1 1 0 0 1 0 1 1 0 1 0 0
1 1 1 1 1 1 1 0 0 1 1 1 1 1 1 1 1 1 1 1 1 0 1 1 1 0 1 1 0 1 1 1 1 1 1 0 0
0 1 1 0 1 0 1 1 1 1 0 1 1 0 1 1 1 0 1 0 0 1 1 1 1 1 1 1 1 0 1 1 1 1 1 0 1
0 0 1 1 0 1]Вышеупомянутые серии из 0 и 1 на выходе являются прогнозируемыми значениями для Malignant и Benign классы опухолей.
Шаг 5- Определение точности
Мы можем определить точность построения модели на предыдущем шаге, сравнив два массива, а именно test_labels и preds. Мы будем использовать функцию precision_score (), чтобы определить точность.
from sklearn.metrics import accuracy_score
print(accuracy_score(test_labels,preds))
0.951754385965Приведенный выше результат показывает, что классификатор NaïveBayes имеет точность 95,17%.
Метрики оценки классификации
Работа не выполняется, даже если вы завершили реализацию приложения или модели машинного обучения. Мы должны выяснить, насколько эффективна наша модель? Могут быть разные метрики оценки, но мы должны выбирать их внимательно, потому что выбор метрик влияет на то, как измеряется и сравнивается производительность алгоритма машинного обучения.
Ниже приведены некоторые из важных показателей оценки классификации, среди которых вы можете выбрать в зависимости от набора данных и типа проблемы.
Матрица путаницы
Это самый простой способ измерить производительность задачи классификации, когда выходные данные могут относиться к классам двух или более типов. Матрица путаницы - это не что иное, как таблица с двумя измерениями, а именно. «Фактический» и «Прогнозируемый» и, кроме того, оба измерения имеют «Истинные положительные результаты (TP)», «Истинные отрицательные результаты (TN)», «Ложные положительные результаты (FP)», «Ложные отрицательные результаты (FN)», как показано ниже -

True Positives (TP) - Это тот случай, когда и фактический класс, и прогнозируемый класс точки данных равны 1.
True Negatives (TN) - Это тот случай, когда как фактический, так и прогнозируемый класс точки данных равны 0.
False Positives (FP) - Это тот случай, когда фактический класс точки данных равен 0, а прогнозируемый класс точки данных равен 1.
False Negatives (FN) - Это тот случай, когда фактический класс точки данных равен 1, а прогнозируемый класс точки данных равен 0.
Мы можем найти матрицу путаницы с помощью функции confusion_matrix () программы sklearn. С помощью следующего скрипта мы можем найти матрицу путаницы выше построенного двоичного классификатора -
from sklearn.metrics import confusion_matrixВывод
[[ 73 7]
[ 4 144]]Точность
Его можно определить как количество правильных прогнозов, сделанных нашей моделью машинного обучения. Мы можем легко вычислить его по матрице путаницы с помощью следующей формулы -
$$=\frac{+}{+++}$$Для построенного выше двоичного классификатора TP + TN = 73 + 144 = 217 и TP + FP + FN + TN = 73 + 7 + 4 + 144 = 228.
Следовательно, точность = 217/228 = 0,951754385965, что такое же, как мы рассчитали после создания нашего двоичного классификатора.
Точность
Точность, используемая при поиске документов, может быть определена как количество правильных документов, возвращаемых нашей моделью машинного обучения. Мы можем легко вычислить его по матрице путаницы с помощью следующей формулы -
$$=\frac{}{+FP}$$Для построенного выше двоичного классификатора TP = 73 и TP + FP = 73 + 7 = 80.
Следовательно, точность = 73/80 = 0,915.
Отзыв или чувствительность
Отзыв можно определить как количество положительных результатов, возвращаемых нашей моделью машинного обучения. Мы можем легко вычислить его по матрице путаницы с помощью следующей формулы -
$$=\frac{}{+FN}$$Для построенного выше двоичного классификатора TP = 73 и TP + FN = 73 + 4 = 77.
Следовательно, точность = 73/77 = 0,94805.
Специфика
Специфичность, в отличие от отзыва, может быть определена как количество негативов, возвращаемых нашей моделью машинного обучения. Мы можем легко вычислить его по матрице путаницы с помощью следующей формулы -
$$=\frac{N}{N+FP}$$Для построенного выше двоичного классификатора TN = 144 и TN + FP = 144 + 7 = 151.
Следовательно, точность = 144/151 = 0,95364.
Различные алгоритмы классификации ML
Ниже приведены некоторые важные алгоритмы классификации ML:
Логистическая регрессия
Машина опорных векторов (SVM)
Древо решений
Наивный байесовский
Случайный лес
Мы подробно обсудим все эти алгоритмы классификации в следующих главах.
Приложения
Некоторые из наиболее важных приложений алгоритмов классификации следующие:
Распознавание речи
Распознавание почерка
Биометрическая идентификация
Классификация документов
Введение в логистическую регрессию
Логистическая регрессия - это алгоритм классификации с контролируемым обучением, используемый для прогнозирования вероятности целевой переменной. Природа целевой или зависимой переменной является дихотомической, что означает, что может быть только два возможных класса.
Проще говоря, зависимая переменная имеет двоичную природу, а данные закодированы как 1 (означает успех / да) или 0 (означает сбой / нет).
Математически модель логистической регрессии предсказывает P (Y = 1) как функцию от X. Это один из простейших алгоритмов машинного обучения, который можно использовать для различных задач классификации, таких как обнаружение спама, прогнозирование диабета, обнаружение рака и т. Д.
Типы логистической регрессии
Как правило, логистическая регрессия означает двоичную логистическую регрессию, имеющую двоичные целевые переменные, но могут быть еще две категории целевых переменных, которые можно предсказать с ее помощью. Основываясь на этом количестве категорий, логистическую регрессию можно разделить на следующие типы:
Двоичный или биномиальный
В такой классификации зависимая переменная будет иметь только два возможных типа: 1 и 0. Например, эти переменные могут представлять успех или неудачу, да или нет, победу или поражение и т. Д.
Полиномиальный
В такой классификации зависимая переменная может иметь 3 или более возможных неупорядоченных типа или типы, не имеющие количественной значимости. Например, эти переменные могут представлять «Тип A», «Тип B» или «Тип C».
Порядковый
В такой классификации зависимая переменная может иметь 3 или более возможных упорядоченных типа или типов, имеющих количественное значение. Например, эти переменные могут представлять «плохо» или «хорошо», «очень хорошо», «отлично», и каждая категория может иметь такие баллы, как 0,1,2,3.
Допущения логистической регрессии
Прежде чем погрузиться в реализацию логистической регрессии, мы должны знать о следующих предположениях о том же:
В случае бинарной логистической регрессии целевые переменные всегда должны быть бинарными, а желаемый результат представлен уровнем фактора 1.
В модели не должно быть мультиколлинеарности, что означает, что независимые переменные должны быть независимыми друг от друга.
Мы должны включить в нашу модель значимые переменные.
Мы должны выбрать большой размер выборки для логистической регрессии.
Модель бинарной логистической регрессии
Простейшей формой логистической регрессии является бинарная или биномиальная логистическая регрессия, в которой целевая или зависимая переменная может иметь только 2 возможных типа: 1 или 0. Это позволяет нам моделировать взаимосвязь между несколькими переменными-предикторами и бинарной / биномиальной целевой переменной. В случае логистической регрессии линейная функция в основном используется как вход для другой функции, например, в следующем соотношении:
$h_{\theta}{(x)}=g(\theta^{T}x)ℎ 0≤h_{\theta}≤1$Вот логистическая или сигмовидная функция, которую можно задать следующим образом:
$g(z)= \frac{1}{1+e^{-z}}ℎ =\theta ^{T}$Сигмовидную кривую можно представить с помощью следующего графика. Мы можем видеть, что значения оси Y лежат между 0 и 1 и пересекают ось на 0,5.

Классы можно разделить на положительные и отрицательные. Выходной сигнал относится к классу вероятности положительного, если он находится между 0 и 1. Для нашей реализации мы интерпретируем выход функции гипотезы как положительный, если он равен ≥0,5, в противном случае - отрицательный.
Нам также необходимо определить функцию потерь, чтобы измерить, насколько хорошо алгоритм работает с использованием весов функций, представленных тета следующим образом:
ℎ = ()
$J(\theta) = \frac{1}{m}.(-y^{T}log(h) - (1 -y)^Tlog(1-h))$Теперь, после определения функции потерь, наша основная цель - минимизировать функцию потерь. Это можно сделать с помощью подгонки весов, то есть увеличения или уменьшения веса. С помощью производных функции потерь по каждому весу мы сможем узнать, какие параметры должны иметь больший вес, а какие - меньший.
Следующее уравнение градиентного спуска говорит нам, как изменится потеря, если мы изменим параметры -
$\frac{()}{\theta_{j}}=\frac{1}{m}X^{T}(()−)$Реализация на Python
Теперь мы реализуем описанную выше концепцию биномиальной логистической регрессии в Python. Для этой цели мы используем многомерный набор данных о цветах с именем «iris», который имеет 3 класса по 50 экземпляров в каждом, но мы будем использовать первые два столбца функций. Каждый класс представляет собой разновидность цветка ириса.
Во-первых, нам нужно импортировать необходимые библиотеки следующим образом:
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn import datasetsЗатем загрузите набор данных радужной оболочки следующим образом -
iris = datasets.load_iris()
X = iris.data[:, :2]
y = (iris.target != 0) * 1Мы можем построить наши обучающие данные следующим образом:
plt.figure(figsize=(6, 6))
plt.scatter(X[y == 0][:, 0], X[y == 0][:, 1], color='g', label='0')
plt.scatter(X[y == 1][:, 0], X[y == 1][:, 1], color='y', label='1')
plt.legend();
Затем мы определим сигмовидную функцию, функцию потерь и спуск градиента следующим образом:
class LogisticRegression:
def __init__(self, lr=0.01, num_iter=100000, fit_intercept=True, verbose=False):
self.lr = lr
self.num_iter = num_iter
self.fit_intercept = fit_intercept
self.verbose = verbose
def __add_intercept(self, X):
intercept = np.ones((X.shape[0], 1))
return np.concatenate((intercept, X), axis=1)
def __sigmoid(self, z):
return 1 / (1 + np.exp(-z))
def __loss(self, h, y):
return (-y * np.log(h) - (1 - y) * np.log(1 - h)).mean()
def fit(self, X, y):
if self.fit_intercept:
X = self.__add_intercept(X)Теперь инициализируйте веса следующим образом:
self.theta = np.zeros(X.shape[1])
for i in range(self.num_iter):
z = np.dot(X, self.theta)
h = self.__sigmoid(z)
gradient = np.dot(X.T, (h - y)) / y.size
self.theta -= self.lr * gradient
z = np.dot(X, self.theta)
h = self.__sigmoid(z)
loss = self.__loss(h, y)
if(self.verbose ==True and i % 10000 == 0):
print(f'loss: {loss} \t')С помощью следующего скрипта мы можем предсказать вероятности вывода -
def predict_prob(self, X):
if self.fit_intercept:
X = self.__add_intercept(X)
return self.__sigmoid(np.dot(X, self.theta))
def predict(self, X):
return self.predict_prob(X).round()Затем мы можем оценить модель и построить ее следующим образом:
model = LogisticRegression(lr=0.1, num_iter=300000)
preds = model.predict(X)
(preds == y).mean()
plt.figure(figsize=(10, 6))
plt.scatter(X[y == 0][:, 0], X[y == 0][:, 1], color='g', label='0')
plt.scatter(X[y == 1][:, 0], X[y == 1][:, 1], color='y', label='1')
plt.legend()
x1_min, x1_max = X[:,0].min(), X[:,0].max(),
x2_min, x2_max = X[:,1].min(), X[:,1].max(),
xx1, xx2 = np.meshgrid(np.linspace(x1_min, x1_max), np.linspace(x2_min, x2_max))
grid = np.c_[xx1.ravel(), xx2.ravel()]
probs = model.predict_prob(grid).reshape(xx1.shape)
plt.contour(xx1, xx2, probs, [0.5], linewidths=1, colors='red');
Модель полиномиальной логистической регрессии
Другой полезной формой логистической регрессии является полиномиальная логистическая регрессия, в которой целевая или зависимая переменная может иметь 3 или более возможных неупорядоченных типа, то есть типы, не имеющие количественной значимости.
Реализация на Python
Теперь мы реализуем описанную выше концепцию полиномиальной логистической регрессии в Python. Для этого мы используем набор данных из sklearn с именем digit.
Во-первых, нам нужно импортировать необходимые библиотеки следующим образом:
Import sklearn
from sklearn import datasets
from sklearn import linear_model
from sklearn import metrics
from sklearn.model_selection import train_test_splitЗатем нам нужно загрузить набор цифровых данных -
digits = datasets.load_digits()Теперь определите матрицу признаков (X) и вектор ответа (y) следующим образом:
X = digits.data
y = digits.targetС помощью следующей строки кода мы можем разделить X и y на наборы для обучения и тестирования -
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.4, random_state=1)Теперь создайте объект логистической регрессии следующим образом:
digreg = linear_model.LogisticRegression()Теперь нам нужно обучить модель, используя обучающие наборы следующим образом:
digreg.fit(X_train, y_train)Затем сделайте прогнозы на тестовом наборе следующим образом:
y_pred = digreg.predict(X_test)Затем распечатайте точность модели следующим образом -
print("Accuracy of Logistic Regression model is:",
metrics.accuracy_score(y_test, y_pred)*100)Вывод
Accuracy of Logistic Regression model is: 95.6884561891516Из вышеприведенного вывода мы видим, что точность нашей модели составляет около 96 процентов.
Введение в SVM
Машины опорных векторов (SVM) - это мощные, но гибкие алгоритмы машинного обучения с учителем, которые используются как для классификации, так и для регрессии. Но обычно они используются в задачах классификации. В 1960-х годах SVM были впервые представлены, но позже они были усовершенствованы в 1990 году. SVM имеют свой уникальный способ реализации по сравнению с другими алгоритмами машинного обучения. В последнее время они чрезвычайно популярны из-за их способности обрабатывать несколько непрерывных и категориальных переменных.
Работа SVM
Модель SVM - это в основном представление различных классов в гиперплоскости в многомерном пространстве. Гиперплоскость будет генерироваться SVM итеративно, чтобы можно было минимизировать ошибку. Цель SVM - разделить наборы данных на классы, чтобы найти максимальную маргинальную гиперплоскость (MMH).

Следующие важные концепции в SVM -
Support Vectors- Точки данных, которые находятся ближе всего к гиперплоскости, называются опорными векторами. Разделительная линия будет определена с помощью этих точек данных.
Hyperplane - Как мы видим на приведенной выше диаграмме, это плоскость решения или пространство, которое разделено между набором объектов, имеющих разные классы.
Margin- Его можно определить как разрыв между двумя линиями на точках данных шкафа разных классов. Его можно рассчитать как перпендикулярное расстояние от линии до опорных векторов. Большая маржа считается хорошей маржей, а небольшая маржа - плохой.
Основная цель SVM - разделить наборы данных на классы, чтобы найти максимальную маргинальную гиперплоскость (MMH), и это можно сделать в следующих двух шагах:
Во-первых, SVM будет итеративно генерировать гиперплоскости, что наилучшим образом разделяет классы.
Затем он выберет гиперплоскость, которая правильно разделяет классы.
Реализация SVM на Python
Для реализации SVM в Python мы начнем с импорта стандартных библиотек следующим образом:
import numpy as np
import matplotlib.pyplot as plt
from scipy import stats
import seaborn as sns; sns.set()Затем мы создаем образец набора данных с линейно разделяемыми данными из sklearn.dataset.sample_generator для классификации с использованием SVM -
from sklearn.datasets.samples_generator import make_blobs
X, y = make_blobs(n_samples=100, centers=2,
random_state=0, cluster_std=0.50)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='summer');Следующее будет выходом после создания набора образцов данных, состоящего из 100 образцов и 2 кластеров:

Мы знаем, что SVM поддерживает дискриминационную классификацию. он отделяет классы друг от друга, просто находя линию в случае двух измерений или многообразие в случае нескольких измерений. Он реализован в приведенном выше наборе данных следующим образом:
xfit = np.linspace(-1, 3.5)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='summer')
plt.plot([0.6], [2.1], 'x', color='black', markeredgewidth=4, markersize=12)
for m, b in [(1, 0.65), (0.5, 1.6), (-0.2, 2.9)]:
plt.plot(xfit, m * xfit + b, '-k')
plt.xlim(-1, 3.5);Результат выглядит следующим образом -

Из вышеприведенного вывода видно, что есть три разных разделителя, которые отлично различают вышеуказанные образцы.
Как обсуждалось, основная цель SVM - разделить наборы данных на классы, чтобы найти максимальную граничную гиперплоскость (MMH), поэтому вместо того, чтобы рисовать нулевую линию между классами, мы можем нарисовать вокруг каждой линии поле некоторой ширины до ближайшей точки. Это можно сделать следующим образом -
xfit = np.linspace(-1, 3.5)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='summer')
for m, b, d in [(1, 0.65, 0.33), (0.5, 1.6, 0.55), (-0.2, 2.9, 0.2)]:
yfit = m * xfit + b
plt.plot(xfit, yfit, '-k')
plt.fill_between(xfit, yfit - d, yfit + d, edgecolor='none',
color='#AAAAAA', alpha=0.4)
plt.xlim(-1, 3.5);
Из приведенного выше изображения в выходных данных мы легко можем наблюдать «поля» в рамках дискриминантных классификаторов. SVM выберет линию, которая максимизирует маржу.
Далее мы будем использовать классификатор векторов поддержки Scikit-Learn для обучения модели SVM на этих данных. Здесь мы используем линейное ядро для соответствия SVM следующим образом:
from sklearn.svm import SVC # "Support vector classifier"
model = SVC(kernel='linear', C=1E10)
model.fit(X, y)Результат выглядит следующим образом -
SVC(C=10000000000.0, cache_size=200, class_weight=None, coef0=0.0,
decision_function_shape='ovr', degree=3, gamma='auto_deprecated',
kernel='linear', max_iter=-1, probability=False, random_state=None,
shrinking=True, tol=0.001, verbose=False)Теперь, для лучшего понимания, ниже будут построены функции принятия решения для 2D SVC:
def decision_function(model, ax=None, plot_support=True):
if ax is None:
ax = plt.gca()
xlim = ax.get_xlim()
ylim = ax.get_ylim()Для оценки модели нам нужно создать сетку следующим образом:
x = np.linspace(xlim[0], xlim[1], 30)
y = np.linspace(ylim[0], ylim[1], 30)
Y, X = np.meshgrid(y, x)
xy = np.vstack([X.ravel(), Y.ravel()]).T
P = model.decision_function(xy).reshape(X.shape)Затем нам нужно построить границы решений и поля следующим образом:
ax.contour(X, Y, P, colors='k',
levels=[-1, 0, 1], alpha=0.5,
linestyles=['--', '-', '--'])Теперь аналогичным образом постройте опорные векторы следующим образом:
if plot_support:
ax.scatter(model.support_vectors_[:, 0],
model.support_vectors_[:, 1],
s=300, linewidth=1, facecolors='none');
ax.set_xlim(xlim)
ax.set_ylim(ylim)Теперь используйте эту функцию, чтобы соответствовать нашим моделям следующим образом:
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='summer')
decision_function(model);
Из вышеприведенных выходных данных мы можем наблюдать, что классификатор SVM соответствует данным с полями, то есть пунктирными линиями и опорными векторами, ключевыми элементами этого соответствия, касающимися пунктирной линии. Эти точки опорных векторов хранятся в атрибуте support_vectors_ классификатора следующим образом:
model.support_vectors_Результат выглядит следующим образом -
array([[0.5323772 , 3.31338909],
[2.11114739, 3.57660449],
[1.46870582, 1.86947425]])Ядра SVM
На практике алгоритм SVM реализуется с помощью ядра, которое преобразует пространство входных данных в требуемую форму. SVM использует технику, называемую трюком с ядром, в которой ядро берет низкоразмерное входное пространство и преобразует его в более высокомерное пространство. Проще говоря, ядро преобразует неразрывные проблемы в отдельные проблемы, добавляя к ним дополнительные измерения. Это делает SVM более мощным, гибким и точным. Ниже приведены некоторые из типов ядер, используемых SVM.
Линейное ядро
Его можно использовать как скалярное произведение между любыми двумя наблюдениями. Формула линейного ядра следующая:
k (x, x i ) = сумма (x * x i )
Из приведенной выше формулы мы видим, что произведение двух векторов говорит & - это сумма умножения каждой пары входных значений.
Полиномиальное ядро
Это более обобщенная форма линейного ядра, в которой различают искривленное или нелинейное входное пространство. Ниже приводится формула для полиномиального ядра -
K (x, xi) = 1 + сумма (x * xi) ^ d
Здесь d - степень полинома, которую нам нужно указать вручную в алгоритме обучения.
Ядро радиальной базисной функции (RBF)
Ядро RBF, в основном используемое в классификации SVM, отображает входное пространство в неопределенное пространство. Следующая формула объясняет это математически -
K (x, xi) = exp (-гамма * сумма ((x - xi ^ 2))
Здесь гамма варьируется от 0 до 1. Нам нужно вручную указать ее в алгоритме обучения. Хорошее значение гаммы по умолчанию - 0,1.
Поскольку мы реализовали SVM для линейно разделяемых данных, мы можем реализовать его на Python для данных, которые не являются линейно разделяемыми. Это можно сделать с помощью ядер.
пример
Ниже приведен пример создания классификатора SVM с использованием ядер. Мы будем использовать набор данных iris из scikit-learn -
Мы начнем с импорта следующих пакетов -
import pandas as pd
import numpy as np
from sklearn import svm, datasets
import matplotlib.pyplot as pltТеперь нам нужно загрузить входные данные -
iris = datasets.load_iris()Из этого набора данных мы берем первые две функции следующим образом:
X = iris.data[:, :2]
y = iris.targetЗатем мы построим границы SVM с исходными данными следующим образом:
x_min, x_max = X[:, 0].min() - 1, X[:, 0].max() + 1
y_min, y_max = X[:, 1].min() - 1, X[:, 1].max() + 1
h = (x_max / x_min)/100
xx, yy = np.meshgrid(np.arange(x_min, x_max, h),
np.arange(y_min, y_max, h))
X_plot = np.c_[xx.ravel(), yy.ravel()]Теперь нам нужно предоставить значение параметра регуляризации следующим образом:
C = 1.0Затем объект классификатора SVM может быть создан следующим образом:
Svc_classifier = svm.SVC (ядро = 'линейный', C = C) .fit (X, y)
Z = svc_classifier.predict(X_plot)
Z = Z.reshape(xx.shape)
plt.figure(figsize=(15, 5))
plt.subplot(121)
plt.contourf(xx, yy, Z, cmap=plt.cm.tab10, alpha=0.3)
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Set1)
plt.xlabel('Sepal length')
plt.ylabel('Sepal width')
plt.xlim(xx.min(), xx.max())
plt.title('Support Vector Classifier with linear kernel')Вывод
Text(0.5, 1.0, 'Support Vector Classifier with linear kernel')
Для создания классификатора SVM с rbf ядро, мы можем изменить ядро на rbf следующим образом -
Svc_classifier = svm.SVC(kernel='rbf', gamma =‘auto’,C=C).fit(X, y)
Z = svc_classifier.predict(X_plot)
Z = Z.reshape(xx.shape)
plt.figure(figsize=(15, 5))
plt.subplot(121)
plt.contourf(xx, yy, Z, cmap=plt.cm.tab10, alpha=0.3)
plt.scatter(X[:, 0], X[:, 1], c=y, cmap=plt.cm.Set1)
plt.xlabel('Sepal length')
plt.ylabel('Sepal width')
plt.xlim(xx.min(), xx.max())
plt.title('Support Vector Classifier with rbf kernel')Вывод
Text(0.5, 1.0, 'Support Vector Classifier with rbf kernel')
Мы устанавливаем значение гаммы на «авто», но вы также можете указать его значение от 0 до 1.
Плюсы и минусы классификаторов SVM
Плюсы SVM-классификаторов
Классификаторы SVM обеспечивают высокую точность и хорошо работают с пространством больших размеров. Классификаторы SVM в основном используют подмножество обучающих точек, поэтому в результате используется очень меньше памяти.
Минусы классификаторов SVM
У них много времени на обучение, поэтому на практике они не подходят для больших наборов данных. Другой недостаток заключается в том, что классификаторы SVM плохо работают с перекрывающимися классами.
Введение в дерево решений
В общем, анализ дерева решений - это инструмент прогнозного моделирования, который можно применять во многих областях. Деревья решений могут быть построены с помощью алгоритмического подхода, который может разбивать набор данных разными способами в зависимости от различных условий. Решения tress - это самые мощные алгоритмы, которые подпадают под категорию контролируемых алгоритмов.
Их можно использовать как для задач классификации, так и для регрессии. Две основные сущности дерева - это узлы принятия решений, где данные разделяются и уходят, где мы и получили результат. Пример двоичного дерева для прогнозирования того, подходит ли человек или нет, предоставляя различную информацию, такую как возраст, привычки питания и привычки упражнений, приведен ниже -
В приведенном выше дереве решений вопрос - это узлы решения, а окончательные результаты - это листья. У нас есть следующие два типа деревьев решений:
Classification decision trees- В этом виде деревьев решений переменная решения категориальна. Приведенное выше дерево решений является примером дерева решений по классификации.
Regression decision trees - В таких деревьях решений переменная решения является непрерывной.
Реализация алгоритма дерева решений
Индекс Джини
Это имя функции стоимости, которая используется для оценки двоичных разбиений в наборе данных и работает с категориальной целевой переменной «Успех» или «Неудача».
Чем выше значение индекса Джини, тем выше однородность. Идеальное значение индекса Джини равно 0, а худшее - 0,5 (для задачи 2 класса). Индекс Джини для сплита можно рассчитать с помощью следующих шагов -
Сначала рассчитайте индекс Джини для подузлов, используя формулу p ^ 2 + q ^ 2, которая представляет собой сумму квадрата вероятности успеха и неудачи.
Затем рассчитайте индекс Джини для разделения, используя взвешенный показатель Джини для каждого узла этого разделения.
Алгоритм дерева классификации и регрессии (CART) использует метод Джини для создания двоичных разбиений.
Разделить создание
Разделение в основном включает атрибут в наборе данных и значение. Мы можем создать разделение в наборе данных с помощью следующих трех частей:
Part1 - Расчет показателя Джини: мы только что обсудили эту часть в предыдущем разделе.
Part2- Разделение набора данных: это может быть определено как разделение набора данных на два списка строк, имеющих индекс атрибута и значение разделения этого атрибута. После получения двух групп - правой и левой из набора данных, мы можем вычислить значение разделения, используя показатель Джини, рассчитанный в первой части. Значение разделения будет определять, в какой группе будет находиться атрибут.
Part3- Оценка всех разбиений: следующая часть после нахождения показателя Джини и разбиения набора данных - это оценка всех разбиений. Для этого, во-первых, мы должны проверить каждое значение, связанное с каждым атрибутом, как возможное разбиение. Затем нам нужно найти наилучшее возможное разделение, оценив его стоимость. Лучшее разбиение будет использоваться в качестве узла в дереве решений.
Строим дерево
Как мы знаем, у дерева есть корневой узел и конечные узлы. После создания корневого узла мы можем построить дерево, выполнив две части:
Часть 1: Создание терминального узла
При создании конечных узлов дерева решений один важный момент - решить, когда прекратить рост дерева или создавать дополнительные конечные узлы. Это можно сделать, используя два критерия, а именно максимальную глубину дерева и минимальные записи узлов следующим образом:
Maximum Tree Depth- Как следует из названия, это максимальное количество узлов в дереве после корневого узла. Мы должны прекратить добавление конечных узлов, как только дерево достигнет максимальной глубины, т.е. когда дерево получит максимальное количество конечных узлов.
Minimum Node Records- Его можно определить как минимальное количество обучающих шаблонов, за которые отвечает данный узел. Мы должны прекратить добавление конечных узлов, как только дерево достигнет этого минимального количества записей узлов или ниже этого минимума.
Терминальный узел используется для окончательного прогноза.
Часть 2: Рекурсивное разделение
Когда мы поняли, когда создавать конечные узлы, теперь мы можем приступить к построению нашего дерева. Рекурсивное разбиение - это метод построения дерева. В этом методе после создания узла мы можем рекурсивно создавать дочерние узлы (узлы, добавленные к существующему узлу) для каждой группы данных, сгенерированных путем разделения набора данных, вызывая одну и ту же функцию снова и снова.
Предсказание
После построения дерева решений нам нужно сделать прогноз на этот счет. По сути, прогнозирование включает в себя навигацию по дереву решений с помощью специально предоставленной строки данных.
Мы можем сделать прогноз с помощью рекурсивной функции, как это было сделано выше. Та же самая процедура прогнозирования вызывается снова с левым или правым дочерним узлами.
Предположения
Ниже приведены некоторые предположения, которые мы делаем при создании дерева решений.
При подготовке деревьев решений обучающий набор является корневым узлом.
Классификатор дерева решений предпочитает, чтобы значения функций были категориальными. В случае, если вы хотите использовать непрерывные значения, они должны быть дискретизированы до построения модели.
На основе значений атрибутов записи распределяются рекурсивно.
Статистический подход будет использоваться для размещения атрибутов в любой позиции узла, то есть в качестве корневого узла или внутреннего узла.
Реализация на Python
пример
В следующем примере мы собираемся реализовать классификатор дерева решений для индейского диабета пима -
Сначала начнем с импорта необходимых пакетов Python -
import pandas as pd
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_splitЗатем загрузите набор данных iris по его веб-ссылке следующим образом:
col_names = ['pregnant', 'glucose', 'bp', 'skin', 'insulin', 'bmi', 'pedigree', 'age', 'label']
pima = pd.read_csv(r"C:\pima-indians-diabetes.csv", header=None, names=col_names)
pima.head()pregnant glucose bp skin insulin bmi pedigree age label
0 6 148 72 35 0 33.6 0.627 50 1
1 1 85 66 29 0 26.6 0.351 31 0
2 8 183 64 0 0 23.3 0.672 32 1
3 1 89 66 23 94 28.1 0.167 21 0
4 0 137 40 35 168 43.1 2.288 33 1Теперь разделите набор данных на функции и целевую переменную следующим образом:
feature_cols = ['pregnant', 'insulin', 'bmi', 'age','glucose','bp','pedigree']
X = pima[feature_cols] # Features
y = pima.label # Target variableДалее мы разделим данные на тренировочную и тестовую. Следующий код разделит набор данных на 70% данных обучения и 30% данных тестирования.
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=1)Затем обучите модель с помощью класса DecisionTreeClassifier из sklearn следующим образом:
clf = DecisionTreeClassifier()
clf = clf.fit(X_train,y_train)Наконец-то нам нужно сделать прогноз. Это можно сделать с помощью следующего скрипта -
y_pred = clf.predict(X_test)Затем мы можем получить оценку точности, матрицу путаницы и отчет о классификации следующим образом:
from sklearn.metrics import classification_report, confusion_matrix, accuracy_score
result = confusion_matrix(y_test, y_pred)
print("Confusion Matrix:")
print(result)
result1 = classification_report(y_test, y_pred)
print("Classification Report:",)
print (result1)
result2 = accuracy_score(y_test,y_pred)
print("Accuracy:",result2)Вывод
Confusion Matrix:
[[116 30]
[ 46 39]]
Classification Report:
precision recall f1-score support
0 0.72 0.79 0.75 146
1 0.57 0.46 0.51 85
micro avg 0.67 0.67 0.67 231
macro avg 0.64 0.63 0.63 231
weighted avg 0.66 0.67 0.66 231
Accuracy: 0.670995670995671Визуализация дерева решений
Приведенное выше дерево решений можно визуализировать с помощью следующего кода -
from sklearn.tree import export_graphviz
from sklearn.externals.six import StringIO
from IPython.display import Image
import pydotplus
dot_data = StringIO()
export_graphviz(clf, out_file=dot_data,
filled=True, rounded=True,
special_characters=True,feature_names = feature_cols,class_names=['0','1'])
graph = pydotplus.graph_from_dot_data(dot_data.getvalue())
graph.write_png('Pima_diabetes_Tree.png')
Image(graph.create_png())
Введение в наивный байесовский алгоритм
Наивные байесовские алгоритмы - это метод классификации, основанный на применении теоремы Байеса с сильным предположением, что все предикторы независимы друг от друга. Проще говоря, предполагается, что наличие функции в классе не зависит от наличия любой другой функции в том же классе. Например, телефон можно считать умным, если у него есть сенсорный экран, доступ в Интернет, хорошая камера и т. Д. Хотя все эти функции зависят друг от друга, они независимо влияют на вероятность того, что телефон является смартфоном.
В байесовской классификации основной интерес состоит в том, чтобы найти апостериорные вероятности, то есть вероятность метки с учетом некоторых наблюдаемых характеристик (|). С помощью теоремы Байеса мы можем выразить это в количественной форме следующим образом:
$P(L |features)= \frac{P(L)P(features |L)}{()}$Здесь (|) - апостериорная вероятность класса.
() - априорная вероятность класса.
(|) - это вероятность, которая представляет собой вероятность предиктора данного класса.
() - априорная вероятность предсказателя.
Построение модели с использованием наивного байеса в Python
Библиотека Python, Scikit learn - самая полезная библиотека, которая помогает нам построить наивную байесовскую модель на Python. У нас есть следующие три типа модели Наивного Байеса в библиотеке Scikit learn Python:
Гауссовский наивный байесовский
Это простейший наивный байесовский классификатор, предполагающий, что данные каждой метки взяты из простого распределения Гаусса.
Полиномиальный наивный байесовский
Другой полезный наивный байесовский классификатор - это полиномиальный наивный байесовский классификатор, в котором предполагается, что признаки взяты из простого полиномиального распределения. Такой наивный байесовский метод наиболее подходит для функций, представляющих дискретные подсчеты.
Бернулли Наив Байес
Другой важной моделью является Bernoulli Naïve Bayes, в которой предполагается, что функции являются двоичными (нули и единицы). Классификация текста с помощью модели «мешка слов» может быть применением наивного Байеса Бернулли.
пример
В зависимости от нашего набора данных мы можем выбрать любую из наивных байесовских моделей, описанных выше. Здесь мы реализуем гауссовскую наивную байесовскую модель в Python -
Мы начнем с необходимого импорта следующим образом -
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns; sns.set()Теперь, используя функцию make_blobs () Scikit learn, мы можем генерировать капли точек с гауссовым распределением следующим образом:
from sklearn.datasets import make_blobs
X, y = make_blobs(300, 2, centers=2, random_state=2, cluster_std=1.5)
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='summer');Затем для использования модели GaussianNB нам нужно импортировать и создать ее объект следующим образом:
from sklearn.naive_bayes import GaussianNB
model_GBN = GaussianNB()
model_GNB.fit(X, y);Теперь нам нужно сделать прогноз. Это можно сделать после создания некоторых новых данных следующим образом:
rng = np.random.RandomState(0)
Xnew = [-6, -14] + [14, 18] * rng.rand(2000, 2)
ynew = model_GNB.predict(Xnew)Затем мы рисуем новые данные, чтобы найти его границы -
plt.scatter(X[:, 0], X[:, 1], c=y, s=50, cmap='summer')
lim = plt.axis()
plt.scatter(Xnew[:, 0], Xnew[:, 1], c=ynew, s=20, cmap='summer', alpha=0.1)
plt.axis(lim);Теперь, с помощью следующей строки кодов, мы можем найти апостериорные вероятности первой и второй меток -
yprob = model_GNB.predict_proba(Xnew)
yprob[-10:].round(3)Вывод
array([[0.998, 0.002],
[1. , 0. ],
[0.987, 0.013],
[1. , 0. ],
[1. , 0. ],
[1. , 0. ],
[1. , 0. ],
[1. , 0. ],
[0. , 1. ],
[0.986, 0.014]])За и против
Плюсы
Ниже приведены некоторые плюсы использования наивных байесовских классификаторов.
Наивную байесовскую классификацию легко реализовать и быстро.
Он будет сходиться быстрее, чем дискриминационные модели, такие как логистическая регрессия.
Требуется меньше данных для обучения.
Они обладают высокой масштабируемостью по своей природе или линейно масштабируются в зависимости от количества предикторов и точек данных.
Он может делать вероятностные прогнозы и обрабатывать как непрерывные, так и дискретные данные.
Наивный байесовский алгоритм классификации может использоваться как для двоичных, так и для многоклассовых задач классификации.
Минусы
Ниже приведены некоторые минусы использования наивных байесовских классификаторов.
Одним из наиболее важных недостатков наивной байесовской классификации является ее сильная независимость от признаков, потому что в реальной жизни практически невозможно иметь набор признаков, полностью независимых друг от друга.
Другой проблемой наивной байесовской классификации является ее `` нулевая частота '', что означает, что если категориальная переменная имеет категорию, но не наблюдается в наборе обучающих данных, то наивная байесовская модель присвоит ей нулевую вероятность, и она не сможет сделать предсказание.
Применение наивной байесовской классификации
Ниже приведены некоторые распространенные применения наивной байесовской классификации:
Real-time prediction - Благодаря простоте реализации и быстроте вычислений его можно использовать для прогнозирования в реальном времени.
Multi-class prediction - Наивный алгоритм классификации Байеса может использоваться для прогнозирования апостериорной вероятности нескольких классов целевой переменной.
Text classification- Благодаря функции предсказания нескольких классов, алгоритмы наивной байесовской классификации хорошо подходят для классификации текста. Вот почему он также используется для решения таких задач, как фильтрация спама и анализ настроений.
Recommendation system - Наряду с такими алгоритмами, как совместная фильтрация, Naïve Bayes создает систему рекомендаций, которая может использоваться для фильтрации невидимой информации и прогнозирования погоды, которую пользователь захочет использовать в данном ресурсе или нет.
Введение
Случайный лес - это алгоритм обучения с учителем, который используется как для классификации, так и для регрессии. Но в основном он используется для задач классификации. Как мы знаем, лес состоит из деревьев, и чем больше деревьев, тем крепче лес. Точно так же алгоритм случайного леса создает деревья решений на выборках данных, затем получает прогноз от каждой из них и, наконец, выбирает лучшее решение посредством голосования. Это метод ансамбля, который лучше, чем отдельное дерево решений, потому что он уменьшает чрезмерную подгонку путем усреднения результата.
Работа алгоритма случайного леса
Мы можем понять работу алгоритма случайного леса с помощью следующих шагов:
Step1 - Во-первых, начните с выбора случайных выборок из заданного набора данных.
Step2- Затем этот алгоритм построит дерево решений для каждой выборки. Затем он получит результат прогноза из каждого дерева решений.
Step3 - На этом этапе голосование будет выполняться для каждого прогнозируемого результата.
Step4 - Наконец, выберите результат прогноза с наибольшим количеством голосов в качестве окончательного результата прогноза.
Следующая диаграмма проиллюстрирует его работу -

Реализация на Python
Сначала начнем с импорта необходимых пакетов Python -
import numpy as np
import matplotlib.pyplot as plt
import pandas as pdЗатем загрузите набор данных iris по его веб-ссылке следующим образом:
path = "https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data"Затем нам нужно назначить имена столбцов набору данных следующим образом:
headernames = ['sepal-length', 'sepal-width', 'petal-length', 'petal-width', 'Class']Теперь нам нужно прочитать набор данных в фреймворке pandas следующим образом:
dataset = pd.read_csv(path, names=headernames)
dataset.head()длина чашелистика |
ширина чашелистика |
длина лепестка |
ширина лепестка |
Класс |
|
|---|---|---|---|---|---|
0 |
5.1 |
3.5 |
1.4 |
0,2 |
Ирис-сетоса |
1 |
4.9 |
3.0 |
1.4 |
0,2 |
Ирис-сетоса |
2 |
4,7 |
3.2 |
1.3 |
0,2 |
Ирис-сетоса |
3 |
4.6 |
3.1 |
1.5 |
0,2 |
Ирис-сетоса |
4 |
5.0 |
3,6 |
1.4 |
0,2 |
Ирис-сетоса |
Предварительная обработка данных будет выполняться с помощью следующих строк скрипта -
X = dataset.iloc[:, :-1].values
y = dataset.iloc[:, 4].valuesДалее мы разделим данные на тренировочную и тестовую. Следующий код разделит набор данных на 70% данных обучения и 30% данных тестирования.
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.30)Затем обучите модель с помощью класса sklearn RandomForestClassifier следующим образом:
from sklearn.ensemble import RandomForestClassifier
classifier = RandomForestClassifier(n_estimators=50)
classifier.fit(X_train, y_train)Наконец, нам нужно сделать прогноз. Это можно сделать с помощью следующего скрипта -
y_pred = classifier.predict(X_test)Затем распечатайте результаты следующим образом -
from sklearn.metrics import classification_report, confusion_matrix, accuracy_score
result = confusion_matrix(y_test, y_pred)
print("Confusion Matrix:")
print(result)
result1 = classification_report(y_test, y_pred)
print("Classification Report:",)
print (result1)
result2 = accuracy_score(y_test,y_pred)
print("Accuracy:",result2)Вывод
Confusion Matrix:
[[14 0 0]
[ 0 18 1]
[ 0 0 12]]
Classification Report:
precision recall f1-score support
Iris-setosa 1.00 1.00 1.00 14
Iris-versicolor 1.00 0.95 0.97 19
Iris-virginica 0.92 1.00 0.96 12
micro avg 0.98 0.98 0.98 45
macro avg 0.97 0.98 0.98 45
weighted avg 0.98 0.98 0.98 45
Accuracy: 0.9777777777777777Плюсы и минусы случайного леса
Плюсы
Ниже приведены преимущества алгоритма случайного леса:
Он решает проблему переобучения за счет усреднения или объединения результатов различных деревьев решений.
Случайные леса лучше подходят для большого диапазона элементов данных, чем одно дерево решений.
Случайный лес имеет меньшую дисперсию, чем одно дерево решений.
Случайные леса очень гибкие и обладают очень высокой точностью.
В алгоритме случайного леса масштабирование данных не требуется. Он сохраняет хорошую точность даже после предоставления данных без масштабирования.
В алгоритме случайного леса масштабирование данных не требуется. Он сохраняет хорошую точность даже после предоставления данных без масштабирования.
Минусы
Ниже приведены недостатки алгоритма случайного леса:
Сложность - главный недостаток алгоритмов случайного леса.
Построение случайных лесов намного сложнее и требует много времени, чем деревья решений.
Для реализации алгоритма случайного леса требуется больше вычислительных ресурсов.
Это менее интуитивно понятно, если у нас большой набор деревьев решений.
Процесс прогнозирования с использованием случайных лесов занимает очень много времени по сравнению с другими алгоритмами.
Введение в регрессию
Регрессия - еще один важный и широко используемый инструмент статистического и машинного обучения. Ключевой целью задач на основе регрессии является прогнозирование выходных меток или ответов, которые являются продолжением числовых значений для заданных входных данных. Результат будет основан на том, что модель узнала на этапе обучения. По сути, регрессионные модели используют функции входных данных (независимые переменные) и соответствующие им непрерывные числовые выходные значения (зависимые или выходные переменные) для изучения конкретной связи между входами и соответствующими выходными данными.

Типы регрессионных моделей

Модели регрессии бывают следующих двух типов -
Simple regression model - Это самая простая регрессионная модель, в которой прогнозы формируются на основе одного одномерного признака данных.
Multiple regression model - Как следует из названия, в этой регрессионной модели прогнозы формируются на основе множества характеристик данных.
Создание регрессора в Python
Модель регрессора в Python можно построить так же, как мы построили классификатор. Scikit-learn, библиотека Python для машинного обучения также может использоваться для создания регрессора на Python.
В следующем примере мы будем строить базовую регрессионную модель, которая будет соответствовать строке данных, то есть линейному регрессору. Необходимые шаги для создания регрессора в Python следующие:
Шаг 1. Импорт необходимого пакета Python
Для создания регрессора с использованием scikit-learn нам необходимо импортировать его вместе с другими необходимыми пакетами. Мы можем импортировать, используя следующий скрипт -
import numpy as np
from sklearn import linear_model
import sklearn.metrics as sm
import matplotlib.pyplot as pltШаг 2. Импорт набора данных
После импорта необходимого пакета нам понадобится набор данных для построения модели прогнозирования регрессии. Мы можем импортировать его из набора данных sklearn или использовать другой в соответствии с нашими требованиями. Мы собираемся использовать наши сохраненные входные данные. Мы можем импортировать его с помощью следующего скрипта -
input = r'C:\linear.txt'Далее нам нужно загрузить эти данные. Мы используем функцию np.loadtxt для его загрузки.
input_data = np.loadtxt(input, delimiter=',')
X, y = input_data[:, :-1], input_data[:, -1]Шаг 3. Организация данных в наборы для обучения и тестирования
Поскольку нам нужно протестировать нашу модель на невидимых данных, мы разделим наш набор данных на две части: обучающий набор и тестовый набор. Следующая команда выполнит это -
training_samples = int(0.6 * len(X))
testing_samples = len(X) - num_training
X_train, y_train = X[:training_samples], y[:training_samples]
X_test, y_test = X[training_samples:], y[training_samples:]Шаг 4- Оценка и прогноз модели
После разделения данных на обучение и тестирование нам нужно построить модель. Для этой цели мы будем использовать функцию LineaRegression () Scikit-learn. Следующая команда создаст объект линейного регрессора.
reg_linear= linear_model.LinearRegression()Затем обучите эту модель с обучающими образцами следующим образом:
reg_linear.fit(X_train, y_train)Теперь, наконец, нам нужно сделать прогноз на основе данных тестирования.
y_test_pred = reg_linear.predict(X_test)Шаг 5- График и визуализация
После предсказания мы можем построить и визуализировать его с помощью следующего скрипта -
plt.scatter(X_test, y_test, color='red')
plt.plot(X_test, y_test_pred, color='black', linewidth=2)
plt.xticks(())
plt.yticks(())
plt.show()Вывод

В приведенном выше выводе мы видим линию регрессии между точками данных.
Step6- Performance computation - Мы также можем вычислить производительность нашей регрессионной модели с помощью различных показателей производительности следующим образом:
print("Regressor model performance:")
print("Mean absolute error(MAE) =", round(sm.mean_absolute_error(y_test, y_test_pred), 2))
print("Mean squared error(MSE) =", round(sm.mean_squared_error(y_test, y_test_pred), 2))
print("Median absolute error =", round(sm.median_absolute_error(y_test, y_test_pred), 2))
print("Explain variance score =", round(sm.explained_variance_score(y_test, y_test_pred), 2))
print("R2 score =", round(sm.r2_score(y_test, y_test_pred), 2))Вывод
Regressor model performance:
Mean absolute error(MAE) = 1.78
Mean squared error(MSE) = 3.89
Median absolute error = 2.01
Explain variance score = -0.09
R2 score = -0.09Типы алгоритмов регрессии машинного обучения
Самым полезным и популярным алгоритмом регрессии ML является алгоритм линейной регрессии, который далее делится на два типа, а именно:
Алгоритм простой линейной регрессии
Алгоритм множественной линейной регрессии.
Мы обсудим это и реализуем на Python в следующей главе.
Приложения
Применения алгоритмов регрессии ML следующие:
Forecasting or Predictive analysis- Одно из важных применений регрессии - это прогнозирование или прогнозный анализ. Например, мы можем прогнозировать ВВП, цены на нефть или, проще говоря, количественные данные, которые меняются с течением времени.
Optimization- Мы можем оптимизировать бизнес-процессы с помощью регрессии. Например, менеджер магазина может создать статистическую модель, чтобы понять, когда приходят клиенты.
Error correction- В бизнесе принятие правильного решения не менее важно, чем оптимизация бизнес-процесса. Регрессия может помочь нам принять правильное решение, а также исправить уже реализованное решение.
Economics- Это наиболее часто используемый инструмент в экономике. Мы можем использовать регрессию для прогнозирования предложения, спроса, потребления, инвестиций в запасы и т. Д.
Finance- Финансовая компания всегда заинтересована в минимизации портфеля рисков и хочет знать факторы, которые влияют на клиентов. Все это можно предсказать с помощью регрессионной модели.
Введение в линейную регрессию
Линейная регрессия может быть определена как статистическая модель, которая анализирует линейную связь между зависимой переменной с заданным набором независимых переменных. Линейная связь между переменными означает, что, когда значение одной или нескольких независимых переменных изменится (увеличится или уменьшится), значение зависимой переменной также изменится соответственно (увеличится или уменьшится).
Математически связь может быть представлена с помощью следующего уравнения -
Y = mX + b
Здесь Y - зависимая переменная, которую мы пытаемся предсказать.
X - зависимая переменная, которую мы используем, чтобы делать прогнозы.
m - наклон линии регрессии, которая представляет влияние X на Y
b - константа, известная как Y-пересечение. Если X = 0, Y будет равно b.
Кроме того, линейная зависимость может быть положительной или отрицательной по своей природе, как описано ниже -
Положительная линейная связь
Линейная зависимость будет называться положительной, если увеличивается как независимая, так и зависимая переменная. Это можно понять с помощью следующего графика -

Отрицательная линейная связь
Линейная зависимость будет называться положительной, если независимая увеличивается, а зависимая переменная уменьшается. Это можно понять с помощью следующего графика -

Типы линейной регрессии
Линейная регрессия бывает следующих двух типов -
Простая линейная регрессия
Множественная линейная регрессия
Простая линейная регрессия (SLR)
Это самая простая версия линейной регрессии, которая предсказывает ответ с помощью одной функции. В SLR предполагается, что две переменные линейно связаны.
Реализация Python
Мы можем реализовать SLR в Python двумя способами: один - предоставить собственный набор данных, а другой - использовать набор данных из библиотеки python scikit-learn.
Example1 - В следующем примере реализации Python мы используем наш собственный набор данных.
Во-первых, мы начнем с импорта необходимых пакетов следующим образом:
%matplotlib inline
import numpy as np
import matplotlib.pyplot as pltЗатем определите функцию, которая будет вычислять важные значения для SLR -
def coef_estimation(x, y):Следующая строка скрипта даст количество наблюдений n -
n = np.size(x)Среднее значение вектора x и y можно рассчитать следующим образом:
m_x, m_y = np.mean(x), np.mean(y)Мы можем найти перекрестное отклонение и отклонение относительно x следующим образом:
SS_xy = np.sum(y*x) - n*m_y*m_x
SS_xx = np.sum(x*x) - n*m_x*m_xЗатем коэффициенты регрессии, т.е. b, можно рассчитать следующим образом:
b_1 = SS_xy / SS_xx
b_0 = m_y - b_1*m_x
return(b_0, b_1)Затем нам нужно определить функцию, которая будет строить линию регрессии, а также предсказывать вектор ответа -
def plot_regression_line(x, y, b):Следующая строка сценария отобразит фактические точки как диаграмму рассеяния -
plt.scatter(x, y, color = "m", marker = "o", s = 30)Следующая строка сценария предсказывает вектор ответа -
y_pred = b[0] + b[1]*xСледующие строки скрипта построят линию регрессии и поместят на них метки:
plt.plot(x, y_pred, color = "g")
plt.xlabel('x')
plt.ylabel('y')
plt.show()Наконец, нам нужно определить функцию main () для предоставления набора данных и вызова функции, которую мы определили выше -
def main():
x = np.array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
y = np.array([100, 300, 350, 500, 750, 800, 850, 900, 1050, 1250])
b = coef_estimation(x, y)
print("Estimated coefficients:\nb_0 = {} \nb_1 = {}".format(b[0], b[1]))
plot_regression_line(x, y, b)
if __name__ == "__main__":
main()Вывод
Estimated coefficients:
b_0 = 154.5454545454545
b_1 = 117.87878787878788
Example2 - В следующем примере реализации Python мы используем набор данных о диабете из scikit-learn.
Во-первых, мы начнем с импорта необходимых пакетов следующим образом:
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, linear_model
from sklearn.metrics import mean_squared_error, r2_scoreЗатем мы загрузим набор данных о диабете и создадим его объект -
diabetes = datasets.load_diabetes()Поскольку мы внедряем SLR, мы будем использовать только одну функцию, а именно:
X = diabetes.data[:, np.newaxis, 2]Затем нам нужно разделить данные на наборы для обучения и тестирования следующим образом:
X_train = X[:-30]
X_test = X[-30:]Затем нам нужно разделить цель на обучающий и тестовый наборы следующим образом:
y_train = diabetes.target[:-30]
y_test = diabetes.target[-30:]Теперь, чтобы обучить модель, нам нужно создать объект линейной регрессии следующим образом:
regr = linear_model.LinearRegression()Затем обучите модель с помощью обучающих наборов следующим образом:
regr.fit(X_train, y_train)Затем сделайте прогнозы, используя набор для тестирования следующим образом:
y_pred = regr.predict(X_test)Затем мы напечатаем некоторые коэффициенты, такие как MSE, оценка дисперсии и т. Д., Следующим образом:
print('Coefficients: \n', regr.coef_)
print("Mean squared error: %.2f"
% mean_squared_error(y_test, y_pred))
print('Variance score: %.2f' % r2_score(y_test, y_pred))Теперь постройте выходные данные следующим образом -
plt.scatter(X_test, y_test, color='blue')
plt.plot(X_test, y_pred, color='red', linewidth=3)
plt.xticks(())
plt.yticks(())
plt.show()Вывод
Coefficients:
[941.43097333]
Mean squared error: 3035.06
Variance score: 0.41
Множественная линейная регрессия (MLR)
Это расширение простой линейной регрессии, которая предсказывает ответ с использованием двух или более функций. Математически мы можем объяснить это следующим образом:
Рассмотрим набор данных, содержащий n наблюдений, p функций, то есть независимых переменных, и y как один ответ, то есть зависимую переменную, линия регрессии для p функций может быть рассчитана следующим образом:
$h(x_{i})=b_{0}+b_{1}x_{i1}+b_{2}x_{i2}+...+b_{p}x_{ip}$Здесь h (x i ) - это прогнозируемое значение отклика, а b 0 , b 1 , b 2… , b p - коэффициенты регрессии.
Модели множественной линейной регрессии всегда включают ошибки в данных, известные как остаточная ошибка, которая изменяет расчет следующим образом:
$h(x_{i})=b_{0}+b_{1}x_{i1}+b_{2}x_{i2}+...+b_{p}x_{ip}+e_{i}$Мы также можем записать приведенное выше уравнение следующим образом -
$y_{i}=h(x_{i})+e_{i}$ $e_{i}= y_{i} - h(x_{i})$Реализация Python
в этом примере мы будем использовать набор данных о жилье Бостона из scikit learn -
Во-первых, мы начнем с импорта необходимых пакетов следующим образом:
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
from sklearn import datasets, linear_model, metricsЗатем загрузите набор данных следующим образом -
boston = datasets.load_boston(return_X_y=False)Следующие строки скрипта будут определять матрицу признаков X и вектор ответа Y -
X = boston.data
y = boston.targetЗатем разделите набор данных на наборы для обучения и тестирования следующим образом:
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.7, random_state=1)Теперь создайте объект линейной регрессии и обучите модель следующим образом:
reg = linear_model.LinearRegression()
reg.fit(X_train, y_train)
print('Coefficients: \n', reg.coef_)
print('Variance score: {}'.format(reg.score(X_test, y_test)))
plt.style.use('fivethirtyeight')
plt.scatter(reg.predict(X_train), reg.predict(X_train) - y_train,
color = "green", s = 10, label = 'Train data')
plt.scatter(reg.predict(X_test), reg.predict(X_test) - y_test,
color = "blue", s = 10, label = 'Test data')
plt.hlines(y = 0, xmin = 0, xmax = 50, linewidth = 2)
plt.legend(loc = 'upper right')
plt.title("Residual errors")
plt.show()Вывод
Coefficients:
[-1.16358797e-01 6.44549228e-02 1.65416147e-01 1.45101654e+00
-1.77862563e+01 2.80392779e+00 4.61905315e-02 -1.13518865e+00
3.31725870e-01 -1.01196059e-02 -9.94812678e-01 9.18522056e-03
-7.92395217e-01]
Variance score: 0.709454060230326
Предположения
Ниже приведены некоторые предположения о наборе данных, который сделан моделью линейной регрессии.
Multi-collinearity- Модель линейной регрессии предполагает, что в данных очень мало или совсем нет мультиколлинеарности. По сути, мультиколлинеарность возникает, когда независимые переменные или функции имеют в них зависимости.
Auto-correlation- Другое предположение, которое предполагает модель линейной регрессии, состоит в том, что в данных очень мало автокорреляции или она отсутствует. Как правило, автокорреляция возникает, когда существует зависимость между остаточными ошибками.
Relationship between variables - Модель линейной регрессии предполагает, что связь между откликом и характеристическими переменными должна быть линейной.
Введение в кластеризацию
Методы кластеризации - один из самых полезных методов машинного обучения без учителя. Эти методы используются для поиска сходства, а также закономерностей отношений между выборками данных, а затем группируют эти образцы в группы, имеющие сходство на основе характеристик.
Кластеризация важна, потому что она определяет внутреннюю группировку среди имеющихся немаркированных данных. Они в основном делают некоторые предположения о точках данных, чтобы определить их сходство. Каждое предположение будет создавать разные, но одинаково достоверные кластеры.
Например, ниже приведена диаграмма, на которой показана система кластеризации, сгруппированная вместе схожими типами данных в разных кластерах:

Методы формирования кластеров
Необязательно, чтобы кластеры образовывали сферическую форму. Ниже приведены некоторые другие методы формирования кластеров -
На основе плотности
В этих методах кластеры формируются в виде плотной области. Преимущество этих методов в том, что они обладают хорошей точностью, а также хорошей способностью объединить два кластера. Ex. Пространственная кластеризация приложений с шумом на основе плотности (DBSCAN), точки упорядочивания для определения структуры кластеризации (OPTICS) и т. Д.
На основе иерархии
В этих методах кластеры формируются в виде древовидной структуры на основе иерархии. У них есть две категории, а именно: агломеративные (подход снизу вверх) и разделительные (подход сверху вниз). Ex. Кластеризация с использованием представителей (CURE), сбалансированная итеративная сокращающая кластеризация с использованием иерархий (BIRCH) и т. Д.
Разбиение
В этих методах кластеры формируются путем разделения объектов на k кластеров. Количество кластеров будет равно количеству разделов. Ex. K-means, кластеризация больших приложений на основе рандомизированного поиска (CLARANS).
Сетка
В этих методах кластеры формируются в виде сетчатой структуры. Преимущество этих методов заключается в том, что все операции кластеризации, выполняемые в этих сетках, выполняются быстро и не зависят от количества объектов данных. Ex. Сетка статистической информации (STING), Кластеризация в Quest (CLIQUE).
Измерение эффективности кластеризации
Одно из наиболее важных соображений относительно модели машинного обучения - оценка ее производительности или, можно сказать, качества модели. В случае алгоритмов обучения с учителем оценить качество нашей модели легко, потому что у нас уже есть метки для каждого примера.
С другой стороны, в случае алгоритмов неконтролируемого обучения нам не очень повезло, потому что мы имеем дело с немаркированными данными. Но все же у нас есть некоторые метрики, которые дают практикующему представление о том, что происходит изменение в кластерах в зависимости от алгоритма.
Прежде чем мы углубимся в такие метрики, мы должны понять, что эти метрики только оценивают сравнительную производительность моделей по отношению друг к другу, а не измеряют достоверность прогноза модели. Ниже приведены некоторые из показателей, которые мы можем развернуть в алгоритмах кластеризации для измерения качества модели.
Анализ силуэта
Силуэтный анализ, используемый для проверки качества модели кластеризации путем измерения расстояния между кластерами. По сути, это дает нам возможность оценить такие параметры, как количество кластеров, с помощьюSilhouette score. Эта оценка измеряет, насколько близко каждая точка в одном кластере находится к точкам в соседних кластерах.
Анализ оценки силуэта
Диапазон оценки Silhouette составляет [-1, 1]. Его анализ выглядит следующим образом -
+1 Score - Рядом +1 Silhouette score указывает на то, что образец находится далеко от соседнего кластера.
0 Score - 0 Silhouette score указывает, что образец находится на границе принятия решения, разделяющей два соседних кластера, или очень близко к ней.
-1 Score & минус -1 Silhouette score указывает, что образцы были назначены неправильным кластерам.
Расчет очков Silhouette можно выполнить по следующей формуле -
= (-) / (,)
Здесь = среднее расстояние до точек в ближайшем кластере
И = среднее внутрикластерное расстояние до всех точек.
Индекс Дэвиса-Болдина
Индекс БД - еще один хороший показатель для анализа алгоритмов кластеризации. С помощью индекса БД мы можем понять следующие моменты модели кластеризации:
Удачно ли расположены кластеры друг от друга или нет?
Насколько плотны кластеры?
Мы можем рассчитать индекс БД с помощью следующей формулы -
$DB=\frac{1}{n}\displaystyle\sum\limits_{i=1}^n max_{j\neq{i}}\left(\frac{\sigma_{i}+\sigma_{j}}{d(c_{i},c_{j})}\right)$Здесь = количество кластеров
σ i = среднее расстояние всех точек в кластере от центра тяжести кластера.
Чем меньше индекс БД, тем лучше модель кластеризации.
Индекс Данна
Он работает так же, как индекс БД, но есть следующие моменты, в которых оба отличаются:
Индекс Данна учитывает только наихудший случай, т.е. кластеры, которые расположены близко друг к другу, в то время как индекс DB учитывает дисперсию и разделение всех кластеров в модели кластеризации.
Индекс Данна увеличивается по мере увеличения производительности, в то время как индекс БД становится лучше, когда кластеры хорошо разнесены и плотны.
Мы можем рассчитать индекс Данна с помощью следующей формулы -
$D=\frac{min_{1\leq i <{j}\leq{n}}P(i,j)}{mix_{1\leq i < k \leq n}q(k)}$Здесь ,, = каждый индекс для кластеров
= межкластерное расстояние
q = расстояние внутри кластера
Типы алгоритмов кластеризации машинного обучения
Ниже приведены наиболее важные и полезные алгоритмы кластеризации машинного обучения.
К-означает кластеризацию
Этот алгоритм кластеризации вычисляет центроиды и выполняет итерацию, пока не найдет оптимальный центроид. Предполагается, что количество кластеров уже известно. Его также называют алгоритмом плоской кластеризации. Количество кластеров, идентифицированных алгоритмом из данных, обозначено буквой K в K-средних.
Алгоритм среднего сдвига
Это еще один мощный алгоритм кластеризации, используемый при обучении без учителя. В отличие от кластеризации K-средних, он не делает никаких предположений, следовательно, это непараметрический алгоритм.
Иерархическая кластеризация
Это еще один алгоритм обучения без учителя, который используется для группировки немаркированных точек данных, имеющих схожие характеристики.
Мы подробно обсудим все эти алгоритмы в следующих главах.
Приложения кластеризации
Мы можем найти кластеризацию полезной в следующих областях:
Data summarization and compression- Кластеризация широко используется в тех областях, где нам также требуется суммирование, сжатие и сокращение данных. Примеры - обработка изображений и векторное квантование.
Collaborative systems and customer segmentation - Поскольку кластеризацию можно использовать для поиска похожих продуктов или пользователей того же типа, ее можно использовать в области систем для совместной работы и сегментации клиентов.
Serve as a key intermediate step for other data mining tasks- Кластерный анализ может генерировать компактную сводку данных для классификации, тестирования, генерации гипотез; следовательно, он также служит ключевым промежуточным этапом для других задач интеллектуального анализа данных.
Trend detection in dynamic data - Кластеризация также может использоваться для обнаружения тенденций в динамических данных путем создания различных кластеров схожих тенденций.
Social network analysis- Кластеризация может использоваться при анализе социальных сетей. Примеры - создание последовательностей в изображениях, видео или аудио.
Biological data analysis - Кластеризация также может использоваться для создания кластеров изображений, видео, поэтому ее можно успешно использовать в анализе биологических данных.
Введение в алгоритм K-средних
Алгоритм кластеризации K-средних вычисляет центроиды и выполняет итерацию, пока не найдет оптимальный центроид. Предполагается, что количество кластеров уже известно. Его еще называютflat clusteringалгоритм. Количество кластеров, идентифицированных алгоритмом из данных, обозначено буквой K в K-средних.
В этом алгоритме точки данных назначаются кластеру таким образом, чтобы сумма квадрата расстояния между точками данных и центроидом была минимальной. Следует понимать, что меньшие вариации внутри кластеров приведут к большему количеству похожих точек данных в одном и том же кластере.
Работа алгоритма K-средних
Мы можем понять работу алгоритма кластеризации K-Means с помощью следующих шагов:
Step1 - Во-первых, нам нужно указать количество кластеров K, которые должны быть сгенерированы этим алгоритмом.
Step2- Затем случайным образом выберите K точек данных и назначьте каждую точку данных кластеру. Проще говоря, классифицируйте данные по количеству точек данных.
Step3 - Теперь он будет вычислять центроиды кластера.
Step4 - Затем продолжайте повторять следующее, пока мы не найдем оптимальный центроид, который представляет собой назначение точек данных кластерам, которые больше не меняются -
4.1 - Сначала будет вычислена сумма квадратов расстояния между точками данных и центроидами.
4.2 - Теперь мы должны назначить каждую точку данных кластеру, который находится ближе, чем другой кластер (центроид).
4.3 - Наконец, вычислите центроиды для кластеров, взяв среднее значение всех точек данных этого кластера.
K-означает следующее Expectation-Maximizationподход к решению проблемы. Шаг ожидания используется для присвоения точек данных ближайшему кластеру, а шаг максимизации используется для вычисления центроида каждого кластера.
При работе с алгоритмом K-средних нам необходимо позаботиться о следующих вещах:
При работе с алгоритмами кластеризации, включая K-средние, рекомендуется стандартизировать данные, поскольку такие алгоритмы используют измерение на основе расстояния для определения сходства между точками данных.
Из-за итеративного характера K-средних и случайной инициализации центроидов, K-средние могут придерживаться локального оптимума и могут не сходиться к глобальному оптимуму. Поэтому рекомендуется использовать разные инициализации центроидов.
Реализация на Python
Следующие два примера реализации алгоритма кластеризации K-средних помогут нам лучше понять его:
Пример1
Это простой пример, чтобы понять, как работают k-means. В этом примере мы сначала сгенерируем 2D-набор данных, содержащий 4 разных капли, а затем применим алгоритм k-средних, чтобы увидеть результат.
Сначала мы начнем с импорта необходимых пакетов -
%matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sns; sns.set()
import numpy as np
from sklearn.cluster import KMeansСледующий код сгенерирует 2D, содержащий четыре капли -
from sklearn.datasets.samples_generator import make_blobs
X, y_true = make_blobs(n_samples=400, centers=4, cluster_std=0.60, random_state=0)Затем следующий код поможет нам визуализировать набор данных -
plt.scatter(X[:, 0], X[:, 1], s=20);
plt.show()
Затем создайте объект KMeans вместе с указанием количества кластеров, обучите модель и выполните прогноз следующим образом:
kmeans = KMeans(n_clusters=4)
kmeans.fit(X)
y_kmeans = kmeans.predict(X)Теперь с помощью следующего кода мы можем построить и визуализировать центры кластера, выбранные оценщиком Python k-means:
plt.scatter(X[:, 0], X[:, 1], c=y_kmeans, s=20, cmap='summer')
centers = kmeans.cluster_centers_
plt.scatter(centers[:, 0], centers[:, 1], c='blue', s=100, alpha=0.9);
plt.show()
Пример 2
Давайте перейдем к другому примеру, в котором мы собираемся применить кластеризацию K-средних к набору данных простых цифр. K-means попытается определить похожие цифры без использования исходной информации на этикетке.
Сначала мы начнем с импорта необходимых пакетов -
%matplotlib inline
import matplotlib.pyplot as plt
import seaborn as sns; sns.set()
import numpy as np
from sklearn.cluster import KMeansЗатем загрузите набор данных цифр из sklearn и сделайте из него объект. Мы также можем найти количество строк и столбцов в этом наборе данных следующим образом:
from sklearn.datasets import load_digits
digits = load_digits()
digits.data.shapeВывод
(1797, 64)Приведенный выше вывод показывает, что этот набор данных содержит 1797 образцов с 64 функциями.
Мы можем выполнить кластеризацию, как в примере 1 выше -
kmeans = KMeans(n_clusters=10, random_state=0)
clusters = kmeans.fit_predict(digits.data)
kmeans.cluster_centers_.shapeВывод
(10, 64)Приведенный выше вывод показывает, что K-means создал 10 кластеров с 64 функциями.
fig, ax = plt.subplots(2, 5, figsize=(8, 3))
centers = kmeans.cluster_centers_.reshape(10, 8, 8)
for axi, center in zip(ax.flat, centers):
axi.set(xticks=[], yticks=[])
axi.imshow(center, interpolation='nearest', cmap=plt.cm.binary)Вывод
На выходе мы получим следующее изображение, на котором показаны центры кластеров, полученные с помощью k-средних.

Следующие строки кода будут сопоставлять изученные метки кластера с найденными в них истинными метками:
from scipy.stats import mode
labels = np.zeros_like(clusters)
for i in range(10):
mask = (clusters == i)
labels[mask] = mode(digits.target[mask])[0]Затем мы можем проверить точность следующим образом -
from sklearn.metrics import accuracy_score
accuracy_score(digits.target, labels)Вывод
0.7935447968836951Приведенный выше вывод показывает, что точность составляет около 80%.
Преимущества и недостатки
Преимущества
Ниже приведены некоторые преимущества алгоритмов кластеризации K-средних:
Это очень легко понять и реализовать.
Если у нас есть большое количество переменных, то K-средних будет быстрее, чем иерархическая кластеризация.
При повторном вычислении центроидов экземпляр может изменить кластер.
Более плотные кластеры формируются с помощью K-средних по сравнению с иерархической кластеризацией.
Недостатки
Ниже приведены некоторые недостатки алгоритмов кластеризации K-средних:
Сложно предсказать количество кластеров, то есть значение k.
На выход сильно влияют исходные данные, такие как количество кластеров (значение k).
Порядок данных будет иметь сильное влияние на конечный результат.
Он очень чувствителен к изменению масштаба. Если мы изменим масштаб наших данных с помощью нормализации или стандартизации, то вывод полностью изменится. Конечный вывод.
Если кластеры имеют сложную геометрическую форму, это нехорошо.
Применение алгоритма кластеризации K-средних
Основные цели кластерного анализа:
Чтобы получить осмысленную интуицию на основе данных, с которыми мы работаем.
Кластер, затем спрогнозируйте, где будут построены разные модели для разных подгрупп.
Для достижения вышеупомянутых целей кластеризация K-средних работает достаточно хорошо. Его можно использовать в следующих приложениях -
Сегментация рынка
Кластеризация документов
Сегментация изображения
Сжатие изображения
Сегментация клиентов
Анализ тренда на динамических данных
Введение в алгоритм среднего сдвига
Как обсуждалось ранее, это еще один мощный алгоритм кластеризации, используемый при обучении без учителя. В отличие от кластеризации K-средних, она не делает никаких предположений; следовательно, это непараметрический алгоритм.
Алгоритм среднего сдвига в основном назначает точки данных кластерам итеративно, смещая точки в сторону максимальной плотности точек данных, то есть центроида кластера.
Разница между алгоритмом K-Means и Mean-Shift заключается в том, что позже не нужно указывать количество кластеров заранее, потому что количество кластеров будет определяться алгоритмом по данным.
Работа алгоритма среднего сдвига
Мы можем понять работу алгоритма кластеризации среднего сдвига с помощью следующих шагов:
Step1 - Во-первых, начните с точек данных, назначенных собственному кластеру.
Step2 - Затем этот алгоритм вычислит центроиды.
Step3 - На этом шаге будет обновлено расположение новых центроидов.
Step4 - Теперь процесс будет повторен и перемещен в область более высокой плотности.
Step5 - Наконец, он будет остановлен, как только центроиды достигнут позиции, откуда он не может двигаться дальше.
Реализация на Python
Это простой пример, чтобы понять, как работает алгоритм Mean-Shift. В этом примере мы сначала сгенерируем 2D-набор данных, содержащий 4 разных капли, а затем применим алгоритм Mean-Shift, чтобы увидеть результат.
%matplotlib inline
import numpy as np
from sklearn.cluster import MeanShift
import matplotlib.pyplot as plt
from matplotlib import style
style.use("ggplot")
from sklearn.datasets.samples_generator import make_blobs
centers = [[3,3,3],[4,5,5],[3,10,10]]
X, _ = make_blobs(n_samples = 700, centers = centers, cluster_std = 0.5)
plt.scatter(X[:,0],X[:,1])
plt.show()
ms = MeanShift()
ms.fit(X)
labels = ms.labels_
cluster_centers = ms.cluster_centers_
print(cluster_centers)
n_clusters_ = len(np.unique(labels))
print("Estimated clusters:", n_clusters_)
colors = 10*['r.','g.','b.','c.','k.','y.','m.']
for i in range(len(X)):
plt.plot(X[i][0], X[i][1], colors[labels[i]], markersize = 3)
plt.scatter(cluster_centers[:,0],cluster_centers[:,1],
marker=".",color='k', s=20, linewidths = 5, zorder=10)
plt.show()Вывод
[[ 2.98462798 9.9733794 10.02629344]
[ 3.94758484 4.99122771 4.99349433]
[ 3.00788996 3.03851268 2.99183033]]
Estimated clusters: 3
Преимущества и недостатки
Преимущества
Ниже приведены некоторые преимущества алгоритма кластеризации среднего сдвига.
Нет необходимости делать какие-либо модельные предположения, как в случае K-средних или гауссовой смеси.
Он также может моделировать сложные кластеры невыпуклой формы.
Ему нужен только один параметр с именем bandwidth, который автоматически определяет количество кластеров.
Нет такой проблемы с локальными минимумами, как в K-средних.
Никаких проблем не возникает из-за выбросов.
Недостатки
Ниже приведены некоторые недостатки алгоритма кластеризации среднего сдвига.
Алгоритм среднего сдвига плохо работает в случае большой размерности, когда количество кластеров резко меняется.
У нас нет прямого контроля над количеством кластеров, но в некоторых приложениях нам нужно определенное количество кластеров.
Он не может различать значимые и бессмысленные режимы.
Введение в иерархическую кластеризацию
Иерархическая кластеризация - еще один алгоритм обучения без учителя, который используется для группировки немаркированных точек данных, имеющих схожие характеристики. Алгоритмы иерархической кластеризации делятся на следующие две категории:
Agglomerative hierarchical algorithms- В агломеративных иерархических алгоритмах каждая точка данных обрабатывается как единый кластер, а затем последовательно объединяются или агломерируются (восходящий подход) пары кластеров. Иерархия кластеров представлена в виде дендрограммы или древовидной структуры.
Divisive hierarchical algorithms - С другой стороны, в разделяющих иерархических алгоритмах все точки данных обрабатываются как один большой кластер, а процесс кластеризации включает разделение (подход сверху-вниз) одного большого кластера на несколько небольших кластеров.
Шаги по выполнению агломеративной иерархической кластеризации
Мы собираемся объяснить наиболее используемую и важную иерархическую кластеризацию, то есть агломеративную. Шаги, чтобы выполнить то же самое, следующие:
Step1- Рассматривайте каждую точку данных как один кластер. Следовательно, в начале у нас будет, скажем, K кластеров. Количество точек данных также будет K в начале.
Step2- Теперь на этом шаге нам нужно сформировать большой кластер, объединив две точки данных в шкафу. В результате получатся кластеры K-1.
Step3- Теперь, чтобы сформировать больше кластеров, нам нужно объединить два кластера туалетов. В результате получатся кластеры K-2.
Step4 - Теперь, чтобы сформировать один большой кластер, повторите три вышеуказанных шага до тех пор, пока K не станет равным 0, т. Е. Больше не останется точек данных для объединения.
Step5 - Наконец, после создания одного большого кластера дендрограммы будут использоваться для разделения на несколько кластеров в зависимости от проблемы.
Роль дендрограмм в агломеративной иерархической кластеризации
Как мы обсуждали на последнем шаге, роль дендрограммы начинается после формирования большого кластера. Дендрограмма будет использоваться для разделения кластеров на несколько кластеров связанных точек данных в зависимости от нашей проблемы. Это можно понять с помощью следующего примера -
Пример1
Чтобы понять, давайте начнем с импорта необходимых библиотек следующим образом:
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as npДалее мы будем рисовать точки данных, которые мы взяли для этого примера -
X = np.array([[7,8],[12,20],[17,19],[26,15],[32,37],[87,75],[73,85], [62,80],[73,60],[87,96],])
labels = range(1, 11)
plt.figure(figsize=(10, 7))
plt.subplots_adjust(bottom=0.1)
plt.scatter(X[:,0],X[:,1], label='True Position')
for label, x, y in zip(labels, X[:, 0], X[:, 1]):
plt.annotate(label,xy=(x, y), xytext=(-3, 3),textcoords='offset points', ha='right', va='bottom')
plt.show()
Из приведенной выше диаграммы очень легко увидеть, что у нас есть два кластера в наших точках данных, но в реальных данных могут быть тысячи кластеров. Далее мы будем строить дендрограммы наших точек данных с помощью библиотеки Scipy -
from scipy.cluster.hierarchy import dendrogram, linkage
from matplotlib import pyplot as plt
linked = linkage(X, 'single')
labelList = range(1, 11)
plt.figure(figsize=(10, 7))
dendrogram(linked, orientation='top',labels=labelList, distance_sort='descending',show_leaf_counts=True)
plt.show()
Теперь, когда сформирован большой кластер, выбирается самое длинное расстояние по вертикали. Затем через него проводится вертикальная линия, как показано на следующей диаграмме. Поскольку горизонтальная линия пересекает синюю линию в двух точках, количество кластеров будет равно двум.

Затем нам нужно импортировать класс для кластеризации и вызвать его метод fit_predict для прогнозирования кластера. Мы импортируем класс AgglomerativeClustering из библиотеки sklearn.cluster -
from sklearn.cluster import AgglomerativeClustering
cluster = AgglomerativeClustering(n_clusters=2, affinity='euclidean', linkage='ward')
cluster.fit_predict(X)Затем постройте кластер с помощью следующего кода -
plt.scatter(X[:,0],X[:,1], c=cluster.labels_, cmap='rainbow')
На приведенной выше диаграмме показаны два кластера из наших точек данных.
Пример2
Поскольку мы поняли концепцию дендрограмм из простого примера, рассмотренного выше, давайте перейдем к другому примеру, в котором мы создаем кластеры точки данных в наборе данных о диабете Pima Indian Diabetes Dataset, используя иерархическую кластеризацию -
import matplotlib.pyplot as plt
import pandas as pd
%matplotlib inline
import numpy as np
from pandas import read_csv
path = r"C:\pima-indians-diabetes.csv"
headernames = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=headernames)
array = data.values
X = array[:,0:8]
Y = array[:,8]
data.shape
(768, 9)
data.head()| слно. | preg | Plas | Pres | кожа | контрольная работа | масса | педи | возраст | класс |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 6 | 148 | 72 | 35 год | 0 | 33,6 | 0,627 | 50 | 1 |
| 1 | 1 | 85 | 66 | 29 | 0 | 26,6 | 0,351 | 31 год | 0 |
| 2 | 8 | 183 | 64 | 0 | 0 | 23,3 | 0,672 | 32 | 1 |
| 3 | 1 | 89 | 66 | 23 | 94 | 28,1 | 0,167 | 21 год | 0 |
| 4 | 0 | 137 | 40 | 35 год | 168 | 43,1 | 2,288 | 33 | 1 |
patient_data = data.iloc[:, 3:5].values
import scipy.cluster.hierarchy as shc
plt.figure(figsize=(10, 7))
plt.title("Patient Dendograms")
dend = shc.dendrogram(shc.linkage(data, method='ward'))
from sklearn.cluster import AgglomerativeClustering
cluster = AgglomerativeClustering(n_clusters=4, affinity='euclidean', linkage='ward')
cluster.fit_predict(patient_data)
plt.figure(figsize=(10, 7))
plt.scatter(patient_data[:,0], patient_data[:,1], c=cluster.labels_, cmap='rainbow')
Введение
Алгоритм K-ближайших соседей (KNN) - это тип контролируемого алгоритма машинного обучения, который может использоваться как для классификации, так и для задач прогнозирования регрессии. Однако он в основном используется для задач прогнозирования классификации в промышленности. Следующие два свойства хорошо определяют KNN:
Lazy learning algorithm - KNN - это алгоритм ленивого обучения, потому что он не имеет специальной фазы обучения и использует все данные для обучения при классификации.
Non-parametric learning algorithm - KNN также является непараметрическим алгоритмом обучения, потому что он ничего не предполагает о базовых данных.
Работа алгоритма KNN
Алгоритм K-ближайших соседей (KNN) использует «сходство признаков» для прогнозирования значений новых точек данных, что дополнительно означает, что новой точке данных будет присвоено значение в зависимости от того, насколько близко она соответствует точкам в обучающем наборе. Мы можем понять его работу с помощью следующих шагов -
Step1- Для реализации любого алгоритма нужен набор данных. Итак, на первом этапе KNN мы должны загрузить как обучающие, так и тестовые данные.
Step2- Далее нам нужно выбрать значение K, то есть ближайшие точки данных. K может быть любым целым числом.
Step3 - Для каждой точки в тестовых данных сделайте следующее -
3.1- Рассчитайте расстояние между тестовыми данными и каждой строкой обучающих данных с помощью любого метода, а именно: Евклидова, Манхэттенского или Хэммингового расстояния. Наиболее часто используемый метод расчета расстояния - евклидов.
3.2 - Теперь, исходя из значения расстояния, отсортируйте их в порядке возрастания.
3.3 - Затем он выберет верхние K строк из отсортированного массива.
3.4 - Теперь он назначит класс контрольной точке на основе наиболее частого класса этих строк.
Step4 - Конец
пример
Ниже приведен пример для понимания концепции K и работы алгоритма KNN.
Предположим, у нас есть набор данных, который можно построить следующим образом:
Теперь нам нужно классифицировать новую точку данных с черной точкой (в точке 60,60) на синий или красный класс. Мы предполагаем, что K = 3, т.е. он найдет три ближайших точки данных. Это показано на следующей диаграмме -

На приведенной выше диаграмме мы видим трех ближайших соседей точки данных, отмеченных черной точкой. Среди этих трех два из них относятся к красному классу, поэтому черная точка также будет присвоена красному классу.
Реализация на Python
Как мы знаем, алгоритм K-ближайших соседей (KNN) может использоваться как для классификации, так и для регрессии. Ниже приведены рецепты в Python для использования KNN в качестве классификатора, а также регрессора.
KNN как классификатор
Сначала начнем с импорта необходимых пакетов Python -
import numpy as np
import matplotlib.pyplot as plt
import pandas as pdЗатем загрузите набор данных iris по его веб-ссылке следующим образом:
path = "https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data"Затем нам нужно назначить имена столбцов набору данных следующим образом:
headernames = ['sepal-length', 'sepal-width', 'petal-length', 'petal-width', 'Class']Теперь нам нужно прочитать набор данных в фреймворке pandas следующим образом:
dataset = pd.read_csv(path, names=headernames)
dataset.head()| слно. | длина чашелистика | ширина чашелистика | длина лепестка | ширина лепестка | Класс |
|---|---|---|---|---|---|
| 0 | 5.1 | 3.5 | 1.4 | 0,2 | Ирис-сетоса |
| 1 | 4.9 | 3.0 | 1.4 | 0,2 | Ирис-сетоса |
| 2 | 4,7 | 3.2 | 1.3 | 0,2 | Ирис-сетоса |
| 3 | 4.6 | 3.1 | 1.5 | 0,2 | Ирис-сетоса |
| 4 | 5.0 | 3,6 | 1.4 | 0,2 | Ирис-сетоса |
Предварительная обработка данных будет выполняться с помощью следующих строк скрипта -
X = dataset.iloc[:, :-1].values
y = dataset.iloc[:, 4].valuesДалее мы разделим данные на тренировочную и тестовую. Следующий код разделит набор данных на 60% данных обучения и 40% данных тестирования.
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.40)Далее масштабирование данных будет выполнено следующим образом -
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit(X_train)
X_train = scaler.transform(X_train)
X_test = scaler.transform(X_test)Затем обучите модель с помощью класса sklearn KNeighborsClassifier следующим образом:
from sklearn.neighbors import KNeighborsClassifier
classifier = KNeighborsClassifier(n_neighbors=8)
classifier.fit(X_train, y_train)Наконец-то нам нужно сделать прогноз. Это можно сделать с помощью следующего скрипта -
y_pred = classifier.predict(X_test)Затем распечатайте результаты следующим образом -
from sklearn.metrics import classification_report, confusion_matrix, accuracy_score
result = confusion_matrix(y_test, y_pred)
print("Confusion Matrix:")
print(result)
result1 = classification_report(y_test, y_pred)
print("Classification Report:",)
print (result1)
result2 = accuracy_score(y_test,y_pred)
print("Accuracy:",result2)Вывод
Confusion Matrix:
[[21 0 0]
[ 0 16 0]
[ 0 7 16]]
Classification Report:
precision recall f1-score support
Iris-setosa 1.00 1.00 1.00 21
Iris-versicolor 0.70 1.00 0.82 16
Iris-virginica 1.00 0.70 0.82 23
micro avg 0.88 0.88 0.88 60
macro avg 0.90 0.90 0.88 60
weighted avg 0.92 0.88 0.88 60
Accuracy: 0.8833333333333333KNN как Регрессор
Сначала начнем с импорта необходимых пакетов Python -
import numpy as np
import pandas as pdЗатем загрузите набор данных iris по его веб-ссылке следующим образом:
path = "https://archive.ics.uci.edu/ml/machine-learning-databases/iris/iris.data"Затем нам нужно назначить имена столбцов набору данных следующим образом:
headernames = ['sepal-length', 'sepal-width', 'petal-length', 'petal-width', 'Class']Теперь нам нужно прочитать набор данных в фреймворке pandas следующим образом:
data = pd.read_csv(url, names=headernames)
array = data.values
X = array[:,:2]
Y = array[:,2]
data.shape
output:(150, 5)Затем импортируйте KNeighborsRegressor из sklearn, чтобы соответствовать модели -
from sklearn.neighbors import KNeighborsRegressor
knnr = KNeighborsRegressor(n_neighbors=10)
knnr.fit(X, y)Наконец, мы можем найти MSE следующим образом -
print ("The MSE is:",format(np.power(y-knnr.predict(X),2).mean()))Вывод
The MSE is: 0.12226666666666669Плюсы и минусы KNN
Плюсы
Это очень простой алгоритм для понимания и интерпретации.
Это очень полезно для нелинейных данных, потому что в этом алгоритме нет предположений о данных.
Это универсальный алгоритм, поскольку мы можем использовать его как для классификации, так и для регрессии.
Он имеет относительно высокую точность, но существуют модели обучения с учителем лучше, чем KNN.
Минусы
Это немного дорогостоящий алгоритм с вычислительной точки зрения, потому что он хранит все данные обучения.
Требуется большой объем памяти по сравнению с другими алгоритмами контролируемого обучения.
Прогнозирование медленное в случае большого N.
Он очень чувствителен к масштабу данных, а также к нерелевантным функциям.
Приложения KNN
Ниже приведены некоторые из областей, в которых KNN может успешно применяться:
Банковская система
KNN можно использовать в банковской системе для прогнозирования того, подходит ли физическое лицо для утверждения кредита? Имеет ли этот человек характеристики, аналогичные характеристикам неплательщика?
Расчет кредитных рейтингов
Алгоритмы KNN могут использоваться для определения кредитного рейтинга человека путем сравнения с людьми, имеющими аналогичные черты характера.
Политика
С помощью алгоритмов KNN мы можем разделить потенциального избирателя на различные классы, такие как «проголосует», «не проголосует», «проголосует за съезд партии», «проголосует за партию« BJP ».
Другие области, в которых может использоваться алгоритм KNN, - это распознавание речи, обнаружение рукописного ввода, распознавание изображений и распознавание видео.
Существуют различные метрики, которые мы можем использовать для оценки производительности алгоритмов машинного обучения, классификации, а также алгоритмов регрессии. Мы должны тщательно выбирать метрики для оценки эффективности машинного обучения, потому что:
Способ измерения и сравнения производительности алгоритмов машинного обучения будет полностью зависеть от выбранной вами метрики.
То, как вы оцениваете важность различных характеристик в результате, будет полностью зависеть от выбранной вами метрики.
Метрики производительности для задач классификации
Мы обсуждали классификацию и ее алгоритмы в предыдущих главах. Здесь мы собираемся обсудить различные метрики производительности, которые можно использовать для оценки прогнозов для задач классификации.
Матрица путаницы
Это самый простой способ измерить производительность задачи классификации, когда выходные данные могут относиться к классам двух или более типов. Матрица путаницы - это не что иное, как таблица с двумя измерениями, а именно. «Фактический» и «Прогнозируемый» и, кроме того, оба измерения имеют «Истинные положительные результаты (TP)», «Истинные отрицательные результаты (TN)», «Ложные положительные результаты (FP)», «Ложные отрицательные результаты (FN)», как показано ниже -

Объяснение терминов, связанных с матрицей путаницы, следующее:
True Positives (TP) - Это тот случай, когда и фактический класс, и прогнозируемый класс точки данных равны 1.
True Negatives (TN) - Это тот случай, когда как фактический, так и прогнозируемый класс точки данных равны 0.
False Positives (FP) - Это тот случай, когда фактический класс точки данных равен 0, а прогнозируемый класс точки данных равен 1.
False Negatives (FN) - Это тот случай, когда фактический класс точки данных равен 1, а прогнозируемый класс точки данных равен 0.
Мы можем использовать функцию confusion_matrix из sklearn.metrics для вычисления матрицы путаницы нашей модели классификации.
Точность классификации
Это наиболее распространенный показатель производительности алгоритмов классификации. Его можно определить как количество сделанных правильных прогнозов как отношение ко всем сделанным прогнозам. Мы можем легко вычислить его по матрице путаницы с помощью следующей формулы -
$Accuracy =\frac{TP+TN}{+++}$Мы можем использовать функцию precision_score из sklearn.metrics для вычисления точности нашей модели классификации.
Отчет о классификации
Этот отчет состоит из оценок «Точность», «Отзыв», «F1» и «Поддержка». Они объясняются следующим образом -
Точность
Точность, используемая при поиске документов, может быть определена как количество правильных документов, возвращаемых нашей моделью машинного обучения. Мы можем легко вычислить его по матрице путаницы с помощью следующей формулы -
$Precision=\frac{TP}{TP+FP}$Отзыв или чувствительность
Отзыв можно определить как количество положительных результатов, возвращаемых нашей моделью машинного обучения. Мы можем легко вычислить его по матрице путаницы с помощью следующей формулы -
$Recall =\frac{TP}{TP+FN}$Специфика
Специфичность, в отличие от отзыва, может быть определена как количество негативов, возвращаемых нашей моделью машинного обучения. Мы можем легко вычислить его по матрице путаницы с помощью следующей формулы -
$Specificity =\frac{TN}{TN+FP}$Служба поддержки
Поддержка может быть определена как количество выборок истинного ответа, который лежит в каждом классе целевых значений.
Оценка F1
Эта оценка даст нам гармоническое среднее значение точности и запоминания. Математически оценка F1 представляет собой средневзвешенное значение точности и отзывчивости. Лучшее значение F1 будет равно 1, а худшее - 0. Мы можем рассчитать оценку F1 с помощью следующей формулы:
= * (*) / (+)
Оценка F1 имеет равный относительный вклад точности и запоминания.
Мы можем использовать функцию classification_report из sklearn.metrics, чтобы получить отчет о классификации нашей модели классификации.
AUC (площадь под кривой ROC)
AUC (площадь под кривой) -ROC (рабочая характеристика приемника) - это показатель производительности, основанный на различных пороговых значениях, для проблем классификации. Как следует из названия, ROC представляет собой кривую вероятности, а AUC измеряет разделимость. Проще говоря, метрика AUC-ROC расскажет нам о способности модели различать классы. Чем выше AUC, тем лучше модель.
Математически это может быть создано путем построения графика TPR (истинно положительной скорости), т. Е. Чувствительности или отзыва, против FPR (ложноположительной скорости), т.е. 1-специфичности, при различных пороговых значениях. Ниже приведен график, показывающий ROC, AUC, имеющую TPR по оси y и FPR по оси x.

Мы можем использовать функцию roc_auc_score из sklearn.metrics для вычисления AUC-ROC.
LOGLOSS (логарифмическая потеря)
Это также называется потерей логистической регрессии или перекрестной энтропией. Он в основном определяется на основе оценок вероятности и измеряет эффективность модели классификации, где входными данными является значение вероятности от 0 до 1. Его можно понять более четко, если дифференцировать его с точностью. Поскольку мы знаем, что точность - это количество прогнозов (прогнозируемое значение = фактическое значение) в нашей модели, тогда как Log Loss - это степень неопределенности нашего прогноза, основанная на том, насколько она отличается от фактического значения. С помощью значения Log Loss мы можем получить более точное представление о производительности нашей модели. Мы можем использовать функцию log_loss из sklearn.metrics для вычисления потерь журнала.
пример
Ниже приведен простой рецепт на Python, который даст нам представление о том, как мы можем использовать описанные выше метрики производительности в модели двоичной классификации.
from sklearn.metrics import confusion_matrix
from sklearn.metrics import accuracy_score
from sklearn.metrics import classification_report
from sklearn.metrics import roc_auc_score
from sklearn.metrics import log_loss
X_actual = [1, 1, 0, 1, 0, 0, 1, 0, 0, 0]
Y_predic = [1, 0, 1, 1, 1, 0, 1, 1, 0, 0]
results = confusion_matrix(X_actual, Y_predic)
print ('Confusion Matrix :')
print(results)
print ('Accuracy Score is',accuracy_score(X_actual, Y_predic))
print ('Classification Report : ')
print (classification_report(X_actual, Y_predic))
print('AUC-ROC:',roc_auc_score(X_actual, Y_predic))
print('LOGLOSS Value is',log_loss(X_actual, Y_predic))Вывод
Confusion Matrix :
[[3 3]
[1 3]]
Accuracy Score is 0.6
Classification Report :
precision recall f1-score support
0 0.75 0.50 0.60 6
1 0.50 0.75 0.60 4
micro avg 0.60 0.60 0.60 10
macro avg 0.62 0.62 0.60 10
weighted avg 0.65 0.60 0.60 10
AUC-ROC: 0.625
LOGLOSS Value is 13.815750437193334Метрики производительности для задач регрессии
Мы обсуждали регрессию и ее алгоритмы в предыдущих главах. Здесь мы собираемся обсудить различные метрики производительности, которые можно использовать для оценки прогнозов для проблем регрессии.
Средняя абсолютная ошибка (MAE)
Это простейшая метрика ошибок, используемая в задачах регрессии. По сути, это сумма среднего значения абсолютной разницы между прогнозируемыми и фактическими значениями. Проще говоря, с помощью MAE мы можем понять, насколько ошибочными были прогнозы. MAE не указывает направление модели, т. Е. Никаких указаний на недостаточную или избыточную производительность модели. Ниже приводится формула для расчета MAE -
$MAE = \frac{1}{n}\sum|Y -\hat{Y}|$Здесь = Фактические выходные значения
И $\hat{Y}$= Прогнозируемые выходные значения.
Мы можем использовать функцию mean_absolute_error из sklearn.metrics для вычисления MAE.
Среднеквадратичная ошибка (MSE)
MSE похожа на MAE, но с той лишь разницей, что она возводит в квадрат разность фактических и прогнозируемых выходных значений перед их суммированием вместо использования абсолютного значения. Разницу можно заметить в следующем уравнении -
$MSE = \frac{1}{n}\sum(Y -\hat{Y})$Здесь = Фактические выходные значения
И $\hat{Y}$ = Прогнозируемые выходные значения.
Мы можем использовать функцию mean_squared_error из sklearn.metrics для вычисления MSE.
R в квадрате (R 2 )
Показатель R в квадрате обычно используется для пояснительных целей и обеспечивает указание соответствия или соответствия набора прогнозируемых выходных значений фактическим выходным значениям. Следующая формула поможет нам понять это -
$R^{2} = 1 -\frac{\frac{1}{n}\sum_{i{=1}}^n(Y_{i}-\hat{Y_{i}})^2}{\frac{1}{n}\sum_{i{=1}}^n(Y_{i}-\bar{Y_i)^2}}$В приведенном выше уравнении числитель - это MSE, а знаменатель - это дисперсия значений.
Мы можем использовать функцию r2_score из sklearn.metrics для вычисления значения R.
пример
Ниже приведен простой рецепт на Python, который даст нам представление о том, как мы можем использовать описанные выше метрики производительности в регрессионной модели.
from sklearn.metrics import r2_score
from sklearn.metrics import mean_absolute_error
from sklearn.metrics import mean_squared_error
X_actual = [5, -1, 2, 10]
Y_predic = [3.5, -0.9, 2, 9.9]
print ('R Squared =',r2_score(X_actual, Y_predic))
print ('MAE =',mean_absolute_error(X_actual, Y_predic))
print ('MSE =',mean_squared_error(X_actual, Y_predic))Вывод
R Squared = 0.9656060606060606
MAE = 0.42499999999999993
MSE = 0.5674999999999999Введение
Для успешного выполнения и получения результатов модель машинного обучения должна автоматизировать некоторые стандартные рабочие процессы. Процесс автоматизации этих стандартных рабочих процессов может быть выполнен с помощью Scikit-learn Pipelines. С точки зрения специалистов по данным, конвейер - это обобщенное, но очень важное понятие. Это в основном позволяет передавать данные из необработанного формата в некоторую полезную информацию. Работу трубопроводов можно понять с помощью следующей схемы -

Блоки трубопроводов ML следующие:
Data ingestion- Как следует из названия, это процесс импорта данных для использования в проекте ML. Данные можно извлекать в режиме реального времени или партиями из одной или нескольких систем. Это один из самых сложных шагов, поскольку качество данных может повлиять на всю модель машинного обучения.
Data Preparation- После импорта данных нам нужно подготовить данные для использования в нашей модели машинного обучения. Предварительная обработка данных - один из важнейших методов подготовки данных.
ML Model Training- Следующим шагом будет обучение нашей модели машинного обучения. У нас есть различные алгоритмы машинного обучения, такие как контролируемые, неконтролируемые, подкрепляющие, чтобы извлекать функции из данных и делать прогнозы.
Model Evaluation- Далее нам нужно оценить модель машинного обучения. В случае конвейера AutoML модель ML может быть оценена с помощью различных статистических методов и бизнес-правил.
ML Model retraining- В случае конвейера AutoML не обязательно, чтобы первая модель была лучшей. Первая модель считается базовой, и мы можем обучать ее многократно, чтобы повысить точность модели.
Deployment- Наконец-то нам нужно развернуть модель. Этот шаг включает применение и перенос модели в бизнес-операции для их использования.
Проблемы, связанные с конвейерами машинного обучения
При создании конвейеров машинного обучения специалисты по обработке данных сталкиваются с множеством проблем. Эти проблемы делятся на следующие три категории:
Качество данных
Успех любой модели машинного обучения во многом зависит от качества данных. Если данные, которые мы предоставляем модели машинного обучения, неточны, надежны и надежны, то мы собираемся закончить с неправильным или вводящим в заблуждение результатом.
Надежность данных
Еще одна проблема, связанная с конвейерами машинного обучения, - это надежность данных, которые мы предоставляем модели машинного обучения. Как мы знаем, могут быть различные источники, из которых специалист по данным может получать данные, но для получения наилучших результатов необходимо быть уверенным, что источники данных надежны и заслуживают доверия.
Доступность данных
Чтобы получить наилучшие результаты от конвейеров машинного обучения, должны быть доступны сами данные, что требует консолидации, очистки и обработки данных. В результате свойства доступности данных метаданные будут обновлены новыми тегами.
Моделирование конвейера машинного обучения и подготовка данных
Утечка данных, происходящая из набора обучающих данных в набор данных тестирования, является важной проблемой, с которой специалист по данным может столкнуться при подготовке данных для модели машинного обучения. Как правило, во время подготовки данных специалист по данным перед обучением использует такие методы, как стандартизация или нормализация для всего набора данных. Но эти методы не могут помочь нам от утечки данных, потому что на набор обучающих данных повлиял бы масштаб данных в наборе данных тестирования.
Используя конвейеры машинного обучения, мы можем предотвратить эту утечку данных, поскольку конвейеры гарантируют, что подготовка данных, такая как стандартизация, ограничивается каждым этапом нашей процедуры перекрестной проверки.
пример
Ниже приведен пример на Python, демонстрирующий рабочий процесс подготовки данных и оценки модели. Для этой цели мы используем набор данных Pima Indian Diabetes от Sklearn. Сначала мы создадим конвейер, стандартизирующий данные. Затем будет создана модель линейного дискриминативного анализа, и, наконец, конвейер будет оценен с использованием 10-кратной перекрестной проверки.
Сначала импортируйте необходимые пакеты следующим образом:
from pandas import read_csv
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import Pipeline
from sklearn.discriminant_analysis import LinearDiscriminantAnalysisТеперь нам нужно загрузить набор данных о диабете Pima, как это было в предыдущих примерах -
path = r"C:\pima-indians-diabetes.csv"
headernames = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=headernames)
array = data.valuesЗатем мы создадим конвейер с помощью следующего кода -
estimators = []
estimators.append(('standardize', StandardScaler()))
estimators.append(('lda', LinearDiscriminantAnalysis()))
model = Pipeline(estimators)Наконец, мы собираемся оценить этот конвейер и вывести его точность следующим образом:
kfold = KFold(n_splits=20, random_state=7)
results = cross_val_score(model, X, Y, cv=kfold)
print(results.mean())Вывод
0.7790148448043184Приведенный выше вывод представляет собой сводку точности настройки набора данных.
Моделирование конвейера машинного обучения и извлечения признаков
Утечка данных также может произойти на этапе извлечения признаков модели ML. Вот почему процедуры извлечения признаков также должны быть ограничены, чтобы остановить утечку данных в нашем наборе обучающих данных. Как и в случае с подготовкой данных, с помощью конвейеров машинного обучения мы можем предотвратить утечку данных. Для этой цели можно использовать FeatureUnion, инструмент, предоставляемый конвейерами машинного обучения.
пример
Ниже приведен пример на Python, демонстрирующий рабочий процесс извлечения признаков и оценки модели. Для этой цели мы используем набор данных Pima Indian Diabetes от Sklearn.
Во-первых, 3 функции будут извлечены с помощью PCA (анализа главных компонентов). Затем 6 объектов будут извлечены с помощью статистического анализа. После извлечения признаков результат нескольких процедур выбора и извлечения будет объединен с помощью
Инструмент FeatureUnion. Наконец, будет создана модель логистической регрессии, и конвейер будет оценен с использованием 10-кратной перекрестной проверки.
Сначала импортируйте необходимые пакеты следующим образом:
from pandas import read_csv
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.pipeline import Pipeline
from sklearn.pipeline import FeatureUnion
from sklearn.linear_model import LogisticRegression
from sklearn.decomposition import PCA
from sklearn.feature_selection import SelectKBestТеперь нам нужно загрузить набор данных о диабете Pima, как это было в предыдущих примерах -
path = r"C:\pima-indians-diabetes.csv"
headernames = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=headernames)
array = data.valuesЗатем объединение функций будет создано следующим образом -
features = []
features.append(('pca', PCA(n_components=3)))
features.append(('select_best', SelectKBest(k=6)))
feature_union = FeatureUnion(features)Далее конвейер будет создан с помощью следующих строк скрипта -
estimators = []
estimators.append(('feature_union', feature_union))
estimators.append(('logistic', LogisticRegression()))
model = Pipeline(estimators)Наконец, мы собираемся оценить этот конвейер и вывести его точность следующим образом:
kfold = KFold(n_splits=20, random_state=7)
results = cross_val_score(model, X, Y, cv=kfold)
print(results.mean())Вывод
0.7789811066126855Приведенный выше вывод представляет собой сводку точности настройки набора данных.
Повышение производительности с помощью ансамблей
Ансамбли могут улучшить результат машинного обучения, комбинируя несколько моделей. По сути, ансамблевые модели состоят из нескольких индивидуально обученных моделей обучения с учителем, и их результаты объединяются различными способами для достижения более высоких показателей прогнозирования по сравнению с одной моделью. Ансамблевые методы можно разделить на следующие две группы:
Последовательные ансамблевые методы
Как следует из названия, в таких методах ансамбля базовые учащиеся генерируются последовательно. Мотивация таких методов заключается в использовании зависимости между базовыми учащимися.
Параллельные ансамблевые методы
Как следует из названия, в таких методах ансамбля базовые учащиеся генерируются параллельно. Мотивация таких методов - использовать независимость базовых учеников.
Методы ансамблевого обучения
Ниже приведены наиболее популярные методы ансамблевого обучения, то есть методы комбинирования прогнозов из разных моделей.
Упаковка
Термин пакетирование также известен как агрегирование начальной загрузки. В методах упаковки модель ансамбля пытается повысить точность прогнозирования и уменьшить дисперсию модели путем объединения прогнозов отдельных моделей, обученных на случайно сгенерированных обучающих выборках. Окончательный прогноз ансамблевой модели будет дан путем вычисления среднего значения всех прогнозов отдельных оценщиков. Один из лучших примеров использования мешков - случайные леса.
Повышение
В методе повышения главный принцип построения ансамблевой модели состоит в том, чтобы строить ее постепенно, последовательно обучая каждый оценщик базовой модели. Как следует из названия, он в основном объединяет нескольких недельных базовых учеников, обучаемых последовательно на нескольких итерациях обучающих данных, для создания мощного ансамбля. Во время обучения недельных базовых учеников более высокие веса назначаются тем ученикам, которые ранее были неправильно классифицированы. Пример метода повышения - AdaBoost.
Голосование
В этой модели ансамблевого обучения построено несколько моделей разных типов, и для комбинирования прогнозов используются некоторые простые статистические данные, такие как вычисление среднего или медианного значения и т. Д. Этот прогноз будет служить дополнительным входом для обучения, чтобы сделать окончательный прогноз.
Алгоритмы ансамбля мешков
Ниже приведены три алгоритма ансамбля упаковки:
Упакованное дерево решений
Как мы знаем, методы ансамбля пакетов хорошо работают с алгоритмами, имеющими высокую дисперсию, и в этом отношении лучшим из них является алгоритм дерева решений. В следующем рецепте Python мы собираемся построить модель ансамбля дерева решений с пакетом решений, используя функцию sklearn BaggingClassifier с DecisionTreeClasifier (алгоритм деревьев классификации и регрессии) на наборе данных о диабете индейцев пима.
Сначала импортируйте необходимые пакеты следующим образом:
from pandas import read_csv
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.ensemble import BaggingClassifier
from sklearn.tree import DecisionTreeClassifierТеперь нам нужно загрузить набор данных о диабете Pima, как мы это делали в предыдущих примерах -
path = r"C:\pima-indians-diabetes.csv"
headernames = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=headernames)
array = data.values
X = array[:,0:8]
Y = array[:,8]Затем введите данные для 10-кратной перекрестной проверки следующим образом:
seed = 7
kfold = KFold(n_splits=10, random_state=seed)
cart = DecisionTreeClassifier()Нам нужно указать количество деревьев, которые мы собираемся построить. Вот 150 деревьев строим -
num_trees = 150Затем создайте модель с помощью следующего скрипта -
model = BaggingClassifier(base_estimator=cart, n_estimators=num_trees, random_state=seed)Рассчитайте и распечатайте результат следующим образом -
results = cross_val_score(model, X, Y, cv=kfold)
print(results.mean())Вывод
0.7733766233766234Приведенный выше результат показывает, что мы получили около 77% точности нашей модели классификатора дерева решений.
Случайный лес
Это расширение деревьев решений в мешках. Для отдельных классификаторов выборки обучающего набора данных берутся с заменой, но деревья строятся таким образом, чтобы уменьшить корреляцию между ними. Кроме того, считается, что случайный набор функций выбирает каждую точку разделения, а не жадно выбирает лучшую точку разделения при построении каждого дерева.
В следующем рецепте Python мы собираемся построить модель ансамбля случайных лесов в мешках с использованием класса sklearn RandomForestClassifier в наборе данных о диабете индейцев пима.
Сначала импортируйте необходимые пакеты следующим образом:
from pandas import read_csv
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.ensemble import RandomForestClassifierТеперь нам нужно загрузить набор данных о диабете Pima, как это было в предыдущих примерах -
path = r"C:\pima-indians-diabetes.csv"
headernames = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=headernames)
array = data.values
X = array[:,0:8]
Y = array[:,8]Затем введите данные для 10-кратной перекрестной проверки следующим образом:
seed = 7
kfold = KFold(n_splits=10, random_state=seed)Нам нужно указать количество деревьев, которые мы собираемся построить. Здесь мы строим 150 деревьев с точками разделения, выбранными из 5 функций:
num_trees = 150
max_features = 5Затем создайте модель с помощью следующего скрипта -
model = RandomForestClassifier(n_estimators=num_trees, max_features=max_features)Рассчитайте и распечатайте результат следующим образом -
results = cross_val_score(model, X, Y, cv=kfold)
print(results.mean())Вывод
0.7629357484620642Приведенные выше выходные данные показывают, что мы получили около 76% точности нашей модели классификатора случайных лесов.
Дополнительные деревья
Это еще одно расширение метода ансамбля деревьев решений с мешками. В этом методе случайные деревья строятся из выборок обучающего набора данных.
В следующем рецепте Python мы собираемся построить дополнительную модель ансамбля деревьев, используя класс Sklearn ExtraTreesClassifier в наборе данных о диабете индейцев пима.
Сначала импортируйте необходимые пакеты следующим образом:
from pandas import read_csv
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.ensemble import ExtraTreesClassifierТеперь нам нужно загрузить набор данных о диабете Pima, как это было в предыдущих примерах -
path = r"C:\pima-indians-diabetes.csv"
headernames = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=headernames)
array = data.values
X = array[:,0:8]
Y = array[:,8]Затем введите данные для 10-кратной перекрестной проверки следующим образом:
seed = 7
kfold = KFold(n_splits=10, random_state=seed)Нам нужно указать количество деревьев, которые мы собираемся построить. Здесь мы строим 150 деревьев с точками разделения, выбранными из 5 функций:
num_trees = 150
max_features = 5Затем создайте модель с помощью следующего скрипта -
model = ExtraTreesClassifier(n_estimators=num_trees, max_features=max_features)Рассчитайте и распечатайте результат следующим образом -
results = cross_val_score(model, X, Y, cv=kfold)
print(results.mean())Вывод
0.7551435406698566Приведенный выше результат показывает, что мы получили около 75,5% точности нашей модели классификатора дополнительных деревьев в мешках.
Повышение ансамблевых алгоритмов
Ниже приведены два наиболее распространенных алгоритма ансамбля повышения:
AdaBoost
Это один из наиболее успешных алгоритмов ансамбля повышения. Главный ключ этого алгоритма - то, как они присваивают веса экземплярам в наборе данных. По этой причине алгоритм должен уделять меньше внимания экземплярам при построении последующих моделей.
В следующем рецепте Python мы собираемся построить модель ансамбля Ada Boost для классификации с использованием класса Sklearn AdaBoostClassifier в наборе данных о диабете индейцев пима.
Сначала импортируйте необходимые пакеты следующим образом:
from pandas import read_csv
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.ensemble import AdaBoostClassifierТеперь нам нужно загрузить набор данных о диабете Pima, как это было в предыдущих примерах -
path = r"C:\pima-indians-diabetes.csv"
headernames = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=headernames)
array = data.values
X = array[:,0:8]
Y = array[:,8]Затем введите данные для 10-кратной перекрестной проверки следующим образом:
seed = 5
kfold = KFold(n_splits=10, random_state=seed)Нам нужно указать количество деревьев, которые мы собираемся построить. Здесь мы строим 150 деревьев с точками разделения, выбранными из 5 функций:
num_trees = 50Затем создайте модель с помощью следующего скрипта -
model = AdaBoostClassifier(n_estimators=num_trees, random_state=seed)Рассчитайте и распечатайте результат следующим образом -
results = cross_val_score(model, X, Y, cv=kfold)
print(results.mean())Вывод
0.7539473684210527Приведенный выше результат показывает, что мы получили около 75% точности нашей модели ансамбля классификатора AdaBoost.
Стохастическое повышение градиента
Его также называют машинами для повышения градиента. В следующем рецепте Python мы собираемся построить модель Stochastic Gradient Boostingensemble для классификации с использованием класса Sklearn GradientBoostingClassifier на наборе данных о диабете индейцев пима.
Сначала импортируйте необходимые пакеты следующим образом:
from pandas import read_csv
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.ensemble import GradientBoostingClassifierТеперь нам нужно загрузить набор данных о диабете Pima, как это было в предыдущих примерах -
path = r"C:\pima-indians-diabetes.csv"
headernames = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=headernames)
array = data.values
X = array[:,0:8]
Y = array[:,8]Затем введите данные для 10-кратной перекрестной проверки следующим образом:
seed = 5
kfold = KFold(n_splits=10, random_state=seed)Нам нужно указать количество деревьев, которые мы собираемся построить. Здесь мы строим 150 деревьев с точками разделения, выбранными из 5 функций:
num_trees = 50Затем создайте модель с помощью следующего скрипта -
model = GradientBoostingClassifier(n_estimators=num_trees, random_state=seed)Рассчитайте и распечатайте результат следующим образом -
results = cross_val_score(model, X, Y, cv=kfold)
print(results.mean())Вывод
0.7746582365003418Приведенный выше результат показывает, что точность нашей модели классификатора Gradient Boosting составляет около 77,5%.
Алгоритмы ансамбля голосования
Как уже говорилось, голосование сначала создает две или более автономных моделей из набора обучающих данных, а затем классификатор голосования обертывает модель вместе с усреднением прогнозов подмодели всякий раз, когда требуются новые данные.
В следующем рецепте Python мы собираемся построить модель ансамбля голосования для классификации с использованием класса sklearn VotingClassifier в наборе данных о диабете индейцев пима. Мы объединяем прогнозы логистической регрессии, классификатора дерева решений и SVM вместе для задачи классификации следующим образом:
Сначала импортируйте необходимые пакеты следующим образом:
from pandas import read_csv
from sklearn.model_selection import KFold
from sklearn.model_selection import cross_val_score
from sklearn.linear_model import LogisticRegression
from sklearn.tree import DecisionTreeClassifier
from sklearn.svm import SVC
from sklearn.ensemble import VotingClassifierТеперь нам нужно загрузить набор данных о диабете Pima, как это было в предыдущих примерах -
path = r"C:\pima-indians-diabetes.csv"
headernames = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=headernames)
array = data.values
X = array[:,0:8]
Y = array[:,8]Затем введите данные для 10-кратной перекрестной проверки следующим образом:
kfold = KFold(n_splits=10, random_state=7)Затем нам нужно создать подмодели следующим образом:
estimators = []
model1 = LogisticRegression()
estimators.append(('logistic', model1))
model2 = DecisionTreeClassifier()
estimators.append(('cart', model2))
model3 = SVC()
estimators.append(('svm', model3))Теперь создайте модель ансамбля голосования, объединив прогнозы созданных выше подмоделей.
ensemble = VotingClassifier(estimators)
results = cross_val_score(ensemble, X, Y, cv=kfold)
print(results.mean())Вывод
0.7382262474367738Приведенный выше результат показывает, что точность нашей модели ансамбля классификаторов голосования составляет около 74%.
Повышение производительности за счет настройки алгоритма
Как мы знаем, модели машинного обучения параметризованы таким образом, что их поведение можно адаптировать для конкретной проблемы. Настройка алгоритма означает поиск наилучшей комбинации этих параметров, чтобы можно было улучшить производительность модели машинного обучения. Этот процесс иногда называют гиперпараметрической оптимизацией, а параметры самого алгоритма называют гиперпараметрами, а коэффициенты, найденные алгоритмом ML, называют параметрами.
Здесь мы собираемся обсудить некоторые методы настройки параметров алгоритма, предоставляемые Python Scikit-learn.
Настройка параметров поиска по сетке
Это подход к настройке параметров. Ключевым моментом работы этого метода является то, что он строит и методически оценивает модель для всех возможных комбинаций параметров алгоритма, указанных в сетке. Следовательно, можно сказать, что этот алгоритм носит поисковый характер.
пример
В следующем рецепте Python мы собираемся выполнить поиск по сетке с использованием класса sklearn GridSearchCV для оценки различных альфа-значений для алгоритма регрессии хребта в наборе данных о диабете индейцев пима.
Сначала импортируйте необходимые пакеты следующим образом:
import numpy
from pandas import read_csv
from sklearn.linear_model import Ridge
from sklearn.model_selection import GridSearchCVТеперь нам нужно загрузить набор данных о диабете Pima, как это было в предыдущих примерах -
path = r"C:\pima-indians-diabetes.csv"
headernames = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=headernames)
array = data.values
X = array[:,0:8]
Y = array[:,8]Затем оцените различные значения альфа следующим образом:
alphas = numpy.array([1,0.1,0.01,0.001,0.0001,0])
param_grid = dict(alpha=alphas)Теперь нам нужно применить поиск по сетке к нашей модели -
model = Ridge()
grid = GridSearchCV(estimator=model, param_grid=param_grid)
grid.fit(X, Y)Распечатайте результат со следующей строкой скрипта -
print(grid.best_score_)
print(grid.best_estimator_.alpha)Вывод
0.2796175593129722
1.0Приведенный выше результат дает нам оптимальную оценку и набор параметров в сетке, которые достигли этой оценки. Альфа-значение в данном случае равно 1.0.
Настройка параметров случайного поиска
Это подход к настройке параметров. Ключевым моментом работы этого метода является то, что он производит выборку параметров алгоритма из случайного распределения для фиксированного числа итераций.
пример
В следующем рецепте Python мы собираемся выполнить случайный поиск с использованием класса sklearn RandomizedSearchCV для оценки различных альфа-значений от 0 до 1 для алгоритма Ridge Regression в наборе данных о диабете индейцев пима.
Сначала импортируйте необходимые пакеты следующим образом:
import numpy
from pandas import read_csv
from scipy.stats import uniform
from sklearn.linear_model import Ridge
from sklearn.model_selection import RandomizedSearchCVТеперь нам нужно загрузить набор данных о диабете Pima, как это было в предыдущих примерах -
path = r"C:\pima-indians-diabetes.csv"
headernames = ['preg', 'plas', 'pres', 'skin', 'test', 'mass', 'pedi', 'age', 'class']
data = read_csv(path, names=headernames)
array = data.values
X = array[:,0:8]
Y = array[:,8]Затем оцените различные значения альфа по алгоритму регрессии Риджа следующим образом:
param_grid = {'alpha': uniform()}
model = Ridge()
random_search = RandomizedSearchCV(estimator=model, param_distributions=param_grid, n_iter=50,
random_state=7)
random_search.fit(X, Y)Распечатайте результат со следующей строкой скрипта -
print(random_search.best_score_)
print(random_search.best_estimator_.alpha)Вывод
0.27961712703051084
0.9779895119966027
0.9779895119966027Приведенный выше результат дает нам оптимальную оценку, аналогичную поиску по сетке.